混凝土收縮徐變預測模型試驗研究

韓偉威，呂毅剛

?

混凝土收縮徐變預測模型試驗研究

韓偉威1, 2，呂毅剛3

(1. 長沙理工大學公路養護技術國家工程實驗室，湖南長沙，410114；2. 長沙理工大學交通運輸工程學院，湖南長沙，410114；3. 長沙理工大學橋梁結構安全控制湖南省工程實驗室，湖南長沙，410114)

對長期觀測的混凝土收縮徐變試驗結果與不同規范模型的預測結果進行對比分析。研究結果表明：在恒溫恒濕環境下，收縮徐變在前期發展較快，后期逐漸變緩，270d后變化較小；長期觀測的混凝土收縮徐變試驗結果與不同規范模型的預測結果存在差異，CEB—FIP(1990)模型預測混凝土收縮應變和ACI 209R(1992)模型預測混凝土徐變系數的整體效果較好，而ACI 209R(1992)模型的收縮應變預測值和JTJ 023—85模型的徐變系數預測值與試驗結果偏離較大。根據混凝土收縮徐變試驗結果，引入混凝土收縮修正系數和徐變修正系數對JTG D62—2004預測模型進行修正，構建恒溫恒濕環境下混凝土收縮應變、徐變系數的修正預測模型，提高混凝土收縮徐變預測模型的預測精度。

混凝土；收縮；徐變系數；預測模型；修正系數

混凝土收縮徐變是材料本身特有的時變特性，隨著時間的推移不斷發生變化，嚴重影響混凝土的耐久性能和長期變形性能[1?4]。人類于19世紀認識了混凝土的收縮和徐變，并對其進行了大量研究，但混凝土的收縮徐變機理尚不完善。混凝土收縮徐變會引起結構的內力和變形隨時間不斷變化，若對收縮徐變認識不準，則會導致結構撓度過大，甚至產生裂縫產生。20世紀30年代，國外開始系統地進行混凝土收縮徐變研究，結合數值方法和計算機優化等手段，對大量的試驗結果進行了統計分析，提出和改進了許多混凝土收縮徐變數學預測模型，目前常用的有CEB-FIP系列模型、ACI209系列模型、BS系列模型、B-P系列模型、GZ(1993)模型和GL 2000模型等[5?7]。這些模型考慮的影響因素各有差異，計算精度也不完全相同。我國于20世紀60年代才開始系統地開展混凝土收縮徐變試驗研究[8?20]。曹國輝等[21]對不同加載齡期的素混凝土柱進行了長達600 d的持荷試驗，修正了 CEB—FIP(1990)混凝土徐變預測模型；謝楠等[22]對噴射混凝土的早齡期徐變進行了試驗研究，提出了適合于早齡期噴射混凝土的GL2000修正預測模型；楊健輝等[23]分別對C80和C100高強混凝土進行了28 d收縮和150 d徐變的試驗研究，并對B3模型進行了修正；陳萌等[24]對商品混凝土無筋構件進行了360 d收縮試驗觀測，獲得了商品混凝土的多系數收縮變形預測模型；羅俊禮等[25]對再生骨料高性能混凝土進行了收縮徐變試驗研究，提出了相應的混凝土收縮徐變預測模型。在我國橋涵設計規范中，大都采用了國外的形式，如JTG023—85和JTG D62—2004規范分別采用了CEB?FIP(1978)及CEB?FIP(1990)的表達形式。混凝土收縮徐變及其對結構性能影響的預計和控制十分復雜，難以獲得精確解，基于試驗的經驗或半經驗的混凝土收縮徐變預測模型誤差較大[26?27]。美國混凝土學會209委員會在報告中指出，混凝土收縮徐變特性隨影響因素變化而產生的變異為15%~20%。到目前為止，還沒有一種理論可以準確無誤地解釋或預測混凝土的收縮徐變特性。要正確地分析收縮徐變對混凝土結構使用性能的影響，需選擇能夠反映材料實際情況的收縮徐變數學模式。為此，本文作者開展混凝土收縮徐變試驗研究，構建混凝土收縮徐變預測模型。

1 混凝土收縮徐變試驗概況

共制作5個圓柱形素混凝土柱構件，其中3個構件為混凝土收縮柱，編號分別為SSZ-7，SSZ-7-a和SSZ-7-b；2個構件為混凝土徐變柱，編號分別為SXZ-5和SXZ-6。柱的高度×直徑為600 mm×150 mm，混凝土強度等級為C50混凝土，采用42.5R普通硅酸鹽水泥，水泥、砂、碎石、水、減水劑的質量比為460.00:585.00: 1 175.00:232.50: 3.68。采用千斤頂及壓力傳感器，對徐變架上的徐變柱進行軸心加載，軸向力為159.1 kN，加載齡期0為21 d。在長期試驗過程中，保持軸向力不變。

在所有混凝土柱中埋設振弦式應變傳感器，測試構件的收縮徐變變形，并在表面對稱安裝機械式千分表進行數據復核。試驗裝置加載及測試見圖1。試驗在溫度和相對濕度分別為22.0 ℃和55.0%的恒溫恒濕環境中進行。混凝土長期力學性能測試結果見表1和表2。

數據單位：mm

表1 混凝土抗壓強度

表2 混凝土彈性模量

2 混凝土收縮徐變試驗結果及對比分析

2.1 混凝土收縮試驗結果及對比分析

2.1.1 混凝土收縮試驗結果

在恒溫恒濕環境下，各收縮柱的收縮應變隨時間的變化見圖2(其中，應變以受壓為正；s為收縮開始時的混凝土齡期(d)；為計算齡期(d))。混凝土收縮試驗結果具有以下特點：

1)SSZ-7號柱、SSZ-7-a號柱和SSZ-7-b號柱的收縮應變實測最大值分別為604，560和582；SSZ-7號柱與SSZ-7-a號柱的應變最大值相對誤差為7.86%，SSZ-7號柱與SSZ-7-b號柱應變最大值的相對誤差為3.78%，SSZ-7-a號柱與SSZ-7-b號柱的應變最大值相對誤差為3.93%，均較小。

2) 混凝土的收縮應變實測值在前期發展較快，后期發展較為平緩，270d后變化較小。當干燥持續時間(?s)為30 d時，SSZ-7號柱、SSZ-7-a號柱和SSZ-7-b號柱的收縮應變分別增大至310，259和312；當干燥持續時間(?s)由30 d變化至270 d時，SSZ-7號柱、SSZ-7-a號柱和SSZ-7-b號柱的收縮應變分別增大76.28%，98.74%和70.07%；當干燥持續時間(?s)由270 d變化至768 d時，SSZ-7號柱、SSZ-7-a號柱和SSZ-7-b號柱的收縮應變僅分別增大10.71%，9.05%和9.51%。

1—SSZ-7號柱實測值；2—SSZ-7-a號柱實測值；3—SSZ-7-b號柱實測值。

2.1.2 國內外收縮應變預測模型對比分析

國內外幾種常用模型的收縮應變預測值與實測值隨時間變化的對比見圖3。

(a) SSZ-7號柱；(b) SSZ-7-a號柱；(c) SSZ-7-b號柱1—ACI 209R(1992)；2—GL2000；3—SSZ-7號柱實測值；4—SSZ-7-a號柱實測值；5—SSZ-7-b號柱實測值；6—CEB?FIP(1990)；7—JTG D62—2004；8—JTJ 023—85。

從圖3可以看出：在收縮前期，ACI 209R(1992)和GL2000模型的收縮應變預測值比其他3種模型的預測值更接近于實測值；隨著齡期增長，ACI 209R(1992)和GL2000模型高估了混凝土的收縮應變，而JTG D62—2004，JTJ 023—85和CEB?FIP(1990)模型低估了混凝土的收縮應變，部分研究成果與文獻[16]中的一致；SSZ-7號柱收縮應變實測最大值與JTG D62—2004，JTJ 023—85，CEB?FIP(1990)，ACI 209R(1992)和GL2000等模型的預測值分別相差23.62%，28.48%，15.30%，42.82%和25.63%；SSZ-7-a號柱收縮應變實測最大值與各模型的預測值分別相差17.63%，22.85%，33.49%，54.02%和25.63%；SSZ-7-b號柱收縮應變實測最大值與各模型的預測值分別相差20.67%，25.70%，12.03%，48.33%和30.48%。與試驗結果吻合相對較好的是CEB?FIP(1990)模型，其次為JTG D62—2004模型，而ACI 209R(1992)模型吻合度較低。

2.2 混凝土徐變試驗結果及對比分析

2.2.1 混凝土徐變試驗結果

以0為起始時刻，在恒溫恒濕環境下，各徐變柱的徐變系數隨持荷時間(?0)的變化見圖4。混凝土徐變試驗結果具有以下特點。

混凝土的徐變系數實測值前期發展較快，后期較為平緩，270d后變化較小。但實測的徐變在前期不穩定，存在波動。當持荷時間(?0)為30 d時，SXZ-5號柱和SXZ-6號柱的徐變系數分別為0.969 3和 0.818 4；當持荷時間(?0)由30 d變化至270 d時，SXZ-5號柱和SXZ-6號柱的徐變系數分別增大63.97%和99.54%；當持荷時間(?0)由270 d變化至750 d時，SXZ-5號柱和SXZ-6號柱的徐變系數僅分別增大8.97%和8.55%；當持荷時間(?0)為750 d時，SXZ-5號柱和SXZ-6號柱的徐變系數分別為1.731 9和1.772 6，相對誤差僅為2.35%，兩者試驗結果較吻合。

1—SXZ-5號柱實測值；2—SXZ-6號柱實測值。

2.2.2 國內外徐變系數預測模型對比分析

國內外幾種常用模型的徐變系數預測值與實測值隨時間變化的對比見圖5。從圖5可以看出：

1)各模型的混凝土徐變系數預測值之間差異較大，實測值一般比各模型的預測值低。隨著計算齡期增長，試驗值與不同模型預測值的差異逐漸增大。當持荷時間(?0)為750 d時，SXZ-5號柱的徐變系數與JTG D62—2004，JTJ 023—85，CEB?FIP(1990)，ACI 209R(1992)和GL2000等模型的預測值分別相差38.23%，68.26%，52.92%，6.17%和21.23%；SXZ-6號柱的徐變系數與各模型的預測值分別相差35.06%，64.40%，49.41%，3.73%和18.45%。

2)在各預測模型中，ACI 209R(1992)模型的預測值與試驗結果較吻合，而JTJ 023—85模型的預測結果與試驗結果相差最大。與JTJ 023—85模型相比較，JTG D62—2004模型的預測結果更接近于試驗結果，且從徐變發展趨勢上分析，隨著持荷時間(?0)的增大，JTG D62—2004模型與試驗結果的吻合程度有很大提高。

(a) SXZ-5號柱；(b) SXZ-6號柱1—JTJ 023—85；2—CEB?FIP(1990)；3—JTG D62—2004；4—GL2000；5—ACI 209R(1992)；6—SXZ-5號柱實測值；7—SXZ-6號柱實測值。

3 混凝土收縮徐變修正預測模型

3.1 混凝土收縮應變修正預測模型

在恒溫恒濕環境下，以JTG D62—2004收縮應變預測模型為基礎，設混凝土收縮應變cs(，s)的修正預測模型為

式中：cso和s(t?s)分別為名義收縮系數和收縮隨時間發展的系數，其表達式見文獻[28]；(?s)為混凝土的收縮修正系數。

基于恒溫恒濕環境下的混凝土收縮試驗，混凝土的收縮修正系數(?s)的時變規律模型為

在恒溫恒濕環境下，混凝土的收縮修正系數(?s)的實測值與公式擬合值的時變規律曲線對比見圖6；收縮應變的修正預測模型的預測值與各收縮柱的實測值比較見圖7，可見預測值與實測值吻合程度較高。

在恒溫恒濕環境下，各預測模型的收縮應變預測值相對于各收縮柱的收縮應變實測值的變異系數見表3。

本文的收縮應變的修正預測模型的平均變異系數僅為7.88%，而ACI 209R(1992)預測模型的平均變異系數達56.97%。利用各預測模型對收縮柱的長期收縮應變進行預測，部分干燥持續時間的預測結果見表4。

在約17 a的混凝土收縮過程中，收縮應變增加較少，本文的修正預測模型增加5.80%，而JTJ 023—85預測模型僅增加1.30%。干燥時間持續至3 a后，混凝土的收縮基本穩定。

1—公式擬合值；2—試驗實測值。

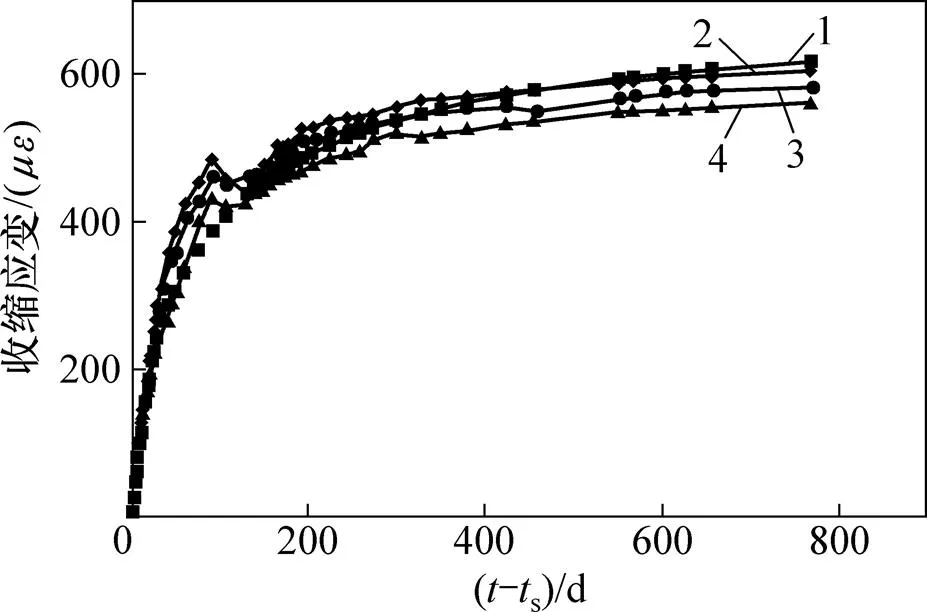
1—修正預測模型；2—SSZ-7號柱實測值；3—SSZ-7-b號柱實測值；4—SSZ-7-a號柱實測值。

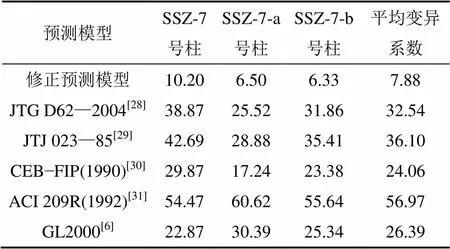
表3 收縮應變預測值相對于實測值的變異系數

注：；；；為第次收縮應變計算值；為第次收縮應變實測值；為第組變異系數；為相對于總體數據的變異系數。

表4 不同預測模型的收縮應變預測結果

3.2 混凝土徐變系數修正預測模型

在恒溫恒濕環境下，以JTG D62—2004徐變系數預測模型為基礎，設混凝土徐變系數的修正預測模型為

基于恒溫恒濕環境下的混凝土徐變試驗，混凝土的徐變修正系數=0.738 7。

1—試驗實測值；2—公式擬合值。

1—SXZ-6號柱實測值；2—SXZ-5號柱實測值；3—修正預測模型。

在恒溫恒濕環境下，各模型的徐變系數預測值相對于SXZ-5號柱和SXZ-6號柱的徐變系數實測值的變異系數，見表5。

表5 徐變系數預測值相對于實測值的變異系數

注：；，；為第次徐變系數計算值；為第次徐變系數實測值；為第組變異系數；為相對于總體數據的變異系數。

本文的徐變系數的修正預測模型的平均變異系數僅為4.42%，而JTJ 023—85預測模型的平均變異系數達56.29%。利用各預測模型對徐變柱的徐變系數進行長期預測，部分持荷時間的預測結果見表6。

表6 不同預測模型的徐變系數預測結果

在約17 a的混凝土徐變過程中，本文的修正預測模型以及JTG D62—2004，JTJ 023—85，CEB?FIP (1990)，ACI 209R(1992)和GL2000等模型的徐變系數分別增加0.135 0，0.182 7，0.050 4，0.202 1，0.184 9和0.440 1。在所有模型中，徐變系數變化最大的為GL2000模型，增大了19.81%，而JTJ 023—85模型徐變系數僅增大1.68%，本文的修正預測模型徐變系數增大7.39%。當持荷時間(?0)達到3 a時，混凝土的徐變基本穩定。

4 結論

1) 對恒溫恒濕環境下的混凝土柱開展收縮徐變試驗研究。混凝土的收縮應變和徐變系數的實測值在前期發展較快，后期逐漸變緩，270d后變化較小。

2) 將長期觀測的混凝土收縮徐變試驗結果與JTG D62—2004，JTJ 023—85，CEB?FIP(1990)，ACI 209R(1992)和GL2000等不同規范模型的收縮徐變預測值進行了對比分析，不同規范模型的收縮徐變預測值相互間差別較大，且均與試驗結果有較大誤差。在幾種常用的混凝土收縮徐變預測模型中，與混凝土收縮試驗結果吻合相對較好的是CEB?FIP(1990)模型，而與ACI 209R(1992)模型吻合度較低；與混凝土徐變試驗結果較吻合的是ACI 209R(1992)模型，而JTJ 023—85模型的徐變預測值與試驗結果相差較大。

3) 以JTG D62—2004預測模型為基礎，引入混凝土收縮修正系數和徐變修正系數，構建了恒溫恒濕環境下混凝土收縮應變和徐變系數修正預測模型，提高了混凝土收縮徐變模型的預測精度。

參考文獻：

[1] 張運濤, 孟少平, 張速. 基于響應面法的橋梁結構徐變效應分析[J]. 中國公路學報, 2011, 24(1): 78?82.ZHANG Yuntao, MENG Shaoping, ZHANG Su. Creep effect analysis of bridge structure based on response surface methodology[J]. China Journal of Highway and Transport, 2011, 24(1): 78?82.

[2] 孫海林, 葉列平, 楊孚衡. 城市軌道交通預應力混凝土連續梁橋的收縮和徐變分析[J]. 公路交通科技, 2005, 22(1): 89?92.SUN Hailin, YE Lieping, YANG Fuheng. Analysis of shrinkage and creep for the continuous PC beam in an urban rail transit bridge[J]. Journal of Highway and Transportation Research and Development, 2005, 22(1): 89?92.

[3] 謝峻, 王國亮, 鄭曉華. 大跨徑預應力混凝土箱梁橋長期下撓問題的研究現狀[J]. 公路交通科技, 2007, 24(1): 47?50.XIE Jun, WANG Guoliang, ZHENG Xiaohua. State of art of long-term deflection for long span prestressed concrete box-girder bridge[J]. Journal of Highway and Transportation Research and Development, 2007, 24(1): 47?50.

[4] 張運濤, 孟少平. 基于響應面法的大跨連續剛構橋長期變形預測[J]. 土木工程學報, 2011, 44(8): 102?106.ZHANG Yuntao, MENG Shaoping. Prediction of long-term deformation of long-span continuous rigid-frame bridges using the response surface method[J]. China Civil Engineering Journal, 2011, 44(8): 102?106.

[5] GARDNER N J, ZHAO J W. Creep and shrinkage revisited[J]. ACI Materials Journal, 1993, 90(3): 236?246.

[6] GARDNER N J, LOCKMAN M J. Design provisions for drying shrinkage and creep of normal-strength concrete[J]. ACI Materials Journal, 2001, 98(2): 159?167.

[7] RASKO P, OJDROVIC, MEHDI S. ZARGHAMEEConcrete creep and shrinkage prediction from short-term test[J]. ACI Materials Journal, 1996, 93(2): 169?177.

[8] 龔洛書, 惠滿印, 楊蓓. 砼收縮與徐變的實用數學表達式[J]. 建筑結構學報, 1988, 9(5): 37?42.GONG Luoshu, HUI Manyin, YANG Bei. Practical mathematical expressions for creep and shrinkage of concrete[J]. Journal of Building Structures, 1988, 9(5): 37?42.

[9] 高政國, 趙國藩. 混凝土徐變分析的雙功能函數表達[J]. 建筑材料學報, 2001, 4(3): 250?255.GAO Zhengguo, ZHAO Guofan. Double function expression of creep model for concrete[J]. Journal of Building Materials, 2001, 4(3): 250?255.

[10] 潘鉆峰, 呂志濤, 劉釗, 等. 蘇通大橋連續剛構收縮徐變效應的不確定性分析[J]. 工程力學, 2009, 26(9): 67?73.PAN Zuanfeng, Lü Zhitao, LIU Zhao, et al. Uncertainty analysis of creep and shrinkage effect in continuous rigid frame of Sutong bridge[J]. Engineering Mechanics, 2009, 26(9): 67?73.

[11] 王德法, 張浩博. 軸拉荷載下混凝土徐變性能的研究[J]. 西安交通大學學報, 2000, 34(3): 95?98.WANG Defa, ZHANG Haobo. Uniaxial tensile creep of concrete[J]. Journal of Xi’an Jiaotong University, 2000, 34(3): 95?98.

[12] 羅許國, 鐘新谷, 戴公連. 高性能混凝土梁長期變形性能試驗研究[J]. 鐵道科學與工程學報, 2005, 2(4): 45?49.LUO Xuguo, ZHONG Xingu, DAI Gonglian. The experimental study on the long-term deformations in high performance concrete beam[J]. Journal of Railway Science and Engineering, 2005, 2(4):45?49.

[13] 鄒超英, 王勇, 胡瓊. 再生混凝土徐變度試驗研究及模型預測[J]. 武漢理工大學學報, 2009, 31(2): 94?98.ZOU Chaoying, WANG Yong, HU Qiong. Experimental study and model predictive of recycled aggregate concrete creep[J]. Journal of Wuhan University of Technology, 2009, 31(2): 94?98.

[14] 余志武, 陳文彬, 羅小勇, 等. 超細粉煤灰高性能混凝土III型軌枕徐變性能研究[J]. 鐵道學報, 2002, 24(5): 107?111.YU Zhiwu, CHEN Wenbin, LUO Xiaoyong, et al. Study on creep behavior of type III sleepers of high performance concrete with ultra-pulverized fly ash[J]. Journal of the China Railway Society, 2002, 24(5): 107?111.

[15] 張運濤, 孟少平, 潘鉆峰. 高強混凝土徐變力學實驗研究[J]. 實驗力學, 2009, 24(6): 592?597.ZHANG Yuntao, MENG Shaoping, PAN Zuanfeng. Experimental study of creep mechanics for high strength concrete[J]. Journal of Experimental Mechanics, 2009, 24(6): 592?597.

[16] 潘鉆峰, 呂志濤, 劉釗, 等. 高強混凝土收縮徐變試驗及預測模型研究[J]. 公路交通科技, 2010, 27(12): 10?15.PAN Zuanfeng, Lü Zhitao, LIU Zhao, et al. Shrinkage and creep tests and prediction model of high-strength concrete[J]. Journal of Highway and Transportation Research and Development, 2010, 27(12): 10?15.

[17] 胡狄, 陳政清. 從短期試驗結果預測新建預應力混凝土梁收縮和徐變的長期效應[J]. 中國鐵道科學, 2003, 24(3): 44?49.HU Di, CHEN Zhengqing. Prediction of Long-term Effect of creep and shrinkage on newly-built prestressed concrete bridge based on short-term test results[J]. China Railway Science, 2003, 24(3): 44?49.

[18] 潘立本, 張蘇俊. 混凝土收縮與徐變的試驗研究[J]. 河海大學學報, 1997, 25(5): 84?89.PAN Liben, ZHANG Sujun. Prediction of shrinkage and creep in concrete[J]. Journal of Hohai University, 1997, 25(5): 84?89.

[19] 葉梅新, 曹建安, 侯文崎, 等. 無碴軌道預應力混凝土梁長期變形及影響因素[J]. 中南大學學報(自然科學版), 2011, 42(6): 1756?1763.YE Meixin, CAO Jianan, HOU Wenqi, et al. Long-term deformation of pre-stressed concrete beams with ballastless track and its in influencing factors[J]. Journal of Central South University (Science and Technology), 2011, 42(6): 1756?1763.

[20] 羅俊禮, 徐志勝, 謝寶超. 不同骨料等級再生混凝土的收縮徐變性能[J]. 中南大學學報(自然科學版), 2013, 44(9): 3815?3822.LUO Junli, XU Zhisheng, XIE Baochao. Shrinkage and creep properties of different grade recycled aggregate concretes[J]. Journal of Central South University (Science and Technology), 2013, 44(9): 3815?3822.

[21] 曹國輝, 胡佳星, 張鍇, 等. 混凝土徐變預測模型修正分析[J]. 建筑結構, 2014, 44(5): 45?49.CAO Guohui, HU Jiaxing, ZHANG Kai, et al. Correction analysis on prediction model of concrete creep[J]. Building Structure, 2014, 44(5): 45?49.

[22] 謝楠, 楊成永, 歐陽杰, 等. 噴射混凝土早齡期徐變的試驗研究及預測析[J]. 工程力學, 2013, 30(3): 365?370.XIE Nan, YANG Chengyong, OUYANG Jie, et al. Experimental research and prediction on shotcrete creep at early age[J]. Engineering Mechanics, 2013, 30(3): 365?370.

[23] 楊健輝, 汪洪菊, 王建生, 等. 高強混凝土收縮徐變試驗及模型比較分析[J]. 工業建筑, 2015, 45(3): 120?125.YANG Jianhui, WANG Hongju, WANG Jiansheng, et al. Shrinkage and creep test and comparative analysis of models on high strength concrete[J]. Industrial Construction, 2015, 45(3): 120?125.

[24] 陳萌, 劉立新, 彭少民. 商品混凝土收縮變形的試驗[J]. 工業建筑, 2007, 37(6): 70?72.CHEN Meng, LIU Lixin, PENG Shaomin. An experimental study on shrinkage deformation for commercial concrete[J]. Industrial Construction, 2007, 37(6): 70?72.

[25] 羅俊禮, 徐志勝, 熊偉. 再生骨料高性能混凝土收縮徐變對比試驗研究[J]. 工業建筑, 2014, 44(1): 79?83.LUO Junli, XU Zhisheng, XIONG Wei. Effective of recycled aggregate on shrinkage and creep of HPC: comparative trail[J]. Industrial Construction, 2014, 44(1): 79?83.

[26] BAZANT Z P, EBICH S. Statistical linear analysis of prediction models for creep and shrinkage[R]. Cement and Concrete Research, 1983(13): 869?876.

[27] BAZANT Z P, BAWEIJA S. Justification and refinement of model B3 for concrete creep and shrinkage: 1.statistics and sensitivity[J]. Materials and Structures, 1995(28): 415?430.

[28] JTG D62—2004, 公路鋼筋混凝土及預應力混凝土橋涵設計規范[S].JTG D62—2004, code for design of highway reinforced concrete and prestressed concrete bridges and culverts[S].

[29] JTJ 023—85, 公路鋼筋混凝土及預應力混凝土橋涵設計規范[S].JTJ 023—85, code for design of highway reinforced concrete and prestressed concrete bridges and culverts[S].

[30] CEB?FIP, CEB?FIP mode code 1990 (design code)[S].

[31] ACI Committee 209 (1992). Prediction of creep, shrinkage and temperature effects in concrete structures[S].

(編輯 陳燦華)

Experimental research on prediction model of concrete shrinkage and creep

HAN Weiwei1, 2, Lü Yigang3

(1.State Engineering Laboratory of Highway Maintenance Technology,Changsha University of Science & Technology, Changsha 410114, China;2. School of Traffic and Transportation Engineering, Changsha University of Science & Technology, Changsha 410114, China;3. Hunan Province Engineering Laboratory of Bridge Structure,Changsha University of Science & Technology, Changsha 410114, China)

Experimental results of concrete shrinkage and creep of long-term observation and prediction values of different code models were compared and analyzed. The results show that according to the results of research, shrinkage and creep increased faster in the early period of experiment and gradually slower later in the environment with constant temperature and humidity. The change becomes smaller after 270 d. There is difference between experimental results of concrete shrinkage and creep of long-term observation and prediction values of different code models. The prediction of concrete shrinkage strain by CEB—FIP(1990) model and prediction of concrete creep coefficient by ACI 209R(1992) model are relatively more accurate. Prediction values of concrete shrinkage strain by ACI 209R(1992) model and concrete creep coefficient by JTJ 023—85 model have a larger deviation from experimental results. Correction coefficients of concrete shrinkage and creep are introduced to modify JTG D62—2004 model based on experimental results. Correction prediction models of concrete shrinkage strain and creep coefficient are constructed with constant temperature and humidity, which can improve the predictive accuracy of prediction model of concrete shrinkage and creep.

concrete; shrinkage; creep coefficient; prediction model; correction coefficient

10.11817/j.issn.1672-7207.2016.10.031

U445.73

A

1672?7207(2016)10?3515?08

2015?11?13；

2016?01?22

長沙理工大學公路養護技術國家工程實驗室開放基金資助項目(kfj140110)；長沙理工大學橋梁結構安全控制湖南省工程實驗室開放基金資助項目(14KD13)；湖南交通科技進步與創新項目(201330)；國家重點基礎研究發展計劃(973計劃)項目(2015CB057705)(Project(kfj140110) supported by Open Fund of State Engineering Laboratory of Highway Maintenance Technology, Changsha University of Science & Technology; Project(14KD13) supported by Open Fund of Engineering Laboratory of Bridge Structure of Hunan Province, Changsha University of Science & Technology; Project(201330) supported byHunan Traffic Science and Technology Progress and Innovation Project; Project(2015CB057705) supported by National Program on Key Basic Research (973 Program) of China)

韓偉威，博士，講師，從事項目管理及混凝土材料耐久性等研究工作；E-mail：55520769@ qq.com