對一道拋物線習題的引申和拓展

貴州省遵義市第五中學　劉承輝

對一道拋物線習題的引申和拓展

貴州省遵義市第五中學劉承輝

在平常的學習中，我們不乏周而復始、簡單重復的解題訓練。對于一些習題，具有較強的示范性。在教學中教師要善于以這些習題為原型，引導學生進行適當引申、拓展和解題后的反思。這樣不僅能充分發掘習題的潛在教學價值，而且對于提高學生學習積極性，培養探索性和創新精神大有幫助。本文僅對一道習題結論加以引申、拓展，供讀者參考。

原題：過拋物線y2=2Px（P＞0）的焦點的一條直線和拋物線相交，兩個交點的縱坐標為y1、y2，求證：y1y2=-P2。

由此結論發現y1y2是一個常數，此結論不難證明（略）。

一、引申

1.原題條件不變，結論變化

（1）x1x2是常數

分析：（如圖1）∵A、B兩交點都在拋物線上

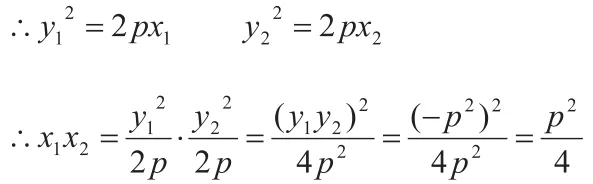
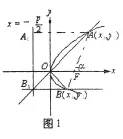
分析：如圖1，由拋物線定義得：

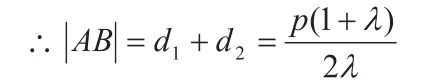
2.條件與結論互換

分析：若AB垂直X軸，結論顯然成立；若AB不垂直于X軸，設直線AB的斜截式方程y=kx+b（k≠0），且A（x1，y1）、B（x2，y2）

二、拓展

例設拋物線的焦點為F，經過點F的直線交拋物線于A、B兩點。點C在拋物線的準線上，證明直線AC經過原點O。

證明：（如圖2）

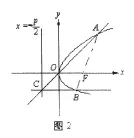
∴直線AC經過原點O

由此可知，對于典型習題結論加以引申、拓展，不僅能收到舉一反三觸類旁通的功效，而且有利于激發學生的學習興趣，培養思維的靈活性和深刻性。