基于改進多目標遺傳算法的船閘調度方法
馮明波
(南通航運職業技術學院,江蘇 南通 226010)
?
基于改進多目標遺傳算法的船閘調度方法
馮明波
(南通航運職業技術學院,江蘇 南通 226010)
針對目前我國內河航運船閘調度采用手工編制調度計劃方式速度慢、調度水平低、缺乏科學性的現狀,通過對單閘多目標調度問題進行建模,并基于改進的SPEA設計了模型求解算法,對船閘調度系統進行優化,為提高船閘通航能力提供了技術支持。
船閘;多目標調度;遺傳算法
0 引言
目前我國內河航運的船閘調度基本采用手工編制調度計劃的方式,調度計劃編制速度慢、調度水平低、缺乏科學性,從而導致船閘使用效率低下,使得本就存在的船閘資源稀缺與航運總量急升之間的矛盾日益加大,極大地制約了我國內河航運的發展步伐。本文對內河航運船閘調度方法進行研究,建立調度問題的數學模型,并基于對調度方案的多角度考慮提出針對調度模型的多目標調度求解算法。
1 多目標船閘調度模型
船閘調度問題可以描述為:在特定時間段內,有若干船舶提出通過船閘申請,調度問題即是在現有船閘空間有限的前提下,合理為每一艘船舶安排通過船閘的時間和空間,從而達到減少船舶等候時間、提高船閘利用效率等目標。
根據調度問題中包含船閘的數量,該調度問題可分為單閘調度和多閘調度,本文主要針對單閘調度展開研究。根據調度范圍的時間特性,船閘調度問題可分為靜態調度和動態調度,本文針對靜態調度問題進行研究。
在對船閘調度問題進行建模時,需要考慮以下問題:
(1)為了簡化問題,本文將所有船舶視為矩形狀且有方向性,即船舶的頭部必須向前。船閘同樣定義為矩形形狀。
(2)為了規避船舶之間潛在的碰撞風險,為每艘船舶定義一個安全區域,即其船身(實際為其對應的矩形框)向外擴展一定的區域,在該區域內不可以安置其他船舶。對于不同的船舶類型,其安全區域大小不同。
(3)待調度船舶具有不同的身份:包含必須在本調度周期安排過閘的船舶(如特殊身份船舶)和一般船舶;包含經過前期多次調度仍未安排過閘的船舶以及本次調度前新加入的船舶。
1.1 變量與符號定義
(1)船閘調度問題所需的符號定義
M:待調度船舶數量;
nc:本調度周期包含的調度閘次數量;
Ll、Wl:船閘矩形的長、寬;
li、wi:船舶i矩形的長、寬;
ldi、wdi:船舶i的安全區域的長、寬;
wti:本調度周期起始時刻船舶i已經等待的時間;
wtiMAX:船舶i允許的最長等待時間;
I:必須在本調度周期安排過閘的船舶序號集合,包括特殊身份船舶和等待時間已經超過規定時限的船舶;
Tc:一個閘次的時間,假設每個閘次的執行時間相等,即Tc為一固定值。
(2)該調度問題的決策變量
xi,j:船舶i在閘次j中安排在船閘中的X坐標;
yi,j:船舶i在閘次j中安排在船閘中的Y坐標;
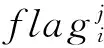
flagi:船舶i在本調度周期是否被調度標識。
上述變量中,xi,j和yi,j分別為船舶左下角點相對于船閘坐標系的X、Y坐標值。船閘坐標定義為:以船閘的左下角點為原點,與船舶按規定停泊后的頭尾連線平行的方向為Y軸,船舶橫向方向為X軸。
1.2 約束條件
船閘調度問題的約束條件如下:
xi,j∈{-1,[0,Wl]}
(1)
yi,j∈{-1,[0,Ll]}
(2)
(3)
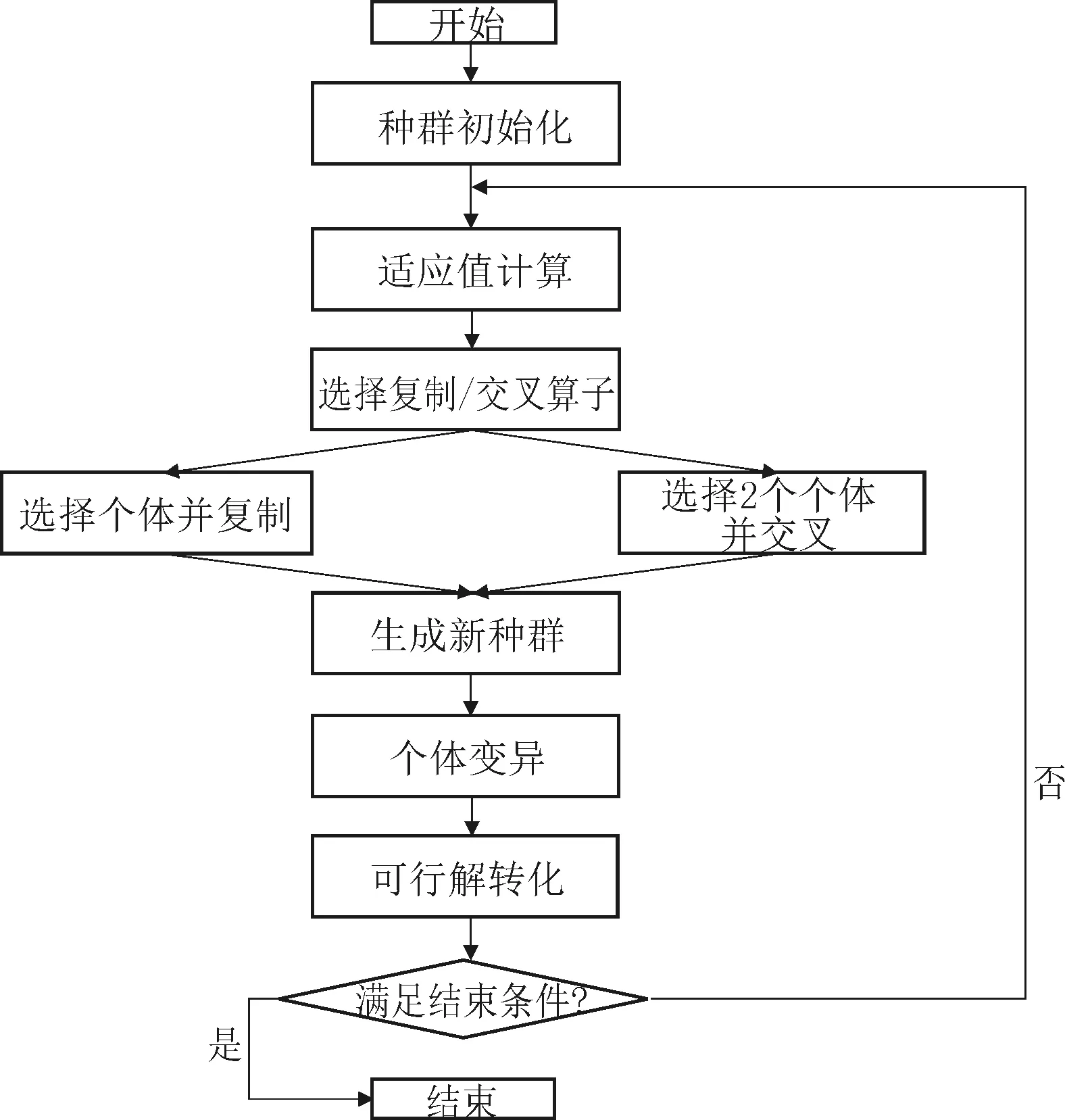
xi,j+wi+wdi (4) yi,j+li+ldi (5) ?i∈Iflagi=1 (6) (7) (8) ?i1,i2∈{1,2,…,M} if (i1≠i2)∧(?j st. (9) (10) (11) 式(9)中定義的Overlapi1,i2表示在同一閘次內調度的兩艘船舶i1和i2是否存在重疊的標識,其計算比較復雜,以下給出詳細計算過程: 為簡化分析過程,假定以船舶i1為參照,判斷船舶i2是否與其有重疊區域。兩船重疊分為2種情況,以船舶i2矩形的4個角點是否至少有1個落入船舶i1矩形區域內進行劃分,如式(12)所示: if (LDIni1,i2)∨(LUIni1,i2)∨(RDIni1,i2)∨ (RUIni1,i2)∨(WInci1,i2)∨(LInci1,i2)∨(AInci1,i2) then LDIni1,i2=true else Overlapi1,i2=false (12) 式中:LDIni1,i2、LUIni1,i2、RDIni1,i2、RUIni1,i2分別為判斷船舶i2矩形左下角、左上角、右下角和右上角是否落入船舶i1矩形內的標識,可統一由下式確定: if (xLDIni1,j else PTlni1,i2=false (13) 式中:xLDi,j、xRUi,j、yLDi,j和yRUi,j分別表示船舶i矩形的左下角和右上角點的X和Y坐標;xPTi2,j、yPTi2,j和PTIni1,i2為形式化變量,分別從{xLDi2,j, xLUi2,j, xRDi2,j, xRUi2,j}、{yLDi2,j,yLUi2,j,yRDi2,j, yRUi2,j}和{ LDIni1,i2,LUIni1,i2,RDIni1,i2,RUIni1,i2}中取值(3個變量取值序號一一對應)從而組成4個公式。其中xLUi,j、xRDi,j、yLUi,j和yRDi,j分別表示船舶i矩形的左上角和右下角點的X和Y坐標。 對于船舶i2矩形的4個角點均未落入船舶i1矩形區域內的情況,又分為2種情況:一是船舶i2在橫向跨度(X方向)上包含i1在橫向上的跨度區域(對應于式(12)的WInci1,i2);二是船舶i2在縱向跨度(Y方向)上包含i1在縱向上的跨度區域(對應于式(12)的LInci1,i2)。如果2種情況均滿足,則對應于船舶i2將船舶i1包含在其矩形框內(對應于式(12)的AInci1,i2)。而情況1與情況2的區別僅在于判斷方向為X軸還是Y軸,因此下面僅以情況1(即WInci1,i2的計算)為例展開分析。滿足情況1的兩船關系又分為4種情形,其中3種情形如圖1所示(第4種情形為船舶i2將船舶i1包含在其矩形框內)。圖中實形框為船舶i1,3個虛形框分別對應于3種情形下船舶i2的位置。這3種情形可統一描述為:在Y軸方向,只要船舶i2的左下角點或者右上角點位于船舶i1的左下角點和右上角點之間即可,因此可由下式確定: 圖1 船舶i2橫向跨越船舶i1時兩者重疊情況示意圖 (14) 而船舶i2在橫向跨度(X方向)上包含船舶i1在橫向上的跨度區域的判斷條件為: (15) (16) 同理: xRUi2,j (17) 在以上計算WInci1,i2和LInci1,i2的公式中均忽略了船舶i2將船舶i1包含在其矩形框內的情形,因此需單獨計算AInci1,i2: AInci1,i2=(xLDi1,j>xLDi2,j)∧(yLDi1,j> yLDi2,j)∧(xRUi1,j (18) 由此,兩船重疊判斷式(12)所需條件均可計算得出。 1.3 調度指標 考慮以下2個船閘調度指標: 一個是從用戶的角度出發,要求所有船舶的等待調度時間盡量短。為了簡便計算,在此僅考慮船舶在本調度周期內等待的時間: (19) 另一個是從交通管理部門的角度出發要求更高的通過率,因此要求在當前調度周期內安排盡量多的船舶過閘: (20) 本文建立的船閘調度模型是典型的NP-hard問題,目前遺傳算法、蟻群算法和粒子群算法等智能搜索算法在該類問題的求解得到了廣泛應用并取得了良好的效果。本文建立的船閘調度模型是一個多目標調度問題,針對這類問題一種簡單的方式是采用加權求和的方式將多目標調度轉化成單目標調度問題,但是正如上一節所介紹,本調度問題所提出的2個指標分別從航運管理部門和用戶角度出發,二者之間在某種程度上存在一定的沖突,難以確定相對權值,該方法存在一定限制。目前針對多目標調度問題應用比較多的是多目標遺傳算法,如NPGA、NSGA和NSGA-II,以及SPEA和SPEA-II等[2-5]。其中SPEA基于Pareto支配理論進行設計,基于“支配個體所有Pareto解所支配個體的數量總和”這一隱含信息對個體周圍的密度進行評價,能夠避免設置其他算法涉及的小生境參數這一難題[6]。本文基于SPEA算法對多目標船閘調度問題進行求解。 2.1 算法流程 本文基于SPEA算法設計多目標船閘調度算法流程如圖2所示。 2.2 染色體編碼與種群初始化 定義染色體:s=[(j1,x1,j1,y1,j1),(j2,x2,j2,y2,j2),…, (jM,xM,jM,yM,jM)],染色體包含M組基因,每組基因為1個三元組,對應于1艘船的調度閘次、在該閘次中安排在船閘的X和Y坐標。染色體長度為3×M,且基因取值-1的大幅度減少。在交叉和變異計算時,以1個三元組基因為單位進行。 圖2 多目標船舶調度算法流程 在進行種群初始化時,要求生成1組對應于模型可行解的染色體,并且盡量使這些可行解具有較高指標,即對應于較優解,為后面的種群進化奠定較好基礎。本文基于貪婪算法思想設計種群初始化策略,該策略生成1個染色體的過程如下: step1:從待調度船舶集合中隨機選取1艘船i; step2:在剩余閘次的空間資源內對船舶i進行排閘; step2.1:在未遍歷閘次集合中隨機選擇1個閘次j; step2.2:調取閘次j的已安排船舶集合Bj,基于式(9)判斷船舶i是否可以安排進閘次j,如是則將船舶i加入集合Bj,并將船舶i安排的閘次j及在船閘中的坐標更新至染色體對應的位置中,進入step3;否則進入step2.3; step2.3:未遍歷閘次集合是否為空,如是則將染色體對應船舶i的基因三元組置為(-1,-1,-1),并進入step3;否則將閘次j從未遍歷閘次集合中去除并返回step2.1; step3:將傳播i從待調度船舶集合中去除。判斷待調度船舶集合是否為空,如是則過程結束,輸出染色體;否則返回step1。 上述過程反復執行N次,即可得到對應于N個可行解的染色體集合,即初始種群。由于該過程在選擇船舶和閘次的過程中均為隨機選取,因此可以產生不同的可行解。 2.3 主要遺傳算子設計 2.3.1 適應值計算 本文對SPEA進行改進,提出個體適應值的計算方法。SPEA存在一個缺點,即容易產生適應值相同的個體,尤其針對幾個相互接近而又不具有Pareto支配關系的個體,SPEA很難有效地區分它們的適應值[7]。這是因為SPEA在針對一個個體進行適應值計算式只考慮到支配該個體的Pareto解,而該個體所支配其他個體的情況并非被考慮,而后者是區分相似個體的重要因素,對此本文對SPEA的個體適應值計算方法進行改進如下: (21) 式中:fitness(xi)為個體的適應值;PDStrSum(xi)為所有Pareto支配xi的個體的強度和(稱為支配解強度和);Str(xi)為xi的強度,即所有被xiPareto支配的個體數量;StrEqu(xi)為所有xi與具有相同支配解強度和的個體集合。 2.3.2 交叉和變異算子 交叉算子以兩個個體相對應的一對三元組為單位執行。為了保持種群的多樣性,針對三元組設計兩種交叉模式:一種是整體交換,即將兩艘船舶被安排的閘次和在閘坐標整體交換;另一種是局部交換,即不改變船舶的原調度閘次,僅交換在閘距離。針對個體I1和I2,交叉算子過程如下: step1:在I1和I2上各隨機選擇基因三元組t1和t2; step2:生成[0,1]之間的隨機數,將該隨機數與事先設定閾值比較,如隨機數大則進入step3,否則進入step4; step3:執行整體交換,即將t1放到I2上而將t2放到I1上,進入step5; step4:執行局部交換,即將I1中t1上的后2個數組成的二元組與I2中t2上的后2個數組成的二元組進行交換,進入step5; step5:針對交叉后的I1和I2上的三元組t1和t2進行微調,即加入較小隨機數。 交叉過程的step5目的是進一步增加種群多樣性,防止種群在船閘少數幾個坐標點附近陷入局部解。為了進一步提高算法的解空間搜索能力,需進一步執行變異操作,變異算子與交叉算子的step5類似,只是加入的是一個較大隨機數,并且在個體的每個三元組均執行變異操作。 算法執行完交叉和變異算子后得到新的種群,但是新種群中個體對應的解是否為可行解難以保證,因此要針對新種群的每一個個體進行可行化轉化,即針對個體上每一個基因三元組對照上一節給出的約束條件組依次判斷是否違反,如是,則將該三元組置為(-1,-1,-1)。 2.4 算法實例驗證 本文基于VC6.0對提出的模型與算法進行了實現,算法運行在IntelCorei7 2.5GHz平臺下,內存為4.0GB,操作系統為Win10。為了模擬多種規模的船舶調度問題,船舶數量和尺寸、船閘尺寸等在給定區間內隨機取值。為了對算法進行驗證,將該算法與基于“先到先服務”原則的貪婪算法進行比較,比較指標C設計如下: C=PD1,2/PD2,1 (22) 2種算法同時運行K次,得到2組各K個調度結果,令本文設計的求解算法序號為1,貪婪算法序號為2,PDi,j表示算法i得到的K個調度結果中Pareto支配算法j得到的K個調度結果的個數之和。因此,C值越大表明算法1的性能越優于算法2。算法運行結果見表1。 表1 算法運行結果 由表1可以看出,在隨機生成的6個實例中,C值均大于1,說明本文提出的算法相比貪婪算法具有明顯的優勢。 本文針對現階段我國內河船閘使用效率低下,導致本就存在的船閘資源稀缺與航運總量急升之間的矛盾日益明顯,極大地制約了我國內河航運的發展步伐等問題,對內河航運船閘調度進行了研究;建立了該問題的調度約束滿足的多目標船閘調度模型,并基于改進的SPEA設計了該多目標調度問題的求解算法;最后通過算法實例驗證了該算法的可行性和有效性,為船閘調度系統優化、船閘的高效運行提供了建議方案和技術支持。 [1] 蔡恩澤. 內河水運“金”濤拍岸[J].決策與信息,2011(5):35-37. [2] 馮明月,李國輝,易先清,等. 一種求解多目標柔性JSP的正交遺傳算法[J].系統仿真學報,2009,21(15):4682-4690. 2016-04-13 江蘇省交通運輸科技項目(2014C03-05) 馮明波(1977—),男,講師,研究方向為輪機管理。 U641.7 A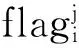

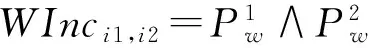
2 多目標船閘調度算法

3 結論

