“三角函數線”在《三角函數》教學中的研究現狀及教學建議

江蘇省揚州市新華中學 (225009)

趙久勇 孟素紅

?

“三角函數線”在《三角函數》教學中的研究現狀及教學建議

江蘇省揚州市新華中學 (225009)

趙久勇 孟素紅

“三角函數線” 是三角函數概念中的一個輔助概念, 是用幾何中的有向線段數值表示三角函數值的一種數形結合方法.現行高中教材《必修4(蘇教版)》第12至13頁中給出了正弦線、余弦線、正切線的定義，其目的是使我們在研究三角函數及解決三角問題時, 既可利用坐標系中代數工具的運算之便, 又可借助單位圓內幾何圖形的性質之利.但教材限于篇幅原因, 對于本可貫穿整個三角學習的三角函數線, 僅在描繪三角函數的圖像、探究三角函數的性質時, 作了部分的應用，給人頗有利器初露鋒芒即告收斂之感，筆者對近年來有關期刊刊登的有關“三角函數線”文章進行梳理，現將研究現狀概括如下：

1 “三角函數線”在三角函數學習中的應用綜述

1.1 解釋三角函數定義

設α是一個任意角，它的終邊與單位圓交于點P(x,y)，則OM=x,MP=y與cosα=x,sinα=y相對照.用單位圓上三角函數線來解釋三角函數，可以使正弦函數、余弦函數從自變量(角的弧度數)到函數值(單位圓上點的橫、縱坐標)之間的對應關系更清楚、簡明，突出了三角函數的本質，也使三角函數反映的數形關系更直接明了，為后續的研究奠定基礎.

1.2 方便記憶三角函數在各個象限內的符號

由三角函數線的作法和三角函數的定義可知，某一個三角函數在同一個象限內的符號是一樣的.如正弦的符號取決于P點縱坐標y的符號，余弦的符號取決于橫坐標x的符號，若P點在第二象限，x<0,y>0.事實上，當P點在第二象限時，正弦線MP方向向上，數量為正，余弦線OM方向向左，數量為負，因此第二象限內的正弦為正，余弦為負；同樣可得正切為負的，其余象限內的三角函數的符號也可一一確定.

1.3 明晰三角函數的定義域

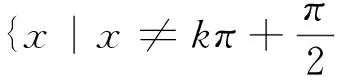
1.4 加深對三角函數性質的理解

即隨著角α值的增大，余弦值相應減小，從而余弦函數在[0,π]上是單調遞減的.正弦函數、正切函數單調性類推可得.

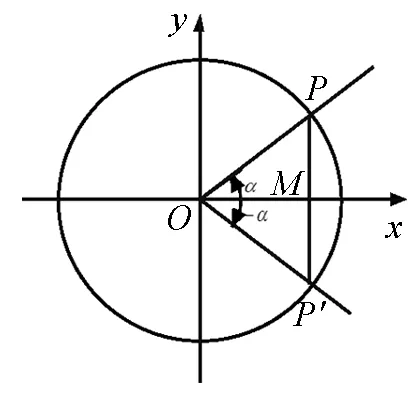
圖1

(3) 奇偶性：如sinα，不論α如何，-α的終邊OP′與α的終邊OP關于x軸對稱(如圖1)，這時，它們的正弦線長短相等，方向相反.即MP′=-MP?sin(-α)=-sinα.同理，余弦函數、正切函數奇偶性類推可知.

1.5 辨別同角三角函數的基本關系

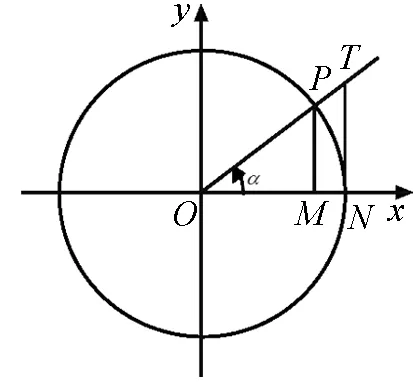
圖2

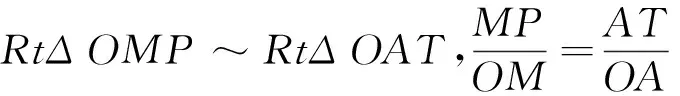
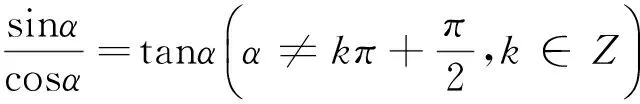
1.6 推導三角函數的誘導公式

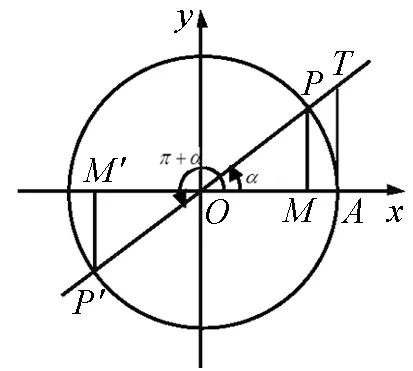
圖3

由于單位圓具有很好的對稱性，因此可以通過對單位圓上對稱點對應的角的三角函數線來推導誘導公式.下面以誘導公式(二)：f(π+α)=±f(α)為例來進行探究(如圖3).

設角α的終邊OP與單位圓的交點為P,則P點關于原點O的對稱點P′也在單位圓上，終邊OP′對應的角是π+α，觀察角α和π+α的各三角函數線，正弦線分別是MP和MP′，余弦線分別是OM和OM′，正切線都是AT，且MP=-MP′,OM=-OM′，即有sin(π+α)=-sinα,cos(π+α)=-cosα，tan(π+α)=tanα.

2 “三角函數線”在解決數學問題中的應用

2.1 求三角函數的值

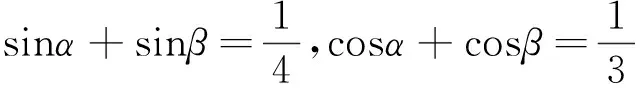
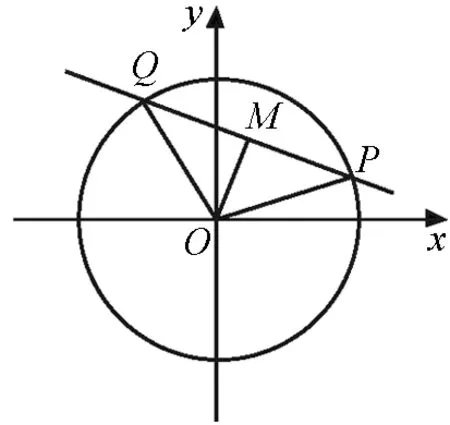
圖4

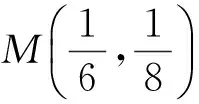
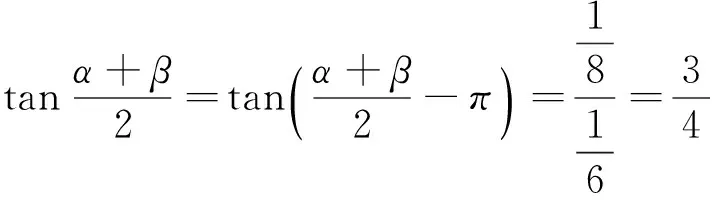
2.2 比較三角函數值的大小

例2 設α∈[0,2π) ，試比較sinα與cosα的大小關系

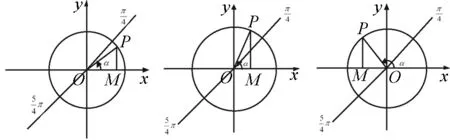
圖5-1 圖5-2 圖5-3

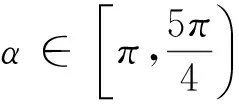
|OM|(如圖5-4)，MP>OM,即sinα>cosα;

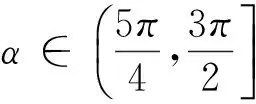
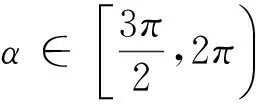
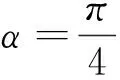
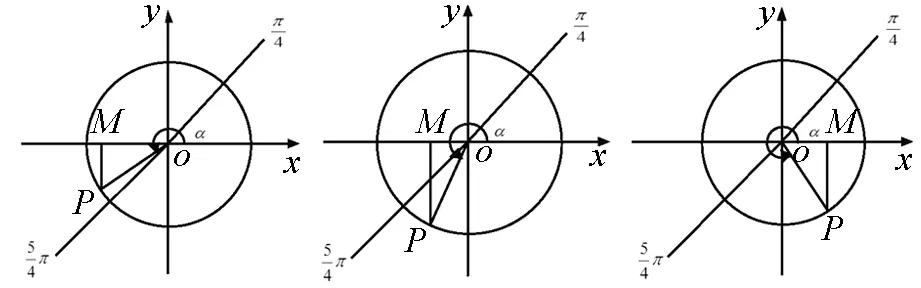
圖5-4 圖5-5 圖5-6

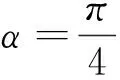
2.3 解三角不等式

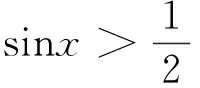
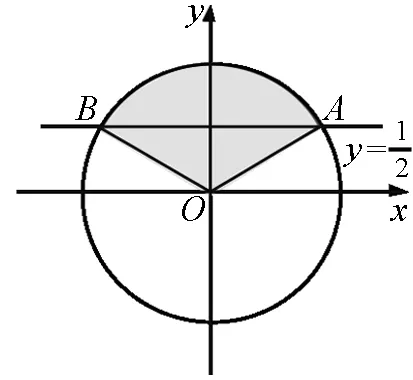
圖6

2.4 證明三角等式和不等式

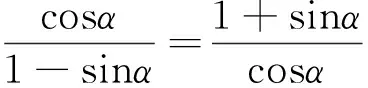
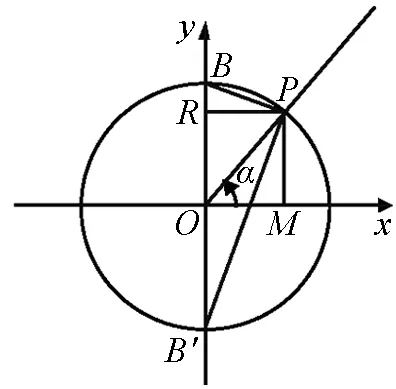
圖7

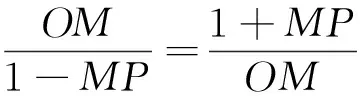
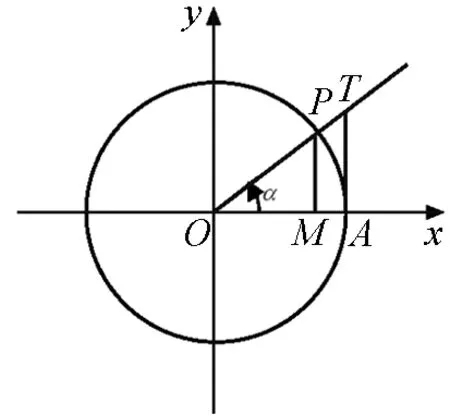
圖8

3 教學建議

縱觀以上研究，“三角函數線”的教學對學生的解題有很大幫助.但為使學生對于“三角函數線”定義的理解及生成過程不再疑惑重重, 為使學生在透徹理解定義的基礎之上，更加清晰的應用其解題.

筆者認為教師在教學時需注意以下幾個問題：

問題1 為什么用單位圓，其他圓是否可以？

問題2 為什么過點A(1,0)作單位圓的切線？過其他點是否可以？

圖9

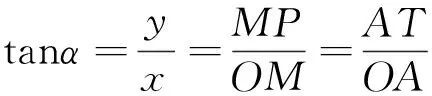
問題3 為什么當α為第二、三象限角時切線交其反向延長線于點T?

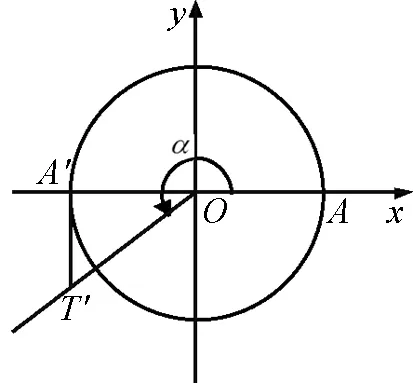
圖10

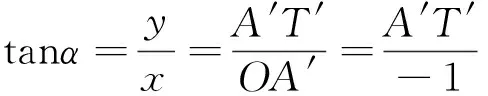
圖11

4 教學嘗試

當然，在本屆高一教學中，為了更好的便于學生對“三角函數線”的理解及應用，我嘗試將教材中所介紹的“三角函數線”作了適當的修改(保留其使用幾何圖形來理解三角的思想).操作如下：

定理 sinα=α的終邊與單位圓交點的縱坐標；cosα=α的終邊與單位圓交點的橫坐標； tanα=α的終邊(或反向延長線)與單位圓正切線(過A與單位圓相切的直線)交點的縱坐標.

圖12 圖13

證明：(如圖12)作單位圓，設角α終邊與單位圓交點為P1(x1,y1).因為r=1，由正、余弦函數定義知sinα=y1,cosα=x1；(如圖13)設角α終邊與單位圓正切線交點為P2(1,y2)，由正切函數定義知tanα=y2.

上述定理具有以下兩大優點:

一.定理推導簡便，推導過程中只用學生剛學過的三角函數定義，學生容易理解和掌握，同時對鞏固三角函數定義也起到了積極作用.不需再引入“有向線段” 的有關概念，產生過程自然易懂，學生很容易接受.

二.定理完全能夠很好的保留“三角函數線”的幾何作用，而且應用范圍更廣.由于定理是將三角函數值與相關點的一個坐標直接對應，使用起來非常方便.除了作三角函數圖像以外，還可輕松解決判斷三角函數值的正負、比較三角函數的大小、已知三角函數值求角、解三角不等式等.

[1]陳曦，張海玲，王尚志.HPM 視角下“任意角三角函數的概念”教學研究[J].首都師范大學學報( 自然科學版)，2014，12(第35卷第6期)：23-27.

[2]王學先.三角函數中有趣的“楚河漢界”———“三角函數線”數學拓展型新課教學過程簡錄及評析[J].中國數學教育,2012,6:28-32.

[3]田新.三角函數線[J].數學通訊,1996,11:1-3.