一堂習題課的“節外生枝”

安徽省五河縣第一中學 (233300)

張同語

?

一堂習題課的“節外生枝”

安徽省五河縣第一中學 (233300)

張同語

數學教學，離不開解題教學，解題教學的過程正是思想交流，思維碰撞的過程，思維的發散與發展，能力的提煉與提升往往是難以預設的，如果把控不好，也會弄得“一發不可收拾”，還會被學生“牽著牛鼻子走”.

一、案例描述

在上完三角函數后，筆者開設了一堂習題課，在引導學生系統梳理這一章的知識網絡后，出示了這樣一道例題：

教師：請同學們認真審題，從式子的結構特征看，與我們學過的哪些知識有關？

學生1：式子的結構特征與我們學過的誘導公式相近，因此，可以用誘導公式解答，但是，需要對n的奇偶性進行分類.

教師：很好，學生1觀察的很仔細，分析的很到位，通過確定n的奇偶性，消除了與誘導公式的差異，請將你的思路在黑板上展示出來.

學生1解：①當n=2k(k∈Z)時,

②當n=2k+1(k∈Z)時,原式=

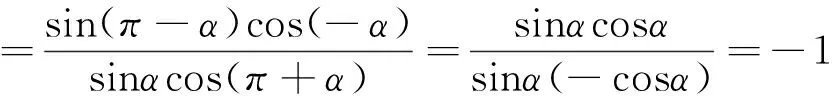
教師：學生1解這道題用到了什么數學思想？

眾學生：分類討論思想，化歸轉化思想.

教師：正確，請看下一例題.

學生2：老師，這道題可以用換元思想整體處理，回避分類討論.

教師(猶豫了一下，感覺是個好方法)：好主意，請你展示一下.

學生2：由所給數學式的結構特征,不妨設nπ-α=θ,則可回避分類討論.

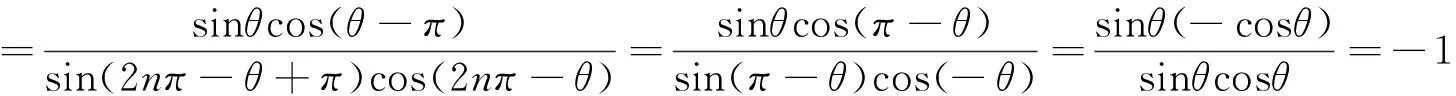
教師：學生2通過換元，將一串式子用一個字母表示，換元以后，式子大大地得到簡化，回避了分類討論，是個絕妙的方法，值得表揚.

正當筆者準備講解下一例題時，學生3又舉手說：老師我也有一種解法：所給數學式中出現nπ-α,nπ+α,(n-1)π-α,(n+1)π+α四個角.顯然角nπ-α與角nπ+α終邊關于x軸對稱,角(n-1)π-α與角(n+1)π+α的終邊關于x軸對稱,角(n-1)π-α與角nπ-α終邊關于原點對稱.若設角nπ-α的終邊與單位圓的交點為P1(x,y),則nπ+α,(n-1)π-α,(n+1)π+α三個角的終邊與單位圓交點依次為P2(x,-y),P3(-x,-y),

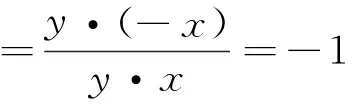
教師：學生3回歸定義,厚重深刻，鞭辟入里,入木三分，說明學生3對數學概念的理解非常深刻，令人欽佩.

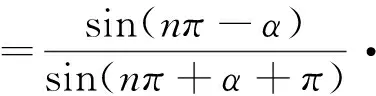
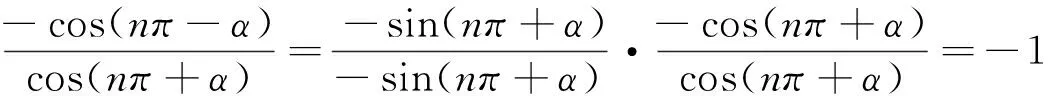
教師：學生4聯想豐富,數形結合，融會貫通,形象直觀，這種聯想是學習數學不可或缺的，請大家用掌聲鼓勵一下.

至此，筆者準備的教學計劃被打亂了，后面準備的一些內容沒有完成.

二、教學感悟

回想這節課，我就是因為一個問題的拋出差點兒失控.雖有所“失”，但更有所“得”——令我高興的是，我只是一個小小的“順應民意”，卻收到意想不到的驚喜.——我感覺同學們從來沒有過這種“課堂主人”的幸福，滿心欣慰油然而生——“原來，課還可以這樣上！”.

實際上，課堂教學不需要什么“模式”！相反，打破程式化教學模式，根據學生的需要因勢利導的來一個小小的“改變”，可能會牢牢的抓住學生的“牛鼻子”.比起在那里唱著“獨角戲”，做著無用功，不知要強多少倍.這，或許就是我們說的“生本課堂”吧.

反思我們平日的教學，為了追求“高效”，經常會一個勁兒的朝著“考點”方向不轉彎.最后弄得個“滿堂灌”，“口頭灌”到“電子灌”.

就數學課而言，有的教師可以“高效”到沒有任何枝枝蔓蔓，有時候簡單到一句廢話也沒有——走進教室，沒有了“上課”口令，沒有了“起立”和“坐下”，單刀直入地進入主題：“請打開課本第……面，今天我們學習……”就開始了他的上課.試想一下，這樣蒼白無趣的上課怎么會引起學生的興趣呢？學生沒有興趣，教師那不就只得靠自身拼命地“灌”嗎？有時候，口中說讓學生參與，卻真正參與時舍不得放手，生怕耽誤了寶貴的“掙分數”時間.

其實，當教師的還要學會當一當學生，在現實教學情境中經常性的換位思考：假如自己坐在下面聽報告，像這樣無滋無味的開頭，你又是什么感受？這樣的場合里，就連尚有一定自制力的成人們都難以堅持下來，何況還是未成年的中學生呢？假如正在興致上一個問題被老師強行拽著轉彎，你又會有什么感受？

回顧這一堂課，雖然沒能完成事先“預設”的全部內容，但是，課堂上一石激起千層浪，喚起了學生“沉睡”已久的求知欲.至少在他們的記憶里留下了值得回憶的45分鐘.試想，課堂上如果能經常有這樣的精彩，即使再多一點“浪花”和“插曲”又何妨呢？