誘導學生發現新知的一個數學教學案例

浙江省寧波市北侖區明港中學 (315800)

王翠娜

?

誘導學生發現新知的一個數學教學案例

浙江省寧波市北侖區明港中學 (315800)

王翠娜

關注數學發現的教學是數學教育的研究熱點，這不僅與數學課程目標中提出的過程目標有關，更是因為數學教學的本質就是讓學生在教學體驗中發現新知并培養終生持續發展的潛質.本文通過一道例題引發一個教學案例，揭示教師如何誘導學生發現新知的嘗試策略，供參考！

案例實錄

老師借助信息技術出示此題，指點同學們畫出示意圖并思考解題思路.大約經過四分鐘，教師提出解題的大致思路.

生1：在線段0A2上取動點K為焦點，從而可得M點坐標，再代入驗證.

生2：作為選擇填空題可以選擇特殊點的方法，而作為解答題，必須體現M的任意性.

教師：這位同學說得非常好！從“特殊”到“一般”是我們認識事物的一般規律，但對于事物的本質屬性我們必須加以論證才能得到結論.而僅僅從“特殊”到“一般”而下結論往往使我們犯下“以偏概全”的錯誤.作為解答題，必須體現M的任意性.

教師：這道解析幾何題的不變圖形是什么？

生3：不變圖形是橢圓(其中包括長軸A1A2是固定的).

教師：如何區別主動點、從動點、目標動點？

生4：點K是主動點，點P、Q都是從動點，點M是目標動點.

教師：用什么辦法求動點M的軌跡方程？

生5：設主動點K的坐標，聯立兩條直線的方程，考慮交點M的坐標，用參數法.

教師請生5上黑板解答，要求其余學生在下面做.生5的解答如下——

圖1

如圖1，教師演示幾何畫板，檢驗證題結果的正確性，誘導學生觀察題設橢圓與雙曲線的聯系.

教師：生5的證明過程還可以改進，請看——

學生拍手稱快！

教師：這道題的證明過程還可以進一步整體改進，下節課我們來揭秘之；如果將題目改編為求交點M的軌跡，同學們，你們該如何回答？

教師：回答正確！請大家總結一下本題的解題思路，當時你為什么沒想到？今后在解決“任意性”問題時該如何處理？

教師：同學們能否將本題的條件、結論一般化？

生7：……(學生口述).

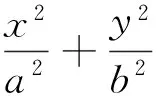
教師：該題的證明思路與上題比較關系如何？

生8：與上例完全一致，點K是主動點，點P、Q都是從動點，點M是目標動點.

教師讓同學們自行完成解答過程，檢查后，整理如下.

教師：我們把此題再來進一步研究，如果對上述條件與結論互逆，那命題應該怎樣敘述？

教師：同學們，此命題是否正確？

學生們在下面嘀咕道，有膽大的學生說：這樣的垂線與雙曲線沒有交點！

教師：很好，既然K在實軸A1A2上垂線PQ與雙曲線沒有交點，那么應該怎樣合理規定K的位置呢？

生10：(很興奮)K應該在x軸去掉實軸A1A2所剩余的兩條射線上.

教師：太棒了！同學們平時要對自己有信心,要勤動腦，激發自己思維的火花.

生11：……(口述結論).

教師：請同學們課后驗證這個結論.

教師小結：一道例題，只要我們更深入地挖掘，往往會有意外的收獲.這樣的方法，我們要在平時解題過程中積極培養，而不能解完一個題目就以為大功告成，這樣容易事倍功半.對問題進行拓展、逆向、類比的再思考，就可以解答一道問題而領會一類問題，從而收到事半功倍的效果.上述教學片斷我們探究到兩個類比結論(教師再集中演示)——

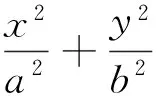
教師：上面已經預留了兩個課后問題(別法證引例，補證命題2)，現在再請同學們課后思考能否把命題1、命題2統一起來表述，明天回答我.

案例分析

上述教學片斷用了大約半節課的時間，從學生的表現來看，能夠感受到他們對本節課教學內容收獲頗多，也使得自己感到欣慰.作為一名數學教師，在平時的數學課堂教學中，我一直在嘗試如何讓自己的數學課堂活躍起來，如何誘導學生在新知識的探索過程中做到自我感悟、自我建構，讓學生在課堂上真正地“動”起來，引發他們強烈的探究意向，喚起學生高漲的學習激情，調動學生學習求知的內驅力，推動學生主動地探究獲取新知.下面我談談自己的幾點體會.

(一)通過“變式”以關注數學教學的“數學化”過程來誘導學生發現新知

數學教學應是數學活動過程的教學，突出過程，就是強調知識體系的形成過程，強調數學思維與方法的形成過程，盡管關于關注數學過程的教學的理解各有差異，但本質是一致的，即在教學過程中，建立在教材的基礎上，為學生設置一個能夠展現數學思維過程的教學設計，使得學生能在其中的情感體驗，進而參與數學理論的探索.而“變式”可以使“再發現”的過程既簡約又有效，使數學知識的本質特征更加顯露突出，有利于學生“透過現象看本質”，使學生更容易地發現“變化中的規律性”，不是借用空洞的教條而是經過實實在在的“數學化”過程來讓學生體驗數學探究的樂趣、收獲數學探究的新知.數學教育家(G.Polya)波利亞認為：“中學數學的主要任務就是加強解題的訓練.”“掌握數學就意味著善于解題.”因此需把原來的題目變成“長留活水”.對于一些典型問題解題后，改變原題的結構或作適當的引申變換，往往可使一題變成一串，激發學生把問題想得更廣、想得更深.

(二)通過激發興趣，誘導學生思維走向縱深，發現新知

興趣是最好的老師，是學生學習的強大動力，當教師能駕輕就熟地在教學中創設情景，那他就是學生心目中的“英雄”，他所教的數學課也將是學生最感興趣的課程.應當承認，一方面數學的高度抽象性、嚴密的邏輯性、結論的確定性與應用的廣泛性等特征，決定了數學的難度，它往往使初學者望而卻步.但為了培養學生對數學的興趣，在教學中一定要遵循循序漸進的原則，遠離超標內容；遠離偏題、怪題.注重本班學生的實際，從學生的實際興趣出發，與課堂內容有機地結合起來.只有學生對數學感興趣時，才能孜孜不倦、全神貫注地沉浸于求知的境界之中，才能激發學生智慧的火花，這樣教師就可以盡可能放手讓學生自主探究，必要時教師給予適當的引導，使學生的思維進一步得到深化.

(三)通過觀察、思考、討論等形式誘導學生參與知識形成發展的全過程，盡可能增加學生的參與機會，發現新知

在數學教學中，促使學生眼、耳、鼻、舌、身多種感官并用，讓學生積累豐富的典型的感性材料，建立清晰的表象，才能更好地進行比較、分析、概括等一系列思維活動，進而真正參與到知識形成和發展的全過程中來.具體做法可以參考如下：

1．讓學生多觀察.數學雖不同于一些實驗性較強的學科，比如物理、化學學科能讓學生直接觀察實驗情況，得出結論，但數學教師在平時教學過程中對概念的概括抽象，數學公式的發現推導，數學題目的解答論證，都可以讓學生多觀察.

2．讓學生多思考.課堂教學中概念的提出與抽象，公式的提出與概括，題目解答的思路與方法的尋找，問題的辨析，知識的聯系與結構，都需要學生多思考.

3.讓學生多討論.課堂教學中，教師的質疑、討論、設問可討論，問題怎樣解決可討論.通過討論，學生間可充分發表自己的見解，達到交流進而共同提高的效果.

此外，教學中讓學生多練習、多提問、多板演等都可增加學生參與的機會.

總之，在數學課堂教學活動中要優化師生的共同行為，為學生創設主動參與的機會，提供主動發展的空間，引導學生的主動參與，從而落實學生的主體地位，促進學生的主動發展，誘導學生在自主的空間內獲取新知，起到事半功倍的教學效果.