多用方程來解題

□邱廷建

多用方程來解題

□邱廷建

小朋友，在解答一些問題時，用算術方法解答往往比較繁鎖困難，如果運用方程來解答，會簡單很多，我們一起來學習吧！

一、轉化為方程解決問題

一些等式含有兩個或兩個以上相同的未知數，我們比較難找到解題的途徑，但如果把相同的未知數設為x，轉化為方程來求解，就很容易解決問題。

例1.在下面的兩個□里填入相同的數，使等式成立。

［分析與解］可以把□里的未知數用同一個字母來表示，這樣就可以轉化為方程來解答。設□里的數為x。可列方程25x－16x＝54，解得：x＝6。

二、順向思考列方程解決問題

一些需要逆向思考來解決的問題，如果用算術方法解答往往比較繁鎖，也容易出現差錯。因此我們可以順向思考列方程來解決問題，這樣可以化難為易，也能顯示出方程解法的優越性。

例2.一個長方形的周長是30厘米，長是寬的2倍。這個長方形的長和寬各是多少厘米？

［分析與解］如果用算術方法解答，就需要逆向思考，容易出現差錯，因此我們可以順向思考，根據“（長+寬）×2＝長方形的周長”這個公式列方程。設長方形的寬為x厘米，長為2x厘米。可列方程（2x+x）×2＝30，解得：x＝5，所以2x＝2×5＝10。這個長方形的長是10厘米，寬是5厘米。

例3.心里想一個數，把它乘3，再減去18，等于57。心里想的這個數是多少？

［分析與解］可以順向思考，根據“一個數先乘3，再減去18，等于57”列方程解決這個問題。設心里想的這個數為x。可列方程3x－18＝57，解得：x＝25，即心里想的這個數是25。

例4.下面是一張撕掉一角的發票，你能算出每把椅子的單價嗎？

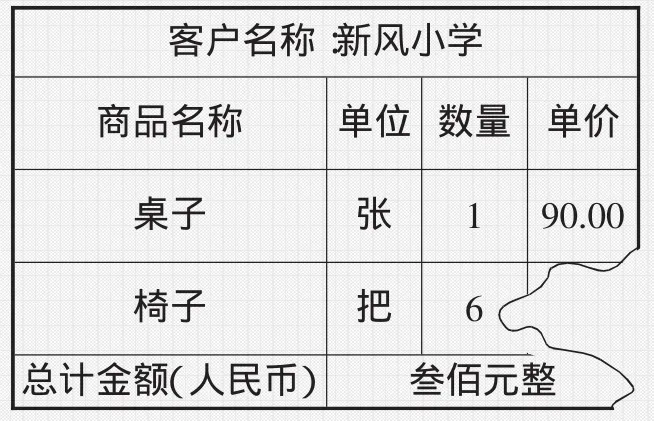
［分析與解］可以順向思考，根據“桌子的錢數+椅子的錢數＝總錢數”列方程解決這個問題。設每把椅子的單價是x元。可列方程90+6x＝300，解得：x＝35，所以每把椅子的單價是35元。

三、用不同思路列方程解決問題

列方程解決問題，要先找出題中數量之間的等量關系，然后列方程求解。由于分析思路不同，找出的等量關系也不同，因此可以列出不同的方程。所以我們在學習列方程解決問題時，要學會尋找不同的等量關系，用不同的方程解決同一問題。

例5.地球繞太陽一周要用365天，比水星繞太陽一周用的時間的4倍多13天。水星繞太陽一周要用多少天？

［分析與解］改變敘述方式，把題目中敘述條件的形式作適當變換，找出不同的等量關系。

這道題可以敘述成：水星繞太陽一周所需時間的4倍加上13天等于365天。設水星繞太陽一周要用x天。可列方程4x+13＝365，解得：x＝88，所以水星繞太陽一周要用88天。

這道題也可以敘述成：365天減去水星繞太陽一周所需時間的4倍等于13天。設水星繞太陽一周要用x天。可列方程365－4x＝13，解得：x＝88，所以水星繞太陽一周要用88天。

這道題還可以敘述成：365天減去13天與水星繞太陽一周所需時間的4倍相等。設水星繞太陽一周要用x天。可列方程4x＝365－13，解得：x＝88，所以水星繞太陽一周要用88天。

（本文作者為福建省上杭縣教師進修學校特級教師）

第14頁參考答案

76.5+1.56＝78.06（元），78.06元＞78元，他們的錢夠用。