平直節理黏結顆粒材料宏細觀參數關系及細觀參數的標定

陳鵬宇 余宏明

摘 要：為了分析平直節理黏結顆粒材料宏細觀參數關系以及進行細觀參數的標定，以單軸壓縮、直接拉伸和雙軸壓縮數值試驗作為宏觀參數測試方法，對平直節理接觸模型細觀參數進行正交設計，采用多因素方差分析和回歸分析研究宏細觀參數之間的關系，在此基礎上，建立了細觀參數的標定方法。以灰巖的室內試驗為基礎，對其細觀參數進行標定，模擬結果與試驗結果相接近，驗證了方法的有效性。

關鍵詞：顆粒流；平直節理接觸模型；巖石；宏觀參數；細觀參數

中圖分類號：TU457

文獻標志碼：A文章編號：1674-4764（2016）05-0074-11

Abstract： The orthogonal design and multi-factor analysis of variance is adopted to analyze the relationship between macroparameters and microparameters of flat-jointed bonded-particle material and to establish the calibration method of microparameters. Firstly， the orthogonal design is adopted to conduct the macroparameters of flat-jointed contact model and the uniaxial compression， direct tension and biaxial compression numerical test is used to calculate the macroparameters of rock. Then multi-factor analysis of variance and regression analysis are adopted to analyze the relationship between macroparameters and microparameters. On this basis， calibration method of microparameters for rock is proposed in this paper. Based on laboratory tests of limestone， the microparameters of limestone are calibrated. The simulation results are closed to the laboratory test results， and this validated the significance of the proposed method.

Keywords：PFC； flat-jointed contact model； rock； macroparameters； microparameters

二維顆粒流模型由一系列的圓形顆粒組成，通過它們之間的相互作用來模擬材料的宏觀力學性質。為了正確反映巖石的宏觀性質，需要選擇合理的接觸本構模型及其細觀參數。最初，顆粒接觸黏結模型中只有接觸黏結模型和平行黏結模型兩種[1]，但是在實際應用中發現這兩種模型所得出的單軸抗壓強度和單軸抗拉強度比值（UCS/TS）為3～4，低于許多巖石的UCS/TS（一般超過10）[2]。為此，Cho等[3]提出了簇平行黏結模型，該模型將多個黏結顆粒聚集成簇，簇中單個顆粒的旋轉被抑制，使得UCS/TS值顯著增大。Potyondy[4]則提出了一種適用于硬質巖石的平直節理顆粒黏結模型，將圓形顆粒構造成多邊形顆粒，顆粒破壞后的旋轉被抑制，使得UCS/TS值顯著增大。為此，本文選用平直節理接觸模型作為模擬巖石的顆粒接觸本構模型。

在顆粒流數值模擬中，細觀參數的標定是最重要的準備工作之一，其關系到是否能夠正確模擬材料的宏觀力學性質。目前，多通過研究黏結顆粒材料宏細觀參數之間的關系來實現細觀參數的標定。Yoon等[5]研究了接觸黏結顆粒材料宏細觀參數的關系。顏敬等[6]研究了無黏結顆粒材料宏細觀參數的關系。周喻等[7]、越國彥等[8]、曾青冬等[9]、叢宇等[10]研究了平行黏結顆粒材料中細觀參數對宏觀特性的影響。夏明等[2]研究了簇平行黏結顆粒材料中細觀參數對宏觀參數的影響。這些研究都為細觀參數的標定提供了依據，但其研究成果均未涉及平直節理接觸模型。為此，筆者以平直節理黏結顆粒材料為研究對象，通過正交試驗設計、多因素方差分析和回歸分析研究其宏細觀參數之間的關系，并建立細觀參數的標定方法。

1 二維顆粒流基本理論

1.1 平直節理接觸模型

二維顆粒流模型中平直節理接觸模型能夠抑制黏結破壞后顆粒的旋轉，這是與接觸黏結模型和平行黏結模型的最大區別。典型的平直節理接觸模型如圖1所示。

1.2 巖石數值試驗

巖石數值試驗的目的是與室內試驗結果進行對比以實現細觀參數的標定。單軸壓縮數值試驗（圖2）是經由宏觀參數得到細觀參數的最重要途徑之一，可以得到單軸抗壓強度、變形模量和泊松比等參數，根據數值試驗的應力應變曲線可得到平面應力狀態下的變形模量和泊松比，其中，變形模量采用割線模量表示，在數值試驗中易于計算，利于數值試驗和室內試驗的對比分析，計算公式見式（3）～（5）。

除了直接拉伸數值試驗以外，也可以通過間接拉伸（巴西劈裂）數值試驗，如圖4所示。根據數值試樣破裂時的峰值作用力Ff，可得數值試樣的抗拉強度，計算公式見式（6）。

σt=2PπDL（6）

式中：σt為試樣抗拉強度；P為試樣破壞荷載；D為試樣直徑；L為試樣高度。

由于巴西劈裂和直接拉伸所測的抗拉強度之間存在較大差異，為了獲得準確的抗拉強度，數值試驗時采用直接拉伸測定抗拉強度。

雙軸壓縮數值試驗（對應于巖石三軸壓縮試驗）可確定強度參數C、tan φ，雙軸壓縮數值模型如圖5（a）所示。定義4道墻作為邊界條件，固定上下邊界墻（圖5中，1、2墻）豎直方向速率（加載速率），即可對數值試樣施加法向荷載，恒定的圍壓可通過伺服系統程序不斷地調整左右邊界墻（圖5中，3、4墻）的位移速度實現。通過設定不同的圍壓進行數值試驗，如圖5（b）所示，采用摩爾庫倫屈服準則（M-C屈服準則）即可確定強度參數。

2 宏細觀參數之間的關系

顆粒流模型由顆粒組成，模型的宏觀參數是由顆粒和黏結的細觀參數決定，兩者之間具有相關性。目前多采用試錯法確定細觀參數，即對比室內試驗和數值試驗的結果，通過不斷調節細觀參數，以達到可接受的精度范圍。也有研究通過回歸分析[5]和BP神經網絡模型[7]反演細觀參數，但都是針對比較簡單的接觸黏結模型和平行黏結模型，需要確定的細觀參數較少。本文的研究對象為平直節理接觸模型，其主要細觀參數包括：N、Ec、kn/ks、μb、λ、σb、cb、φb。其中：N 為交界面段數；Ec為平直節理模量；kn/ks為平直節理剛度比；μb為平直節理摩擦系數；λ為平直節理兩端較小顆粒的半徑比；σb為平直節理抗拉強度；cb為平直節理粘聚力；φb為平直節理內摩擦角。

平直節理接觸模型細觀參數較多，如果盲目地調節細觀參數，有可能導致大量數值試驗，增加建模的難度。為此，可通過研究平直節理黏結顆粒材料宏細觀參數之間的關系，為細觀參數的標定提供依據，從而降低試錯法數值試驗的數量，更快捷的確定細觀參數。

2.1 正交試驗設計

正交試驗設計根據正交性從全面試驗中挑選出部分有代表性的點進行試驗，可以在很大程度上減少數值試驗的數量[12]。在進行正交試驗設計之前，考慮到平直節理黏結顆粒材料細觀參數較多，增加了數值試驗的數量和細觀參數標定的難度，有必要進行一定的假設，以減少細觀參數的數量。參考Potyondy[4]、Poulsenn等[13]的研究，作以下假設：

1）平直節理抗拉強度小于抗剪強度，即σb<τb=cb+σtan φb （可獲得符合實際的巖石拉壓強度比）；

2） 平直節理兩端較小顆粒的半徑比λ = 1；

3）取最小粒徑Rmin = 0.5 mm，顆粒半徑比固定為1.66；

4）平直節理交界面段數N=4；

5）顆粒密度取2 700 kg/m3；

6）顆粒接觸模量、剛度比和摩擦系數同平直節理一致。

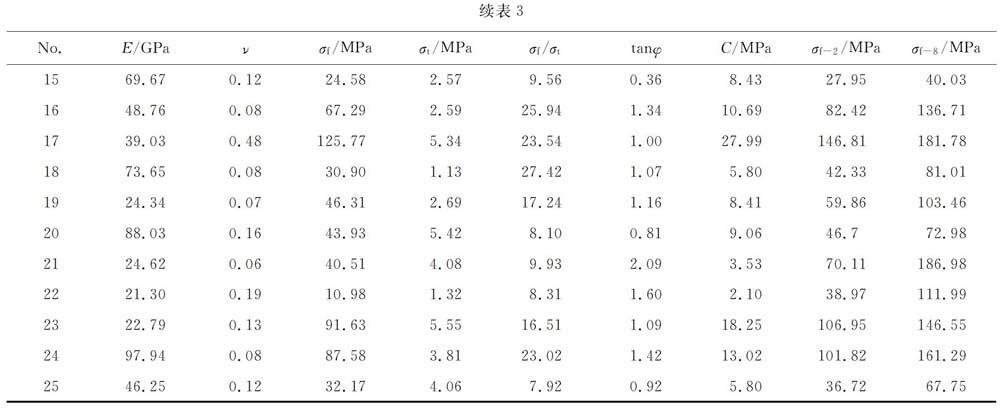
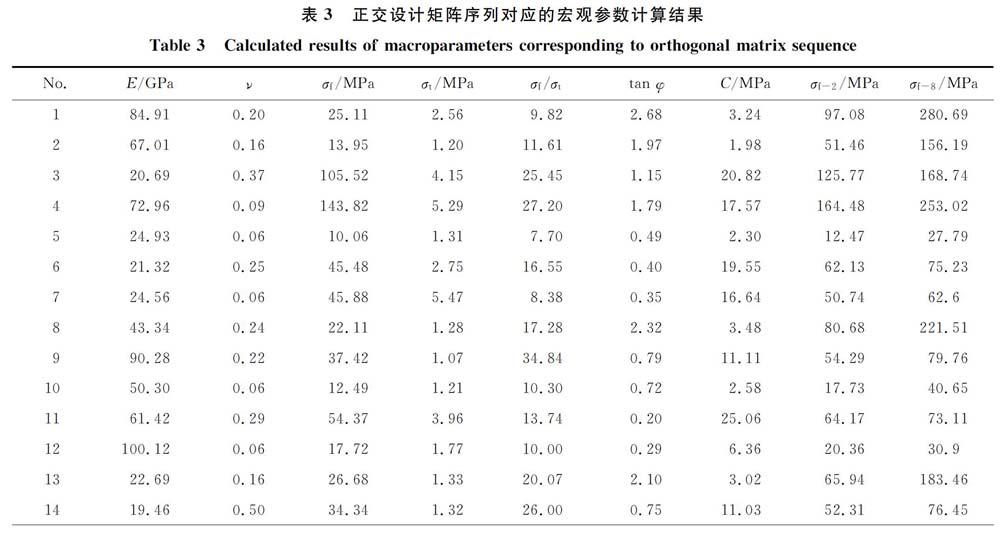
由此，根據所需確定的細觀參數建立正交試驗設計表（表1），設計的正交矩陣序列如表2所示。分別進行單軸壓縮、直接拉伸和雙軸壓縮數值試驗（試樣寬50 mm，高100 mm），加載速率0.01 m/s。由此得到宏觀參數：變形模量E、泊松比v、單軸抗壓強度σf、抗拉強度σt、內摩擦系數tan φ和內聚力C。這樣細觀參數和宏觀參數都是6個，降低了細觀參數標定的不確定性。數值試驗所得結果如表3所示，符合大部分巖石的宏觀參數取值范圍。

2.3 回歸分析

根據上述正交試驗計算結果可以建立宏觀參數與其主要顯著影響因素之間的關系式。取顯著性水平為α = 0.05作為回歸系數檢驗的標準，若某系數的相伴概率值Sig. > 0.05，則在回歸分析中去掉對應的細觀參數，直到所有回歸系數的相伴概率值Sig. ≤ 0.05。所得結果如表4所示，其中，只有變形模量E回歸分析中的節理抗拉強度σb未通過系數顯著性檢驗。

從表4中可以看出，宏觀參數擬合公式的R2值在0.881～0.996之間，說明擬合效果較好，能夠比較準確反映宏細觀參數之間的關系，其中，以變形模量E、單軸抗拉強度σf和抗拉強度σt的擬合效果相對較好，相關系數R2大于0.99；而內摩擦系數tanφ和內聚力C的擬合效果相對較差，說明兩者與細觀參數的關系較為復雜；泊松比回歸分析中入選的細觀參數最多，說明泊松比受到了多種因素的影響，與細觀參數之間的關系也比較復雜。雖然回歸分析的擬合效果參差不齊，但是這些公式可以定性地反映宏細觀參數之間的關系。對應的回歸系數為正，則說明細觀參數與宏觀參數之間呈正相關關系；對應的回歸系數為負，則說明細觀參數與宏觀參數之間具有負相關關系。

2.4 顆粒粒徑對宏觀性質的影響

上述分析中顆粒最小半徑Rmin = 0.5 mm，顆粒半徑比固定為1.66，在實際應用中，為了得到更好的模擬效果，我們可能會選擇更小的顆粒粒徑，這時候就需要考慮顆粒粒徑對宏觀參數的影響。分別選擇顆粒最小粒徑為0.50、0.45、0.40、0.35 mm，顆粒半徑比固定為1.66進行數值試驗，獲取宏觀參數。平直節理黏結顆粒材料的細觀參數選擇如表5所示，該細觀參數對應的宏觀參數滿足一般巖石力學性質對應的范圍。

圖7為宏觀參數相對于顆粒最小粒徑的變化曲線。從圖中可以看出，在細觀參數不變的情況下，顆粒粒徑的改變對試樣宏觀強度和變形性質的影響都比較小，僅內摩擦角和內聚力的變化幅度相對較大。上述結果表明，在一定范圍內，顆粒流模型宏觀性質受粒徑改變的影響較小。

3 巖石細觀參數標定方法

由于宏、細觀參數之間具有相關性，同樣類似于2.3節中的回歸分析，也可以建立細觀參數為因變量，宏觀參數為自變量的線性回歸表達式。這里采用逐步回歸法[15]，通過SPSS軟件實現，變量進入的概率門檻值為0.05，刪除的概率門檻值為0.10，擬合結果見表6。

從表6中可以看出擬合公式的相關系數R2在0.796～0.993之間，擬合效果良好。其中，平直節理剛度比和平直節理摩擦系數的擬合效果相對較差，說明宏細觀參數之間存在非線性關系。同時，根據表6中的結果，平直節理內摩擦系數tan φb未成功建立擬合表達式，從圖6中的多因素方差結果也可以看出，tan φb不是任何一個宏觀參數最顯著的影響因素，由此導致其不易確定。擬合公式中，黏聚力C也并未出現在自變量中，這說明黏聚力C與其他宏觀參數之間具有多重共線性。根據摩爾庫倫屈服準則可以得到C與σf、tan φb之間的關系[16]為

將表3中的宏觀參數σf和tan φ代入式（7）預測C值，并與表3中的C值進行對比，以此說明顆粒流模型是否能夠反映巖石宏觀參數之間的基本關系。對比結果如圖8所示，從中可以看出預測值與實際值之間相關系數達到了0.969 3，擬合關系式中系數1.048 2，非常接近于1，這說明顆粒流模型所反映的巖石宏觀參數之間的基本關系是符合實際的。

根據表6中的線性擬合公式，可以初步確定細觀參數，至于tan φb可取0.5作為初始值。此時，所確定的細觀參數只是初步估計，并不能準確反映宏觀性質，還需進行數值試驗計算宏觀參數，對比計算宏觀參數與實際宏觀參數之間的差別，再根據表4中擬合公式中所反映的宏細觀參數之間的趨勢性關系，可對細觀參數進行適當微調，直到達到合理的精度范圍。如果改變顆粒粒徑建立數值模型，則需要重新調整細觀參數，由于顆粒粒徑變化對巖石宏觀性質的影響并不大，可通過數值試驗對細觀參數進行適當微調。

4 實例分析

4.1 細觀參數的標定

采用焦作市龍寺廢棄礦山奧陶系中統上馬家溝組（O2s）厚層狀灰巖。每組試樣4個，在INSTORN-1346電液伺服巖石力學測試系統進行單軸壓縮和巴西劈裂試驗，取測試結果平均值，如表7所示。

由于未測試灰巖三軸強度參數，本文僅標定Ec、kn/ ks、σb、cb4個細觀參數，tan φb和μb統一取為0.5。在正交試驗時，本文采用直接拉伸試驗確定抗拉強度，而巖石試驗采用巴西劈裂試驗。數值模擬結果表明，直接拉伸的抗拉強度一般是平臺巴西劈裂抗拉強度的95%左右[11， 17]，對于本文的平直節理黏結顆粒材料，按表2數據經測算該系數平均為92%。因此，將巴西劈裂試驗所確定抗拉強度乘以系數92%即可采用表6中公式初步確定細觀參數。生成顆粒流試樣時，采用的空隙率為0.1，由此可以根據巖石密度確定顆粒密度，采用公式

ρs=ρ（1-r）（8）

式中：ρs為顆粒密度；ρ為巖石密度；r為數值試樣空隙率，取0.1。

將表7中宏觀參數（抗拉強度乘以系數92%）代入表6中的擬合公式初步確定細觀參數如表8所示。根據初步確定的細觀參數進行數值試驗可得宏觀參數的初步模擬值如表7所示，可以看出初步模擬值已經比較接近于實際值。對比初步模擬值與實際值之間的差別，再根據宏細觀參數之間的趨勢性關系進行微調，最終獲得精確估計的細觀參數如表8所示。對應的精確模擬值見表7，可以看出精確模擬值已經非常接近于實際值。由此說明本文方法是可行的。

4.2 數值模擬結果分析

4.2.1 試樣破壞對比

破壞試樣的對比如圖9、圖10所示。從圖中可以看出，數值模擬結果與巖石試驗結果是比較一致的。單軸壓縮下巖樣的破壞形態都主要表現為脆性劈裂破壞以及表層剝離；巴西劈裂下巖樣的破壞形態都主要表現為徑向的脆性劈裂破壞。

4.2.2 應力應變曲線對比

應力應變曲線的對比如圖11所示。從圖中可以看出，數值模擬和室內試驗所得應力應變曲線比較接近，都能體現灰巖的脆性破壞特征，但在曲線形態上存在一些差異。首先，顆粒流模擬結果沒有孔隙裂隙壓密階段，應力開始增加時，即出現彈性變形階段，這是由其建模原理所決定的；其次，單軸壓縮數值模擬的殘余強度接近于零，而實際巖石破壞后是存在一定的殘余強度的。由此可見，顆粒流模型可以得到接近于室內試驗的宏觀參數和應力應變曲線，但是仍然存在一些無法符合實際的問題，這是由數值模擬方法對實際復雜問題的簡化描述所決定的。

4.2.3 雙軸壓縮數值試驗

在已知三軸強度參數的情況下，可通過雙軸壓縮數值試驗對tan φb、μb兩個細觀參數進行標定。圖12是上述標定細觀參數對應的雙軸壓縮數值試驗模擬結果（位移圖）。從圖中可以看出，隨著圍壓的增大，數值試樣的破壞逐漸由徑向劈裂破壞轉變為剪切破壞，符合一般室內巖石試驗所得結果，采用摩爾庫倫屈服準則即可確定強度參數C、tan φb，若已知三軸強度參數，將其與數值模擬結果進行對比，可實現細觀參數的標定。

5 結 論

1）采用正交試驗設計、多因素方差分析和回歸分析研究了平直節理黏結顆粒材料宏細觀參數之間的關系，確定了宏觀參數的顯著性影響因素（細觀參數）及其排序，確定了宏細觀參數之間的相關關系。

2）建立了以細觀參數為因變量，宏觀參數為自變量的線性回歸表達式，由此提出了巖石細觀參數的標定方法，即以線性回歸表達式初步估計細觀參數，然后進行數值試驗對比計算宏觀參數與實際宏觀參數之間的差別，再根據宏細觀參數之間的趨勢性關系，對細觀參數進行適當微調，直到達到合理的精度范圍。

3）以灰巖的室內試驗結果為基礎，建立了灰巖的單軸壓縮和巴西劈裂數值模型，并對數值模型的細觀參數進行標定，模擬結果顯示顆粒流模型可以得到接近于室內試驗的宏觀參數和應力應變曲線，驗證了本文方法的有效性。

參考文獻：

[1] POTYONDY D O，CUNDALL P A.A bonded-particle model for rock [J].International Journal of Rock Mechanics and Mining Sciences，2004，41（8）：1329-1364.

[2] 夏明，趙崇斌.簇平行黏結模型中微觀參數對宏觀參數影響的量綱研究[J].巖石力學與工程學報，2014，33（2）：327-338.

XIA M，ZHAO C B. Dimensional analysis of effects of microscopic parameters on macroscopic parameters for clump parallel-bond model [J].Chinese Journal of Rock Mechanics and Engineering，2014，33（2）：327-338. （in Chinese）

[3] CHO N，MARTIN C D，SEGO D C.A clumped particle model for rock [J].International Journal of Rock Mechanics and Mining Sciences，2007，44（7）：997-1010.

[4] POTYONDY D O.A flat-jointed bonded-particle material for hard rock [C]// Proceedings of the 46th US Rock Mechanics Symposium，Chicago，2012：24-27.

[5] YOON J.Application of experimental design and optimization to PFC model calibration in uniaxial compression simulation [J].International Journal of Rock Mechanics & Mining Sciences，2007，44（6）：871-889.

[6] 顏敬，曾亞武，高睿，等.無黏結材料顆粒流模型的宏細觀參數關系研究[J].長江科學院院報，2012，29（5）：45-50.

YAN J，ZENG Y W，GAO R，et al.Relationship between macroscopic and mesoscopic parameters in particle flow model of unbounded material [J].Journal of Yangtze River Scientific Research Institute，2012，29（5）：45-50. （in Chinese）

[7] 周喻，吳順川，焦建津，等.基于BP神經網絡的巖土體細觀力學參數研究[J].巖土力學，2011，32（12）：3821-3826.

ZHOU Y，WU S C，JIAO J J，et al.Research on mesomechanical parameters of rock and soil mass based on BP neural network [J].Rock and Soil Mechanics，2011，32（12）：3821-3826. （in Chinese）

[8] 趙國彥，戴兵，馬馳.平行黏結模型中細觀參數對宏觀特性影響研究[J].巖石力學與工程學報，2012，31（7）：1491-1498.

ZHAO G Y，DAI B，MA C.Study of effects of microparameters on macroproperties for parallel bonded model [J].Chinese Journal of Rock Mechanics and Engineering，2012，31（7）：1491-1498. （in Chinese）

[9] 曾青冬，姚軍，霍吉東.基于并行 PSO算法的巖石細觀力學參數反演研究[J].西安石油大學學報（自然科學版），2015，30（4）：27-32.

ZENG Q D，YAO J，HUO J D.Inversion of rock meso-mechanical parameters based on parallel particle swarm optimization（PSO） algorithm [J].Journal of Xi'an Shiyou University （Natural Science Edition），2015，30（4）：27-32. （in Chinese）

[10] 叢宇，王在泉，鄭穎人，等.基于顆粒流原理的巖石類材料細觀參數的試驗研究[J].巖土工程學報，2015，37（6）：1031-1040.

CONG Y，WANG Z Q，ZHENG Y R，et al.Experimental study on microscopic parameters of brittle materials based on particle flow theory [J].Chinese Journal of Geotechnical Engineering，2015，37（6）：1031-1040. （in Chinese）

[11] 孟京京，曹平，張科，等. 基于顆粒流的平臺圓盤巴西劈裂和巖石抗拉強度[J]. 中南大學學報（自然科學版），2013，44（6）：2449-2454.

MENG J J，CAO P，ZHANG K，et al.Brazil split test of flattened disk and rock tensile strength using particle flow code [J]. Journal of Central South University （Science and Technology），2013，44（6）：2449-2454. （in Chinese）

[12] 張偉，韓旭，劉杰，等.一種基于正交試驗設計的土中爆炸數值模型確認方法[J].工程力學，2013，30（3）：58-65.

ZHANG W，HAN X，LIU J，et al.A method for model validation of underground explosion based on the orthogonal experimental design [J].Engineering Mechanics，2013，30（3）：58-65. （in Chinese）

[13] POULSENN B A，ADHIKARY D P.A numerical study of the scale effect in coal strength [J].International Journal of Rock Mechanics & Mining Sciences，2013，63：62-71.

[14] 譚海中，何波.基于多因素方差分析的文本向量特征挖掘算法[J].科技通報，2015，31（6）：139-141.

TAN H Z，HE B.Algorithm of text vectors feature mining based on multi factor analysis of variance [J].Bulletin of Science and Technology，2015，31（6）：139-141. （in Chinese）

[15] 范雯.逐步回歸分析方法在儲層參數預測中的應用[J].西安科技大學學報，2014，34（3）：350-355.

FAN W. Application of stepwise regression analysis method in reservoir parameter prediction [J].Journal of Xian University of Science and Technology，2014，34（3）：350-355. （in Chinese）

[16] 劉佑榮，唐輝明.巖體力學[M].北京：化學工業出版社，2008.

[17] 王啟智，賈學明.平臺巴西圓盤試樣確定脆性巖石的彈性模量、拉伸強度和斷裂韌度—第一部分：解析和數值結果[J].巖石力學與工程學報，2002，21（9）：1285-1289.

WANG Q Z，JIA X M.Determination of elastic modulus，tensile strength and fracture toughness of brittle rocks by using flattened Brazilian disk specimen-Part I：Analytical and numerical results [J].Chinese Journal of Rock Mechanics and Engineering，2002，21（9）：1285-1289. （in Chinese）

（編輯 王秀玲）