引潮位展開的不同規格化形式及其轉換

雷偉偉 張捍衛 孫 茜

1 河南理工大學測繪與國土信息工程學院，焦作市世紀大道2001號，454000

?

引潮位展開的不同規格化形式及其轉換

雷偉偉1張捍衛1孫 茜1

1 河南理工大學測繪與國土信息工程學院，焦作市世紀大道2001號，454000

在引潮位展開過程中，為使大地系數的數值在不同階次中保持相對穩定，對其進行規格化處理。從引潮位的基本理論公式出發，在分析締合勒讓德函數及其完全規格化的基礎上，給出了引潮位展開中3類不同規格化(Doodson規格化、Cartwright & Tayler規格化、Hartmann & Wenzel規格化)公式的具體形式，得到3者之間的轉換關系與轉換系數。同時給出Doodson規格化中2～6階規格化因子的具體數值，指出并改正Doodson、Roosbeek文獻和IERS 2003、2010規范中的3處錯誤。

完全規格化締合勒讓德函數；大地系數；潮波分量；規格化因子；IERS 規范

引潮位展開是地球物理、空間科學、天文/測地學研究的基本理論問題。Doodson[1]首先基于勒讓德函數和球面天文學的相關理論，通過對引潮位理論公式進行演繹推導，實施了引潮位的完全解析展開。Cartwright等[2]、Hartmann等[3]、Kudryavtsev[4]對引潮位的理論數值序列進行頻譜分析，得到潮波分量的頻率和振幅。在展開過程中，學者們均將引潮位統一表達為“大地系數”與“潮波分量”之積的形式，其中“大地系數”由兩部分組成，分別為測站地心緯度φ和測站地心距r的函數。各階次中與r相關的函數極值均約等于1，而與φ相關的函數極值變化甚大。為使“大地系數”的數值在不同階次中保持相對穩定，在各展開過程中都對“大地系數”進行了規格化處理。規格化方法主要有3類：Doodson規格化、Cartwright & Tayler規格化、Hartmann & Wenzel規格化。

郗欽文[5]研究了前兩類規格化之間的轉換關系，給出了2～4階的Doodson規格化因子與轉換系數的具體數值。IERS規范[6-7]給出了2～3階的各規格化之間的轉換參數，但個別參數有誤。這些轉換參數都是通過對“大地系數”各階次的具體展開式進行比對后得出的，并未從理論層面揭示出轉換參數的內在實質。本文擬從引潮位展開的理論公式出發，通過對3類規格化方法本質的描述，揭示3類方法間的內在關系，并給出轉換參數的一般化公式形式。

1 理論公式

某歷元天體對地面某測站點總的引潮位V為[8]：

(1)

式中，GMJ為萬有引力常數與天體J的質量之積，RJ、r分別表示天體、測站點的地心距，ZJ為天體與測站之間的地心天頂距：

cosZJ=sinφsinδJ+cosφcosδJcosHJ

(2)

(3)

式中，(αJ,δJ)、(λ,φ)分別表示天體、測站點在地心參考系中的地心經度、地心緯度，HJ為天體的地方時角。

2 各規格化公式

2.1 Doodson規格化公式及其展開式

定義Doodson常數DJ為：

(4)

式中，a為地球參考橢球長半徑，cJ為天體J到地球的平均地心距。

將式(1)改寫為：

(5)

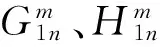
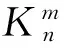
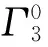
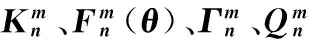
表1 2～6階的

2.2 Hartmann & Wenzel規格化公式及其展開式

由文獻[9]可知：

Pn(cosZJ)=

(6)

故文獻[3]將式(1)表達為如下形式：

(7)

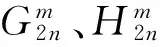
2.3 Cartwright & Tayler規格化公式及其展開式

(8)

并將式(1)改寫為：

(9)

3 各規格化公式之間的轉換

3.1 Doodson規格化與Hartmann & Wenzel規格化之間的轉換

將式(7)改寫為：

(10)

(11)

因此，Doodson規格化與Hartmann & Wenzel規格化之間的轉換關系為：

(12)

式(5)是將式(2)代入Pn(cosZJ)展開式后合并同類項得到的。事實上，根據式(6)，Doodson規格化公式的本質為：

(13)

3.2 Hartmann & Wenzel規格化與Cartwright & Tayler規格化之間的轉換

將式(8)改寫為：

(14)

將式(9)改寫為：

(15)

對比式(7)與式(15)，即可得到Cartwright & Tayler規格化與Hartmann & Wenzel規格化之間的轉換關系：

(16)

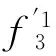
3.3 Doodson規格化與Cartwright & Tayler規格化之間的轉換

將式(15)繼續改寫為：

(17)

對比式(13)與式(17)即可得到Doodson規格化與Cartwright & Tayler規格化之間的轉換關系：

(18)

該轉換關系也可以通過式(12)、式(16)間接得到：

(19)

4 結 語

在引潮位展開中存在Doodson規格化、Cartwright & Tayler規格化、Hartmann & Wenzel規格化3類不同的規格化方法。郗欽文[5]給出了Doodson規格化與Hartmann & Wenzel規格化之間的轉換關系，并給出了2～4階的Doodson規格化因子與轉換系數的具體數值。本文是對郗欽文[5]工作的擴展，不僅給出了引潮位展開中3類不同規格化公式的具體形式，還由此得到3類不同規格化方法之間的轉換關系與轉換系數。同時給出了Doodson規格化中2～6階規格化因子與轉換系數的具體數值，指出并改正文獻[10]和IERS規范[6-7]中的兩處錯誤。

[1] Doodson A T. The Harmonic Development of the Tide-Generating Potential [J]. Proceedings of the Royal Society of London A: Mathematical, Physical and Engineering Sciences, 1921, 100(704): 305-329

[2] Cartwright D E, Tayler R J. New Computations of the Tide-Generating Potential [J]. The Geophysical Journal of the Royal Astronomical Society, 1971, 23(1): 45-74

[3] Hartmann T, Wenzel H G. The HW95 Tidal Potential Catalogue [J]. Geophysical Research Letters, 1995, 22(24): 3 553-3 556

[4] Kudryavtsev S M. Improved Harmonic Development of the Earth Tide Generating Potential [J]. Journal of Geodesy, 2004, 77(12): 829-838

[5] 郗欽文. 不同規格化的引潮位展開及其轉換[J]. 地球物理學報，2007, 50(1): 111-114(Xi Qinwen. Expansion of the Tidal Generating Potential in Different Normalizations and Their Convention [J]. Chinese Journal of Geophysics, 2007, 50(1): 111-114)

[6] McCarthy D D, Petit G. IERS Conventions (2003), IERS Technical Note 32 [R]. Frankfurt am Main: Verlag des Bundesamts für Kartographie und Geod?sie, 2003

[7] Petit G, Luzum B. IERS Conventions (2010), IERS Technical Note 36 [R]. Frankfurt am Main: Verlag des Bundesamts für Kartographie und Geod?sie, 2010

[8] Melchior P. The Tides of the Planet Earth[M].Oxford:Pergamon Press, 1983

[9] Hofmann W B, Moritz H. Physical Geodesy [M]. NewYork:Springer, 2006

[10]Roosbeek F. RATGP95: A Harmonic Development of the Tide-Generating Potential Using an Analytical Method [J]. Geophysical Journal, 1996, 126(1): 197-204

About the first author:LEI Weiwei, lecturer, PhD candidate, majors in geodesy, E-mail: geodesy@163.com.

The Different Normalization Forms of Tidal Generating Potential Development and Their Transformation

LEIWeiwei1ZHANGHanwei1SUNQian1

1 School of Geodesy and Land Information Engineering, Henan Polytechnic University, 2001 Shiji Road, Jiaozuo 454000, China

In the Tidal Generating Potential (TGP) development process, the geodetic coefficient is normalized in order to maintain the relative stability of its value among different degrees and orders. At present, there are three main normalization methods: Doodson normalization, Cartwright & Tayle normalization, and Hartmann & Wenzel normalization. The specific formulas of these normalization methods in TGP development are derived from the basic theoretical formula of TGP, along with analysis of the associated Legendre’s functions and their full normalization forms. On this basis, the transformation relationships and coefficients among the three methods are obtained. At the same time, the specific values of the 2～6 degree and order normalization factors in Doodson normalization are given, while three errors in the treatise of Doodson and Roosbeek and in the IERS 2003,2010 Conventions are pointed out and corrected.

fully normalized associated Legendre functions; geodetic coefficient; tidal wave component; normalization factor; IERS conventions

National Natural Science Foundation of China, No.41474021; Surveying and Mapping Basic Research Program of NASMG, No.15-01-05.

2016-01-11

項目來源：國家自然科學基金(41474021)；國家測繪地理信息局測繪基礎研究基金(15-01-05)。

雷偉偉，講師，博士生，主要從事大地測量學研究，E-mail: geodesy@163.com。

10.14075/j.jgg.2016.12.016

1671-5942(2016)012-1105-04

P223

A