用MDMC-HS-tree方法計算極小碰集*

佘曉娓， 趙相福

(浙江師范大學 數理與信息工程學院,浙江 金華 321004)

?

用MDMC-HS-tree方法計算極小碰集*

佘曉娓， 趙相福

(浙江師范大學 數理與信息工程學院,浙江 金華 321004)

產生待診斷設備沖突集的所有極小碰集是基于模型診斷的一個重要步驟，極小碰集即為該設備的候選診斷.HS-tree算法產生的節點數目較多，效率較低.因此，提出了基于極大度和極小勢的MDMC-HS-tree方法.每次選擇勢最小的集合進行擴展，以便減小樹的寬度；并刪減包含勢最小集合中度最大元素的集合，不斷將大問題化簡為小問題.實驗結果表明：本算法能夠產生所有極小碰集，且在計算大規模碰集時產生相對較少的節點，為實際設備故障診斷提供較可行的方法.

極小碰集；基于模型診斷；極大度；極小勢；碰集樹

0 引 言

早前的專家系統診斷方法是一個依靠經驗知識并基于啟發式規則的診斷過程[1].為克服傳統專家診斷在系統規模增大時造成不完備和長時間推理過程的不足，人們引入了關于系統的功能、結構、行為等方面的知識，提出了基于模型的診斷[2].基于模型診斷是人工智能的重要領域，主要具有以下優點[3]：1)可以發現系統設計者不可預見的故障；2)具有可重用和易于維護的模型；3)獲取知識相對比較容易；4)具有較強的解釋能力；5)獨立性較強.在基于模型的診斷中，當觀察的行為與系統預測的行為發生矛盾時，說明系統中有存在故障的部件，邏輯推導得出引發故障的部件集合(極小沖突集)[4].極小碰集是由系統的極小沖突集計算得出，這些極小碰集即為系統的候選診斷.因此，在基于模型診斷中，求解極小碰集是關鍵步驟之一.

目前，計算極小碰集的算法有很多，其中最早且最經典的HS-tree[5]算法是由著名的人工智能專家Reiter在1987年提出.但在HS-tree算法計算極小碰集時剪枝過程繁瑣，在某些情況下會因為剪枝而丟失正確解，且產生的節點較多，不適用于大型系統.奧地利學者Wotawa對HS-tree算法進行改進，提出了HST-tree[6]算法.此后，在HS-tree算法的基礎上提出了BHS-tree[7]、HSSE-tree[8]、CHS-tree[9]和DMDSE-tree[10]等計算極小碰集的算法.

然而，以上這些方法存在著某些不足：1)計算過程中有可能會丟失正確解；2)節點數目比較多，存儲比較復雜；3)先存儲計算得到的碰集，需要去掉超集以得到正確的極小碰集.

本文針對上述缺點，提出了新的求解極小碰集的方法，此方法是對基于極小勢計算極小碰集算法的改進，并結合極大度來求解極小碰集.本算法的主要優點有：

1)在求解過程中，每次選擇勢最小的集合進行擴展，縮小樹的寬度；

2)按擴展節點中元素度的大小，順序地刪除集合中含有該元素的集合，直到集合為空，這樣就縮小了樹的深度，盡早生成極小碰集，減少節點個數；

3)通過添加終止節點與對相關集合的化簡，避免產生更多的非極小碰集；

4)此方法不會丟失正確的解，這是因為無需對生成樹進行剪枝.

1 基本原理

以下將對算法的相關概念及定理進行闡述.

定義1[5]將系統定義為一個三元組(SD,COMPS,OBS)：

1)SD為描述系統的相關行為的一階謂詞集合，包含診斷中的關鍵信息；

2)COMPS系統中所有的部件是一組有限的常量集，例如：系統的組件集用常量集合{c1,c2,c3,…,cn}表示；

3)OBS表示系統的觀測值，是用一階謂詞公式表示的有限集合.

在待診斷的設備中，若設備的行為描述與觀測值之間存在矛盾，則表明該設備的某個部件存在故障，通常使用一元謂詞AB(5)表示“abnormal”，當且僅當c出現故障時，AB(c)為真，其中c∈COMPS.

定義2[5]有一部件集{c1,c2,…,cn}是沖突集(CS)，且{c1,c2,…,cn}?COMPS，使SD∪OBS∪{～AB(c1),～AB(c2),…,～AB(cn)}出現矛盾，說明系統中有部件存在故障，則此時的元件集{c1,c2,…,cn}是該系統的沖突集CS.

假設有一沖突集{c1,c2,c3}是極小沖突集，當且僅當{c1,c2,c3}的所有真子集都不是沖突集，則稱該沖突集為極小沖突集(MCS).

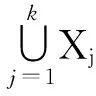
給定一個碰集H，若它的任意真子集都不是F的碰集，則稱H是集合簇F的極小碰集，也可用MHS(F)表示.

定義4[9]元素c覆蓋集合S，當且僅當c∈S.稱元素覆蓋集合簇F中集合的個數為該元素的度(degree).集合S={b1,b2,…,bn}的度為集合中各個元素的度數和.

例1 集合簇F={{a,b}，{b,c}，{a,c}}，元素a的度為2，元素b的度為2，元素c的度為2，則集合S={a,b}的度為元素a和元素b的度之和，即為4.

在描述本文算法之前，對基于極小勢求解極小碰集的相關概念進行介紹.

定義5[10]給定集合S={b1,b2,…,bn}，用集合的勢(Cardinality)表示元素的個數.

例如，集合S的勢為n.集合規模的大小用集合的勢來衡量.

定義6[4]若集合X1和X2滿足X2?X1，則稱X1為X2的真超集.

例2 設X1={1,3,5}，X2={3,5}，則X1是X2的真超集.

命題1[4]給定一個非空集合簇F，若存在2個集合X，X′∈F，并且X?X′，則MHS(F-{X′})=MHS(F)，即F-{X′}與F有相同的極小碰集.

例3 集合簇F={{1,2}，{1,3,4}，{3,4}}，集合X={3,4}，X′={1,3,4}.則F-{X′}={{1,2}，{3,4}}，F的所有極小碰集為：{1,3}，{1,4}，{2,3}，{2,4}；F-{X′}的所有極小碰集同樣為：{1,3}，{1,4}，{2,3}，{2,4}.

顯然，假設有2個非空集合簇F和F′，且F′?F，則集合簇F與集合簇F′有相同的碰集.

2 MDMC-HS-tree算法計算極小碰集

2.1 CHS-tree算法描述

下面對CHS-tree算法進行簡述.CHS-tree算法的步驟如下：

步驟1：化簡集合簇F，去掉集合的真超集，保證F是極小沖突集簇.

步驟2：計算集合簇F中集合的勢，找到勢最小的集合進行擴展.對于極小勢相同的幾個集合，找出元素出現頻率最大的集合作為擴展節點.

步驟3：依次刪除集合簇F中包含待擴展集合CS={a1,a2,a3,…,am}中元素的集合，返回步驟1，直到F變為空集.

步驟4：自頂向下進行遍歷，從根節點到葉節點的每條路徑即為一個碰集，并對其化簡(去掉真超集)，得到極小碰集.

例4 給定一個集合簇F={{1,3,5}，{3,4,5}，{2,5}，{5,6,7}，{3,7,8}}，計算F的所有極小碰集為：{3,5}，{5,7}，{5,8}，{1,2,4,7}，{1,2,4,6,8}，{2,3,6}，{2,3,7}.用基于極小勢計算極小碰集的CHS-tree算法，其過程如圖1所示.

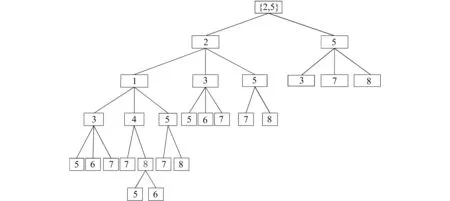
圖1 沖突集簇為{{1,3,5}，{3,4,5}，{2,5}，{5,6,7}，{3,7,8}}時的CHS-tree算法

可以看出，用CHS-tree計算極小碰集時，在樹的左子樹中依然會產生較多極小碰集的真超集，從而節點的數目有所增加.

2.2MDMC-HS-tree算法的基本步驟

從上述算法中可以看出，CHS-tree算法極大地改善了因剪枝丟失解的問題，但還會產生較多的節點.為了解決計算過程中節點數目較多的問題，本文結合CHS-tree算法和極大度的概念，并對其進行改進,得到一種產生節點較少的計算碰集的方法，即MDMC-HS-tree算法.

MDMC-HS-tree算法的步驟如下所述：

步驟1：化簡集合簇F，將集合簇F中的真超集去掉;

步驟2：計算F中集合的勢和F中元素的度，找到集合簇F中勢最小的集合(若勢相同則選擇集合度最大的集合)按深度優先的原則進行擴展;

步驟3：假設待擴展集合為CS={a1,a2,a3,…,am}，對集合中的元素的度進行比較，并假設degree(a1)>degree(a2)>…>degree(am).先刪除F中包含a1(元素的度最大)的集合，返回步驟1，直到集合簇F為空集，…，刪除F中包含am的集合，返回步驟1，直到集合簇F為空集;

步驟4：自頂向下進行遍歷，從根節點到葉節點每條路徑上的元素構成的集合即為一個碰集.

詳細復雜性分析如下：

1)在擴展節點前首先刪除集合簇的真超集，可以減少節點數目及循環次數.

2)從集合的極小勢出發，可以減小樹的寬度，從而減少節點數目.

3)按深度優先的原則刪除包含待擴展節點集合中元素的集合，使得要考慮的集合不斷減少，進而使樹的深度減少.

4)在刪除包含待擴展節點集合中元素的集合時應首先考慮刪除包含度最大元素的集合，這樣刪除的集合就會更多，最后刪除度最小的元素，直到沖突集簇為空集.

5)MDMC-HS-tree算法的復雜度與產生節點的數目有關.通過刪除沖突集簇中的真超集，使得沖突集簇集合數目減少.在擴展的過程中，樹的深度不斷減小.這是由于在刪除集合過程中，根據集合元素度的大小順序地刪除與節點相關聯的集合，使集合簇F中集合個數不斷減少；另外,樹的寬度因通過刪除同一層中已經出現過的終止節點的元素而變小.根據這2個方面，可以減少節點數目.

3 實例執行及驗證結果

基于上述提出的基于極大度和極小勢的MDMC-HS-tree求解碰集方法及過程，舉例分析如下：

例5 仍然考慮例4中的沖突集簇F={{1,3,5}，{3,4,5}，{2,5}，{5,6,7}，{3,7,8}}，使用MDMC-HS-tree方法求解所有極小碰集.具體步驟如下：

1)先去掉集合簇F中的真超集,得到集合簇F′={{1,3,5}，{3,4,5}，{2,5}，{5,6,7}，{3,7,8}}.

2)找出F′中勢最小的集合{2,5}，對集合{2,5}進行擴展.

3)統計集合中的元素2，5的度分別為1，4，先刪除F′中包含元素5的集合，得到集合簇F1={{3,7,8}}，選擇集合{3,7,8}進行擴展.

4)集合{3,7,8}元素的度分別為1，1，1，將F1中包含元素3的集合刪除，F1為空，3為終止節點；將F1中包含元素7的集合刪除，F1為空，7為終止節點；刪除包含元素8的集合，F1為空，8為終止節點.

5)①刪除F′中包含2的集合，集合簇變為F2={{1,3,5}，{3,4,5}，{5,6,7}，{3,7,8}}，同時將集合簇F2中的元素5刪除(包含5的碰集已經求解完畢)，刪除元素5后的集合為F2={{1,3}，{3,4}，{6,7}，{3,7,8}}.

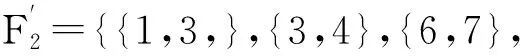
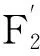
④刪除元素6，集合為空，6為終止節點;刪除元素7，集合為空，7為終止節點.

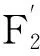
②選擇集合{6,7}進行擴展，刪除元素7(7的度為2)，集合為空，7為終止節點.

③刪除元素6，剩下集合為{7,8}，刪除同層元素7，剩下的集合為{8}，刪除元素8，集合為空，則8為終止節點.

7)從根節點到葉節點進行遍歷，每條路徑上的元素構成一個集合，最終得到極小碰集為{3,5}，{5,7}，{5,8}，{1,2,4,7}，{1,2,4,6,8}，{2,3,6}，{2,3,7}.

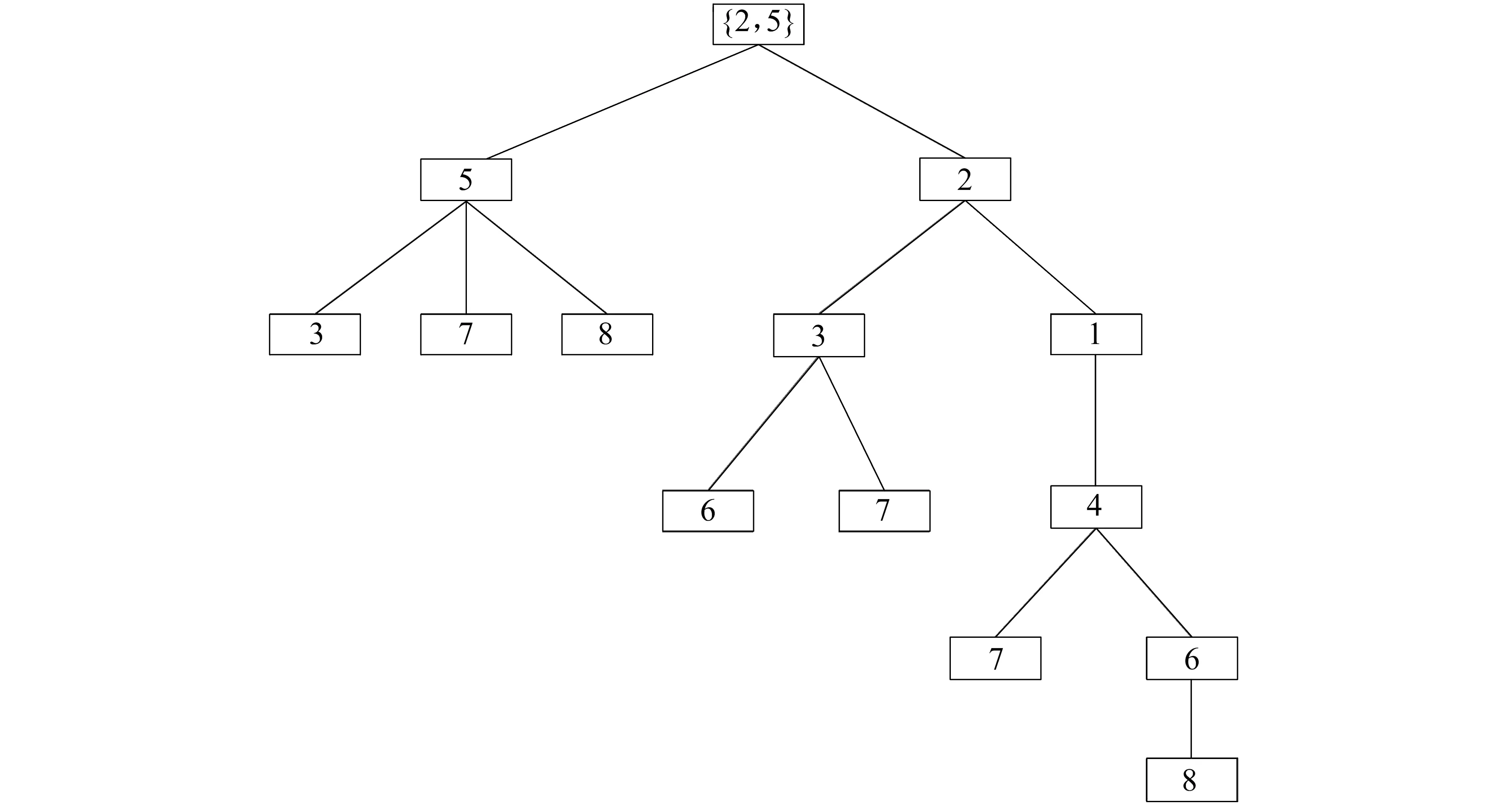
圖2 沖突集為{{1,3,5}，{3,4,5}，{2,5}，{5,6,7}，{3,7,8}}的MDMC-HS-tree算法

從圖2可以看出，勢最小的集合是{2,5}，對極小沖突集進行擴展，左子樹產生包含元素5的碰集，右子樹產生包含元素2的碰集.在產生包含元素2的碰集時，首先刪除元素5，從而保證不再產生包含元素5的碰集，包含元素5的碰集已在左子樹產生，避免產生更多的超集.按照深度優先原則擴展時，若集合中包含同一層出現過的終止節點，則將該元素從集合中刪除，這樣使樹的寬度減小，節點數目減少.

4 相關算法的比較

4.1 MDMC-HS-tree算法與CHS-tree算法的比較

從CHS-tree算法計算極小碰集的例子中可以看出，本文闡述的計算碰集的方法(MDMC-HS-tree)產生的節點少于CHS-tree算法得到的節點.集合之間關聯的元素越多，產生的節點相對越少.CHS-tree算法是基于極小勢求解極小碰集的方法，擴展集合的勢越小，樹的寬度就越小.本文提出的MDMC-HS-tree求解極小碰集的算法,延續了選擇勢最小的集合進行擴展的做法，同時考慮到集合與元素的度，集合的度越大，說明與這個集合中元素關聯的集合越多.MDMC-HS-tree算法產生的節點相對較少，這是由于在擴展的過程中，關聯的集合越多，刪除的集合更多，考慮的集合數目就越少.同時,在刪除擴展節點中的元素得到新的集合時，首先刪除度最大的元素，可以盡量減少真超集的產生，減少節點數目，從而減少刪除真超集的過程.本文算法的時間復雜度和空間復雜度主要跟元素的度、集合的勢有關，集合關聯數目越多，產生節點越少，時間和空間復雜度將會更小.

4.2 統計分析

為了對這些算法進行更進一步的比較，采用VisualC++6.0編程實現了MDMC-HS-tree算法，并在Intel(R) Core(TM) i5-6200U CPU @2.30GHz 2.40 GHz，4.00GB，Windows 10操作系統下運行，分別比較BHS-tree,HSSE-tree和CHS-tree方法計算極小碰集的效率，結果如圖3所示.沖突集個數為n=6，集合簇為{{1,2,3,…,m-1}，{2,3,4,…,m}，…,{n,n+1,…,n+m-2}}，m為沖突集元素個數.

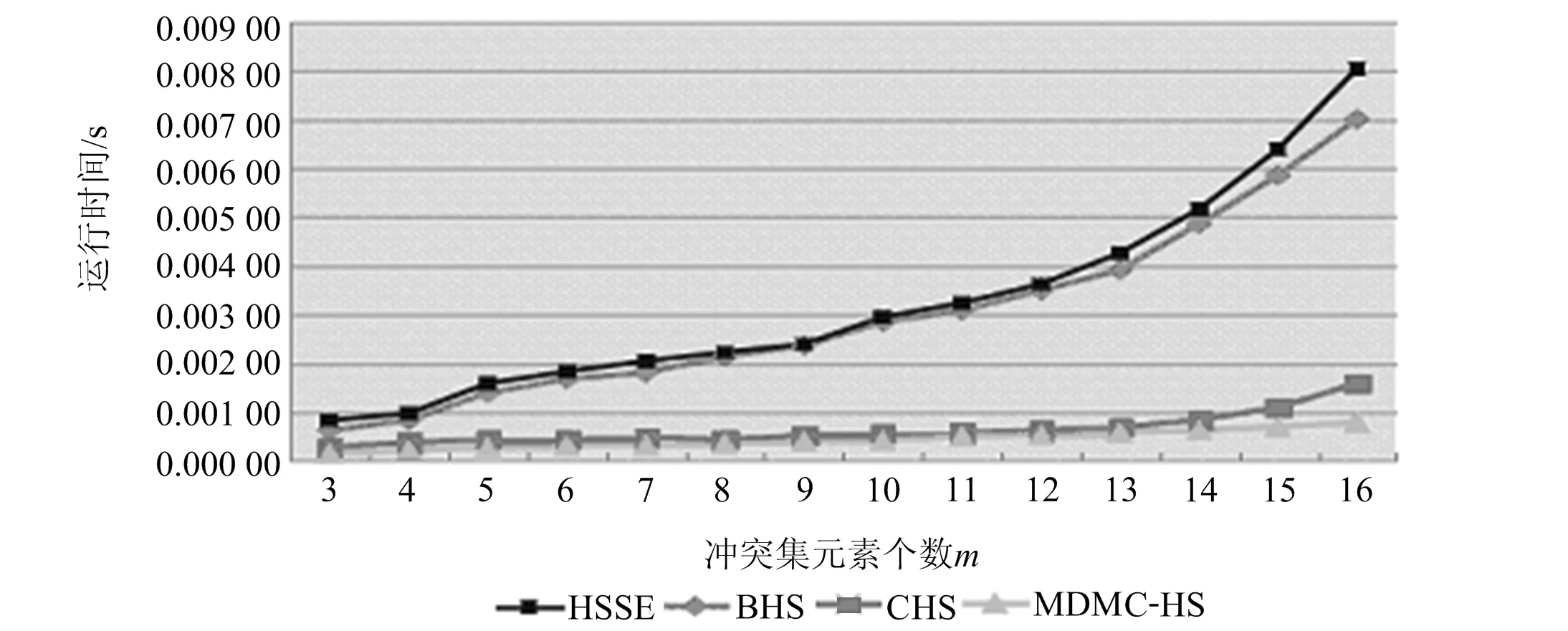
圖3 BHS-tree,HSSE-tree,CHS-tree和MDMC-HS-tree算法運行時間比較

從圖3可以看出，相對于BHS-tree,HSSE-tree和CHS-tree算法，本文提出的MDMC-HS-tree算法的運行效率明顯提高，隨著集合中元素個數的增加，其他3種算法的運行時間成倍增加.HSSE-tree和BHS-tree算法在元素個數增加時，運行時間已經比MDMC-HS-tree算法的運行時間高出4倍.

在沖突集合簇中每個集合的元素不是很多的情況下，CHS-tree算法與MDMC-HS-tree算法的運行時間差不多，但隨著元素個數的增加，集合中關聯的元素個數也在增多，MDMC-HS-tree算法明顯比CHS-tree算法運行時間少.

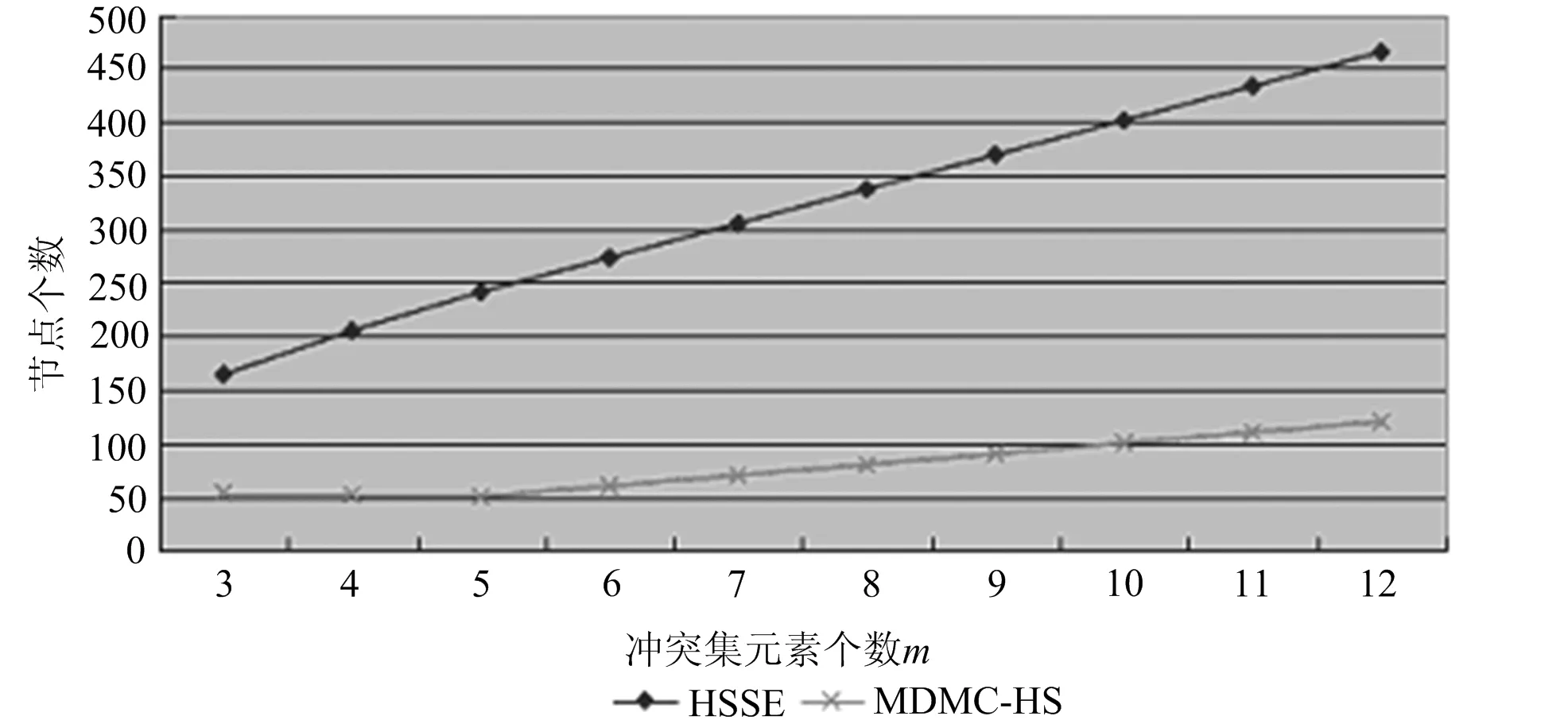
圖4 HSSE-tree和MDMC-HS-tree算法產生節點個數比較

此外，從圖4可以看出，HSSE-tree算法隨著沖突集中元素個數增多，節點的個數也在不斷增加，而MDMC-HS-tree算法的節點個數相對較少.

說明：

1)HSSE-tree算法在計算極小碰集前沒有刪除沖突集簇中的真超集，導致節點數目增加，而MDMC-HS-tree算法在執行前就將真超集刪除，在節點的擴展中減少了集合的數量，也避免產生更多極小碰集的真超集.

2)集合個數和沖突集的元素個數會影響生成樹中節點數目，若沖突集中關聯的元素較多，則MDMC-HS-tree算法產生的節點個數就相對較少.

3)MDMC-HS-tree算法在計算極小碰集時需要計算各集合中每個元素的度，按照選中集合中元素度的大小順序進行擴展，在接下來的擴展過程中會刪掉更多的集合.首先產生極小碰集，接著將會產生較少的真超集.相對CHS-tree算法，MDMC-HS-tree算法減少了刪除真超集的運算時間，并且減少節點的產生.例如：F={{1,2,3}，{2,3,4}，{3,4,5}}，CHS-tree算法產生7個節點，而MDMC-HS-tree算法只產生6個節點.

4)CHS-tree算法與MDMC-HS-tree算法在某些情況下產生的節點數目是相同的.例如，當極小沖突集簇為F={{1}，{2}，{3}，{4}}時，CHS-tree算法和MDMC-HS-tree算法都有4個節點，HSSE-tree算法有5個節點；若選中的極小沖突集中元素的度相等，則CHS-tree算法與MDMC-HS-tree算法產生的節點個數相同.例如，當極小沖突集簇F={{1,2}，{2,3}，{3,4}}時，CHS-tree算法與MDMC-HS-tree算法產生的節點個數都是5，而HSSE-tree算法產生13個節點.

綜上所述，MDMC-HS-tree算法結合了CHS-tree極小勢和集合度來求解極小碰集，在空間復雜度和時間復雜性上比較好，能有效地在實際系統中進行診斷.

5 結 語

實驗結果表明，MDMC-HS-tree算法是一種基于極大度和極小勢求解極小碰集的算法，在進行較大規模計算碰集時具有明顯優勢：通過建立樹型結構計算極小碰集，將大問題分解成小問題；與集合元素度相結合，減少樹的深度，減少節點的產生；不需要對樹進行剪枝，不會丟失極小碰集.在已知極小沖突集求解極小碰集的情況下，本文提出的算法效率較高，但有時所得診斷仍不能滿足實際要求，為了解決這個問題，需要增加更多的探測，根據得到的新沖突集計算新的極小碰集.筆者下一步將本文的方法進一步擴展至求解動態變化的極小沖突集的極小碰集，更有效地應用于實際系統中.

[1]韓旭，史忠值，林芬．基于模型診斷的研究進展[J]．高技術通訊，2009，19(5)：543-550.

[2]De Kleer J.Hitting set algorithms for model-based diagnosis[C]//Proceedings of the 22ed International Workshop on Principles of Diagnosis,Murnau:TU München;OCC′M Software GmbH;UMIT Hall/Tyrol,2011:100-105.

[3]Chittaro L,Guida G,Tasso C.Functional and teleological knowledge in the multimodeling approach for reasoning about physical systems[J].IEEE Transactions on Systems,Man and Cybernetics,1993,23(6):1718-1751.

[4]Davis R.Diagnostic reasoning based on structure and behavior[J].Artificial Intelligence,1984,24(1/2/3):347-410.

[5]Reiter R.A theory of diagnosis from first principles[J].Artificial Intelligence,1987,32(1):57-96.

[6]Wotawa F.A variant of Reiter′s hitting-set algorithm[J].Information Processing Letters,2001,79(1):45-51.

[7]姜云飛，林笠．用對分HS-樹計算最小碰集[J]．軟件學報，2002，13(12)：2267-2274.

[8]Zhao Xiangfu,Ouyang Dantong.A method of combing SE-tree to compute all minimal hitting sets[J].Progress in Nature Science,2006,16(2):169-174.

[9]張立明，歐陽丹彤，曾海林．基于動態極大度的極小碰集求解方法[J]．計算機研究與發展，2011，48(2)：209-215.

[10]王肖，趙相福．用CHS-tree基于集合勢的方法計算極小碰集[J]．計算機集成制造系統，2014，20(2)：401-406.

[11]歐陽丹彤，歐陽繼紅，劉大有．基于模型診斷的研究與新進展[J]．吉林大學自然科學學報，2001(2)：38-45.

[12]歐陽丹彤，張立明，趙劍，等．利用標志傳播求解基于模型的故障診斷[J]．儀器儀表學報，2011，32(12)：2857-2862.

[13]黃杰，陳琳，鄒鵬．一種求解極小診斷的遺傳模擬退火算[J].軟件學報，2004，15(9)：1345-1350.

[14]Han B,Lee S.Deriving minimal conflict sets by CS-tree with mark set in diagnosis from first principles[J].IEEE Transactions on System,Man and Cybernetics-Part B:Cybernetics,1999,29(2):281-286.

[15]林笠．基于模型診斷中用邏輯數組計算最小碰集[J]．暨南大學學報：自然科學與醫學版，2002，23(1)：24-27.

(責任編輯 陶立方)

On computing the minimal hitting sets by MDMC-HS-tree

SHE Xiaowei, ZHAO Xiangfu

(CollegeofMathematics,PhysicsandInformationEngineering,ZhejiangNormalUniversity,Jinhua321004,China)

Computing minimal hitting-sets (MHSes) based on all conflicts was an important step in model-based diagnosis. Reiter first proposed the HS-tree algorithm for computing MHSes. Generally, a large number of nodes were generated in an HS-tree. In order to improve the algorithm, a method of MDMC-HS-tree(Max-Degree-Min-Cardinality-based Hitting-Sets-tree) was proposed to compute MHSes for all conflict sets. Firstly, the set with minimal cardinality was selected from the current conflict set cluster to be expanded, so as to reduce the width of the tree. Then, the largest degree element in the minimal cardinality set was chosen to reduce current conflict set cluster. Experimental results showed that the algorithm generated all MHSes and produced a smaller number of nodes even for a large number of conflict sets. The algorithm was feasible for computing all MHSes in model-based diagnosis.

minimal hitting set; model-based diagnosis; max degree; minimal cardinality; HS-tree

10.16218/j.issn.1001-5051.2016.04.007

2016-01-15；

2016-03-19

國家自然科學基金資助項目(61003101);浙江省自然科學基金資助項目(LY16F020004;Y1100191)

佘曉娓(1991-),女，安徽黃山人，碩士研究生.研究方向：基于模型的故障診斷.

趙相福.E-mail： xiangfuzhao@gmail.com

TP31

A

1001-5051(2016)04-0399-07