基于分形的自然景物模擬及仿真
牛亞群
太原學院基礎部(太原 030032)
基于分形的自然景物模擬及仿真
牛亞群
太原學院基礎部(太原 030032)
介紹了分形理論的發展過程,闡述了迭代函數系統(IFS)的基本原理。利用IFS隨機迭代算法,采用Matlab軟件仿真,較好的模擬了自然景物,驗證了分形幾何理論。
分形理論;迭代函數系統;Matlab軟件仿真;自然景物模擬
分形理論是一種數學抽象,是自然界和社會的生活生產過程中的不完全規則事物高度概括。20世紀70年代,分形理論被首次提出,隨著周邊學科如計算機技術、網絡技術、計算機圖形學的成熟,已經成為一門重要的新學科,在很多應用領域得到很好的驗證和推廣,成為當今國際上許多學科的前沿研究課題之一。
分形理論在很多的基礎學科和交叉學科領域有了很重大的突破,對促進整體科學技術的推進和發展,促進學科融合起著重要的作用。
隨著計算機軟硬件技術的提升,分形理論很好的應用到了計算機對現實世界的模擬,尤其在不規則事物模擬上有了很大的突破。過去很多受到計算機內存、CPU和顯卡條件限制的分形理論實驗隨著計算機軟硬件設備的不斷攀登和發展均得到了長足進展。因此,本文以自然景物模擬為切入點,開展分形理論的實驗研究。
1 分形理論
1975年,美籍法國數學家Mandelbrot最先創用了分形理論。他通過這個詞來描述一大類復雜不規則的幾何對象。分形(fractal)一詞源于拉丁文fractus,本意是指“破碎的”、“產生不規則碎片”、“分數”等。分形理論目前還沒有嚴格的數學定義,只能給出描述性的概念。粗略的說,分形是沒有明確特征標度大自然本身描繪的曲線,其自相似性是統計數據抽象得來,并且,自相似性只存在于“無標度區間”[1]。
1904年,VonKoch通過初等方法構造了Von Koch曲線。該曲線的性質的最主要特征是處處不可微,該曲線是第一個發現的人為構造的局部與整體相似結構的曲線[2]。
得到Von Koch曲線的步驟如下:
設B0是平面A上的單位線段,將B0三等分。利用中間的1/3線段做出正三角形,新生成其他兩個邊。此時得到一個由4個長度為1/3的邊所組成的連續折線,稱此折線為B1,并稱B1是由B0繁衍生成的.
分別對B1的每一條邊都進行步驟1定義的規則變化,變化完成后可以得到由42個長度為1/32的邊組成的連續折線,記其為B2。
按照規則逐次迭代,可以從折線序列B0,B1,B2,...,Bn,得到有限精度的極限曲線,即為Von Koch曲線。
如下圖1所示即為Von Koch曲線的迭代過程。
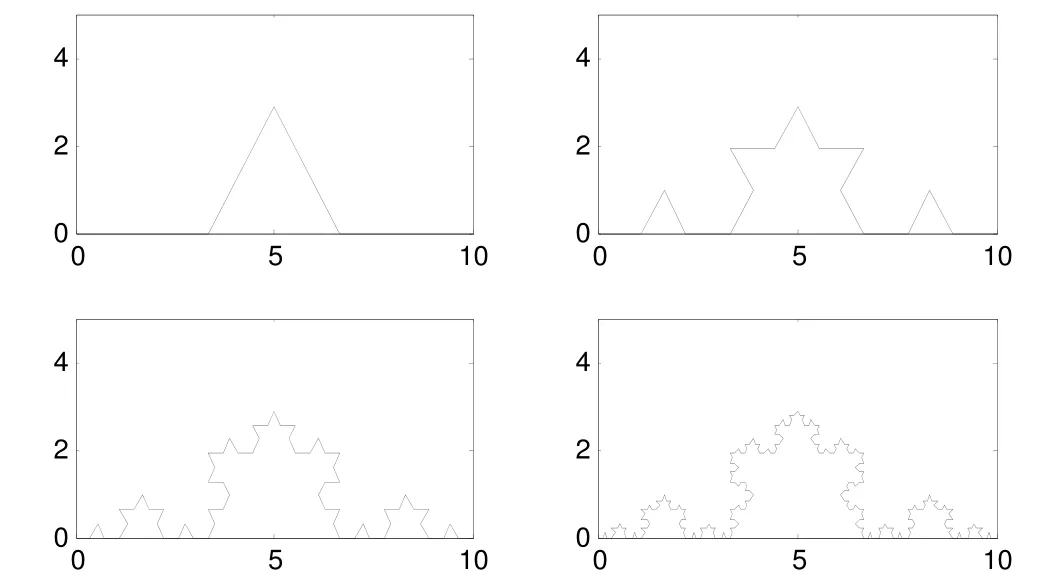
圖1 逐步迭代的Von Koch曲線
2 線性IFS隨機迭代算法
迭代函數系統又稱為線性迭代表達式,函數系統中的每個迭代函數表達式都是線性的。在線性迭代函數的迭代中,采用如下的迭代算法:
(1)設定一個起始點(x0,y0)及總的迭代步數;
(2)以概率pk(k=1,2,3,…,N)選取仿射變換Wk,Wk形式為:
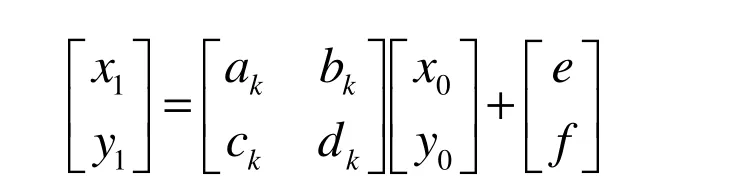
(3)以Wk作用點(x0,y0),得到新坐標(x1,y1);
(5)在屏幕上打出(x0,y0);
(6)重返第(2)步,進行下一次的迭代,直到迭代次數大于總步數為止.
在迭代算法中,Wk(k=1,2,3,…,N)是一組收縮仿射變換,式(2)稱為線性IFS迭代表達式.
3 基于MATLAB的自然景物中樹的模擬
由于分形幾何的特點,使其理論在自然景物的模擬方面具有很好的模擬效果。云、山、水、樹等自然景物通過計算機程序能夠較好的模擬,見圖2所示。
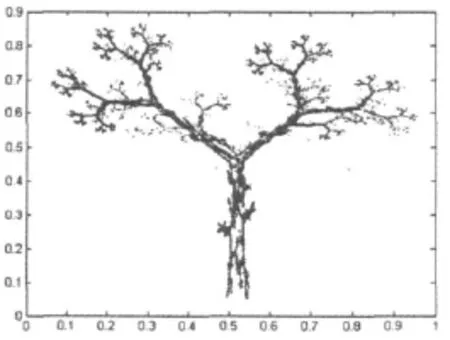
圖2 樹的模擬
通過對自然景物模擬問題算法的分析和求解,利用MATLAB矩陣工具中的模型語言算法去解決自然景物模擬過程中中的模擬和收斂問題[3]。MATLAB矩陣工具作為通用計算和模型求解的的良好平臺,有著強大的數學計算能力和豐富的編程接口,對自然景物模擬求解問題有著很好的解決手段,對分形理論的應用和改進有著重要的科學價值。因此,MATLAB工具已經在分形理論自然物仿真模擬領域中選擇為標準的問題求解軟件工具之一。
MATLAB是強大的矩陣工具,在自然景物模擬領域中的問題求解中有著廣泛的應用,其特點是對復雜的模型問題可以很好的分解、輸入、分析和求解,程序執行速度快。MATLAB矩陣生成器提供了模型庫,用戶只需要很好的建立問題模型的相關數值和約束條件,利用此工具的演算,就可以得到問題的最優解。開發者只需通過建立的約束或目標函數,鍵入相應的數值,就可以對問題進行求解。MATLAB矩陣工具作為通用計算和線性求解的的基礎平臺,工具有著強大的數學計算能力和豐富的編程接口,還提供了科學算法的開發語言-M語言。掌握MATLAB矩陣工具,使用其中的M語言是可以使較大規模問題的輸入過程和求解過程得到簡化[4]。
利用MATLAB進行模型算法的優化設計可以很好的對自然景物模擬問題進行求解。優化求解的過程,計算方法簡單,避免了人工輸入大量的變量和約束條件,降低了時間復雜度,從而大大提高計算的準確性和程序執行速度[5]。
模擬初始數據如表1所示。
由此可見,利用Matlab對自然景物進行編程和分形模擬,具有一些優勢。其條件設置簡單、容易實現,而且,在相同硬件設置條件下比其他的程序語言具有更好的收斂速度和更快的生成速度.
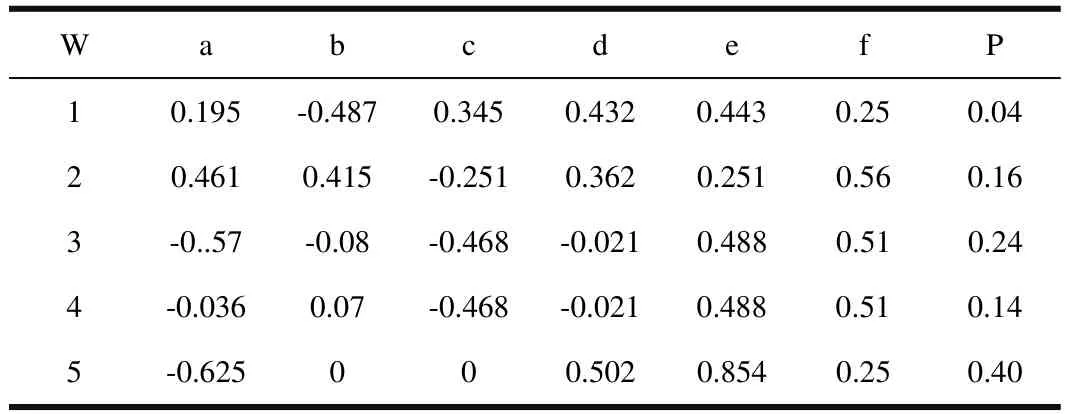
表1 模擬初始數據
4 結語
采用計算機技術對自然景物進行建模與仿真,可以在人類的生產生活中提供很多的便利,為物質財富的增加和精神世界的豐富提供了更多的實現手段。對自然景觀進行模擬,可以促進一部分傳統產業的發展,特別是在互聯網服務提供商、醫療、旅游、教育和學習領域,自然景物模擬都能發揮重要的作用。因此,在基于分形的自然景物模擬和仿真在研究領域具有深入挖掘的價值。
通過分形理論相關文獻的研究和對迭代函數系統(IFS)的基本原理的闡述解讀,采用IFS隨機迭代算法,利用Matlab軟件進行編程和仿真,較好的模擬了自然景物中樹的構造和圖像圖形,驗證了分形幾何理論,具有一定的實用價值。
[1]李彤,夏張莉,宿偉玲.求解丟番圖方程的模擬植物生長算法[J].中國管理科學.2012,(S1).
[2]唐衛東,李金忠,劉昌鑫,胡雪華,李萍萍,盧章平.虛擬植物模型及其構建方法研究綜述[J].計算機應用研究.2012,(09).
[3]劉穎,羅岱,黃心淵.基于OSG的Speedtree植物模型繪制研究[J].計算機工程與設計.2012,(06).
(責任編輯:文婷)
G42
A
1003-3319(2016)04-00013-02
10.19469/j.cnki.1003-3319.2016.04.0013

