二維彈性平板繞流鎖定發生機理研究

賈文超，陳美霞，楊 丹

(華中科技大學 船舶與海洋工程學院，湖北 武漢 430074)

二維彈性平板繞流鎖定發生機理研究

賈文超，陳美霞，楊 丹

(華中科技大學 船舶與海洋工程學院，湖北 武漢 430074)

本文采用雙向流固耦合來研究一端固定二維平板渦激振動特性，通過動網格技術來實現流場和結構之間力和位移的相互傳遞。對不同雷諾數下平板繞流渦分離進行計算，成功捕捉到了鎖定現象，并對其發生機理進行研究。計算結果表明，當渦脫落頻率接近結構固有頻率、結構表面壓力分布與結構模態一致、尾渦強度達到一定水平，即可產生鎖定現象。

鎖定；雙向流固耦合；渦激共振

0 引 言

艦船螺旋槳發出的“唱音”是螺旋槳噪聲中一種非常特別的噪聲源，它的產生與流固之間強耦合作用密切相關，這種強耦合作用即為“鎖定”現象。由于鎖定現象涉及到流場和結構 2 個方面，其發生機理非常復雜。Philippe Ausoni等[1]以三維等直翼型為研究對象，進行不同來流速度下水動力性能和振動特性試驗，試驗成功捕捉到鎖定現象，當渦脫落頻率接近結構扭轉固有頻率時，結構振級達到最大，且在鎖定雷諾數區間內，渦脫落頻率均與結構固有頻率保持一致。A.Zobeiri等[2]對不同隨邊形狀三維等直翼在不同來流速度下的渦激振動特性進行了試驗研究，試驗結果表明，尖銳隨邊比更鈍的隨邊更能降低鎖定雷諾數區間內的振級，但對鎖定頻率大小及區間寬度影響較小。Eliasson R等[3]給出了相同來流速度不同隨邊形狀翼型結構的振級，對稱隨邊更有利于上下緣漩渦交替發放，從而激發較強的渦激振動；非對稱隨邊則不利于漩渦的產生于發放，渦激振動振級較低。

彈性結構繞流鎖定研究的難點在于計算方法，需要采用雙向流固耦合方法進行計算。目前針對雙向流固耦合算法的研究，主要方法有 2 種：一種是采用彈簧振子系統來模擬，結構被視為剛體；另一種是流場和結構同步求解，每一時間步交換耦合面上的力和位移，考慮了結構彈性對流場的反饋效應。

B.S. Carmo等[4]對不同來流速度下彈簧-圓柱系統振動特性進行了數值模擬，將得到的頻率鎖定區間劃分為初始區域和穩定區域，在鎖定區間內結構響應并未

保持恒定，在初始區域內結構振級急劇上升達到峰值；而在穩定區域，振級逐漸下降。

隨著大型計算機的發展以及數值計算軟件的開發，雙向流固耦合計算成為了可能。Gluck等[5]采用CSD 和 CFD 數值算法軟件包來同時進行結構和流場 2個域的計算，通過 MPCCI 插值算法進行結構和流場兩個獨立耦合面節點之間位移和力的相互傳遞，從而將結構和流場 2 個域耦合在一起。Herwig Peters等[6]采用Workbench 中的多物理場耦合模塊對一端固支懸臂平板渦激振動進行了計算，研究了結構楊氏模量對懸臂板位移響應的影響規律。結果表明，當流體介質從空氣變為水后，結構共振楊氏模量增加；結構在動水中共振楊氏模量相比于靜水中楊氏模量并無顯著差異。

文獻[6]通過改變楊氏模量來研究鎖定現象，工程應用性不強。本文在其算法的基礎上，針對艦船螺旋槳經常出現的“唱音”現象，對一端固支柔性平板繞流進行了變來流速度的二維數值模擬，研究了其振動特性和水動力特性，對平板及翼型這類狹長結構繞流問題中常見的“鎖定”現象發生機理進行研究，為螺旋槳“唱音”問題的解決提供參考。

1 雙向流固耦合計算方法

1.1 初始流場控制方程

本文流場介質為不可壓黏性流體，且不考慮熱交換，在當前雷諾數下，選用基于時間平均的湍流模型。具體方法是將湍流運動看做是時間平均流動和湍流脈動 2 種運動的線性疊加，因此，可將速度和壓力進行如下處理：式中：u，v，w 為平均速度；u’，v’，w’ 為脈動速度；p 為平均壓力；p’ 為脈動壓力。

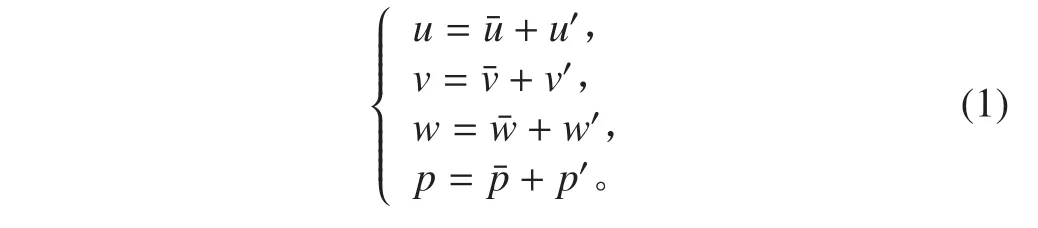
將其代入瞬態的 N-S 方程，可得時均化的動量方程[7]：

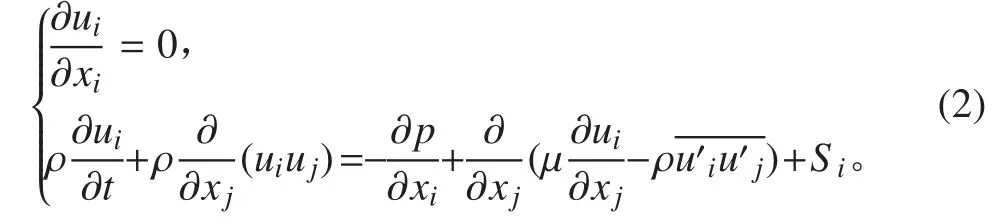
顯然上式多了一個應力項，需要引入湍流模型以使其封閉。本文采用 SST k-ω 湍流模型，本模型是一個結合了 k-ε 的分區域湍流模型，在靠近壁面的邊界層內使用 k-ω 模型，能更有效模擬較大的分離流動，而在遠離邊界層的自由流場中則使用 k-ε 模型，克服了 kω 對自由來流條件不太敏感的缺點，本模型是模擬平板繞流湍流運動的理想模型。

1.2 懸臂板振動控制方程

懸臂板受迫振動有限元控制方程為：

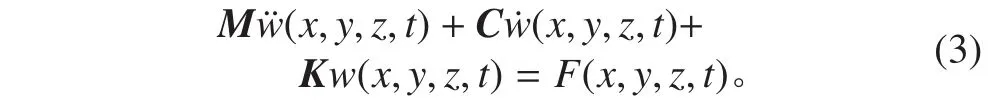
式中：M 為質量矩陣；C 為阻尼矩陣；K 為剛度矩陣；w 為節點位移；F 為平板表面分布激勵力，即第1.1 小節計算得到平板表面脈動壓力。

1.3 雙向流固耦合數據交換

雙向流固耦合的關鍵在于流場與平板之間的力和位移的相互傳遞，本文通過 Ansys Workbench 平臺中的System Coupling 模塊來實現這種傳遞。首先求解 1.1 小節中初始流場（平板視為剛體），得到剛性平板表面脈動壓力然后通過求解 1.2 小節中彈性平板控制方程，可得彈性平板表面位移響應。將作為流場內邊界的速度邊界條件，采用動網格技術，重新求解 N-S 方程，得到更新之后壁面壓力，再將其重新加載到結構表面，求解結構動響應，如此反復迭代，直至壓力和位移滿足收斂條件。圖 1 為懸臂平板雙向流固耦合求解流程圖。

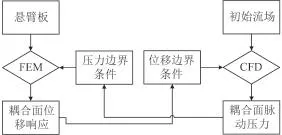
圖1 懸臂板雙向流固耦合求解流程圖Fig.1 Flow char of two-way fluid-structure interaction algorithm

2 數值計算模型

2.1 流場 CFD 模型及結構有限元模型

本文結構模型為二維彈性懸臂平板，其基本尺寸為：平板沿來流方向長 L = 0.41 m，平板厚度 t = 0.02 m，密度 ρ = 7 850 kg/m3，楊氏模量 E = 32 921 Pa，泊松比 v = 0.3。平板有限元模型采用 solid186 單元，如圖 2 所示，沿來流方向劃分 216 份，沿厚度方向劃分 16 份，沿展向劃分 1 份，以模擬展向無限長平板，結構單元總數為 3 586。

流體計算域如圖 3 和圖 4 所示，流動方向為 x 軸

正向，y 軸方向為垂直于來流方向，左端流場入口邊界到平板左端的距離為 75 倍板厚，出口邊界到平板右端距離為 140 倍板厚，計算域上下邊界到平板上下壁面的距離為 40 倍板厚。網格劃分采用分塊劃分方法，結構近壁處采用加密的結構化網格，以更準確地模擬近壁面復雜的流動情況，遠場則采用稀疏的非結構化網格，確保獲得較快的計算速度。

圖2 懸臂板有限元模型Fig.2 Finite element model of plate

圖3 全局流場網格Fig.3 Fluid domain

圖4 近壁面網格Fig.4 Boundary layer

2.2 邊界條件

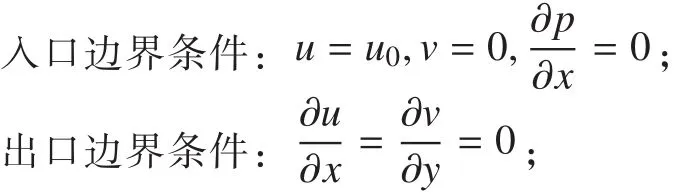
平板表面及流域上下為無滑移固壁：u = 0，v = 0。

2.3 數值求解方法

本文采用有限體積法來離散二維不可壓縮非定常粘性流體控制方程（2），動量采用二階迎風格式，時間項采用一階隱式積分法，速度和壓力耦合項采用Simple 算法來求解。

3 彈性平板振動特性分析

由于雙向流固耦合計算十分緩慢，為了捕捉到平板鎖定現象，在進行雙向流固耦合計算之前，需要確定計算雷諾數區間。靜水中懸臂平板第 2、3 階固有頻率分別為 0.184 5 Hz 和 0.567 5 Hz，通過對剛性平板繞流進行試算，雷諾數為 500 和 1 280 時，渦脫落頻率分別為 0.185 7 Hz 和 0.561 8 Hz，與平板第 2、3 階固有頻率比較接近，因此，在 500 和 1 280 這 2 個雷諾數附近進行變速度雙向流固耦合計算。

圖 5 給出了雙向流固耦合算法下不同雷諾數懸臂板最大位移響應計算結果。圖 5（a）為結構第 2、3 階共振峰，圖 5（b）為結構第二階共振峰局部放大圖。從圖 5（a）可以看出，當雷諾數在 500 和 1 280 附近，平板發生極大的位移響應，這 2 個峰值工況對應的彈性平板尾部渦發放頻率分別為 0.186 4 Hz 和 0.557 3 Hz，與表 2 中得到的靜水中平板第 2 階和第 3 階固有頻率基本吻合，在這 2 個雷諾數下，懸臂板被漩渦激發而產生共振。觀察圖 5（b），當雷諾數接近鎖定區間時，懸臂板自由端位移響應緩慢增大到“位移平臺”區，而當雷諾數超過鎖定區間上限 532 時，結構位移響應迅速下降。

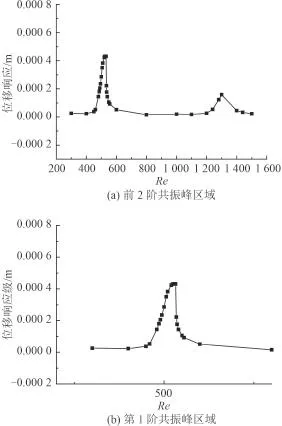
圖5 不同雷諾數下 2 種算法得到自由端總響應的對比Fig.5 Bending vibration amplitude of the free edge with different Reynolds number

圖 6（a）給出了剛性和彈性平板渦脫落頻率隨雷諾數的變化關系。圖 6（b）給出了第 2 階共振峰處的頻率鎖定區間。雙向耦合算法在第 2 階渦激共振區域捕捉到鎖定現象，鎖定雷諾數區間為 520～532。在該區間內，渦脫落頻率大體保持恒定，而剛性平板則不

能得到這樣的鎖定區間。

圖 7 為文獻[14]中給出的某翼型繞流表面一點速度響應隨雷諾數的變化曲線。本文得到的響應曲線與文獻[14]翼型實驗得到的曲線非常相似，規律基本一致。

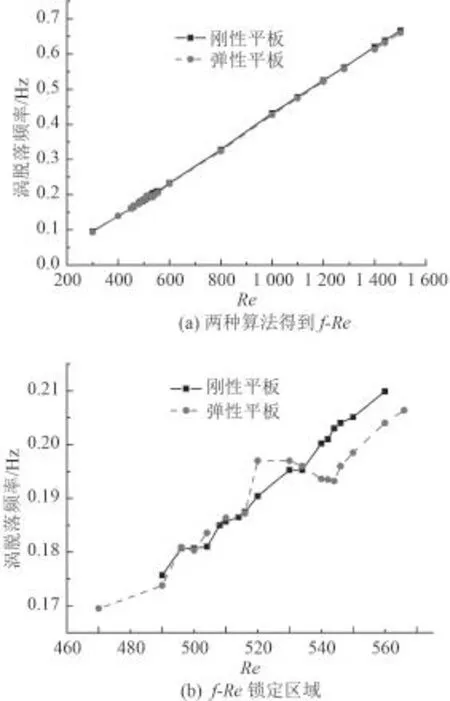
圖6 剛性及彈性平板的渦脫落頻率隨雷諾數的變化規律的對比Fig.6 Vortex shedding frequency of the rigid and elastic plate at different Reynolds number

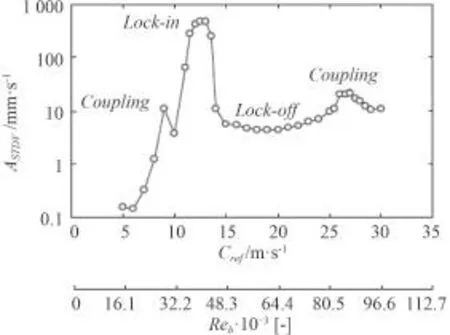
圖7 某固定翼型繞流位移響應[8]Fig.7 Vortex-induced vibration amplitude of a hydrofoil

4 鎖定形成條件研究

4.1 頻率條件

渦脫落頻率與結構固有頻率相一致為鎖定發生的前提條件。表 1 給出了平板固有頻率及圖 5（a）中 2個峰值工況下渦脫落頻率的對比。由表 1 可知，當渦脫落頻率接近結構某一階固有頻率時，漩渦將激發結構產生共振，此時流-固之間產生較強的耦合作用。

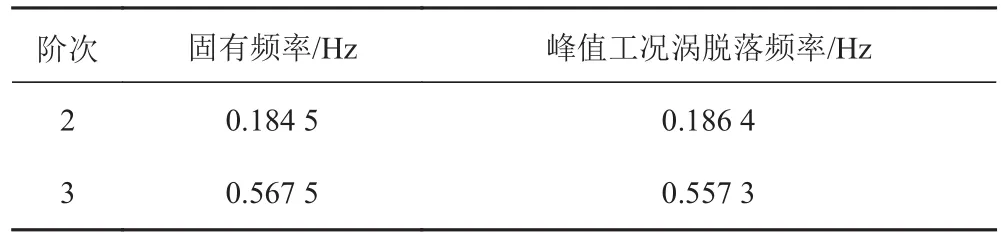
表1 平板固有頻率及對應峰值工況下渦脫落頻率的對比Tab.1 The second and third order natural frequency of the plate under water and votex shedding frequency of the elastic plate

圖8 靜水中平板第 2，3 階模態云圖Fig.8 The second and third order modes of the cantilever plate under water

4.2 脈動壓力分布條件

平板和翼型這類狹長結構更有利于渦激共振的產生，本質上是由于這種線型使得脈動壓力的分布特性與結構固有模態發生高度吻合，從而激發結構與流場之間的強耦合作用，最終產生鎖定。圖 9 所示為 2 個共振峰工況對應平板上下表面脈動壓力幅值分布，從導邊到隨邊，其幅值開始是緩慢增大，接近隨邊時則急劇增大，激勵力主要集中在平板自由端，而其他區域則非常小，這是因為渦激振蕩脈動壓力完全由尾渦脫落而產生，漩渦主要在尾部形成，因此激勵力也主要集中中尾端。圖 10 給出了平板法向脈動壓力合力沿流向的時域分布，由圖可知平板升力方向合力（激勵力）幅值自導邊至隨邊相位基本相同，而幅值則逐漸

增大，與圖 8（a）給出的結構第 2 階固有模態分布更加匹配。

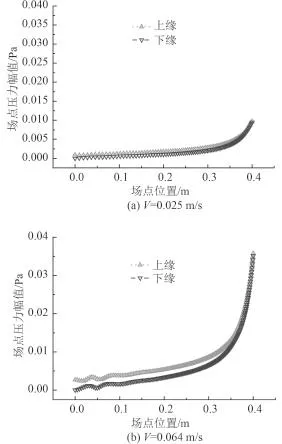
圖9 平板上下表面壓力幅值分布Fig.9 The pressure distribution along the upper surface and the lower surface

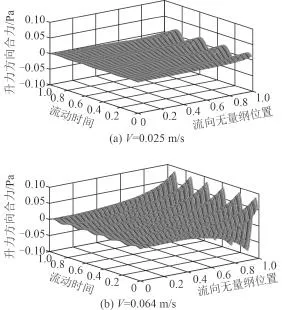
圖10 平板法向脈動壓力合力時域分布Fig.10 Normal pressure in time domain

從渦激振動幅值來看，圖 5（a）中第 2 階共振峰值明顯小于第 1 階的，而第 2 階共振峰工況對應平板表面脈動壓力明顯大于第 1 階，顯然這是由于脈動壓力分布特性與 1 階共振峰處的固有模態更加吻合。在第 2 階共振峰處，流-固之間耦合更加強，結構振級更高；而第 3 階共振峰處，激勵力分布與模態分布不再匹配，流固之間為弱耦合作用，結構振級較低。

4.3 隨邊形狀及尾渦強度條件

渦激振動強度與脈動壓力的幅值、相位與分布都密切相關，脈動壓力則是由結構尾部上下緣漩渦周期性交替發放產生，而不同的尾部形狀對漩渦的產生與脫落會產生重大影響。圖 11 所示為一剛性翼，弦長 1 m，攻角為 0，來流速度為 0.5 m/s，分別對隨邊厚度為0.02 m，0.03 m 和 0.04 m 三個剛性翼型進行繞流數值模擬。為了方便對比，各模型尾流場中渦量測點位置使用無量綱位置，3 種模型渦量監測測點分別取在距離隨邊 1 ～ 15 倍隨邊厚度處。

圖11 翼型形狀及尾流場測點分布Fig.11 Geometrical model and location of the measurement point in the wake

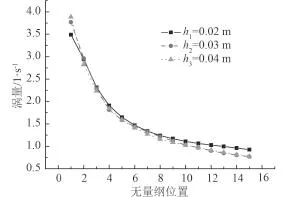
圖12 不同隨邊厚度模型對應渦強度的對比Fig.12 Vorticity magnitude of the foil with different thickness

圖 12 給出了不同隨邊厚度翼型尾流場中渦脫落與耗散過程中，漩渦中心強度的對比。由圖可知，相同來流速度下，較大的隨邊厚度翼型在近場將會形成強度較大的渦。鈍翼尾渦強度明顯強于尖翼，而隨邊處脈動壓力幅值也更大，更容易激起結構極強的振動，如圖 13 所示。圖 14 所示為不同隨邊厚度模型渦量

場，尾部越“尖銳”，越不易產生較強的漩渦發放；尾部越“鈍”，則越有利于漩渦的產生與發放。

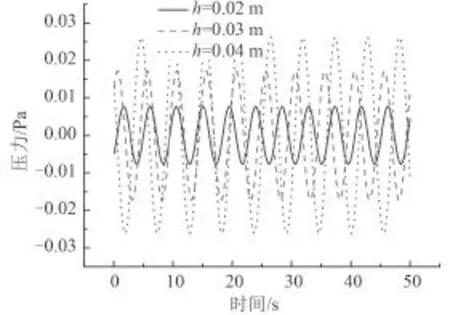
圖13 隨邊表面一點壓力時間歷程的對比Fig.13 The history of the pressure on the trailing edges with different thickness

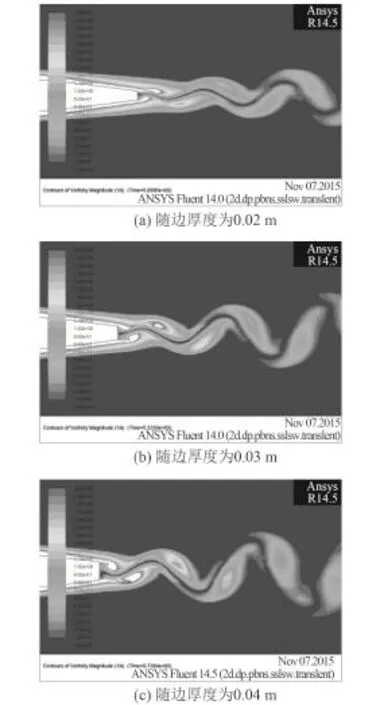
圖14 不同隨邊厚度模型對應渦脫落渦量云圖Fig.14 Vortex arrangement along the wake of the trailing edges with different thickness

5 結 語

本文采用計算流體力學方法和有限元方法來實現雙向流固耦合，并以懸臂平板為研究對象，計算在不同雷諾數下，彈性平板的振動響應特性，成功捕捉到了頻率鎖定現象，并給出了鎖定的形成條件，為螺旋槳唱音問題提供了指導方向，最終得到以下結論：

1）當懸臂平板尾部渦發放頻率與靜水中平板的固有頻率相一致的時候，尾部漩渦的周期性發放將會誘導平板產生極大的振動響應。

2）渦與結構發生“鎖定”現象，表現為結構位移響應峰值區域加寬，這是由于在共振頻率附近區域，結構表面脈動壓力幅值大小完全按結構模態分布，使得結構共振區域加寬。

3）結構和流場同時滿足頻率、壓力分布和隨邊形狀幾個條件時，流-固之間將產生強耦合作用，結構振幅達到最大，流場渦脫落頻率出現鎖定現象，在此鎖定區內，渦脫落頻率保持不變，結構振幅也保持在一個很高的水平。而在其他固有頻率處，雖能發生渦激共振，但振級大大低于鎖定時的振級，此時流-固之間的耦合相對較弱。

[1]AUSONI P, FARHAT M, AIT BOUZIAD Y, et al. Kármán vortex shedding in the wake of a 2D hydrofoil: Measurement and numerical simulation[C]//IAHR int. Meeting of WG on Cavitation and Dynamic Problems in Hydraulic Machinery and Systems. Barcelone, Spain, 2006 .

[2]ZOBEIRI A, AUSONI P, AVELLAN F, et al. How oblique trailing edge of a hydrofoil reduces the vortex-induced vibration[J]. Journal of Fluids and Structures, 2012, 32: 78–89.

[3]ELIASSON R, LARSSON L, ORYCH M. Principles of yacht design[M]. A&C Black, 2014.

[4]CARMO B S, SHERWIN S J, BEARMAN P W, et al. Flow-induced vibration of a circular cylinder subjected to wake interference at low Reynolds number[J]. Journal of Fluids and Structures, 2011, 27(4): 503–522.

[5]GLüCK M, BREUER M, DURST F, et al. Computation of fluid–structure interaction on lightweight structures[J]. Journal of Wind Engineering and Industrial Aerodynamics, 2001, 89(14/15): 1351–1368.

[6]PETERS H, CHEN L, KESSISSOGLOU N. The effect of flow on the natural frequencies of a flexible plate[C]//INTER-NOISE and NOISE-CON Congress and Conference Proceedings. Melbourne Australia: Institute of Noise Control Engineering, 2014: 610–616.

[7]ANDERSON J D, WENDT J F. Computational fluid dynamics[M]. New York: McGraw-Hill, 1995.

[8]AUSONI P. Turbulent vortex shedding from a blunt trailing edge hydrofoil[D]. Lausanne: école Polytechnique Fédérale de Lausanne, 2009.

Mechanism research of lock-in on two-dimensional flow around elastic plate

JIA Wen-chao, CHEN Mei-xia, YANG Dan
(School of Naval Architecture and Ocean Engineering, Huazhong University of Science and Technology, Wuhan 430074, China)

Vortex-induced vibration of a cantilever plate is investigated numerically based on two-way fluid-structure interaction, which is achieved through the exchange of force and displacement data between the fluid and the structure field. In this work, vortex-induced vibration of a cantilever plate at different Reynolds number is simulated, simultaneously successfully captures the lock-in phenomena, and the mechanism was studied. The results suggest that when the vortex shedding frequency is close to the natural frequency of the structure, the surface pressure distribution is consistent with the structure modal, vortex intensity reaches a certain level, the lock-in phenomenon will occur.

lock-in；two-way fluid-structure interaction；vorticity induced vibration

U661.1

A

1672 – 7619(2016)11 – 0028 – 06

10.3404/j.issn.1672 – 7619.2016.11.005

2016 – 03 – 01；

2016 – 07 – 29

國家自然科學基金資助項目（51179071）

賈文超(1986 – )，男，碩士研究生，主要研究方向為流激振動。