水下潛器姿態角的分數階 PID 控制研究

趙 健，白春江，章文俊

(大連海事大學 航海學院， 遼寧 大連 116026)

水下潛器姿態角的分數階 PID 控制研究

趙 健，白春江，章文俊

(大連海事大學 航海學院， 遼寧 大連 116026)

針對水下潛器縱向姿態角控制的穩定性問題，對水下潛器的姿態角控制系統設計一種分數階 PID 控制器。在控制器設計過程中，引入時間誤差絕對值（ITAE）準則，ITAE 準則的引入可快速獲得分數階 PID 的優化參數，設計優化分數階 PID 控制器。最后，以水下潛器的傳遞函數為仿真對象，分別采用分數階 PID 控制器和常規PID 控制器進行仿真研究。通過控制性能比較發現，本文所提出的分數階 PID 控制器的控制效果明顯優于常規 PID控制器，且分數階 PID 控制器具有更強的魯棒性。

水下潛器；分數階 PID 控制；魯棒性

0 引 言

船舶運動自動控制可大體概括為以下 5 類情況[1]：1）大洋航行自動導航；2）港區航行及自動靠離泊；3）擁擠水道航行或大洋航行自動避碰；4）船舶減搖控制；5）無人航海載運工具控制。其中的第 5 類控制問題，恰好體現了船舶運動控制發展的新趨勢[2]。自主式水下潛器（Autonomous Underwater Vehicle，AUV）的控制問題正屬于其中的第 5 類控制情況。

人的潛水深度有限，而且水下環境也較為惡劣，自主式水下潛器因為具有智能化、安全、活動范圍大、機動性好等方面的優點，目前已經發展成為了開發海洋與代替潛水員進行各種水下作業工作的重要工具。如在民用生產生活中，可用于深海石油勘測、航道排障、海底施工、港口作業、深海沉船考察、海上救助打撈及鉆井平臺水下結構檢修等；在軍事應用方面，可用于水下目標偵察、援潛、掃雷和救生等。在海洋開發工作中，自主式水下潛器起到的作用已經愈來愈重要，與此同時，對自主式水下潛器的性能要求也變得愈來愈高[3–4]。

由于受燃料消耗、水壓、速度變化等因素的影響，自主式水下潛器的數學模型參數具有較大的不確定性[5–6]，這給自主式水下潛器的控制系統設計帶來了較大困難，因此適宜采用魯棒控制方法來設計水下潛器的控制系統。近年來，許多不同的控制方法已經被應用到自主式水下潛器的各種運動控制研究中，如定量反饋

控制、H∞魯棒控制、模糊控制、滑模控制、線性二次型優化控制[5–9]等方法。文獻[5]為了解決水下潛器縱向姿態角控制問題，采用定量反饋理論設計了一種魯棒控制器，但設計過程中需要根據經驗預先設計出許多的性能指標并構造出適宜的頻率響應模板，具有較大的盲目性。文獻[6]利用定量反饋理論對 H∞魯棒控制器進行優化調整后，設計出了一種可用于水下潛器縱向姿態角控制的 H∞魯棒控制器，但控制器設計過程存在較大經驗依賴性和盲目性。文獻[7]將模糊控制與神經網絡相結合，提出了一種基于模糊控制的水下潛器沉浮控制方法，但其精準的模糊規則難以獲取，當規則過多，其計算負載將增加。文獻[8]針對水下潛器的姿態和位置控制問題，設計出了一種基于高階滑模算法的模型無關控制器，但是因為滑模控制方法自身的特性，使得系統仍然會出現一定的抖動現象。

PIλDμ控制器的概念是由 Podlubny 在 1997 年時提出的[10]。PIλDμ控制器除了兼具常規 PID 控制器的優點外，由于分數階微積分自身的特性，分數階控制器還具有許多整數階控制器無法實現的優越性，其微分階次 μ 和積分階次 λ 可以進行實數范圍內的任意設置，這使得 PIλDμ控制器具有比常規 PID 控制器更靈活的控制結構。近年來，一些研究者已經將 PIλDμ控制方法應用于航海領域，如船舶航向控制、船舶橫搖控制和船舶電站柴油機調速系統控制[11–13]，并取得了較好的控制效果。

本文針對水下潛器縱向姿態角控制的穩定性問題，進行分數階 PID 控制方法研究。在分數階 PID 控制器的設計過程中，引入 ITAE 準則對分數階 PID 控制器的參數進行優化，快速獲得分數階 PID 控制器的優化參數。同時本文對分數階 PID 控制器和常規 PID控制器的控制性能進行仿真實驗對比，探討 2 種控制器的穩態性能及魯棒性。

1 分數階微積分及分數階 PID 控制器

1.1 分數階微積分

分數階微積分是傳統整數階微積分的直接拓展，但它比整數階微積分具有更廣泛的適用性。所謂的分數階微積分是指階次為非整數的微積分，它可以實現任意階次的微積分。分數階微積分的算子可以由整數階微積分的算子直接擴展得到，其定義如下[14–15]：式中：a 為算子的下限；t 為算子的上限；α 為分數階微積分的階次，可以是任意復數，本文假定 α 為實數。

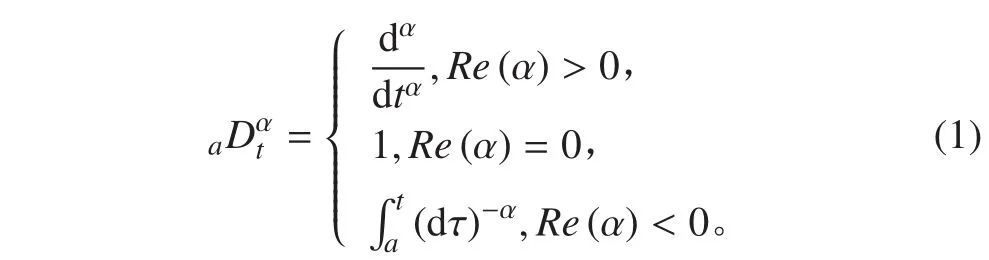
目前，在分數階微積分理論中較為常用的定義有以下 4 種[14,15]：

1）Cauchy 的表達式為：

我校近幾年分層走班教學活動搞得如火如荼。在這個過程中，我們特別重視以小組為主體，對學生進行人格培養，營造“創新教學”課堂教學形式，營造高效課堂。具體步驟是：以小組合作學習為平臺，教師和學生，學生和學生可以相互提問，相互補充，相互激勵，相互評價，達到培養思維品質，培養學生個性的目的。那么，作為語文教師，如何借助Blackboard平臺，通過小組合作學習，打造這種高效課堂呢？經過一年多的實踐，初顯成效，具體做法如下：

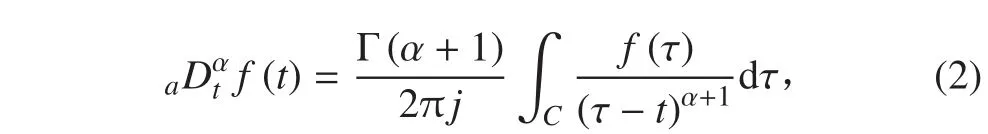
式中 C 為包圍 f（t）單值與解析開區域的光滑曲線。

2）Grunwald-Letnikov 的表達式為：

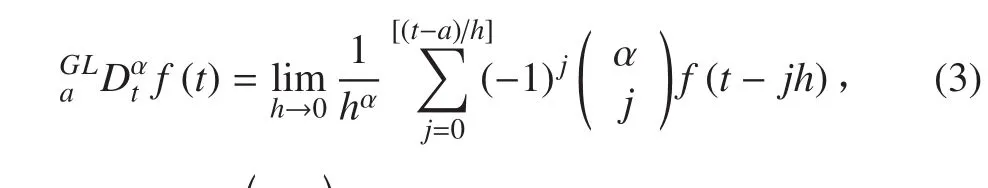
3）Riemann-Liouville 的表達式為：

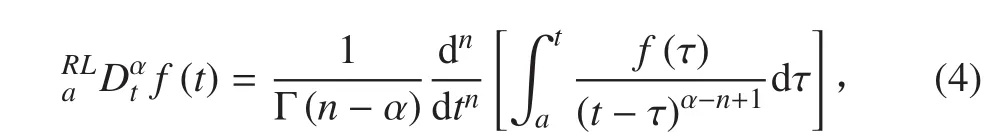
4）Caputo 的表達式為：

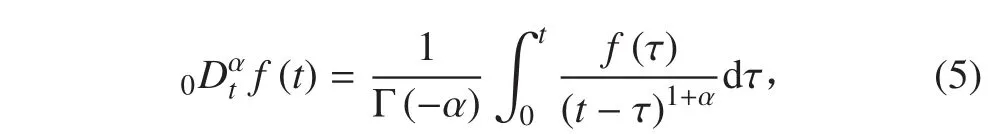
式中 α ＜ 0。

1.2 分數階 PID 控制器

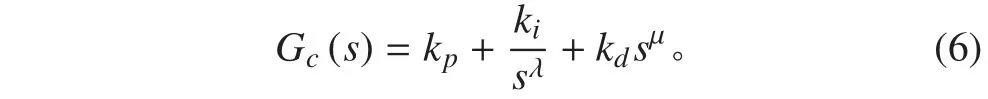
PIλDμ控制器的示意圖如圖 1 所示。其中，橫軸為PIλDμ控制器的積分階次 λ，縱軸為 PIλDμ控制器的積分階次 μ。常規的 PI 控制器、PD 控制器和 PID 控制器均為 PIλDμ控制器平面內的一個點。

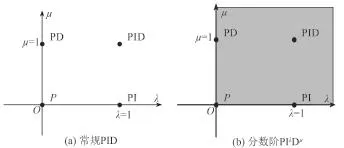
圖1 分數階 PIλDμ控制器示意圖Fig.1 Diagram of fractional-order PIλDμcontroller

通過比對可知，常規 PID 的 λ 與 μ 的值均為 1，是一種特例分數階 PID；與此類似，當 λ = 1，μ = 0 對應常規 PI 控制器；當 λ = 0，μ = 1 對應常規 PD 控制器。

此外，由于分數階 PID 的積分階次 λ 與微分階次 μ 可以是任意實數，這使得分數階 PID 控制器與整數階PID 控制器相比，具有更靈活的控制結構與優越的性能。

2 水下潛器的分數階 PID 控制器設計

2.1 水下潛器的傳遞函數模型

水下潛器的縱向姿態角控制通常選取彈道中極具代表性的 3 個典型工作點作為研究對象[16]，這 3 個典型工作點分別位于初始發射階段、中間階段與目標接近階段。假設舵角 δ 作為輸入信號，水下潛器的俯仰角 ψ 作為輸出信號，可以獲得不同階段水下潛器的傳遞函數模型 P1，P2和 P3。

2.2 水下潛器的分數階 PID 控制器

在設計水下潛器縱向姿態角控制的 PIλDμ控制器時，選取 P2為基準模型，其他 2 個模型用于驗證所設計控制器的魯棒性能[16]。在控制器設計過程中，為了能快速獲得 PIλDμ控制器的優化參數，提高控制器的控制性能，引入如下 ITAE 準則：

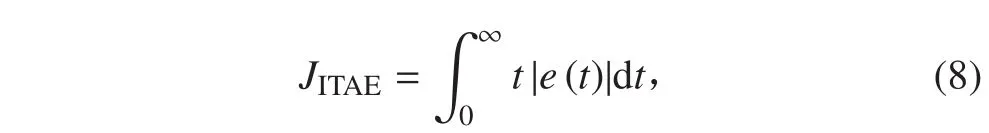
通過數值方法對 ITAE 準則指標進行優化，則可以得到優化后的 PIλDμ控制器參數，kp= 0.6，ki= 1.6，kd= 0.52，λ = 0.1，μ = 0.64。即優化 PIλDμ控制器為：

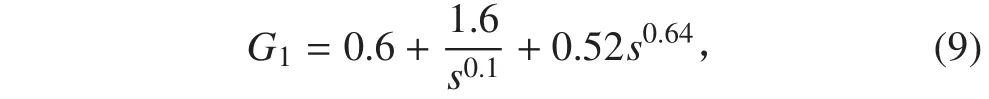
此外，采用常規 PID 控制器的設計方法[14]，可獲得常規 PID 控制器如下。

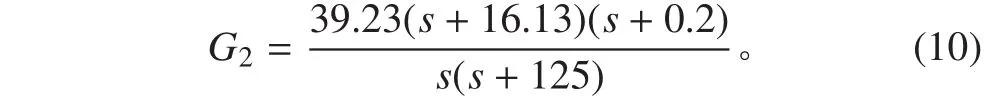
3 仿真實驗

針對基準模型 P2，進行水下潛器俯仰角閉環控制單位階躍變化時的瞬態響應仿真實驗，得到分數階PID 控制器和常規 PID 控制器的控制性能結果曲線，如圖 2 所示。

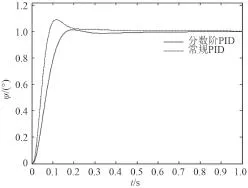
圖2 P2模型的仿真結果曲線Fig.2 Simulation result curve of model P2

其中，常規 PID 控制器的調節時間為 ts= 0.225 s，上升時間為 tr= 0.052 s，超調量 σ% = 9.2%。PIλDμ控制器的調節時間為 ts= 0.30 s，上升時間為 tr= 0.17 s，超調量 σ% = 1.5%。2 種控制器對模型 P1和模型 P3的控制仿真結果曲線分別如圖 3 和圖 4 所示。

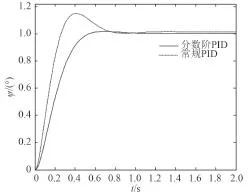
圖3 P1模型的仿真結果曲線Fig.3 Simulation result curve of model P1

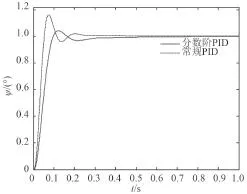
圖4 P3模型的仿真結果曲線Fig.4 Simulation result curve of model P3

對比以上的仿真結果可知，本文所設計的 PIλDμ控制器的控制效果明顯優于常規 PID 控制器，具有更好的穩態性能，且 PIλDμ控制器對 3 種模型均表現出了更為優越的魯棒性能，能很好地克服水下潛器由于外界因素干擾而導致的模型不確定性的影響。本文所設計的 PIλDμ控制器具有魯棒性強、穩定性好等優點。

4 結 語

針對水下潛器縱向姿態角控制存在的模型不確定性且系統對控制器魯棒性能要求較高的特點，引入 ITAE 準則后對控制器參數進行優化，設計出了一種分數階 PID 控制器。仿真結果表明，本文中設計出的分數階 PID 控制器可用于水下潛器的縱向姿態角控制，控制器的性能優于常規 PID 控制器，且控制器具有更為良好的魯棒性能。

[1]張顯庫. 船舶運動簡捷魯棒控制[M]. 北京: 科學出版社, 2012.

[2]ROBERTS G N. Trends in marine control systems[J]. Annual Reviews in Control, 2008, 32(2): 263–269.

[3]SHEN Y X, SHAO K Y, REN W J, et al. Diving control of autonomous underwater vehicle based on improved active disturbance rejection control approach[J]. Neurocomputing, 2016, 173: 1377–1385.

[4]KIM J, JOE H, YU S C, et al. Time-delay controller design for position control of autonomous underwater vehicle under disturbances[J]. IEEE Transactions on Industrial Electronics, 2016, 63(2): 1052–1061.

[5]肖永利, 張琛, 吳慶憲. QFT在水下潛器控制系統設計中的應用[J]. 上海交通大學學報, 1999, 33(4): 446–449. XIAO Yong-li, ZHANG Chen, WU Qing-xian. Application of QFT in Design of Underwater Vehicle Control System[J]. Journal of Shanghai Jiaotong University, 1999, 33(4): 446–449.

[6]肖永利, 張琛, 李振波, 等. 水下潛器的魯棒控制系統設計[J].上海交通大學學報, 1999, 33(11): 1348–1351. XIAO Yong-li, ZHANG Chen, LI Zhen-bo, et al. Design of robust control system for underwater vehicle[J]. Journal of Shanghai Jiaotong University, 1999, 33(11): 1348–1351.

[7]FOSSEN T I. Guidance and control of ocean vehicles[M]. New York: Wiley, 1994.

[8]豐少偉, 彭鵬菲, 姜俊. 基于模糊控制的水下潛器沉浮控制方法[J]. 電子設計工程, 2011, 19(5): 19–21, 25. FENG Shao-wei, PENG Peng-fei, JIANG Jun. Ups and downs control method of underwater submersible vehicle based on fuzzy control[J]. Electronic Design Engineering, 2011, 19(5): 19–21, 25.

[9]鄧春楠, 葛彤, 吳超. 基于高階滑模控制器的水下潛器運動控制[J]. 海洋工程, 2013, 31(6): 53–58, 96. DENG Chun-nan, GE Tong, WU Chao. Underwater vehicle motion control based on high order sliding controller[J]. The Ocean Engineering, 2013, 31(6): 53–58, 96.

[10]PODLUBNY I, DORCAK L, KOSTIAL I. On fractional derivatives, fractional-order dynamic systems and PIλDμcontrollers[C]//Proceedings of the 36th IEEE Conference on Decision and Control. San Diego, USA: IEEE, 1997.

[11]李光宇, 郭晨, 李延新. 基于改進粒子群算法的USV航向分數階控制[J]. 系統工程與電子技術, 2014, 36(6): 1146–1151. LI Guang-yu, GUO Chen, LI Yan-xin. Fractional-order control of USV course based on improved PSO algorithm[J]. Systems Engineering and Electronic, 2014, 36(6): 1146–1151.

[12]FAIEGHI M R, NADERI M, JALALI A A. Design of Fractional-Order PID for ship roll motion control using chaos embedded PSO algorithm[C]//Proceedings of the 2nd International Conference on Control, Instrumentation and Automation (ICCIA). Shiraz, Iran: IEEE, 2011: 606–610.

[13]李志民, 孫其振, 孫勇, 等. 基于BF-PSO的船舶電站柴油機分數階控制器[J]. 控制工程, 2012, 19(3): 515–518. LI Zhi-min, SUN Qi-zhen, SUN Yong, et al. Design of fractional-order controller for diesel engine system based on BFPSO[J]. Control Engineering of China, 2012, 19(3): 515–518.

[14]薛定宇, 陳陽泉. 高等應用數學問題的MATLAB求解(3版) [M]. 北京: 清華大學出版社, 2013.

[15]薛定宇. 控制系統計算機輔助設計-MATLAB語言與應用(3版)[M]. 北京: 清華大學出版社, 2012.

[16]ZHANG X K, JIN Y C. Transfigured loop shaping controller and its application to underwater vehicle[J]. International Journal of Automation and Computing, 2005, 2(1): 48–51.

Research on fractional-order PID control for underwater vehicle attitude angle

ZHAO Jian, BAI Chun-jiang, ZHANG Wen-jun
(Navigation College of Dalian Maritime University, Dalian 116026, China)

Aiming at the stability problem of the control of underwater vehicle longitudinal attitude angel, a Fractional-Order Proportional Integral Derivative (FOPID) controller is presented for underwater vehicle attitude angel control system. While designing the FOPID controller, the integrated product of time and absolute error standard (ITAE) is adopted to fast optimize the parameters of FOPID controller. Finally, the transfer function of underwater vehicle is chosen as the subject investigated, and simulation experiments of FOPID and classical PID controllers are carried out. By comparing the control performance of the two different controllers, the FOPID controller presented has more satisfactory performance and stronger robustness.

autonomous underwater vehicle；fractional-order proportional integral derivative control；robustness

U664.82+2

A

1672 – 7619(2016)11 – 0129 – 04

10.3404/j.issn.1672 – 7619.2016.11.027

2016 – 05 – 09；

2016 – 06 – 28

遼寧省自然科學基金資助項目(2015020622)；中央高校基本科研業務費資助項目(3132015002)

趙健(1980 – )，男，碩士，講師，研究方向為航海技術、海事安全及自動控制。