物理模型中膨脹巖相似材料濕度遷移規律研究

王軍輝，張新

（1.長沙理工大學，湖南長沙 410004；2.江西嘉圓房地產開發有限責任公司，江西南昌 330003）

物理模型中膨脹巖相似材料濕度遷移規律研究

王軍輝1，2，張新2

（1.長沙理工大學，湖南長沙 410004；2.江西嘉圓房地產開發有限責任公司，江西南昌 330003）

在研究不同初始含水率、不同密度膨脹巖巷道圍巖濕度場時，需在相似材料配比的基礎上進行物理模型試驗，模型填筑后的一段時間內填筑材料的含水率會受重力影響發生變化，模擬施工用水及其他水分時實測的圍巖含水率實際上是在重力影響下已發生變化的含水率，并不能精確反映施工用水對巷道圍巖的影響。文中通過對不同密度、不同含水率膨脹巖配比材料進行水分遷移試驗，得出了物理模型內部含水率隨時間的分布規律，為解決膨脹巖濕度場問題奠定基礎。

公路；膨脹巖；重力勢；含水率；密度；模型試驗

對于膨脹巖巷道圍巖濕度場的研究，圍巖內部水分的測定尤為重要，關系到圍巖膨脹力的大小，是圍巖膨脹應力計算的基礎。而膨脹巖這種似巖非巖、似土非土且對水敏感的軟巖吸水膨脹、失水收縮的特性，對含水率的精度要求更高。對膨脹巖巷道圍巖濕度場常采用物理模型試驗的方式進行研究，通過相似材料的配比試驗得到理想的配比，通過配比按照相似模型的比例填筑模型。模型筑好需穩定一段時間再進行巷道開挖及模擬，此時正是重力勢對模型內含水率的作用時段。為此，該文針對90 cm×90 cm×30 cm模型進行不同密度、不同初始含水率下膨脹巖配比材料試驗研究，探討重力作用下的水分遷移規律。

1 試驗設計

1.1 試驗材料及方案

在室內進行相似材料配比，其中：砂膠比為1∶1；石膏∶膨潤土及高嶺土=1∶1，膨潤土∶高嶺土=5∶2，淀粉1.5%。采用壁厚2 mm、內徑4.7 mm的長度為90 cm的PVC管進行材料填裝，兩端用塑料布密封后在底部留一小孔，保證水分能暢通。考慮3種初始含水率、3種密度的膨脹巖配比材料，共進行10組試驗（見表1）。

膨脹巖的基本指標：自由膨脹率為103.3%；干燥飽和吸水率為52.3%；極限膨脹量為31.2%；單軸抗壓強度為0.535 MPa。

1.2 試驗過程（見圖1）

試驗前按照PVC管的體積與密度計算材料用量，配制不同初始含水率的膨脹巖材料，材料配好后

充分浸潤12 h后進行填裝，填裝前測定2個初始含水率（取平均值）。取90 cm PVC管一段密封后按每層5 cm的高度用量進行填充，用自制夯實管進行分層擊實，通過質量和體積控制方法控制密度，填充完后直立靜置48、72、96、120 h。用割管鋸沿縱向鋸開，沿管縱向距管頂10、30、45、60、80 cm處取芯，用烘箱烘干測定含水率。

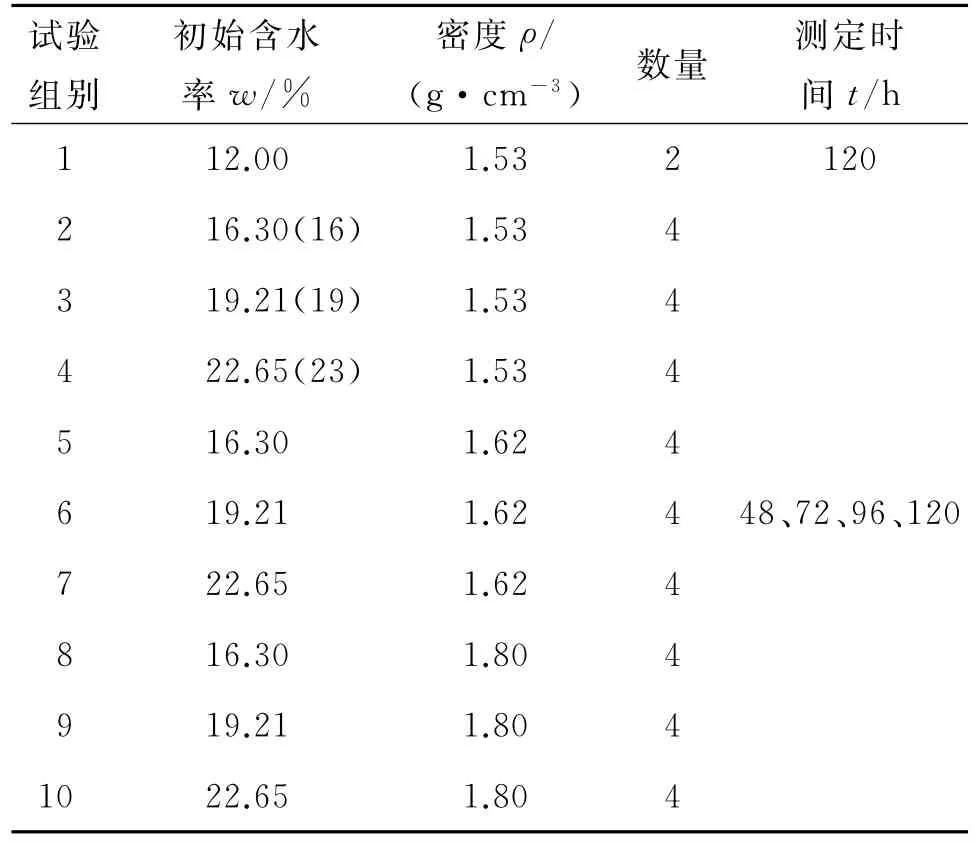
表1 試驗方案

圖1 試驗過程

圖2 含水率為22.65%的膨脹巖材料在靜置不同時間后的含水率分布

2 試驗結果分析與應用

2.1 試驗結果分析

通過試驗，得到不同初始含水率、不同密度下膨脹巖配比材料在豎向高度的水分變化規律。圖2為初始含水率為22.65%的膨脹巖材料在靜置不同時間后的含水率分布。從圖2可看出：初始含水率為22.65%的膨脹巖材料在靜置不同時間后不同高度處的含水率呈現微小變化，在中心靠下的上部水分減小，下部水分增大，但變化值很小。在48 h后，密度為1.53 g／cm3的材料其含水率最大減小值（距管頂部10 cm處）為0.74%，最大增大值（距管底部10 cm處）為0.5%；密度為1.8 g／cm3的材料最大減小值為0.18%，最大增大值為0.14%；密度值為1.62 g／cm3的材料介于上述兩種材料之間，最大減小值為0.5%，最大增大值為0.24%。在72 h后，呈現上部含水率繼續減小、下部含水率繼續增大的趨勢，密度為1.53 g／cm3的材料最大減小值為0.98%，最大增大值為0.55%；密度為1.8 g／cm3的材料最大減小值為0.23%，最大增大值為0.18%；密度為1.62 g／cm3的材料最大減小值為0.7%，最大增大值為0.28%。在96 h后，密度為1.53 g／cm3的材料最大減小值為1.23%，最大增大值為0.63%；密度為1.8 g／cm3的材料最大減小值為0.27%，最大增大值為0.25%；密度值為1.62 g／cm3的材料最大減小值為0.78%，最大增大值為0.33%。在120 h后，密度為1.53 g／cm3的材料最大減小值為1.44%，最大增大值為0.68%；密度為1.8 g／cm3的材料最大減小值為0.34%，最大增大值為0.33%；密度為1.62 g／cm3的材料最大減小值為0.84%，最大增大值為0.39%。可通過插值的方式得出該含水率下其他密度材料靜置48、72、96、120 h后的含水率變化曲線。

圖3 含水率為19.21%的膨脹巖材料在靜置不同時間后的含水率分布

圖3 為初始含水率為19.21%的膨脹巖材料在靜置不同時間后的含水率分布。從圖3可看出：初始含水率為19.21%的膨脹巖材料在靜置不同時間后不同高度處的含水率變化趨勢仍舊是中心左右位置以上的含水率減小、下部含水率增大，減小和增大幅度比初始含水率為22.65%的材料稍小。在48 h后，密度為1.53 g／cm3的材料其含水率最大減小值為0.54%，最大增大值為0.48%；密度為1.8 g／cm3的材料最大減小值為0.3%，最大增大值為0.29%；

密度為1.62 g／cm3的材料最大減小值為0.47%，最大增大值為0.31%。在72 h后，密度為1.53 g／cm3的材料最大減小值為0.63%，最大增大值為0.57%；密度為1.8 g／cm3的材料最大減小值為0.36%，最大增大值為0.32%；密度為1.62 g／cm3的材料最大減小值為0.55%，最大增大值為0.38%。在96 h后，密度為1.53 g／cm3的材料最大減小值為0.75%，最大增大值為0.6%；密度為1.8 g／cm3的材料最大減小值為0.45%，最大增大值為0.44%；密度為1.62 g／cm3的材料最大減小值為0.67%，最大增大值為0.47%。在120 h后，密度為1.53 g／cm3的材料最大減小值為0.88%，最大增大值為0.72%；密度為1.8 g／cm3的材料最大減小值為0.3%，最大增大值為0.29%；密度為1.62 g／cm3的材料最大減小值為0.53%，最大增大值為0.48%。可通過插值的方式得出該含水率下其他密度材料靜置48、72、96、120 h后的含水率變化曲線。

圖4為初始含水率為16.3%的膨脹巖材料在靜置不同時間后的含水率分布。從圖4可以看出：初始含水率為16.3%的膨脹巖材料在靜置不同時間后不同高度處的含水率變化趨勢仍舊是中心左右位置以上含水率減小、下部含水率增大。在48 h后，密度為1.53 g／cm3的材料其含水率最大減小值為0.34%，最大增大值為0.33%；密度為1.8 g／cm3的材料最大減小值為0.15%，最大增大值為0.18%；密度值為1.62 g／cm3的材料最大減小值為0.23%，最大增大值為0.27%。在72 h后，密度為1.53 g／cm3的材料最大減小值為0.48%，最大增大值為0.41%；密度為1.8 g／cm3的材料最大減小值為0.19%，最大增大值為0.20%；密度值為1.62 g／cm3的材料最大減小值為0.35%，最大增大值為0.33%。在96 h后，密度為1.53 g／cm3的材料最大減小值為0.55%，最大增大值為0.44%；密度為1.8 g／cm3的材料最大減小值為0.25%，最大增大值為0.24%；密度值為1.62 g／cm3的材料最大減小值為0.41%，最大增大值為0.37%。在120 h后，密度為1.53 g／cm3的材料最大減小值為0.61%，最大增大值為0.46%；密度為1.8 g／cm3的材料最大減小值為0.3%，最大增大值為0.29%；密度值為1.62 g／cm3的材料最大減小值為0.27%，最大增大值為0.30%。可通過插值的方式得出該含水率下其他密度材料靜置48、72、96、120 h后的含水率變化曲線。

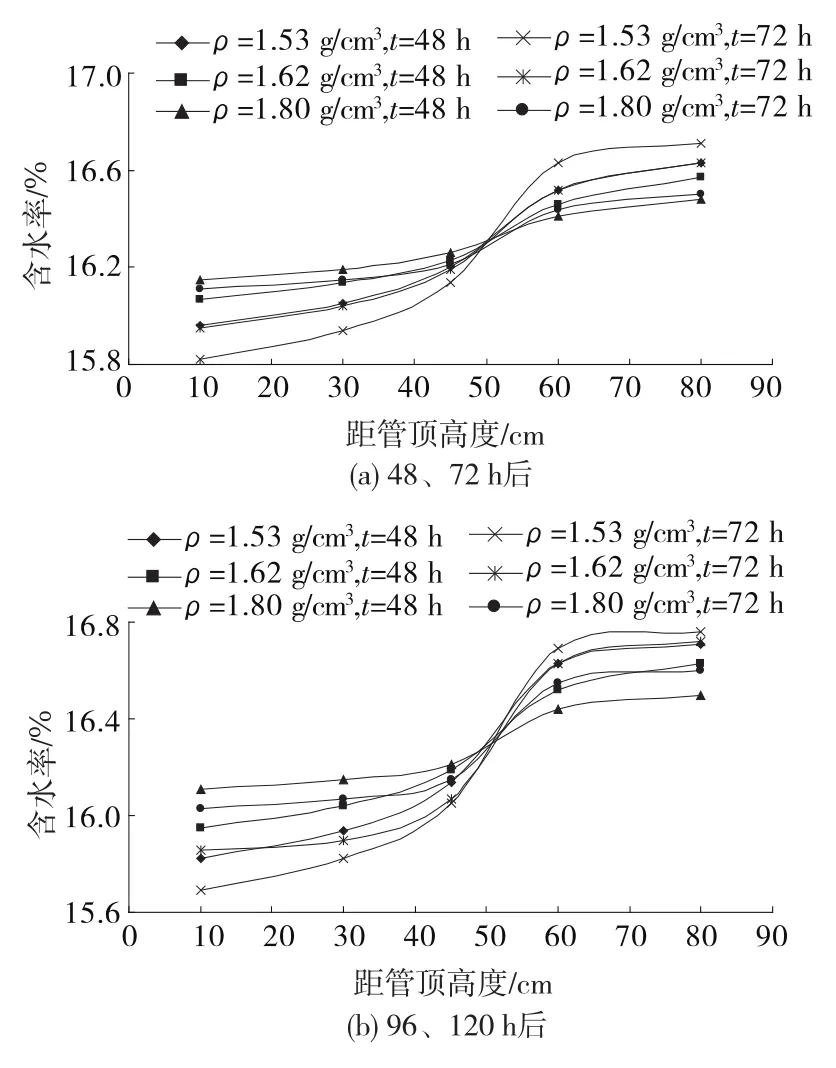
圖4 含水率為16.3%的膨脹巖材料在靜置不同時間后的含水率分布

圖5 為初始含水率為12%的膨脹巖材料在靜置120 h后的含水率分布。從圖5可以看出：初始含水率為12%的膨脹巖材料在靜置120 h后不同高度處的含水率基本為一條曲線，可以認為在12%含水率的重力勢作用下，沒有水分遷移的影響。故在后期模型上初始含水率可看作穩定值。

圖5 含水率為12%的膨脹巖材料在靜置120 h后的含水率分布

綜上所述，膨脹巖材料含水率的變化和其密度及初始含水率相關，但重力勢作用下的水分變化很小。從密度上考慮，密度1.8 g／cm3時水分變化最小，密度為1.53 g／cm3時水分變化稍大，密度為1.62 g／cm3時含水率變化介于兩者之間。從含水率上考慮，密度一定時，初始含水率高的變化值比含水率低的大。從試驗效果上看，初始含水率為22.65%的試樣下部有水分流失現象，初始含水率為12%的試樣含水率幾乎不變。

2.2 試驗結果應用

水分的遷移規律很復雜，由于試驗條件和時間的關系，僅從簡單的幾個點去分析模型中的水分變化其精度有限，但還是能通過試驗得出模型中任意初始含水率、密度在任意時間點和模型部位的含水率。在利用模型來研究水分變化規律時，可通過插值的方式得出相應曲線，從而確定任意點在具體時間上的含水率值，為后續試驗數據測量奠定基礎。例如要得出密度為1.7 g／cm3、模型初始含水率為17%、距離管頂40 cm處48 h的含水率，可通過上述1.8與1.62 g／cm3材料在48 h后的含水率變化曲線插值得出ρ=1.7 g／cm3材料含水率變化曲線，然后通過w=16.3%與w=19.21%各部位的值插值得出w=17%的各點值，從而得到其含水率變化曲線（見圖6），從圖6中可找出40 cm處的含水率值。若要得出60 h的含水率，只要再進行一次插值，即將48 h的數據與72 h的數據進行插值得出60 h的值。通過這種方法可更加精確地確定后期模型中進行水分濕度場研究的初始值。

圖6 密度為1.7 g／cm3膨脹巖材料靜置48 h后的含水率變化曲線

3 結論

（1）室內物理模型中膨脹巖相似材料在重力勢作用下水分會向下發生較小的遷移，初始含水率高的材料的水分遷移比初始含水率低的明顯，初始含水率在12%以下的材料其水分基本保持不變；初始含水率的影響程度比密度高，相同含水率下，低密度材料的水分遷移比高密度明顯。

（2）水分的遷移規律很復雜，通過一定的試驗，用插值的方法能計算出模型中任意初始含水率和密度材料在任意時間點和模型部位的含水率大小，使后期巷道圍巖在各工況下監測濕度場更加準確，在濕度場研究中具有一定的指導意義。

［1］ 繆協興，楊成永，陳至達.膨脹巖體中的濕度應力場理論［J］.巖土力學，1993，14（4）.

［2］ 盧義玉，侯吉峰，尤祎，等.濕度應力場作用下煤礦穿膨脹巖鉆孔縮徑規律研究［J］.采礦與安全工程學報，2014，31（3）.

［3］ 范秋雁.膨脹巖與工程［M］.北京：科學出版社，2008.

［4］ 付平勇.膨脹巖中巷道圍巖濕度場相似材料模型試驗研究［D］.南昌：華東交通大學，2013.

［5］ 董超.水分遷移對路基性狀影響的研究［D］.南昌：華東交通大學，2013.

［6］ 繆協興.用濕度應力場理論分析膨脹巖巷道圍巖變形［J］.中國礦業大學學報，1995，24（1）.

U416.1

A

1671-2668（2016）06-0087-04

2016-03-31