非線性濾波方法及其性能比較*

郭 彥 于艷婷 胡獻君

(1.海軍航空兵學院 葫蘆島 125000)(2.91329部隊 威海 264200) (3.海軍工程大學 武漢 430033)

?

非線性濾波方法及其性能比較*

郭 彥1于艷婷2胡獻君3

(1.海軍航空兵學院 葫蘆島 125000)(2.91329部隊 威海 264200) (3.海軍工程大學 武漢 430033)

針對非線性估計問題，對擴展卡爾曼濾波、無跡卡爾曼濾波以及容積卡爾曼濾波等常見非線性濾波方法的一般原理和步驟進行了描述，以微小型飛行器姿態估計問題為例，對非線性濾波方法的估計精度和運行效率進行了對比分析，為實際的非線性估計問題的處理提供了參考。

非線性濾波； 擴展卡爾曼濾波； 無跡卡爾曼濾波； 容積卡爾曼濾波； 性能比較

Class Number V448.22；TP301.6

1 引言

對于估計問題，實際當中的系統根本上都是非線性的，因此需要非線性濾波方法進行處理。

擴展卡爾曼濾波(Extend Kalman Filter, EKF)[1～2]以及無跡卡爾曼濾波(Unscented Kalman Filter, UKF)[3～4]是廣泛應用的非線性濾波方法。通過對非線性系統的一階線性化近似，EKF能夠較好地處理一般的非線性系統，但是由于忽略了系統的部分非線性特性，當系統的非線性特性較為突出、初始誤差較大時，EKF存在估計效果急劇下降和濾波收斂速度緩慢的問題，不能達到可靠的估計效果[5]。UKF采用無跡變換進行隨機變量傳播，以獲取更為準確的非線性函數概率分布，能夠更好地應對非線性特征突出的非線性系統估計問題[4]。但是UKF需要對三個可調參數進行適當選擇才能達到良好的濾波相關，且需要2n+1個采樣點，收斂時間相比于EKF有一定的增加[6]，在工程實現上存在限制[7]。而文獻[8～9]針對非線性系統估計問題提出的容積卡爾曼濾波(Cubature Kalman Filter，CKF)，使用一組等權值的容積點集來計算非線性變換后的隨機變量的均值和協方差，具有更優的非線性逼近性能(三階矩)、數值精度以及濾波穩定性，同時具有實現簡單、運算時間短的特點，目前廣泛應用于數據融合[10]、姿態估計[11]以及移動機器人位姿估計[12]問題中。

本文對常見非線性濾波方法的一般原理和濾波步驟進行了介紹，并結合微小型飛行器姿態問題對其性能進行了詳細對比，為實際的非線性估計問題的處理提供了參考。

2 非線性濾波方法

2.1 擴展卡爾曼濾波

假設一個非線性系統：

(1)

其中：xk∈Rn為k時刻系統的狀態向量，f為n維向量函數，zk∈Rm為k時刻系統的觀測向量，h為m維向量函數，wk為均值為零、協方差為Qk的n維隨機過程噪聲，vk為均值為零、協方差為Rk的m維隨機量測噪聲，且wk、vk互不相關。擴展卡爾曼濾波步驟描述如下。

1) 初始化

(2)

2) 時間-狀態更新

(1)計算狀態方程的雅各比矩陣:

(3)

(2)時間更新:

(4)

(3)計算量測方程的雅各比矩陣:

(5)

(4)量測更新:

(6)

(5)狀態更新

(7)

2.2 無跡卡爾曼濾波

無跡變換(UnsentedTransformation,UT)最早由Julier等提出，其基本原理是作者認為“對非線性系統狀態分布的近似遠比對非線性函數的近似簡單”[13]。該算法通過選取一組采樣點(Sigma點)來逼近系統的后驗均值和協方差，避免了對非線性系統的線性化處理，同時也避免了求解Jacobian矩陣或Hessian矩陣，且達到了至少二階以上的后驗均值和協方差值的估計精度，成為了近年來非線性濾波領域的研究熱點之一。用UT變換替換EKF中線性化的統計特性(均值、協方差)傳播，可得無跡卡爾曼濾波，具體步驟如下。

1) 初始化

(8)

2) 時間更新

(1)Sigma點選取和權值計算：

(9)

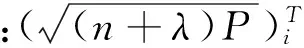
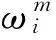
(10)

(11)

(12)

3) 量測更新

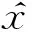
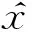
(13)

對應的均值以及協方差權值如式(10)和(11)。

(2)計算量測的一步預測、方差以及互協方差：

(14)

4) 狀態更新

狀態更新過程計算系統狀態增益矩陣、估計值以及狀態誤差方差：

(15)

2.3 容積卡爾曼濾波

CKF的核心思想是通過三階容積積分原理，計算函數的標準加權高斯積分[12]。標準的CKF步驟與UKF相似，區別在于采樣點的計算有所不同。

1) 時間更新

(1)設k-1時刻協方差矩陣Pk-1|k-1正定，對其進行因式分解得到Sk-1|k-1，即

(16)

(2)容積點估計

(17)

(3)容積點傳播

(18)

(4)求解狀態一步預測值

(19)

(5)計算預測誤差協方差矩陣

(20)

其中：Qk-1表示系統噪聲協方差矩陣。

2) 量測更新

(1)預測誤差協方差矩陣分解

(21)

(2)容積點估計

(22)

(3)容積點傳播

(23)

(4)計算量測預測值

(24)

(25)

(26)

其中：Rk表示量測噪聲協方差矩陣。

3) 狀態更新

(1)求解Kalman增益

(27)

(28)

3 仿真分析

3.1 問題描述

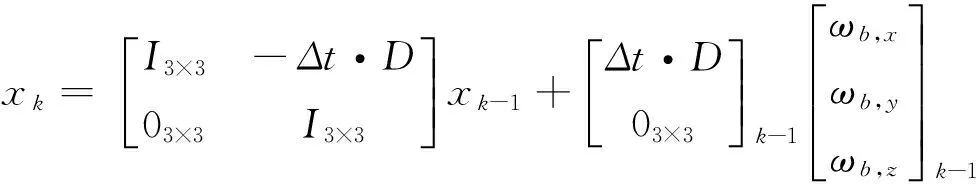
(29)

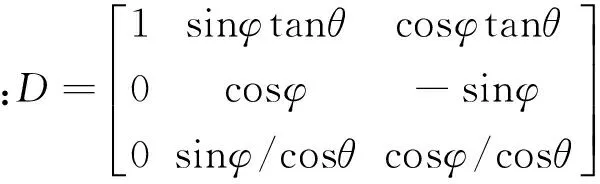
量測為根據加速度計與磁強計的輸出求解得到的姿態角，方程為

(30)

式中：wk為量測噪聲，其均值為零且方差為Rk。

3.2 仿真與分析

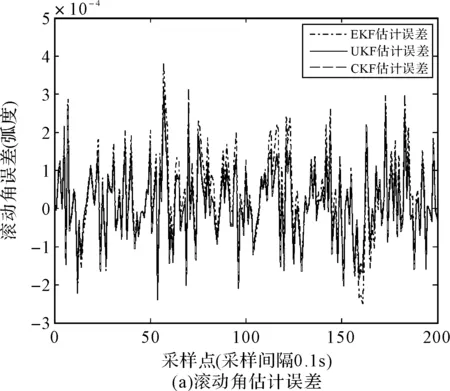
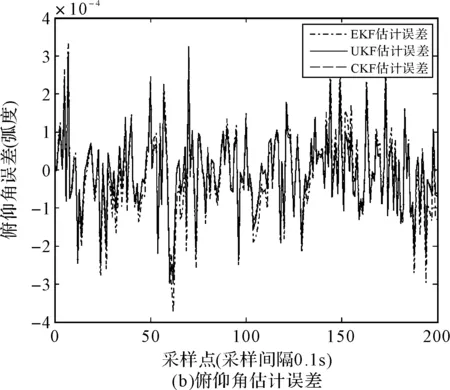
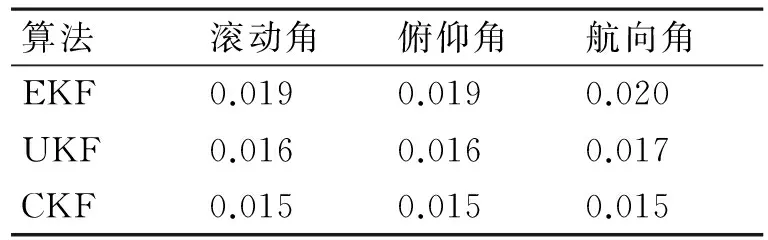
圖1 估計誤差比較

算法滾動角俯仰角航向角EKF0.0190.0190.020UKF0.0160.0160.017CKF0.0150.0150.015

1) 運算效率：EKF運算效率最高，CKF次之，UKF最差，具體為令EKF的100次Monte-Carlo仿真耗時為1，則UKF為1.89，CKF為1.67；

2) 估計精度：CKF最優，UKF次之，EKF最差，具體為相比于UKF、EKF，CKF在滾動、俯仰和航向三個維度上分別提高了(22.51%、9.94%)、(24.48%、9.94%)、(23.35%、10.12%)。

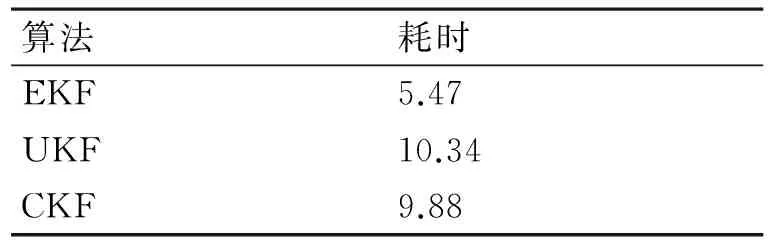
表2 EKF/UKF/CKF100次Monte-Carlo仿真耗時(s)

4 結語

本文對EKF、UKF以及CKF等常見的非線性濾波器的一般步驟進行了描述，并結合歐拉角描述的微小型飛行器姿態結算模型，對三個非線性濾波方法的估計精度、運算效率進行了對比，仿真結果表明，運算效率方面EKF運算效率最高，CKF次之，UKF最差，具體為令EKF的100次Monte-Carlo仿真耗時為1，則UKF為1.89，CKF為1.67； 估計精度方面，CKF最優，UKF次之，EKF最差，具體為相比于UKF、EKF，CKF在滾動、俯仰和航向三個維度上分別提高了(22.51%、9.94%)、(24.48%、9.94%)、(23.35%、10.12%)。

[1] A. Asadian, M. R. Kermani, and R. V. Patel. A novel force modeling scheme for needle insertion using multiple Kalman filters [J]. IEEE Trans. Instrum. Meas.,2012,61(2):429-438.

[2] M. Saha, R. Ghosh, and B. Goswami. Robustness and sensitivity metrics for tuning the extended Kalman filter [J]. IEEE Trans. Instrum. Meas.,2014,63(4):964-971.

[3] R. Kandepu, B. Foss, and L. Imsland. Applying the unscented Kalman filter for nonlinear state estimation [J]. J. Process Control,2008,18(7-8):753-768.

[4] D. H. Dini, D. P. Mandic, and S. J. Julier. A widely linear complex unscented Kalman filter [J]. IEEE Signal Process. Lett.,2011,18(11):623-626.

[5] 魏喜慶，宋申民.基于改進容積卡爾曼濾波的奇異避免姿態估計[J].航空學報，2013,34(3):610-619. WEI Xiqing, SONG Shenmin. Improved Cubature Kalman Filter Based Attitude Estimation Avoiding Singularity [J]. Acta Aeronautica et Astronautica Sinica,2013,34(3):610-619.

[6] 賈瑞才.重力/地磁輔助的歐拉角無跡卡爾曼濾波姿態估計[J].光學精密工程，2014,22(12):3280-3286. JIA Ruicai. Attitude estimation base on gravity/magnetic assisted Euler angle UKF [J]. Optics and Precision Engineering,2014,22(12):3280-3286.

[7] 劉華，吳文，王世元.基于平方根CKF的多傳感器序貫式融合跟蹤算法[J].系統工程與電子技術，2015,37(7):1494-1498. LIU Hua, WU Wen, WANG Shiyuan. Multrsensor sequential fusion tracking algorithm based on square-root cubature Kalman filter [J]. Systems Engineering and Electronics,2015,37(7):1494-1498.

[8] Arasaratnam I，Haykin S. Cubature Kalman filters [J]. IEEE Trans. on Autoynatic Control,2009,54(6):1254-1269.

[9] Arasaratnam I，Haykin S. Cubature Kalman smoothers [J]. Automatrca,2011,47(10):2245-2250.

[10] 胡振濤，曹志偉，李松，等.基于容積卡爾曼濾波的異質多傳感器融合算法[J].光電子激光，2014,25(4):697-703. HU Zhentao, CAO Zhiwei, LI Song, et al. Heterogeneous multrsensor fusion algorithm based on cubature Kalman filter [J]. Journal of Optoelectronics·Laser, 2014,25(4):697-703.

[11] 錢華明，黃蔚，葛磊.基于改進的迭代容積卡爾曼濾波姿態估計[J].哈爾濱工業大學學報，2014,46(6):116-122. QIAN Huaming, HUANG Wei, GE Lei. Attitude estimation based on improved iterated cubature Kalman filter [J]. Journal of Harbin Institiitf of Technology,2014,46(6):116-122.

[12] 康軼非，宋永端，宋宇，等.平方根容積卡爾曼濾波在移動機器人SLAM中的應用[J].機器人，2013,35(2):186-193. KANG Yifei, SONG Yongduan, SONG Yu, et al. Square-Root Cubature Kalman Filter and Its Application to SLAM of an Mobile Robot [J]. ROBOT,2013,35(2):186-193.

Nonlinear Filtering Methods and Performances Comparison

GUO Yan1YU Yanting2HU Xianjun3

(1. Naval Aviation Academy, Huludao 125000)(2. No. 91329 Troops of PLA, Weihai 264200) (3. Naval University of Engineering, Wuhan 430033)

Aiming at the problem of nonlinear estimation, the procedures of extended Kalman filter, unscented Kalman filter and cubature Kalman filter have been described, taking the attitude estimation problem of the micro aerial vehicle as an example, the estimation accuracy and the running efficiency of the nonlinear filtering methods are compared and analyzed, which provides a reference for the actual processing of the nonlinear estimation problem.

nonlinear filter, extended Kalman filter, unscented Kalman filter, cubature Kalman filter, performance comparison

2016年5月9日,

2016年6月17日

郭彥,女,碩士研究生,助教,研究方向:航空電子、高等教育理論。于艷婷,女,助理工程師，研究方向:指揮自動化。胡獻君,男,博士,助理研究員，研究方向:武器系統優化。

V448.22；TP301.6

10.3969/j.issn.1672-9722.2016.11.003