干發酵庫充氣密封圈非線性有限元分析

李瑞容， 朱德文， 王鵬軍， 韓柏和， 陳明江， 陳永生

(1.農業部南京農業機械化研究所， 南京 210014； 2. 農業部農村可再生能源開發利用重點實驗室， 成都 610041)

?

干發酵庫充氣密封圈非線性有限元分析

李瑞容1，2， 朱德文1， 王鵬軍1， 韓柏和1， 陳明江1， 陳永生1

(1.農業部南京農業機械化研究所， 南京 210014； 2. 農業部農村可再生能源開發利用重點實驗室， 成都 610041)

文章基于非線性有限元理論，考慮密封結構的材料特性、幾何形狀和接觸的非線性，建立了“M”形充氣密封圈的平面應變有限元模型，分析了充氣密封機理，得到了法向接觸應力沿密封接觸面的分布規律，討論了充氣壓力、被密封介質壓力和密封間隙對法向接觸應力和密封效果的影響。結果表明，保證密封效果的法向接觸應力隨充氣壓力的增大而增大，接觸橫截面寬度也隨之增長，在外表面中間的凹陷圓弧部分達到應力峰值；被密封介質壓力使得靠近介質一側的接觸應力減小，密封面長度變短；隨著密封間隙的增加，其接觸應力也相應增大。為了提升充氣圈的密封性能，需要結合密封圈的受力變形、環境溫度、壓力和材料特性等綜合進行結構設計，密封圈的表面應做涂層防腐處理；選擇適當的被密封介質壓力和充氣壓力比值，既能保證密封效果又能延長充氣圈的使用壽命。

充氣式密封； 非線性有限元； “M”形充氣圈； 硅橡膠

干法發酵具有產生沼液少、容積產氣率高、物料適應范圍廣和運行穩定的優點，無濕法發酵中的浮渣、沼液難處理等問題，受到了越來越多的關注。規模化沼氣干法發酵裝置主要有車庫型、氣袋型、滲出液存儲桶型、干濕聯合型和覆膜槽型等，其中車庫型干法發酵裝置容易實現擴展和規模化應用，具有運行管理簡單、能耗低、利用效率高、通用性強等優點，應用前景廣闊[1-3]。

為了滿足裝載機的快速進出料，發酵庫門一般開在發酵庫的側面，大門的密封面積大；密封面易有雜物，產生間隙；發酵物料成分復雜，腐蝕性強等問題導致密封難的現象。國內外已有學者開展了相關密封系統的研究，韓捷[4]等采用氣漲式夾緊密封方式對敞口式覆膜槽生物反應裝置進行密封，進出料方便，氣體易排盡，但密封面積大，密封效果難保障，且設計的深度和容量受密封面積大小所限；趙國明[5]等在地面車庫型發酵槽敞口處采用輔助加強膜式封口、雙閉合液漲式密封結構，反映直觀，安全可靠，但該方法僅適用于全年零度以上的地區，且密封面積過大，存在安全隱患；黑龍江省賓縣引進德國的密封技術，采用液壓驅動和粘黏式矩形充氣圈組合的密封方式，便于進出料，自動化程度高，但成本高，充氣圈底部易脫落，密封缺少可靠性和穩定性；陳永生、朱德文等研究開發的柔性頂膜車庫式干發酵裝置采用復合“M”形氣漲式機械壓緊密封技術，雙重密封安全可靠，可調節密封間隙，但需要空壓機供氣保證圈內氣壓。可見，針對復雜的沼氣運行工況，復合“M”形氣漲式機械壓緊密封技術是比較合適的密封方式之一。

目前，非線性有限元法被廣泛的應用于橡膠類密封圈數值模擬研究，但僅有少數針對充氣式密封結構，孟祥鎧[6]等利用MARC對“a”形充氣密封結構進行了分析，賁可存[7]等利用ANSYS對“V”形充氣式柔性密封圈進行了分析，周仕明[8]等利用MARC對充氣式自密封氣囊進行了分析，但對于“M”形充氣密封結構未見報道。本文利用大型有限元分析軟件ABAQUS，建立了截面結構為“M”形充氣密封圈的軸對稱有限元模型。分析了充氣圈的變形情況，以及充氣壓力、被密封介質壓力、密封間隙對法向接觸應力的影響，為充氣密封圈的結構設計和優化提供理論基礎。

1.密封圈墊片； 2.充氣密封圈I； 3.緊固圈部件； 4.螺栓； 5.平墊圈； 6.螺母； 7.充氣密封圈II； 8.密封圈卡箍； 9.大門門體圖1 復合“M”形充氣密封圈固定安裝方式示意圖

1 “M”形充氣密封圈結構和工作原理

發酵庫大門采用復合“M”形充氣圈組合密封技術，采用夾具固定的方式安裝在大門的四周，主要由兩個“M”形充氣密封圈、墊片、緊固圈、卡箍等組成，如圖1所示，兩道密封圈中間用緊固圈壓緊螺栓固定，兩側分別用墊片和卡箍加夾緊，使得密封圈既可以固定住也可以有一定的伸縮余量。

該充氣密封圈材料選用以硅橡膠為基體材料，白炭黑為增強纖維，并添加硅油和硫化劑等。形狀設計為“M”形，實際尺寸25 mm(寬度)×20 mm(高度)，壁厚3 mm。大門關閉后，利用空壓機對充氣圈加壓，充氣密封圈凹陷部位向外膨脹變形，與剛體門框相擠壓達到密封效果；當發酵完畢后，將充氣圈內的壓力卸載，密封圈脫離門框恢復充氣前“M”形。考慮到充氣密封圈因為長期工作磨損、氣壓不穩定等因素撕裂或泄漏，設計了兩道并行充氣密封圈，一旦其中一個密封圈發生破裂，另一個密封圈將保證發酵庫氣密性和穩定性。影響充氣圈密封性能的因素主要有充氣密封圈的接觸應力、結構形式、材料回彈性能、充氣壓力、被密封介質壓力、密封間隙大小以及接觸表面粗糙度[9]等。

2 “M”形充氣密封圈有限元模型

2.1 基本假設

(1)由于大門的門體、門框和固定件的剛度較大，不考慮其變形，將門框、固定件和接觸的門體視為剛體邊界；

(2)充氣密封圈采用的是硅橡膠材料，視為不可壓縮的而且在變形前是各向同性的;

(3)充氣密封圈沿著門框安裝在大門四周，周長遠大于密封圈的高度和寬度，因此，密封圈及其接觸邊界均按平面應變問題處理。

2.2 材料定義

確定彈性體材料的非線性特性是困難的，但基于應變能密度用于大彈性變形的幾種本構理論已經發展起來，對于橡膠類物理非線性材料，常用Mooney-Rivlin模型來描述[10]：

W=C10(I1-3)+C01(I2-3)

式中，C10和C01為Rivlin系數，均為正定常數。對于大多數橡膠而言，在應變為150%以內時可得到合理的近似。

采用兩參數的Mooney-Rivlin模型進行計算，待定的材料參數可通過理論估算的方法求得。該方法是建立在以下理論基礎上：初始剪切模量G= 2(C10+C01)和彈性模量E≈ 3G。利用橡膠材料的邵氏硬度HA計算彈性模量[8，11]。

再利用經驗公式(C10+C01)=E0/6，C01=0.25C10，即可得到兩參數的Mooney-Rivlin模型的材料參數值。

2.3 有限元模型

充氣密封圈材料為硅橡膠，硬度HA為55，采用Mooney-Rivlin模型，參數由上訴公式計算得出。根據氣囊的實際結構，考慮材料的不可壓縮性，對硅橡膠采用四節點四邊形完全積分不可壓縮Herrmann軸對稱單元，對大變形大應變的部位重劃網格保證單元的質量和計算的精度。模型中考慮密封圈底部與發酵庫門、密封圈頂部與門框的接觸，接觸間的摩擦采用庫侖摩擦模型，摩擦因數f=0.1，將充氣密封圈定義為變形體，采用離散描述；大門門體、固定件和門框定義為剛體，采用解析描述，并建立接觸體間的接觸關系。

根據實際工程運行情況，對該模型先施加內壓，待充氣密封圈膨脹穩定后，再施加被密封介質壓力。由于被密封介質壓力對充氣密封圈外表面作用范圍不可預知，采用預先加載充氣圈內壓力，待膨脹穩定后將實際接觸面的路徑用ABAQUS標記，再重新加載充氣圈內壓力和被密封介質壓力。該模型采用大位移全Lagrange格式的增量方法處理充氣密封圈的大變形幾何非線性問題，通過調整加載時間步長即可得到穩定的計算結果。

3 “M”形充氣圈密封性能分析

3.1 等效應力與變形分析

圖2～圖4顯示了充氣密封圈原始狀態的網格劃分情況，不同加載階段的整體變形和von-Mises應力分布情況。從圖2中可以看出，充氣密封圈未充氣時，呈現原始的“M”形，與頂部的大門門框存在一個密封間隙；如圖3所示，當充氣密封圈內充入一定壓力的氣體后，頂部的“M”形向外膨脹變形逐漸與頂部的大門門框貼合擠壓，將間隙填滿；如圖4所示，在充氣密封圈右側加載了被密封介質壓力Po后，密封圈右側部分受到擠壓脫離了與門框的接觸，接觸橫截面寬度變小。充氣壓力加載后，接觸面處充氣密封圈的應力分布呈軸對稱分布，其中凹陷圓弧部位的應力達到峰值，充氣密封圈的最大等效應力主要出現在“M”形左右兩側內部圓弧面、頂部凹陷圓弧與門框接觸面處。這主要由于這幾處圓弧部位發生了較大的彎曲變形，彎曲應力較大。因此，進行“M”形幾處圓弧角度的設計中，需選擇合適的倒角半徑，既保證有足夠的接觸應力，又不至于圈內應力長期過大使得工作壽命降低。

圖2 充氣密封圈原始狀態

圖3 充氣密封圈充氣狀態

圖4 充氣密封圈密封狀態

3.2 充氣壓力對接觸應力的影響

當密封間隙D=5 mm，被密封介質壓力Po=0 MPa時，對“M”形充氣密封圈分別充入0.10 MPa，0.15 MPa和0.20 MPa的壓力，如圖5所示為不同充氣壓力下沿著密封面的接觸應力分布曲線，可見法向接觸應力隨充氣壓力Pi的增大而增大。充氣密封圈膨脹后密封接觸橫截面寬度約為14 mm，接觸應力呈軸對稱分布，整體呈現中間突出的倒“U”曲線形式。在接觸面中間2 mm的長度范圍內，接觸應力隨著密封圈的過度膨脹急劇增大達到峰值，這主要由于密封圈“M”形中間的凹陷圓弧部分，受到充氣壓力的強力反方向擠壓，大幅度變形而造成。

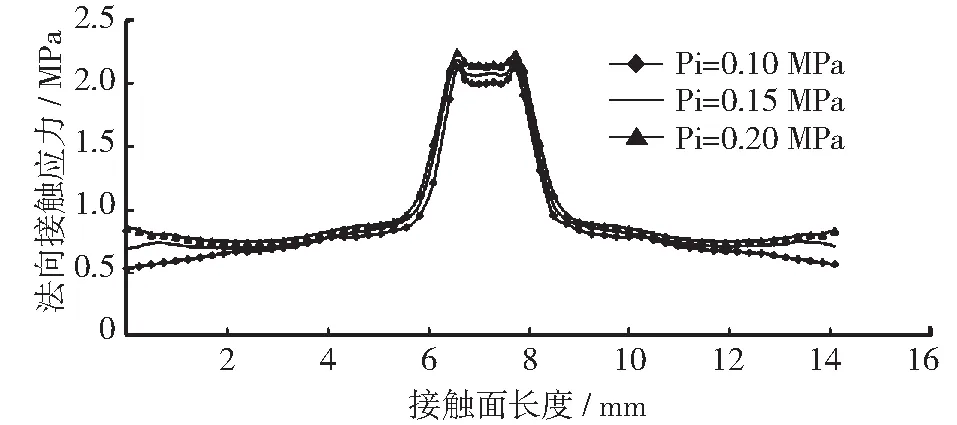
圖5 不同充氣壓力下接觸應力沿密封面分布曲線圖

為了確保充氣圈的密封效果，在密封連接結構的接觸面上，法向接觸應力必須大于或等于被密封介質的壓力。如圖5所示充氣圈內壓力在0.10 MPa～0.20 MPa之間，接觸應力值基本在0.50 MPa以上，最高達到2.24 MPa；正常工作時，被密封介質的壓力在0～1000 Pa之間，接觸應力遠遠大于被密封介質的壓力，且接觸應力峰值提高了充氣圈的密封性能。隨著充氣壓力的增大，法向接觸應力不斷增大，接觸橫截面寬度也隨之增長，充氣圈的密封性能不斷增強。但同時也需考慮到充氣圈的應力過大容易導致硅橡膠老化和密封失效，因此，要綜合分析選擇合適的充氣壓力。

3.3 被密封介質壓力對接觸應力的影響

圖6 所示為充氣壓力Pi=0.20 MPa，密封間隙D=5 mm時，不同被密封介質壓力下接觸應力沿密封面分布曲線圖。在“M”形充氣密封圈內加載0.20 MPa的壓力后，模擬工作狀態，在充氣圈的右側分別加載0 MPa，0.05 MPa，0.10 MPa的被密封介質壓力。從圖6中可知，密封圈與被密封介質接觸的一側在被密封介質壓力的作用下，法向接觸應力不斷減少，且波動較大；另一側的接觸應力略有增加；密封圈受到擠壓脫離了與門框的接觸，接觸橫截面寬度也隨之變短。

當密封圈受到庫內氣體和沼液的壓力作用時，密封面被迫發生分離，此時就要求密封圈能釋放出足夠的彈性應變能，能夠彌補這個分離量，并留有保持密封所需要的接觸應力[12]。因此，在提高密封圈的接觸應力的基礎之上，需選擇適當的密封介質壓力和充氣壓力比值，既能保證密封效果又能延長充氣圈的使用壽命。同時，為了提升充氣圈的吹出抗力，可以結合密封圈的受力變形、環境溫度和材料特性等綜合進行結構設計，例如加大充氣圈和門框密封面的摩擦力，特別是接觸密封介質的一側，密封圈的表面還應做一些涂層防腐處理。

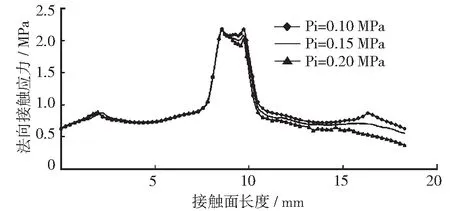
圖6 不同被密封介質壓力下接觸應力沿密封面分布曲線圖

3.4 密封間隙對接觸應力的影響

圖7所示為充氣壓力Pi=0.20 MPa,被密封介質壓力Po=0 MPa時，不同密封間隙下接觸應力沿密封面分布曲線圖。隨著密封間隙的增加，要求密封圈膨脹拉伸量也增加，導致其內部接觸應力也相應增大。

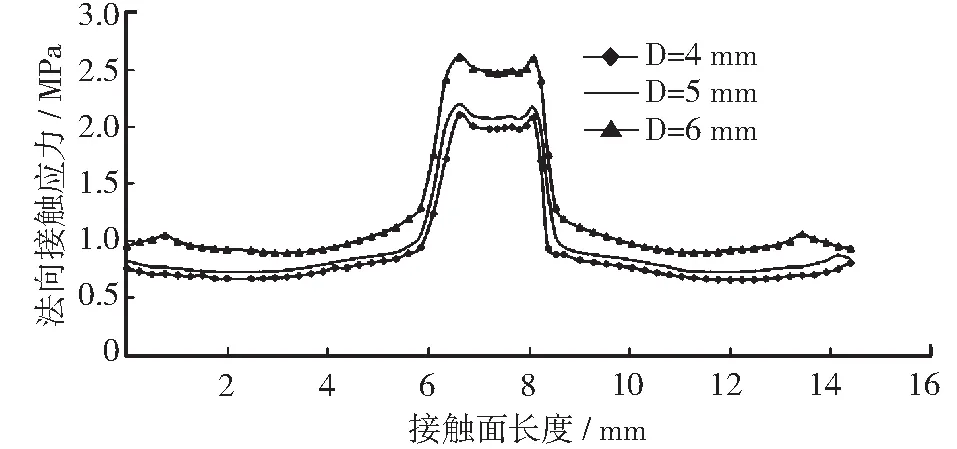
圖7 不同密封間隙下接觸應力沿密封面分布曲線圖

雖然密封間隙較大的時候，圈內的接觸應力也較大，能帶來較好的密封效果；但是，如果密封間隙過大，一方面會帶來接觸應力增加，大大降低了材料的使用壽命，對材料的性能要求較高；另一方面容易造成“M”形的展開程度不夠，即中間圓弧角半徑大的部位展不開，與密封面產生空洞，形成兩段接觸面，如圖8所示，為密封效果帶來隱患。因此，需要根據充氣圈的結構、材料、尺寸和充氣壓力、密封介質壓力，選擇合適的密封間隙。

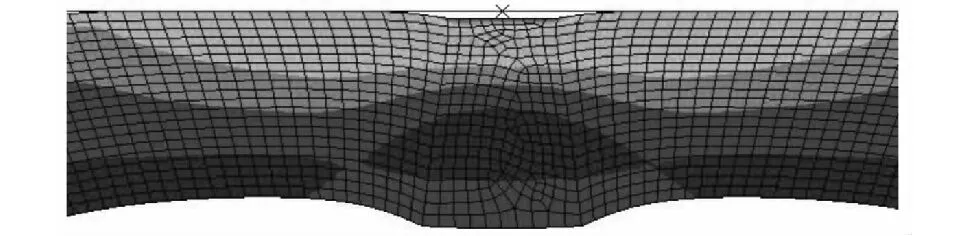
圖8 密封面空洞圖

4 結論

(1)通過有限元分析變形情況可知，“M”形充氣密封圈最大von-Mises應力主要出現在“M”形左右兩側內部圓弧面、頂部凹陷圓弧與門框接觸面處。因此，要選擇合適的倒角半徑，既保證有足夠的接觸應力，又不至于圈內應力長期過大使得工作壽命降低。

(2)法向接觸應力是保證密封效果的關鍵，該應力隨充氣壓力的增大而增大，接觸橫截面寬度也隨之增長，在外表面中間的凹陷圓弧部分達到應力峰值；被密封介質壓力使得靠近介質一側的接觸應力減小，接觸橫截面寬度變短；隨著密封間隙的增加，其內部接觸應力也相應增大。

(3)為了提升充氣圈的密封性能，需要結合密封圈的受力變形、環境溫度、環境壓力和材料特性等綜合進行結構設計，密封圈的表面還應做涂層防腐處理；選擇適當的密封介質壓力和充氣壓力比值，既能保證密封效果又能延長充氣圈的使用壽命。

(4)利用有限軟件ABAQUS對充氣密封圈進行仿真模擬和優化設計是可行的。

[1] Kotter M. DRY Fermentation-A New Method For Biological Treatment[J/OL].http://www.gtz.de/ecosan/download/CESMA2002-Koettner.pdf，2007-10-20．

[2] Kottner M. Anaerobic systems for biological treatment in ecosan[EB/OL].http://www2.gtz.de/dokumente/oe44/ecosan/cb/en-anaerobic-system-ecosan-biogas-fertilizer-2005.pd，2007-10-20．

[3] Zhang Ruihong. Developing a R.D.T Digester System with Built-In Flexibility [EB/OL]. http://www.jgpress.com/Energy05/Zhang_M.pdf，2008-01-28．

[4] 韓 捷, 向 欣, 李 想. 覆膜槽沼氣規模化干法發酵技術與裝備研究[J]. 農業工程學報, 2008, 24(10):100-104.

[5] 趙國明. 規模化干法沼氣發酵技術及裝備的研究與示范[D].長春：吉林大學, 2009.

[6] 孟祥鎧, 吳大轉, 王樂勤. 充氣密封的非線性有限元分析[J]. 潤滑與密封, 2007, 32(3): 110～112.

[7] 賁可存, 湯文成, 徐鴻翔. 充氣式柔性密封的非線性有限元分析[J]. 潤滑與密封, 2008, 33(3): 69～71.

[8] 周仕明, 李道奎, 唐國金. 充氣式自密封氣囊結構的非線性有限元分析[J]. 潤滑與密封, 2010, 35(10): 59～63.

[9] B N JPersson, O Albohr, C Creton, et al. Contact area between a viscoelastic solid and a hard randomly rough substrate[ J]. Journal of Chemical Physics, 2004, 120(18):8779 -8793.

[10] 王 偉, 鄧 濤, 趙樹高. 橡膠Mooney-Rivlin模型中材料常數的確定[J].特種橡膠制品,2004,25(4):8-10.

[11] Gent Alan N. Engineering with Rubber: how to Design Rubber Components[M]. Hanser Publishers, 2001.

[12] 付 平, 常德功. 密封設計手冊[M]. 北京: 化學工業出版社, 2009: 157-170.

Nonlinear Finite Element Analysis of Inflatable Seals in the Garage-type Dry Fermentation Tank /

LI Rui-rong1,2, ZHU De-wen1, WANG Peng-jun1, HAN Bo-he1, CHEN Ming-jiang1, CHEN Yong-sheng1/

( 1.Nanjing Research Institute for Agricultural Mechanization, Ministry of Agriculture, Nanjing 210014, China; 2.Key Laboratory of Development and Application of Rural Renewable Energy, Ministry of Agriculture, Chengdu 610041,China)

Based on nonlinearity finite element theory of large deformation and contact problem, a 2D plane finite element model of M-shaped inflatable seal was derived. The seal mechanism was analyzed and the distribution rule of normal contact stress along sealing surface was obtained. The influence of loading pressure, sealed pressure and sealing gap on normal contact stress were discussed. Results showed that the normal contact stress was important to assure a safety sealing, which increased with the increase of loading pressure, reaching the peak in the middle of outside surface, and the length of sealing surface increased as well. With the action of the sealing pressure, the normal contact stress on the side of sealing media was cut down and the length of sealing surface got shortened. With the increase of sealing gap, the normal contact stress also increased. To promote the sealing performance, the structure of inflatable seal needs to be designed according to the stress deformation, environmental temperature, sealing pressure and material properties. It is needed to add a corrosion resistant coating on the surface of seals. And it is crucial to choose the suitable ratio of sealing pressure and loading pressure, which could ensure the sealing effect and prolonging the life of inflatable seals.

inflatable seals; nonlinear finite element; M-shaped seals; silicon rubber

2015-10-27

2016-01-19

項目來源： 農業部農村可再生能源開發利用重點實驗室開放課題基金資助項目(2013009)； 江蘇省自然科學基金資助項目(BK20151073)

李瑞容，(1984-)，女，漢，江蘇南京人，助理研究員，主要從事農業廢棄物處理與資源開發技術研究工作，E-mail:lrr006@163.com

陳永生，E-mail:cys003@sina.com

S216.4

A

1000-1166(2016)02-0066-04