基于動態因子和共享適應度的改進粒子群算法
譚熠峰, 孫婷婷, 徐新民
(浙江大學 信息與電子工程學院, 浙江 杭州 310027)
表1 測試函數及其特點
表2 粒子數較多時算法的迭代對比
表3 粒子數較少時算法的迭代對比
?
基于動態因子和共享適應度的改進粒子群算法
譚熠峰, 孫婷婷, 徐新民*
(浙江大學 信息與電子工程學院, 浙江 杭州 310027)
為提高粒子群算法的收斂速度和優化性能,避免陷入局部最優,提出了一種基于動態學習因子和共享適應度函數的改進粒子群算法.在慣性權重w隨著迭代次數非線性減少而動態調整學習因子的基礎上,引入共享適應度函數.當算法未達到終止條件而收斂時,利用粒子和最優解間距離挑選一批粒子重新初始化形成新群體,并用共享適應度函數對新群體進行評價,新舊2個群體分別追隨自己的局部最優解直至迭代結束.對4個典型多峰復雜函數的測試結果表明,該改進算法不僅加快了尋得最優解的速度,而且提高了粒子群算法全局收斂的性能.
動態;學習因子;共享適應度;粒子群算法
0 引 言
粒子群算法(Particle Swarm Optimization, PSO)的基本概念源于對鳥群覓食行為的研究,最早用于模擬簡單的社會系統.與遺傳算法、蟻群算法等進化計算方法相比,PSO算法具有收斂速度快、設置參數少、程序實現簡潔方便等特點,可以解決大量非線性、不可微、連續多峰的優化問題,已廣泛應用于神經網絡訓練、函數優化和模糊系統控制等領域[1-4].但是,由于PSO算法在優化過程中追隨最優解,所有粒子趨向同一化,如果該最優解所在位置為一局部最優點,粒子群就難以跳出局部最優,出現早熟收斂現象.
為了克服標準PSO算法早熟收斂的缺點,GANDOMI等[5]提出了混沌增強型PSO算法,WANG等[6]提出通過增加變異算子改進PSO算法,張健等[7]提出了動態約束因子法(Dynamic Constrain Factor PSO, DCF-PSO).這些改進算法明顯提高了收斂的速度,但在局部收斂方面收效甚微.本文在改進動態調整學習因子的基礎上,引入遺傳算法中的共享適應度函數,每當算法陷入局部最優時,根據海明距離對部分粒子重新初始化,并用共享適應度函數來評價新粒子群,對舊粒子群則通過調整學習因子方法達到快速精確搜索.通過經典測試函數結果表明,該改進在加快算法收斂速度的同時,大大提高了全局收斂的成功概率.
1 標準粒子群和動態約束因子算法
1.1 標準粒子群算法
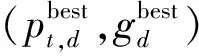

(1)
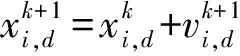
(2)

1.2 動態約束因子算法
為了改進標準粒子群算法,避免粒子群算法過早收斂,根據進化算法在運行初期需加強全局搜索解空間能力,后期需要細化解空間開拓能力的特點,文獻[7]提出了一種根據慣性權重值w的非線性遞減動態調整學習因子c1和c2的DCF-PSO.該算法中w和c1、c2分別按式(3)與(4)更新:
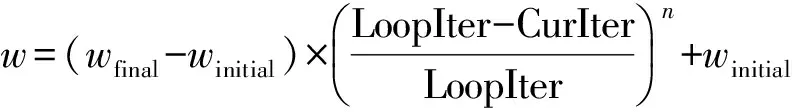
(3)
c1=c2=0.5w2+w+0.5,
(4)
其中,wfinal和winitial分別為w的最大值和最小值,LoopIter表示最大迭代次數,CurIter表示當前迭代次數,n是冪級數.
實驗結果表明,該改進有效提高了粒子群算法的收斂速度,但其全局收斂性能未能明顯提高.
2 改進的PSO算法
2.1 共享函數
GOLDBERG等[9]在遺傳算法中提出用共享函數度量2個個體的相鄰關系和程度.給定個體g,其共享函數由其與種群中其他個體的關系決定,每個個體有一個共享函數值Si,i=1,2,…,P,則個體的原適應度函數f(i)可調整為新的適應度函數f(i)new:

(5)
文獻[10-11]提出了基于共享函數改進型粒子群優化算法(Fitness Sharing Particle Optimizer, FSPSO).該算法初期同標準PSO,當粒子群陷入局部最優或暫時停滯狀態時,隨機選擇部分粒子重新初始化為一個新群體,同時保留部分作為舊群體用于繼續搜索局部最優.2個群體在各自最優個體gbest下更新和搜索.新群體利用給定共享半徑dshare得到的共享適應度函數阻止新群體立刻回到局部最優.該算法能達到跳出局部最優的目的,但速度比標準算法低.
2.2 改進的粒子群算法
為同時提高標準全局版PSO的收斂速度和全局收斂性,保證群體多樣性的存在,防止算法過早成熟,結合文獻[7]中的DFC-PSO和文獻[10]中的FSPSO,提出了帶有動態學習因子和共享適應度函數的粒子群算法.
在算法迭代早期,利用式(1)與(2)動態調整w和c1、c2,更新粒子的速度和位置.
當粒子群陷入局部最優時,對部分粒子重新初始化形成新群體.由于舊群體用于在早熟區繼續尋找最優,因此越接近最優位置越好,本文將與早熟區最優解之間距離較近的粒子作為舊群體,分布較為分散的部分粒子則進行變異,再次初始化.給定個體xi,其與種群已找到的最優位置xg間的距離shi由海明距離決定:
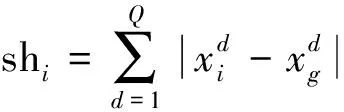
(6)
假定有一個8個粒子的群體在某一時刻局部收斂到位置xg,如圖1左圖所示,且sh8>sh6>sh7>sh1>sh4>sh5>sh3>sh2,按海明距離值的大小順序,取出占粒子總數前75%(即6個)的粒子作為新群體變異.保留位置較為集中的2個,構成一個獨立的舊群體,繼續搜索早熟區的最優解gbest.

圖1 粒子群分布圖Fig.1 Distribution of a particle swarm
為更好地搜索到最優解,本文按粒子類別分類調整學習因子.由于新群體被初始化,按式(3)與(4)計算w更新粒子,其中式(3)中分母上的迭代總數LoopIter變為LoopIternew,LoopIternew為剩下還未發生的迭代總次數,以保證w重新從wfinal遞減至winitial.而舊群體用于追隨最優解,因此早熟區粒子的慣性權重w和認知學習因子c1繼續減小,而用于追隨最優解的社會學習因子c2:
c2=4-c1.
(7)
則按式(7)調整,以便增大粒子的社會學習信息,尋得早熟區最優解.
然而,新群體中的粒子也可能再次進入早熟區,如圖1右圖中的粒子x6.為阻止粒子在迭代過程中再次陷入同一最優點,參照文獻[10]利用共享距離dshare對新個體的適應度進行調整.本文根據粒子群的分布關系采用動態計算方法改變dshare.在初始化之前,根據shi的大小,以dshare=shm作為早熟區的判斷條件,其中shm為占粒子總數百分比為m的粒子的距離.在圖1中當m=25%時,dshare為粒子x3到最優解的距離.重新初始化后,計算新群體中粒子到早熟區最優解的距離d_deci,若d_deci (8) 其中M為增強適應度的一個常數,取值1 000. 可見若新粒子進入早熟區,越靠近收斂中心其 對于粒子群是否陷入局部最優,可借鑒文獻[12]中使用的判斷方法,當gbest和每個粒子的pbest均值分別連續,T1和T2迭代最優值沒有得到提升,則選擇部分粒子重新初始化. 算法具體步驟如下: 1)對粒子的位置和速度進行隨機初始化; 2)分別計算粒子的適應度,判斷迭代次數是否超過最大值,若是則跳至步驟6,否則繼續; 3)判斷粒子群是否收斂,若是則跳至步驟5,否則繼續; 4)按算法動態更新約束因子,更新每個粒子的位置與速度,跳至步驟2; 5)計算海明距離值shi及共享距離dshare,選出部分粒子重新初始化,跳至步驟2; 他們的通話內容如下:“老公,是不是我想要什么你都會給我啊?”“那當然。”“我要星星。”“你養仙人球都死,還養猩猩?一頭猩猩多少錢?”“不是,我要天上的星星!”“這個啊……晚上回家帶你看。” 6)迭代停止,得到最優解. 2.3 改進實驗結果 為了說明改進的有效性,在Dell-T7500、操作系統為Windows8、所用仿真軟件Matlab版本為R2013a的環境下,將標準PSO、n=1.2的DCF-PSO與FSPSO以及本文算法進行對比.其中wfinal=1.0,winitial=0.3,變異比例l=0.6,對固定系數的算法選擇c1= c2=2,w=0.729.為更好地對上述算法進行評估,避免算法性能表現出偶然性,采用4個經典多峰函數Griewank、Rastrigin、Ackley及Schaffer為適應度評價函數,這些函數存在大量局部最優值,很難從中找到全局最優值,是評估算法性能的理想函數,各測試函數的特點如表1所示. [8,11,13],表2列出了當Griewank、Rastrigin、Ackley粒子數為53、Schaffer粒子數為8時,算法的迭代條件及運行結果.同時作為對比,表3列出了當粒子數減少,Griewank、Rastrigin、Ackley粒子數為30、Schaffer粒子數為5時算法的迭代條件及運行結果.其中Ps表示成功收斂到最優解的次數,Tave表示達到門限值時的平均迭代次數. 表1 測試函數及其特點 Table 1 Test functions and their characters 表2 粒子數較多時算法的迭代對比 Table 2 Performance comparison of algorithms with more particles 表3 粒子數較少時算法的迭代對比 Table 3 Performance comparison of algorithms with fewer particles 由表2可知,當粒子數較多時,DCF-PSO的收斂速度明顯提高,但其全局收斂性與標準PSO無明顯差異;FSPSO的全局收斂性更好,搜索到最優解的次數增加,但其收斂速度與標準PSO幾乎一致.DCF-PSO動態調整學習因子使得算法在不同時期有不同的搜索能力和速度,提高收斂速度的同時不至于經常陷入局部最優;FSPSO始終保證粒子群體的多樣性,能夠及時從局部最優狀態中跳出,從而提高了全局收斂性. 改進算法結合了DCF-PSO和FSPSO的優點,相對于前述3種算法,其全局收斂性明顯增強,成功搜索到最優解的次數Ps大大增加,幾乎每次都能收斂到最小值;同時與前3種算法相比,改進算法的平均收斂次數更少,收斂速度提高很多,且均優于單獨改進的DCF-PSO或FSPSO. 由表3可知,當粒子數較少時,各算法成功收斂到最優解的次數都有明顯降低,速度變慢.DCF-PSO和FSPSO與標準PSO相比,其性能與粒子數較多時一致,改進算法相較于前述3種算法,全局收斂性明顯變好,優于單獨改進的DCF-PSO或FSPSO,但其收斂速度與DCF-PSO比無顯著變化,比標準PSO和FSPSO要快. PSO算法是一種實現容易、精度高、收斂快的進化優化算法.本文在慣性權重隨著迭代次數減小、動態改進學習因子的基礎上,引入遺傳算法中的共享適應度函數.在運算過程中,隨著算法收斂選擇部分粒子的初始化,將粒子群變異為新舊2個群體后進一步搜索全局最優解,通過動態共享距離阻止新群體回到舊群體的局部最優值.該改進算法相對于標準PSO計算量并未顯著增加,對經典多峰復雜函數的仿真實驗表明:該算法在不同粒子數量下均表現出更好的性能,具有很強的適應性,不僅加快了其尋得最優解的速度以及收斂速度,而且增強了粒子群算法全局收斂的性能. 參考文獻(References): [1] 龍泉,劉永前,楊勇平.基于粒子群優化BP神經網絡的風電機組齒輪箱故障診斷方法[J].太陽能學報,2012,33(1):120-125. LONG Quan, LIU Yongqian, YANG Yongping. Fault diagnosis method of wind turbine gearbox based on BP neural network trained by particle swarm optimization algorithm[J].Acta Energiae Solaris Sinica,2012,33(1):120-125. [3] 王登科,李忠.基于粒子群優化與蟻群優化的云計算任務調度算法[J].計算機應用與軟件,2013,30(1):290-293. WANG Dengke, LI Zhong. A task scheduling algorithm based on PSO and ACO for cloud computing[J]. Computer Applications and Software,2013,30(1):290-293. [4] KHARE A, RANGNEKAR S. A review of particle swarm optimization and its applications in solar photovoltaic system[J]. Applied Soft Computing,2013,13(5):2997-3006. [5] GANDOMI A H, YUN G J, YANG X S, et al. Chaos-enhanced accelerated particle swarm optimization[J]. Communications in Nonlinear Science and Numerical Simulation,2013,18(2):327-340. [6] WANG G G, GANDOMI A H, YANG X S, et al. A novel improved accelerated particle swarm optimization algorithm for global numerical optimization[J]. Engineering Computations,2014,31(7):1198-1220. [7] 張健,朱旭東,王真.一個新的動態約束因子PSO算法[J].河北工業大學學報,2010,39(003):51-55. ZHANG Jian, ZHU Xudong, WANG Zhen. A new dynamic constrain factor particle swarm optimization algorithm[J]. Journal of Heibei University of Technology,2010,39(3):51-55. [8] KENNEDY J. Particle Swarm Optimization[M]// SAMMUT C, WEBB G I. Encyclopedia of Machine Learning. New York: Springer US,2010:760-766. [9] GOLDBERG D E, RICHARDSON J. Genetic algorithms with sharing for multimodal function optimization[C]// Proceedings of the Second International Conference on Genetic Algorithms on Genetic Algorithms and Their Application. Hillsdale: L Erlbaum Associates Inc,1987:41-49. [10] LI T, WEI C, PEI W. PSO with sharing for multimodal function optimization[C]//Proceedings of the 2003 International Conference on Neural Networks and Signal Processing, 2003. Nanjing: IEEE,2003(1):450-453. [11] 白瑞林,王利峰.一種基于共享法的改進型粒子群優化算法[C]//2005中國控制與決策學術年會論文集(上).沈陽:東北大學出版社,2005:795-798. BAI Ruilin, WANG Lifeng. A modified particle swarm optimization algorithm based on sharing method[C]//Proceeding of 2005 Chinese Control and Decision Conference. Shenyang: Northeastern University Press,2005:795-798. [12] 劉衍民,隋常玲,牛奔.解決約束優化問題的改進粒子群算法[J].計算機工程與應用,2011(12):23-26. LIU Yanmin, SUI Changling, NIU Ben. Improved particle swarm optimizer for constrained optimization problems[J]. Computer Engineering and Applications,2011(12):23-26. [13] 鄔嘯.一種對粒子群算法慣性權重的改進[J].計算機時代,2010(10):25-27. WU Xiao. An improvement for inertia weight of particle swarm optimization[J]. Computer Era,2010(10):25-27. [14] 周飛紅,廖子貞.自適應慣性權重的分組并行粒子群優化算法[J].計算機工程與應用,2014,50(8):40-44. ZHOU Feihong, LIAO Zizhen. Grouping parallel particle swarm optimization algorithm with adaptive inertia weight[J]. Computer Engineering and Applications,2014,50(8):40-44. TAN Yifeng, SUN Tingting, XU Xinming (CollegeofInformationScience&ElectronicEngineering,ZhejiangUniversity,Hangzhou310027,China) A modified particle swarm optimization algorithm based on dynamic learning factors and sharing method. Journal of Zhejiang University(Science Edition), 2016,43(6):696-700 To improve the global convergence ability and rate of particle swarm optimization, an improved particle swarm optimization algorithm based on dynamic learning factors and sharing method is proposed. The inertia weight factor of the algorithm decreases non-linearly, and the learning factor changes dynamically with the descending. A sharing fitness function is introduced on the basis of dynamic regulation. When the algorithm is stagnated without reaching termination, part of the particles will be selected according to the distance between particles and optimal solution. The chosen particles will be re-initialized as a new swarm and be evaluated by sharing fitness. The old and new swarms follow their own local solutions respectively until the end of the iteration. Simulation results of four typical multimodal functions show that the modified algorithm can greatly enhance the rate of the optimal solution searching and improve the global convergence performance of PSO. dynamic; learning factor; sharing fitness; particle swarm optimization 2014-03-04. 浙江省公益技術研究工業項目(2015C31073). 譚熠峰(1991-),ORCID:http://orcid.org/0000-0003-1151-9206,男,碩士研究生,主要從事嵌入式研究. *通信作者,http://orcid.org/0000-0002-0910-2375,E-mail:xuxm@zju.edu.cn. 10.3785/j.issn.1008-9497.2016.06.014 TP 301.6 A 1008-9497(2016)06-696-05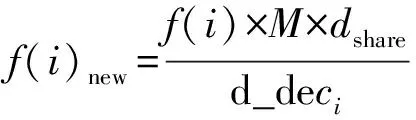




3 結 論


