系統集成商多階段產能預訂模型研究

張子為， 尚翠娟

(河北工業大學 經濟管理學院，天津 300401)

?

系統集成商多階段產能預訂模型研究

張子為， 尚翠娟

(河北工業大學 經濟管理學院，天津 300401)

隨著經濟全球化迅猛發展，系統集成商在運營組織變革中脫穎而出。系統集成商面對不確定需求需要快速做出響應，這就要求其集中智能化組織上游供應商的產能。本文基于供應鏈產能預訂機制和契約協調理論，構建了兩級供應鏈多階段需求下的產能預訂模型。用時域滾動執行法求解模型并進行敏感性分析，驗證了模型的有效性。為系統集成商做出產能預訂決策提供了有力依據。

系統集成商；多階段；產能預訂；契約

一、引言

信息化和經濟全球化的迅速發展，推動了運營組織變革。系統集成商(System Integrator，以下簡稱集成商)是指能為客戶提供系統集成產品與服務的專業機構，分散產能的集中智能化組織是其本質特征。集成商和供應商之間的長期契約可以有效控制物流和生產系統，從而提升競爭優勢。在長期契約執行過程中，集成商對運營安排和資源整合方案進行調整，以應對訂單需求波動帶來的風險。隨著不確定風險持續加大，有效的供應鏈產能預訂機制是集成商合理安排資源的關鍵方法。

以往有關供應鏈產能預訂的研究主要集中在以下4個方面。一是運用包括數量折扣[1]、收入共享[2]和回購契約[3]等傳統契約的研究，主要集中在單階段一對一報童問題，解決了單階段供應商產能協調問題。二是將產能預訂契約和其他類型契約結合以實現供應鏈協調。Jin和Wu[4]在產能預訂契約的基礎上結合預付費用形式，建立了可抵扣預訂費契約；孔融[5]將批發價格契約與產能投資分擔契約結合，研究了單階段供應鏈協調問題。三是由單階段模型擴展而來的多階段預訂模型研究，Serel[6]證明了相比于傳統價格契約，一個制造商和一個供應商之間的多階段產能契約可以增加產能利用率；Xu等[7]研究了多階段動態供應契約問題，其中買方每個階段從供應商訂購產品并且供應商允許其支付罰款來取消部分訂單；Inderfurth K, Kelle P和 Kleber R[8]在多階段預訂模型中考慮需求和現貨市場價格的不確定性；以上研究解決了多階段的靜態和動態產能預訂問題，但是沒有考慮多個異質供應商。三是Park S I和Kim J S[9]站在買方視角建立了對多個擁有不同能力和價格的供應商的多階段產能預訂模型。由于集成商負責整個生產服務過程，所以預訂供應商產能的過程是根據訂單工藝流程在多個供應商之間有序進行的，Park S I和Kim J S建立的模型考慮了一對多的供應鏈結構，但是沒有考慮有序預定過程并且模型中供應商生產提前期都在單個預訂周期內，無法適用于本文系統集成商的產能預訂過程。本文在Park S I和Kim J S研究的基礎上針對多個負責不同工序的異質供應商建立多階段有序產能預訂模型。

本文余下部分安排如下：第二節提出本文研究問題并進行模型假設。第三節，將產能預訂方法和數量彈性契約相結合，在由多個供應商構成的復雜供應鏈系統中構建多階段隨機需求的集成商產能預訂模型。第四節運用基于線性規劃的時域滾動執行方法(RIMS)對模型進行仿真求解，分析參數對模型結果的影響，驗證所構建模型的有效性。第五節總結本文研究成果，并分析局限性以及未來的研究方向。

二、問題描述與假設

本文模型研究的集成商產能預訂過程分為兩個步驟。第一步，在計劃期初期，此時需求信息未知，集成商根據由工藝流程產生的預訂計劃有序向供應商提供預訂其產能的預訂單，供應商根據預訂單和自身的風險意識決策其產能準備量。第二步，集成商觀察到需求市場的真實需求信息后，采用完全信息更新的方式，在供應鏈契約基礎上確定最終的采購訂單，供應商根據最終訂單組織生產，當從供應商處獲得的產品不足以滿足市場需求量時，集成商還可以從現貨市場采購產品。集成商產能預訂過程模型如圖1。

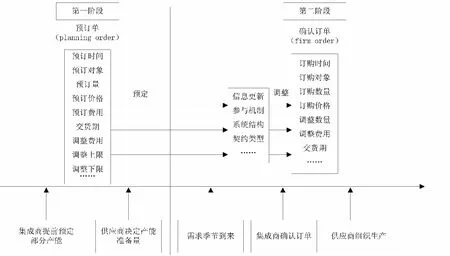
圖1 系統集成商產能預訂過程模型

假設在該模型中，包含一個集成商和多個異質供應商，每個供應商在約定期限內向集成商提供生產一定數量產品的產能，供應商之間的預訂過程是有序的，集成商在制定預訂計劃時便根據需求預測工藝流程進行了工序分解，即預訂順序是給定的。產能量在初期根據各個供應商之前的訂單來確定。在當前階段開始時，集成商有機會修正先前提供給每個供應商的訂單數量，確定最終的訂單量。同時，集成商可以根據契約來修正未來某階段的預訂量。

本文站在集成商對供應商集中控制角度下，研究如何確定集成商對每個供應商的當前階段采購量、后續階段預訂量以及現貨市場采購量以使得自身總成本最小，集成商成本主要包括采購、庫存成本、訂單變動成本等其他相關成本。本文所提出的模型中，計劃期很長(通常1-2年)，此時間框架下，每個供應商的提前期可以為每個階段的整數倍。

三、建立系統集成商多階段產能預訂模型

(一)參數設置

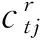
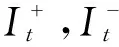
(二)關于有序預訂過程

集成商根據訂單工藝流程和供應商的供應水平，將多周期內的生產任務對供應商有序安排，即在整個預訂周期內，供應商并不是一直被預訂產能，而是間斷的進行生產，所以本文引入一個T×J的01矩陣，矩陣中0代表此階段內未對該供應商進行產能預訂，1則代表進行了預訂，此矩陣作為模型的固定參數進行初始化。

(三)約束條件

不失一般性，由階段1的初始量、預訂量和現貨購買量之和等于階段1的補給水平得：

(1)

當集成商最終訂單量與初始預訂量有差別時，供應商的成本就會增加。因此，供應商通常會設定一個允許的調整范圍。調整增加時的約束為：

(2)

調整減少時，約束為：

(3)

從階段2到T，補給水平要達到初始庫存、每個供應商交付的計劃訂單與此階段向現貨市場采購量之和。輸入-輸出之間的關系如式(4)所示(L表示Lj)：

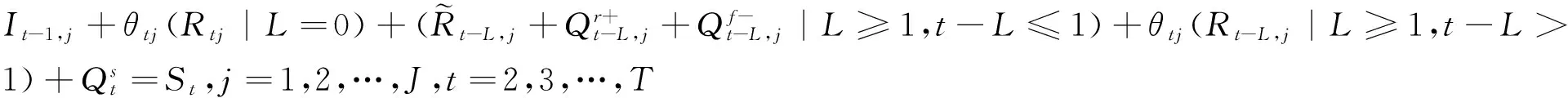
(4)

式(4)第一項是階段t開始時的初始庫存。第二、三項代表階段t開始時期望到達的訂單量。其中，第二項是提前期為0的訂單。第四項是階段2到T-1之間確定的預訂量，在一定提前期之后期望實現階段t的需求。

在每個階段開始和結束時的庫存水平，表示為：

St-dt=It，t=1,2,…,T。

(5)

因為供應商不可能短期內增加產能，所以存在預訂量上限。

Rtj≤utj,j=1,2,…,J，t=2,3,…,T。

(6)

當集成商頻繁的變更預訂量時，相應的供應商就必須頻繁的調整他們的生產計劃，因此供應商會對未來每個階段的預訂變更設定一個限制。對變更的約束表示為：

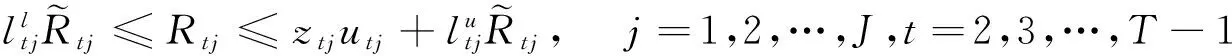
(7)

ztjutj項為除了先前預訂量之外，允許的最小預訂量。如果沒有這個緩沖機制，在未來某階段先前預訂量為0后，此階段的預訂量也會變為0。

本文中采用客戶訂單滿足率作為評價標準，將訂單滿足率定義為需求的滿足比例，滿足標準正態分布的條件分布特性。為了生成訂單滿足率的相關約束，將安全庫存水平E(It)設定為kσt。當未來t階段的需求預測誤差(用εt表示)滿足εt≤kσt時，階段t末期的期望庫存水平為正值，如式(8)所示。

E(Stj-dtj)=E(Stj-ftj-εtj)=kσtj-εtj>0

(8)

庫存量滿足目標訂單滿足率的約束如下。

Itj≥kσtj,j=1,2,…,J，t=1,2,…,T。

(9)

(四)目標函數

本文以集成商總成本最小為目標函數，如前面流程描述，集成商的相關成本包括庫存持有成本、采購成本、改變訂單的懲罰費用成本和預訂產能的預訂費用。

整個計劃期內的期望庫存成本為

(10)

階段1的采購成本等于當前階段中考慮提前期時到達的最終訂單和從現貨市場采購的成本之和。

(11)

未來階段中的期望采購成本等于每個供應商預訂成本與現貨市場采購成本之和：

(12)

假設預訂費用是基于當前階段新預訂量按比例支付的，轉化為線性形式如下：

(13)

其中公式(14)：

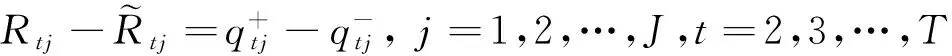
(14)

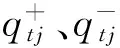
當取消預訂量時，供應商通常會退還給集成商一部分預訂費用。同理得公式(15)：

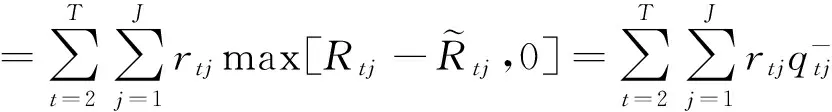
(15)

相鄰階段中訂單量的顯著改變會使供應商改變生產計劃來應對訂單的波動，同樣也會導致成本增加。這時，供應商會收取一定的懲罰費用。轉化為線性形式如下：

(16)

此時需要增加下面的約束：

(17)

計劃期內集成商期望總成本折現后，用DI表示，目標函數如下：

(18)

四、模型求解方法

本文模型是基于最優化理論的線性規劃模型，應用滾動時域方法(Rolling-horizonImplementationforMultipleSuppliers)求解模型，滾動時域計劃是供應鏈契約在生產計劃和多周期協調中應用最廣的方法[10]，基于線性規劃的滾動時域執行方法流程如下。

Step1: 初始化

Step1.1 令當前階段為階段1; 將當前庫存水平重置為I0。

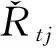
Step2: 運行線性規劃模塊

預測需求ft,t=1,2,…,T; 運行線性規劃模塊。

Step3: 輸出

Step4: 等待一個階段的運行

Step5: 新計劃階段的輸入

Step5.1 將當前庫存水平重置為I0。

Step 5.3 令t←1，轉到Step 2.

五、算例分析

本節算例考慮一年計劃期，每個階段為4周，即該算法需要計算12個階段的決策(假設一個月包括4周)。

此算例分為兩部分：常規測試和敏感性分析。常規測試中將RIMS的結果與開環方法(OPEN-LOOP:OM)結果比較，開環方法不是基于滾動操作，而是在初始時運行整個計劃期的線性規劃，最終輸出整個計劃期的線性規劃結果。

(一)已知模型數據

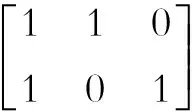
預測需求均值函數如下得到：

由于本算例的計劃期為1年，本文研究的產品為季節性產品，一年中產品的平均需求滿足產品生命周期理論，預測需求均值函數的表達式為：um=-D×(α×M)-2×(m-α×M)2+D，其中總計劃期長度M=12月；最大需求量D=500；α=0.83為最大需求系數；m為計劃期下標。

預測偏差滿足：

(19)

其中，ρα為需求均值的白噪聲標準差，設置為0.2。

本節算例使用MATLAB 2013b進行編程和運行，將以上的數據輸入程序中，得出該模型的最優決策和目標函數值。

表1 集成商相關輸入參數

表2 分散決策中集成商采購價格數據

表3 供應商屬性

注：U表示計劃期內每個階段的需求預測均值。

表4 供應商成本相關參數

(二)模型計算結果

由輸入模型的參數求解得到結果，多供應商的滾動時域執行方法所得結果為1 669 283.938，開環方法所得結果為1 877 944.430 25，高出12.5%的成本數量，可見本模型能為減小集成商節約較大的總成本。OM機制成本較高的原因是其不適應更新的預測信息，造成預訂的產能過剩或不足，產生了額外成本。

(三)敏感性分析

下面對模型參數進行敏感性分析，分析參數值的不確定性對目標函數的影響。輸入的變化參數為集成商單位采購價格、單位現貨市場價格。如圖2和圖3。

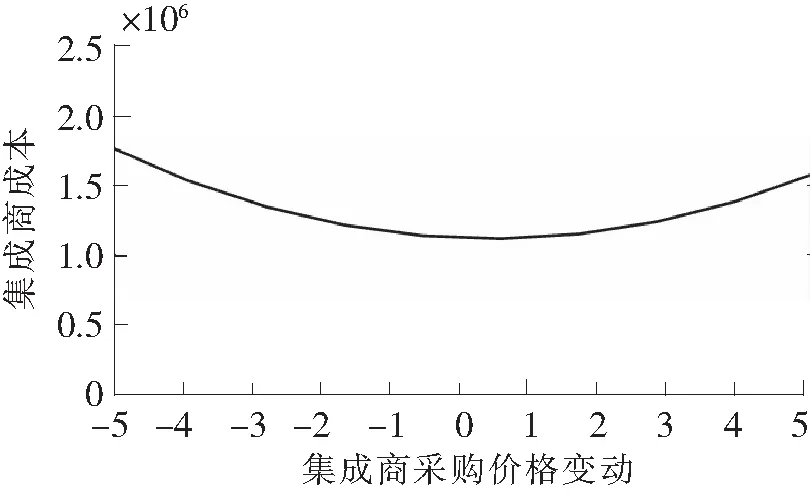
圖2 集成商單位采購價格敏感性分析圖

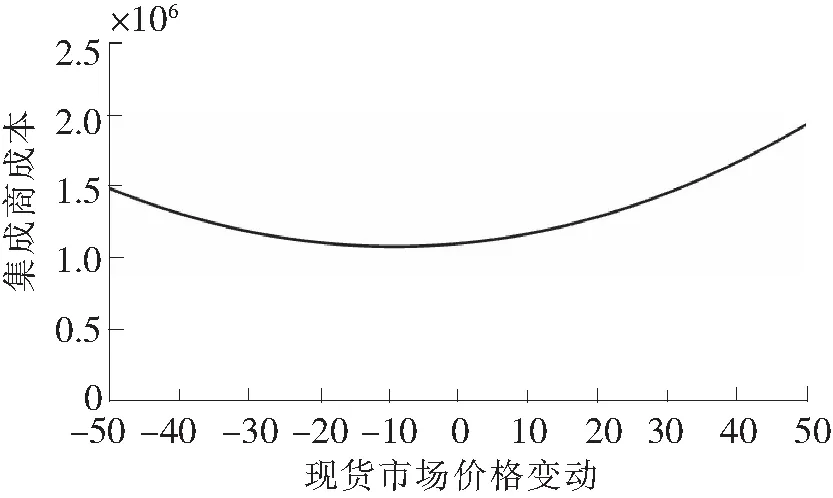
圖3 現貨市場單位價格敏感性分析圖

圖2橫軸為參數變化值，縱軸為集成商總成本值。由圖2可以看出，隨著集成商采購價格的由小到大變化，集成商成本值呈現先減小再增大的曲線，并且最低點出現在0點右側，說明當單位采購價格小幅增加時集成商能獲得最低成本。由圖3可以看出，曲線最低點在0點左側，說明當現貨市場價格減小為90時集成商的成本最小。

通常的協調模型中需求波動一般不考慮銷售價格對模型的影響，但在實際市場中，銷售價格往往是影響銷售量非常關鍵的一個參數。本文下一步探討價格系數對預訂模型的影響。

在5.1中需求函數構造的基礎上，將需求函數dt=um+εt中的需求均值調整為：um(p)=um-βp′,其中價格敏感系數β∈[0,1],p′∈[-50,50]為價格的變化區間。分析結果如圖4。

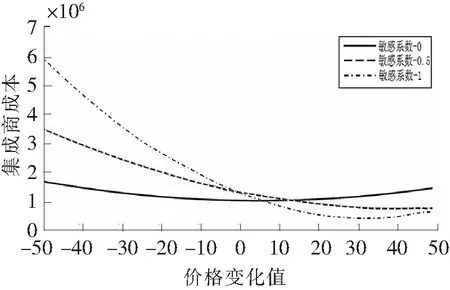
圖4 價格敏感系數對模型的影響

圖4表明，當銷售價格上升30時，該模型針對需求敏感系數較大的產品能獲得最低的集成商成本，所以該模型能很好的適應需求對價格高度敏感的產品供應鏈。

本章通過第二節得出模型的求解結果優于傳統開環求解方法，驗證了求解模型的有效性。第三節對模型參數集成商單位采購價格和單位現貨市場價格進行分析得出二者的敏感性變化趨勢，以及模型結果最優時對應的參數設置。最后分析價格敏感系數對模型的影響，結果表明該模型能很好的適應需求對價格高度敏感的產品供應鏈。

六、總結與展望

隨著需求變化速度加快，針對日益嚴峻的產能集中智能化組織問題，本文提出了集成商和多個異質供應商之間的多階段產能預訂模型，運用了多供應商滾動時域執行方法(RIMS)進行線性規劃求解，通過與其他方法得出的最優解對比證明了模型的有效性，并對多個模型參數進行了敏感性分析。本文的模型為集成商在面對不確定性需求時快速進行產能預訂決策提供了有力工具。該模型可以有效降低集成商成本并且運行簡單迅速，使其對供應商產能高效利用以降低自身運營成本具有十分重要的現實意義。

本文站在集成商的角度考慮減小成本問題，沒有全面考慮供應商視角，進一步的研究可以加入供應商在產能預訂問題上的最優決策，變為買方-賣方問題。本文的假設條件是加工順序是給定的，未來可以將工藝流程分解過程與該模型融合。另外，本文沒有考慮現實中存在的突發情況下供應商供應中斷問題，如何協調能使得突發情況造成的經濟損失最小也是進一步研究的方向。

[1]曹宗宏,周永務.價格和庫作量影響需求的供應鏈量折扣定價模型[J].系統工程學報, 2008, 23(1): 67-73.

[2]但斌,徐廣業.隨機需求下雙渠道供應鏈協調的收益共享契約[J].系統工程學報, 2013, 28(4): 514-522.

[3]趙泉午,熊榆,林婭，等.多個零售商庫存競爭的易逝品回購合同研究[J].系統工程, 2004, 22(8): 39-42.

[4]Jin M Z, Wu S D. Capacity reservation contracts for high-tech industry [J]. European Journal of Operational Research, 2007, 176: 1659-1677.

[5]孔融,董明,劉少軒.考慮產能投資分擔的供應鏈契約協調研究[J].上海交通大學學報, 2012, 12(46): 1994-1999.

[6]Serel D A. Capacity reservation under supply uncertainty [J]. Computers & Operations Research, 2007, 34: 1192-1220.

[7] Xu N. Multi-period dynamic supply contracts with cancellation[J]. Comput. Oper. Res. ，2005，32：3129-3142.

[8] Inderfurth K, Kelle P, Kleber R. Dual Sourcing Using Capacity Reservation and Spot Market: Optimal Procurement Policy and Heuristic Parameter Determination[J]. European Journal of Operational Research, 2013, 225(2):298-309.

[9] Park S I, Kim J S. A mathematical model for a capacity reservation contract[J]. Applied Mathematical Modelling, 2014, 38(38):1866-1880.

[10]Zhu X. Replenishment strategy and coordination with quantity flexibility in a rolling-horizon environment [M]. Hong Kong University of Science and Technology: Dissertation, 2006.

[11]Boulaksil Y, Grunow M, Fransoo J C. Capacity flexibility allocation in an outsourced supply chain with reservation [J]. International Journal of Production Economics, 2011, 129(1): 111-118.

Research on the Multi-stage Capacity Reservation Model of the System Integrator

Zhang Ziwei, Shang Cuijuan

(School of Economics and Management, Hebei University of Technology, Tianjin, 300401,China)

With the rapid development of economic globalization, system integrators in the operation of organizational change stand out. System integrators need to respond quickly in face of the uncertainty of demand, which requires the organization the capacity of upstream suppliers centrally and intelligently. Based on the supply chain mechanism and the coordination theory of capacity reservation contract, we constructed a model of two levels, which can satisfy the multi-stage demands. A rolling-horizon implementation strategy and sensitivity analysis were suggested for the efficient application of the model. It provided a sound basis for the system integrator to make the decisions of capacity reservation.

system integrator; multi-stage capacity; reservation; contracts

2095-0365(2016)04-0011-07

2016-08-31

張子為(1991-),男,碩士研究生,研究方向：物流與供應鏈管理。

C393

A

10.13319/j.cnki.sjztddxxbskb.2016.04.02

本文信息:張子為，尚翠娟.系統集成商多階段產能預訂模型研究 [J].石家莊鐵道大學學報：社會科學版，2016，10(4)：11-17.