一道拋物線定點問題的奇妙變題及推廣

江蘇省興化市第一中學 (225700)

葛新燕

?

一道拋物線定點問題的奇妙變題及推廣

江蘇省興化市第一中學 (225700)

葛新燕

一、奇妙的變題

問題 過拋物線y2=2px的頂點O作互相垂直的直線OA,OB與拋物線相交于另兩點A,B，求證：直線AB經過定點(2p,0)．

本題是一道常見的拋物線習題，以此題作為題根而編制的試題比比皆是．一種有趣的思考是：作點B關于x軸的對稱點B′，那么直線AB′是否仍然經過定點呢？通過幾何畫板進行實驗，驗證了這一猜想的正確性，并發現定點為(-2p,0)．這一有趣的事實激發了筆者的探索欲望．

由于原題中OA,OB互相垂直，所以它們的斜率積為-1．相對于原題，此時直線OA,OB′有何特征呢？考察OA,OB′的斜率，發現關系并不明顯．轉換思維角度，從傾斜角的角度考察發現，直線OA,OB′的傾斜角之和為90°，從而斜率積為1．下面，從傾斜角和為90°這一角度敘述該變題．

定理1 過拋物線y2=2px的頂點O作直線OA,OB與拋物線相交于另兩點A,B，若直線OA,OB的傾斜角之和為90°，則直線AB過定點(-2p,0)．

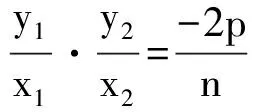
二、問題的縱向推廣

定理1的條件具有極大的自由度，發展空間很大；另一方面，有力的方法不僅使原問題獲得了簡解，也為我們進一步研究問題打開了思路．

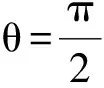
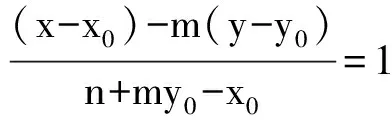
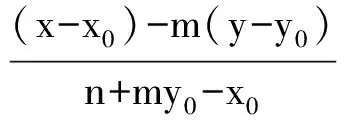
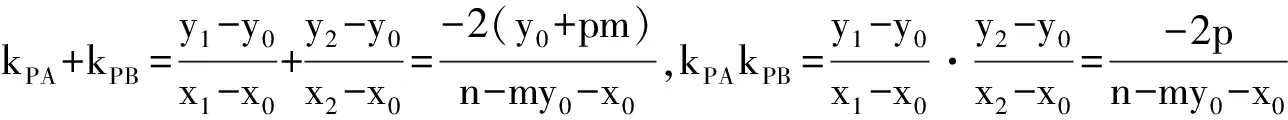
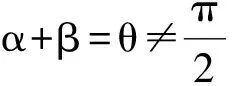
三、問題的橫向推廣

拋物線是圓錐曲線的一種，它和橢圓、雙曲線有著割舍不斷的血緣關系，因此，我們自然會思考：橢圓和雙曲線中是否也存在類似的定點呢？

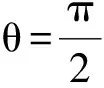
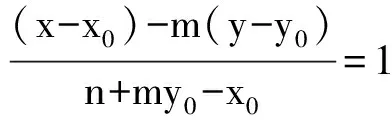
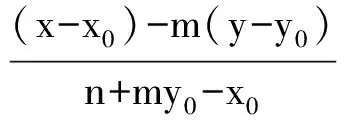
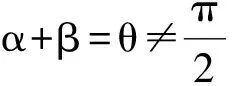
說明：當u>0,v>0,u≠v時，ux2+vy2=1表示橢圓；當uv<0時，ux2+vy2=1表示雙曲線．

四、問題的統一推廣

從成功的喜悅中抽出身來，回到起點，將原題和變題進行比較發現OA,OB的斜率之積分別為-1,1，都是定值，從這個角度，我們可將它們統一推廣為(證明略)：

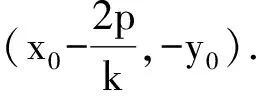
類似的，我們有：

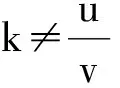
我們從一道常見的拋物線定點問題出發，由淺入深，由此及彼，動中尋靜，探索發現了圓錐曲線中一組耐人尋味的定點．無序的運動中蘊藏著靜態的結果，這是數學的精彩和魅力，數學之美妙著實令人如癡如醉．