基于旋量理論的混聯采摘機器人正運動學分析與試驗

陽涵疆，李立君，高自成

（中南林業科技大學機電工程學院，長沙 410000）

基于旋量理論的混聯采摘機器人正運動學分析與試驗

陽涵疆，李立君※，高自成

（中南林業科技大學機電工程學院，長沙 410000）

為滿足油茶果機械化、自動化采摘的要求，避免利用傳統的Denavit-Hartenberg(D-H)參數法對機器人進行運動學分析時的缺陷，提出了一種基于旋量理論構建混聯采摘機器人運動學方程的方法。根據混聯采摘機器人機械臂的結構特點進行簡化；基于所提出的方法建立了機器人正運動學方程，獲得末端執行器的位置正解；隨機選取5組關節變量值，得出末端執行器在基礎坐標系各坐標軸上的最大絕對位置誤差為10.4 mm，遠小于末端執行器200 mm的開度，滿足該機器人末端執行器的采摘工作要求，驗證了通過文中所提出的方法建立混聯采摘機器人運動學正解方程的可行性及方程的正確性。該研究可為后續開展混聯采摘機器人控制方法和軌跡規劃研究提供參考。

機器人；運動學；模型；旋量理論；機械臂；混聯機器人

0 引言

近年來隨著中國油茶種植產業的快速發展，油茶果采摘機械化程度低、人工采摘油茶果效率低下的問題日益凸顯，因此研制能夠提高生產效率、降低勞動強度的油茶果自動化采收裝備成為中國未來油茶產業發展的基本趨勢。因此本項目組針對油茶果、果樹的生長特性，研究開發了一種油茶果混聯采摘機器人。根據給定的各關節轉角或位移，確定機器人末端執行器位置和姿態的機器人正運動學，是進一步開展機器人研究的基礎，對于機器人工作空間分析，軌跡規劃，運動控制及誤差補償等方面具有極重要作用。

對機器人開展正運動學研究的傳統方法是Denavit-Hartenberg(D-H)參數法[1]，但該方法需要為每個關節建立局部坐標系，各坐標系的姿態根據關節類型的不同而有所區別，并且在改變機器人構型后，需要重新建立坐標系，建模過程復雜繁瑣，幾何意義不明顯[2-6]。而利用基于旋量理論的指數積公式（product of exponential，POE）進行正運動分析時只需要建立基礎坐標系S和末端工具坐標系T，坐標系建立過程簡單易懂，充分了利用機器人的幾何特性，使得指數積公式（旋量法）成為D-H參數法的最佳替代[7]。

目前國內外學者對旋量法在串、并聯機器人領域的應用做了大量研究，并獲得了一批研究成果[8-13]。Jaime 等[14]采用基于旋量理論的指數積運動學建模方法對Delta機器人進行了正運動學分析，求解了動平臺速度、加速度輸入輸出方程，有利于后續根據并聯機構運動性能指標進行參數設計；Kong等[15]基于螺旋理論，提出了一種對三自由度移動機構進行分析的方法，并對該類機構主動關節的有效性條件進行了分析；陳偉海等[16]基于旋量理論對一種模塊化冗余度機器人進行了運動學分析，簡化了具有任意自由度和任意構型的模塊化機器人的運動學建模過程；莊未等[17]建立了基于螺旋理論的四足機器人運動學模型，給出了單腿串聯和軀體并聯運動學方程，并通過仿真驗證了模型的正確性；張付祥等[18]利用旋量理論對一種閉鏈級聯式機器人進行了正運動學分析，并在此基礎上提出了一種基于旋量理論建立閉鏈級聯式機器人運動學方程的方法。作為本文研究對象的混聯采摘機器人是在并聯機器人運動臺上擴展串聯結構得到的，其運動學分析方法與單一的串聯或并聯機器人有所不同，而由上面可知，旋量理論在混聯機器人運動學領域的研究和應用還不多，也未歸納出具有通用性的方法。

本文介紹了一種2P4R6自由度油茶果混聯采摘機器人，并以該機器人為研究對象，分析其機械結構，提出一種利用旋量理論開展混聯機器人運動學研究的一般性方法，利用該方法構建機器人運動學模型，通過試驗驗證基于旋量理論構建混聯機器人運動學模型的可行性及該模型的正確性，以期為后續研究混聯機器人控制方法和軌跡規劃提供參考。

1 基于旋量理論的運動學模型

1.1 旋量理論基礎

剛體從一個位置到另一個位置的運動可以通過繞某直線的轉動加上沿平行于該直線的移動得到，這種轉動與移動的組合稱為旋量運動[7]。

若設與剛體固連的動坐標系為B，慣性坐標系為A，那么剛體在A上的位姿變換集合可表示為

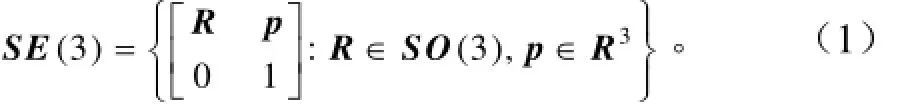
式中SE(3)為三維空間中剛體變換集合的特殊歐式群；R ∈SO(3)為B系相對于A系的姿態矩陣；p∈R3為B系相對于A系的位置矢量；SO(3)是一個以單位矩陣I作為單位元素的群；R3是以3維列向量作為單位元素的群。

若剛體以單位速度繞ω=(ωx，ωy，ωz)T∈R3旋轉軸純轉動θ角度，則剛體從初始位置到最終位置坐標之間的變換可以用矩陣指數表示為

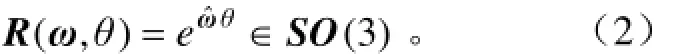
通常采用下面的Rodriguez公式計算矩陣指數

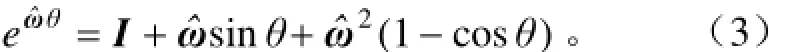
式中I為3×3的單位矩陣。

當剛體繞ω=(ωx，ωy，ωz)T∈R3旋轉軸做旋量運動時，如圖1所示，由Chasles定理[7]知，可由既繞ω=(ωx，ωy，ωz)T∈R3旋轉軸轉動θ角又沿平行于ω軸方向直線平移v的復合運動來實現，則相應的剛體位姿變換g用矩陣指數表示為

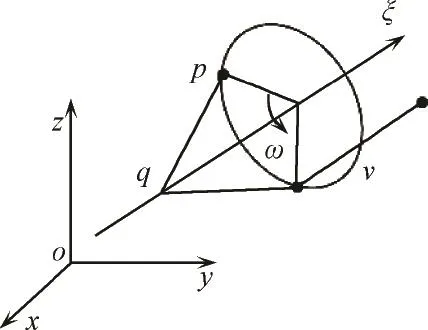
圖1 剛體的旋量運動Fig.1 Rotation of rigid body

根據式（3），可以將式（4）展開成下面的形式

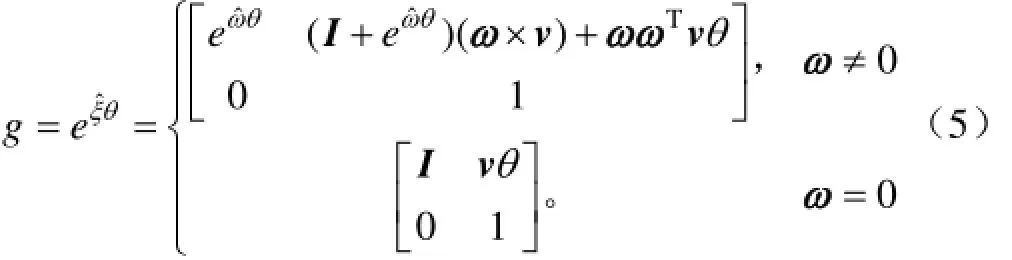
如上所述，運動旋量的指數可以表示剛體的相對運動，即剛體上經過旋量運動后，與剛體固連的B系相對于固定的A系的瞬時位姿變換為

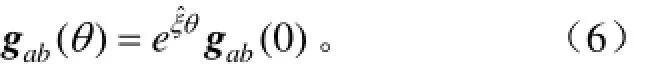
式中gab(0)為初始位姿時B系與A系之間的剛體位姿換；gab(θ)為B系相對A系的最終位姿變換。

1.2 指數積方程

對于n自由度的開鏈機器人，末端執行器位姿是由各關節復合運動構成的。當給定一組關節轉角，希望確定末端工具坐標系T相對于基礎坐標系S的位形。對于第i（i=1, 2, …, n）個關節可以構造一個運動旋量，對應于除該關節以外其他關節均固定于零位時的旋量運動。對于轉動關節，運動旋量的坐標表示形式為

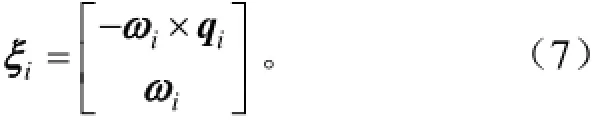
對于移動關節，運動旋量?iξ的坐標表示形式為

式中ωi∈R3為第i個關節軸線上的單位矢量；qi∈R3為第i個關節軸線上的任意一點坐標；vi為第i個關節移動方向上的單位矢量；ξi為運動旋量?iξ的坐標表示形式。

將各關節運動加以組合，即得到機器人運動學正解的指數積方程

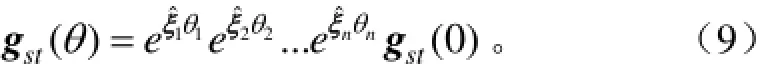
式中gst(θ)為T系相對S系的最終位姿；gst(0)為初始位形時T系與S系之間的剛體位姿變換；為第n個關節的運動旋量；θn為第n個關節的轉動量；為θn的矩陣指數。

2 混聯采摘機器人機械臂結構分析

圖2為2P4R6自由度混聯采摘機器人機械臂的三維模型。該機器人主要由腰部、手臂、腕部組成。腰部基座1為整個機器人的基礎部分，與手臂結構通過旋轉關節連接，可驅動除腰部以外的其余部分繞腰部關節旋轉；手臂部分主要包括旋轉座2、前臂4、后臂7、后小臂8、下小臂10、上小臂11、三角形連接件9，旋轉座為整個手臂提供支撐，上面安裝有水平滑塊3和豎直滑塊6，其中水平滑塊與前臂下端通過鉸鏈連接，豎直滑塊與后臂下端通過鉸鏈連接，下小臂和上小臂的末端與腕部基座12鉸接；腕部則由3個串聯的旋轉關節組成。

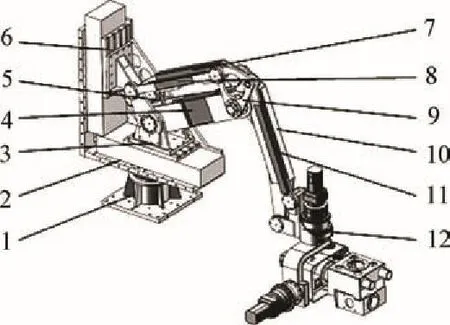
圖2 混聯采摘機器人機械臂參數化三維模型Fig.2 Parameterized manipulator model of hybrid harvesting robot

手臂結構中前臂和后臂下端通過主臂連桿5連接，前臂與后臂相互平行，主臂連桿與下小臂相互平行，四者構成一個平行四邊形機構，不僅增加了手臂結構部分的剛度，而且可以通過較小的驅動行程獲得末端執行器較大的工作行程，從而滿足了采摘作業對機器人工作空間的性能要求。機器人通過控制腰部和腕部關節的轉動實現末端執行器姿態調整，通過控制腰部旋轉、手臂的關節移動實現對末端執行器的位置調整，這樣設計使得機器人腕部減少了2個自由度，減輕了手臂末端運動負荷，使機器人在保證同樣自由度的情況下，讓驅動電機靠近基座，減少末端執行器產生的高頻振動對驅動電機及關節的不利影響，適合于振動采摘機器人的作業環境。

3 機械臂正運動學分析

3.1 基于旋量理論的混聯機器人的運動學分析方法

由于混聯機器人通常都是在并聯機器人運動臺上擴展串聯結構得到的，因此總是能從混聯機器人中找到一條主運動鏈，這條主運動鏈可以看成一個串聯機器人，主運動鏈中的部分構件又從屬于并聯機器人，可以把混聯機器人看成是由并聯機器人驅動關節運動的串聯機器人。針對混聯機器人的這一特點，綜合旋量理論進行串、并聯機器人運動學分析的方法，提出基于旋量理論的混聯機器人運動學方程構建方法：首先確定混聯機器人主運動鏈和副運動鏈，構建兩條運動鏈在參考位形時的結構方程等式，通過化簡等式獲得主運動鏈中被動關節與主、副運動鏈中主動關節的位姿映射關系；然后運用指數積公式對主運動鏈進行分析，得到主動鏈各關節與末端執行器的位姿映射關系，此時該位姿映射關系包含了被動關節參數；最后綜合上面所求得的2種位姿映射關系式，即得到機器人主動關節與末端執行器只包含有主動關節參數的位姿映射關系，完成混聯機器人的運動分析。

3.2 確定主運動鏈關節與主動關節映射關系

圖3為機械臂結構簡圖及參考位形，從腰部旋轉座到腕部基座bFF′的構件組成了機械臂的手臂（并聯結構部分），腰部旋轉座為該并聯結構的旋轉座、腕部基座bFF′為動平臺[19]，豎直滑塊、后臂lAD、下小臂lDF和水平滑塊、后小臂lC′E″、三角形連接件bEE′E″、上小臂lE′F′分別組成了并聯結構的2條串聯運動鏈。本文中選擇垂直導軌滑塊所在的運動鏈為主運動鏈，水平導軌滑塊所在的運動鏈為副運動鏈。

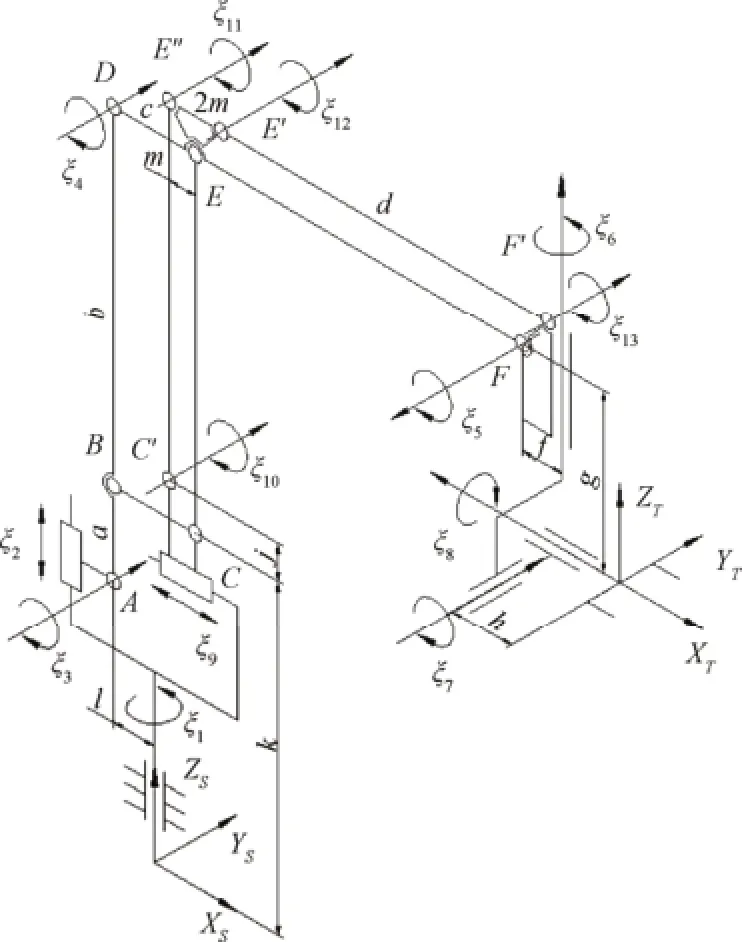
圖3 機械臂結構簡圖及參考位形Fig.3 Structure diagram and reference position of manipulator

圖3所示的機器人位形為θi=0時的參考位形，一般位形的結構方程為

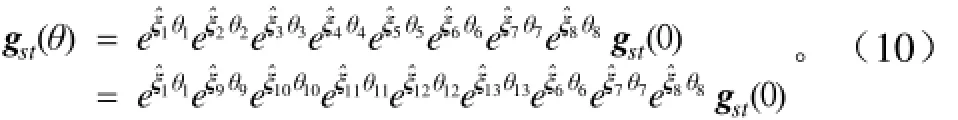
整理式（10），可得

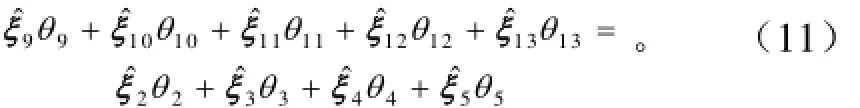
由圖3可知各關節軸單位矢量為

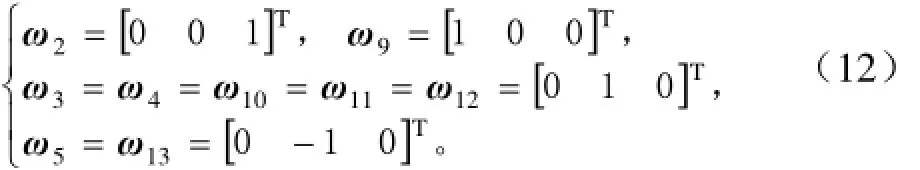
根據機器人結構參數取各軸線上的點為

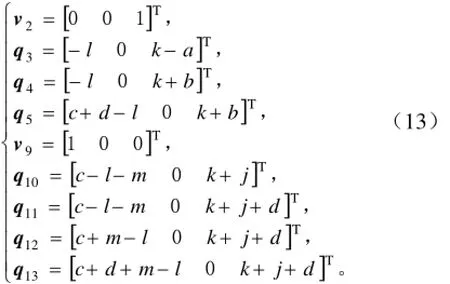
式中a為圖3中A、B之間的距離，mm；其余同理。

由式（8）可求解機器人水平滑塊、豎直滑塊的運動旋量坐標，由式（7）可求得其余關節的運動旋量坐標。

前面對機器人結構分析可知，水平滑塊和豎直滑塊為機械臂中并聯結構中的主動件，即β=[θ2，θ9]T為主動關節，α=[θ3，θ4，θ5，θ10，θ11，θ12，θ13]T為被動關節，則可將并聯部分的結構方程（11）調整為

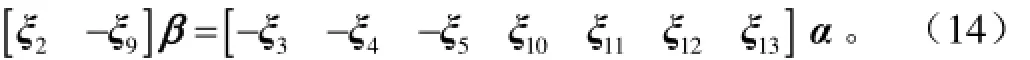
當給定主動關節位置β時，即可解出α。那么被動關節旋轉角度θ3、θ5與主動關節之間的映射關系為

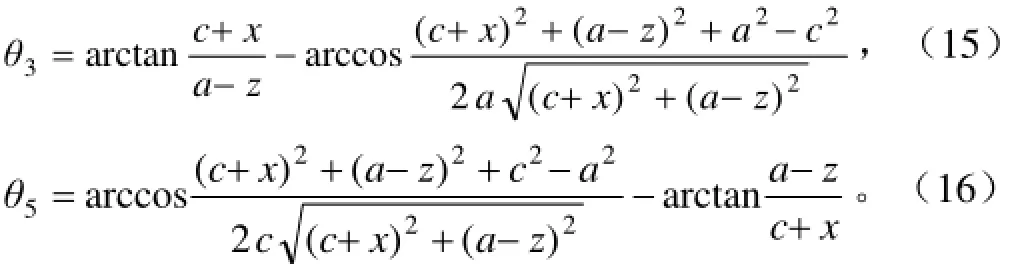
式中x為水平滑塊的位移量，在圖3中所對應的運動旋量坐標為ξ9，mm；z為豎直滑塊的位移量，在圖3中所對應的運動旋量坐標為ξ2，mm。

3.3 建立主運動鏈運動學正解方程

當θi=0時T系與S系的初始位姿變換為

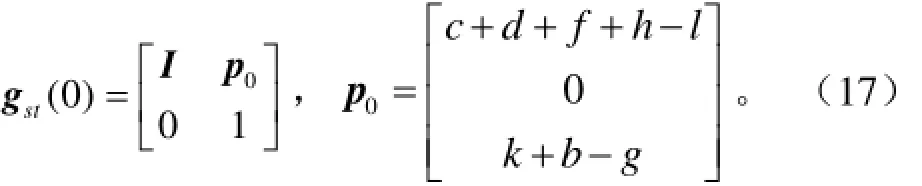
式中f為圖3中鉸接點F與運動旋量ξ6之間的距離，mm；其余同理。

由圖3可知主動鏈中未求解的各關節軸單位矢量為

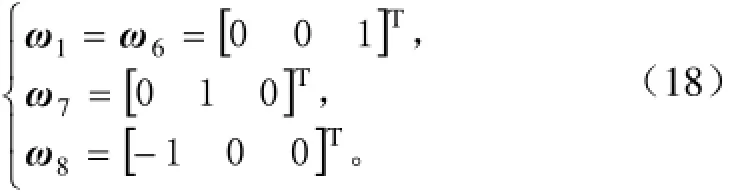
根據機器人結構參數取各軸線上的點為

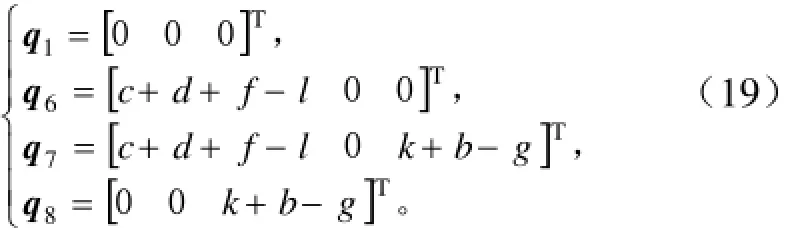
由式（9）可求得主動鏈中尚未求解的各關節運動旋量坐標。由于選擇垂直滑塊所在的運動鏈為主動鏈，則主運動鏈運動學正解方程為

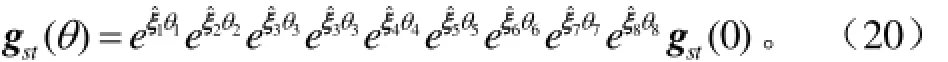
展開可得

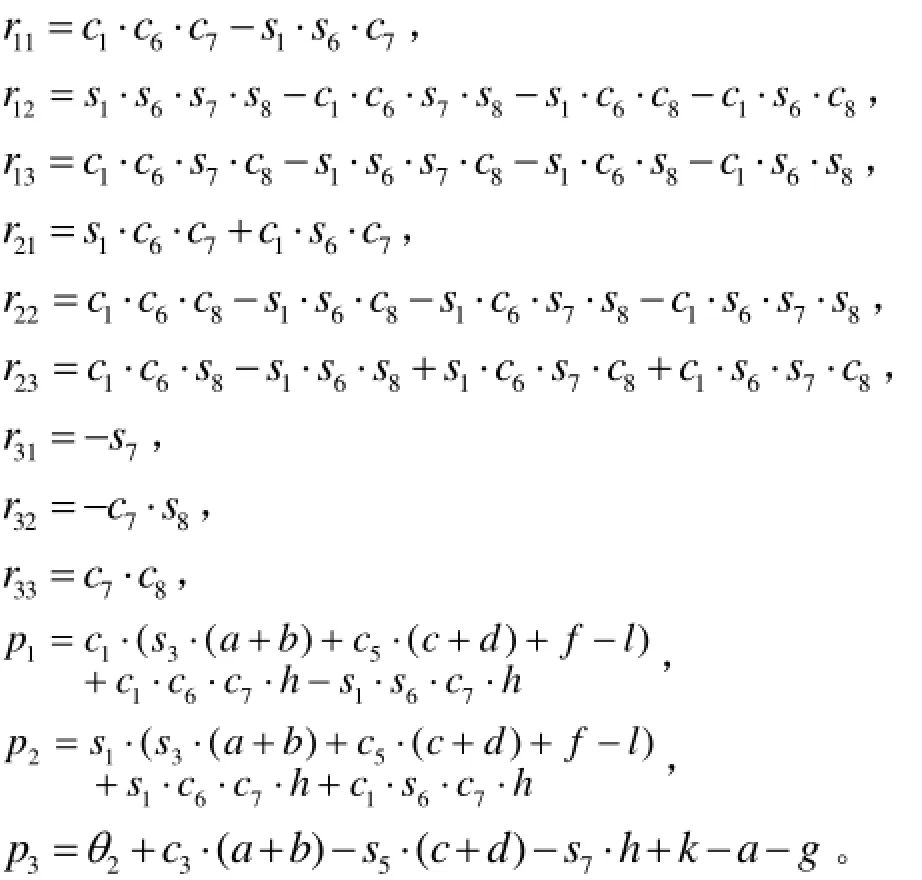
其中ci=cosθi，si=sinθi。

3.4 機械臂末端執行器運動學正解方程

機器人運動學正解方程只包含有主動關節參數，而上面p(θ)包含了被動關節參數θ3、θ5。為消去主運動鏈運動學正解方程中的被動關節參數，將主運動鏈關節與主動關節映射關系式（15）、式（16）代入到p(θ)中，得到消去了被動關節參數θ3、θ5的pe(θ)。獲得了混聯采摘機器人機械臂運動學正解方程（18）。對p(θ)求關于時間的一階導后整理即可得到機械臂速度正解方程，求二階導整理可得到機械臂加速度正解方程。

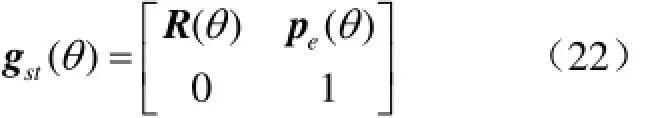
式中pe(θ)=[pe1pe2pe3]T為只包含有主動關節參數的機器人末端執行器位置矢量。

4 運動學試驗與分析

為驗證本文所提出的算法及基于該算法所構建的機器人運動學正解方程的正確性，利用采摘機器人實體樣機所搭建的運動學試驗平臺進行了運動學試驗[20-21]。圖4為運動學試驗平臺，該平臺左側為三維坐標測量儀，右側為采摘機器人。采摘機器人以腰部旋轉基座的中心軸線為基礎坐標系S的Z軸，以機器人腰部旋轉基座的底面為XOY平面。測量儀基礎坐標系S′在采摘機器人基礎坐標系S中的位置坐標為（1 500，0，0），其各坐標軸方向與S系一致。試驗過程中，通過三維坐標測量儀直接測得采摘機械臂末端執行器上的標記點相對測量儀基礎坐標系S′的坐標，然后通過簡單換算求得末端執行器標記點在機器人基礎坐標系中的位置坐標。

圖4 運動學試驗平臺Fig.4 Test platform of kinematics

設定ω1=-5t，ω6=10t，ω7=-10t，ω8=-10t，νx=15t，νz=20t，其中ωi為第i個關節的角速度，rad/s；νx為水平滑塊速度，mm/s；νz為豎直滑塊移動速度，mm/s；t為時間變量，s。選取1、2、3、4、5 s時的5組關節變量值，并將這5組數值和表1中的機械臂結構參數代入到機械臂運動學正解方程（22）中，利用Matlab軟件編寫程序計算得出機械臂末端執行器的理論位置坐標值，然后將5組關節變量值輸入至機械臂控制軟件中，控制機械臂各個關節運動，使機械臂末端執行器達到各組關節變量所對應的最終位置，通過三維坐標儀測量獲得機械臂末端執行器的實際位置坐標值。

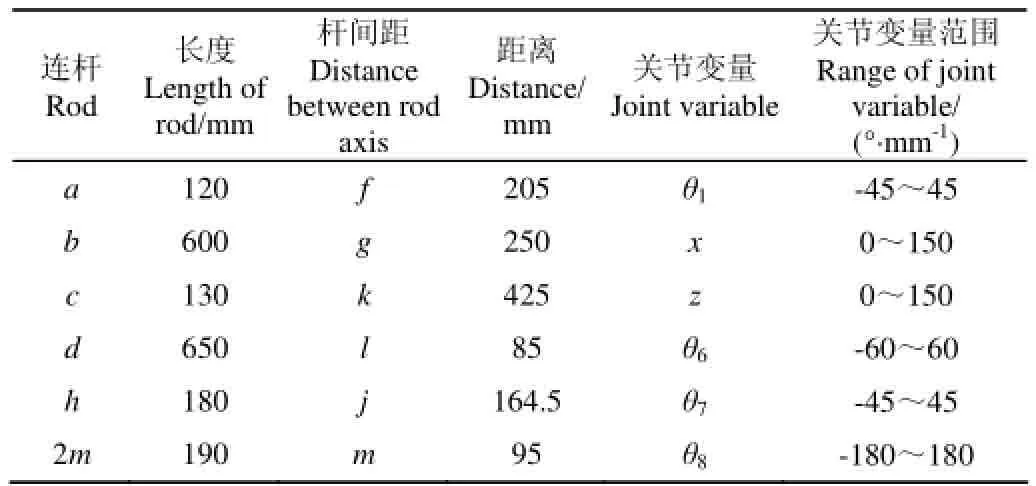
表1 機械臂結構參數Table 1 Structure parameters of manipulator

根據試驗結果整理可以得到表2所示的機器人末端執行器在X、Y、Z軸上的位置誤差。由表2可知，末端執行器在X、Y、Z軸上的最大絕對位置誤差為10.4 mm，可以通過提高機器人幾何參數和關節伺服定位的精度來降低該誤差。本文所提出的油茶果混聯采摘機器人是以油茶果樹干作為目標夾持對象，其10.4 mm的末端執行器最大絕對位置誤差遠小于200 mm的最大開度，滿足該機器人末端執行器夾持樹干的作業要求，證明了本文所提出的基于旋量理論的混聯機器人運動學分析方法的可行性和正確性。

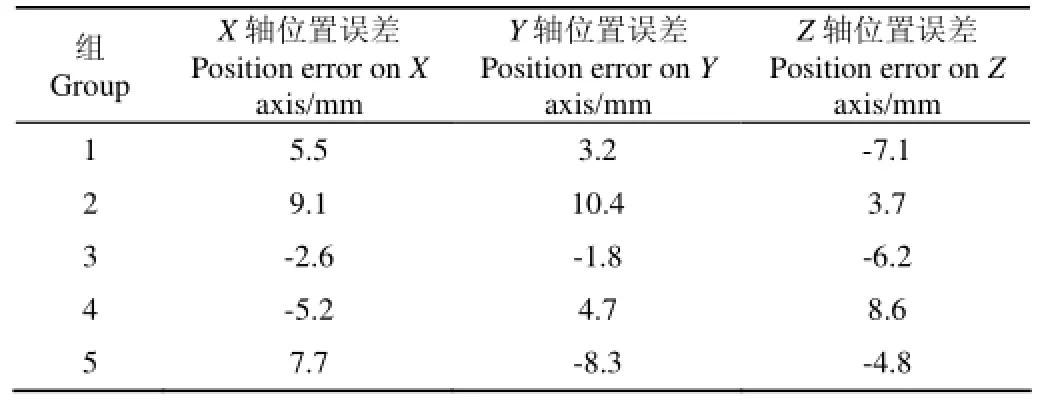
表2 末端執行器位置誤差Table 2 Position error of end effector

5 討論

本文針對利用D-H參數法在建立混聯采摘機器人正運動學方程時過于復雜的問題，提出了一種基于旋量理論構建混聯機器人運動學正解方程的一般性方法。但機器人實際采摘過程中，往往是先由視覺系統對目標樹干進行定位檢測后，利用該目標樹干位姿信息推導期望的機器人末端執行器位姿，再反向求解對應的各個關節轉角或位移，這種通過末端位姿反向求解各關節的過程稱為逆運動學分析。為發揮旋量理論在進行機器人運動學分析的優勢以及為機器人系統的運動規劃等問題的研究提供基礎,后續擬基于旋量理論對該混聯采摘機器人進行逆運動學分析。

本文中所進行的試驗是在實驗室無枝葉、果實遮擋的理想環境中完成的。實際的采摘過程中，末端執行器為避讓枝葉、果實，順利夾取樹干，不僅要滿足位置要求，還需滿足姿態要求。試驗得到的機器人末端執行器的位置絕對誤差最大為10.4 mm，雖然滿足機器人末端執行器對于夾取樹干的要求，但是誤差絕對值較大，會造成對機器人其他系統（如視覺識別系統）提出較高的精度要求。因此為提高末端執行器位姿精度，降低對機器人其他系統的精度要求，項目組后續擬開展該機器人樣機位姿誤差分析以及機器人位姿誤差補償等研究工作。

6 結論

1）本文中所提出的油茶果混聯采摘機器人采用平行四邊形構型作為手臂結構，不僅可增加整個手臂的剛度，而且可以通過較小的驅動行程獲得末端執行器較大的工作行程，從而滿足了振動采摘作業對機器人結構強度以及末端執行器較大工作空間的性能要求。

2）本文提出了基于旋量理論構建混聯機器人運動學正解方程的方法，該方法首先對混聯機器人運動鏈進行分解，由此將混聯機器人正運動學問題轉化成單開鏈機器人以及單開鏈中被動關節與機器人主動關節映射關系的運動學子問題，然后利用指數積公式和結構方程等數學工具求解上述子問題，最后綜合各子問題結果就獲得了混聯機器人的運動學正解方程。

3）本文對混聯采摘機器人進行了結構分析，利用所提出的運動學分析方法，建立了該機器人機械臂運動學正解方程。利用該方程和機器人運動學試驗平臺分析得到末端工具坐標系位置理論值和實際值之間最大絕對誤差為10.4 mm，遠小于末端執行器200 mm的開度，滿足末端執行器的夾持要求。由此驗證了本文所提出方法對構建混聯采摘機器人運動學正解方程的可行性及正確性。

[1] Santolaria J, Juan-José A, José-Antonio Y, et al. Kinematic parameter estimation technique for calibration and repeatability improvement of articulated arm coordinate measuring machines[J]. Precision Engineering, 2008, 32(4): 251－268.

[2] 張志強. 混聯碼垛機器人運動學分析及仿真[J]. 機械設計，2010，27(11)：47－51. Zhang Zhiqiang. Kinematics analysis and simulation of series-parallel palletizing robot[J]. Journal of Machine Design, 2010, 27(11): 47－51. (in Chinese with English abstract)

[3] 孫祥溪. 工業碼垛機器人運動學仿真[J]. 計算機仿真，2013，30(3)：303－306. Sun Xiangxi. Kinematics simulation of industrial palletizing robot[J]. Computer Simulation, 2013, 30(3): 303－306. (in Chinese with English abstract)

[4] 張翔. 基于D－H法油茶果采摘機器人正運動學分析[J].農機化研究，2014，4(4)：25－28. Zhang Xiang. Forward kinematics analysis of the camellia oleifera picked robot based on the D-H method[J]. Journal of Agricultural Mechanization Research, 2014, 4(4): 25－28. (in Chinese with English abstract)

[5] 張金玲. 新型可控碼垛機器人機構運動學與動力學研究[D].南寧：廣西大學，2013. Zhang Jinling. Research on Kinematic and Dynamic of a Novel Palletizing Robot with Controllable Mechanism[D]. Nanning: Guangxi University, 2013. (in Chinese with English abstract)

[6] 劉揚. 混聯碼垛機器人運動學分析與仿真[J]. 機械與電子，2010，3：57－60. Liu Yang. Kinematics analysis and simulation of the hybrid stacking robot[J]. Machinery & Electronics, 2010, 3: 57－60. (in Chinese with English abstract)

[7] 理查德·摩雷，李澤湘，夏恩卡·薩思特里．機器人操作的數學導論[M]. 徐衛良，錢瑞明，譯. 北京：機械工業出版社，1998：11－80.

[8] 盧宏琴. 基于旋量理論的機器人運動學和動力學研究及其應用[D]. 南京：南京航空航天大學，2007. Lu Hongqin. Kinematics and Dynamics Research of Robot Manipulators and Its Application Based on Screw Theory[D]. Nanjing: Nanjing University of Aeronautics and Astronautics, 2007. (in Chinese with English abstract)

[9] 王小榮. 仿人機器人基于旋量理論的運動學分析方法[J].蘭州交通大學學報，2010，29(1)：73－75. Wang Xiaorong. Screw theory based method of kinematic analysis on humanoid[J]. Journal of Lanzhou Jiaotong University, 2010, 29(1): 73－75. (in Chinese with English abstract)

[10] 田海波. 串聯機器人機械臂工作空間與結構參數研究[J].農業機械學報，2013，44(4)：196－201. Tian Haibo. Workspace and structural parameters analysis for manipulator of serial robot[J]. Transactions of the Chinese Society for Agricultural Machinery, 2013, 44(4): 196－201. (in Chinese with English abstract)

[11] 朱大昌. 基于螺旋理論的3-RPS型并聯機器人運動學分析[J].機械設計與制造，2011，7：149－150. Zhu Dachang. Kinematic analysis of 3-RPS type parallel robot based on screw theory[J]. Machinery Design & Manufacture, 2011, 7: 149－150. (in Chinese with English abstract)

[12] 宮金良，黃風安，張彥斐. 基于指數積的Delta機器人運動學正解建模[J]. 北京理工大學學報，2013，33(6)：581－585. Gong Jinliang, Huang Feng’an, Zhang Yanfei. Direct kinematic analysis of delta robot based on exponential product[J]. Transactions of Beijing Institute of Technology, 2013, 33(6): 581－585. (in Chinese with English abstract)

[13] 張云嬌. 基于旋量理論的3-US并聯機構運動學[J]. 機械設計與研究，2014，30(2)：8－11. Zhang Yunjiao. Kinematic analysis of a 3-US parallel mechanism using screw theory[J]. Machine Design and Research, 2014, 30(2): 8－11. (in Chinese with English abstract)

[14] Jaime G. An application of screw theory to the kinematic analysis of a delta-type robot[J]. Journal of Mechanical Science and Technology, 2014, 28(9): 3785－3792.

[15] Kong X W, Lin C M. Type synthesis of 3-dof translational parallel manipulators based on screw theory[J]. Journal of Mechanical Design, 2004, 126(1): 83－92.

[16] 陳偉海. 基于螺旋理論模塊化機器人運動學分析與仿真[J].北京航空航天大學學報，2005，31(7)：814－818. Chen Weihai. Kinematic analysis and simulation for modular manipulators based on screw theory[J]. Journal of Beijing University of Aeronautics and Astronautics, 2005, 31(7): 814－818. (in Chinese with English abstract)

[17] 莊未. 基于螺旋理論的冗余液壓驅動四足機器人運動學分析[J]. 機械設計，2011，28(11)：15－21. Zhuang Wei. Kinematic analysis of redundant hydraulic actuated quadruped robot based on screw theory[J]. Journal of Machine Design, 2011, 28(11): 15－21. (in Chinese with English abstract)

[18] 張付祥. 閉鏈級聯式機器人基于旋量理論的運動學分析方法[J]. 機械工程學報，2006，42(4)：112－117. Zhang Fuxiang. Screw theory based method of kinematic analysis on tandem robots of closed chains[J]. Chinese Journal of Mechanical Engineering, 2006, 42(4): 112－117. (in Chinese with English abstract)

[19] 黃真. 并聯機器人機構學理論及控制[M]. 機械工業出版社，1997.

[20] 權龍哲. 三臂多功能棚室農業機器人的運動學分析及試驗[J].農業工程學報，2015，31(13)：32－38. Quan Longzhe. Kinematics analysis and experiment of multifunctional agricultural robot in greenhouse with three arms[J]. Transactions of the Chinese Society of Agricultural Engineering (Transactions of the CSAE), 2015, 31(13): 32－38. (in Chinese with English abstract)

[21] 肖名濤. 雙平行多桿栽植機構運動學分析與試驗[J]. 農業工程學報，2014，30(17)：25－33. Xiao Mingtao. Kinematic analysis and experiment of dual parallelogram multi-pole planting mechanism[J]. Transactions of the Chinese Society of Agricultural Engineering (Transactions of the CSAE), 2014, 30(17): 25－33. (in Chinese with English abstract)

Forward kinematics analysis and experiment of hybrid harvesting robot based on screw theory

Yang Hanjiang, Li Lijun※, Gao Zicheng
(School of Mechanical and Electrical Engineer, Central South University of Forestry and Technology, Changsha 410000, China)

In this paper, the research progress of the camellia oleifera fruit harvesting equipment was introduced. This paper simplified the structure of the 2P4R hybrid camellia oleifera fruit harvesting robot, which included waist part, arm part and wrist part. The manipulator could accomplish 6 kinds of movements including waist revolution, translational motion of vertical slider and horizontal slider, and 3 kinds of revolute motions of the wrist part. In arm part, the fore-arm is linked with back-arm by 2 components; one is link-bar below and the other is lower-arm above. Fore-arm is paralleled with back-arm and link-bar is paralleled with lower-arm. It means these 4 components form a parallel quadrilateral mechanism, which not only increases the stiffness of the arm part, but also can obtain larger end effector working space through a smaller drive stroke, and thus, the harvesting robot meets the requirements of large end effector working space when it clamps the camellia oleifera trunk. Robot can adjust the posture and position of the end effector by controlling the rotation of waist part and wrist part and the translation of arm part respectively. It makes the wrist part decrease by 2 degrees of freedom, lightens the burden of the arm, and also reduces the adverse effect of high-frequency vibration when the robot harvests camellia oleifera fruit. The screw theory and a kind of kinematics analysis method for hybrid robot were introduced. With the proposed method, firstly, the open chain from the waist part to the end effector of the manipulator was defined, which contained the vertical slider as major chain, and the kinematic analysis problem of hybrid robot was turned to the sub-problems of the kinematic analysis of an open major chain and a single closed chain; secondly, the kinematics equation of the closed chain and major chain was established, and then the conversion formula between the driving joint variable in closed chain and the passive joint variable in major chain was obtained by figuring out the equation of the closed chain; thirdly, the position of the end effector was got from the kinematics analysis of the closed chain by using the Lie group, Lie algebra, screw theory and product-of-exponential formula; and finally the positive kinematics equation for the position of the end effector was obtained from the synthesized results of the kinematic analysis of the major chain and closed chain. The first-order and second-order derivative of the position equation were the velocity equation and acceleration equation of the manipulator respectively. In order to verify the feasibility of the proposed method and the correctness of the kinematics equation, select a group of joint variable values, and then figure out the theoretical position coordinate of the end effector by putting the values into the kinematical equation in Matlab. A test platform for kinematics experiment was built, which consists of a three-dimensional position measuring instrument and a camellia oleifera fruit hybrid harvesting robot. The three-dimensional position measuring instrument was used to measure the actual position coordinates of the end effector directly, which was driven by the selected values. From the comparison between the theoretical and actual results, it was found that the maximum position error between kinematical equation resolution and actual position coordinate of the end effector was 10.4 mm, which was significantly smaller than 200 mm, the open size of the end effector. From the above experiment results, the correctness of the kinematics equation of the manipulator based on the proposed method was verified. Therefore, the application of the proposed method based on screw theory in kinematics analysis is beneficial for establishing the control method and trajectory planning.

robots; kinematics; models; screw theory; manipulator; hybrid robot

10.11975/j.issn.1002-6819.2016.09.008

TP24

A

1002-6819(2016)-09-0053-07

陽涵疆，李立君，高自成. 基于旋量理論的混聯采摘機器人正運動學分析與試驗[J]. 農業工程學報，2016，32(9)：53－59.

10.11975/j.issn.1002-6819.2016.09.008 http://www.tcsae.org

Yang Hanjiang, Li Lijun, Gao Zicheng. Forward kinematics analysis and experiment of hybrid harvesting robot based on screw theory[J]. Transactions of the Chinese Society of Agricultural Engineering (Transactions of the CSAE), 2016, 32(9): 53－59. (in Chinese with English abstract) doi：10.11975/j.issn.1002-6819.2016.09.008 http://www.tcsae.org

2015-10-08

2016-02-26

國家林業公益性項目（201104090）；湖南省高校科技創新團隊支持計劃（2014207）

陽涵疆，男，湖南益陽人，主要從事機器人運動控制研究。長沙中南林業科技大學機電工程學院，410000。Email：yanghanjiang@hotmail.com※通信作者：李立君，女，湖南寧鄉人，教授，博士，主要從事現代林業裝備研究。長沙 中南林業科技大學機電工程學院，410000。

Email：junlili1122@163.com