基于增量式潛在語義分析的構件檢索算法

祝仰凱，高茂庭

（上海海事大學信息工程學院，上海　200000）

基于增量式潛在語義分析的構件檢索算法

祝仰凱，高茂庭

（上海海事大學信息工程學院，上海200000）

針對基于潛在語義分析的構件檢索算法，在應用與問題規(guī)模逐漸增大時，空間和時間復雜度也隨之提高的問題，提出一種增量式潛在語義分析的構件檢索算法，在進行增量矩陣的奇異值分解時，利用增量前矩陣的分解結果進行運算，從而避免重復運算。實驗結果表明，該算法能夠提高構件檢索效率。

潛在語義分析；增量式；構件檢索；向量空間模型

0　引言

軟件復用是在軟件開發(fā)中，避免重復勞動的解決方案，通過復用已有的高質量開發(fā)成果，避免重新開發(fā)可能引入的錯誤，可以降低開發(fā)費用、提高軟件開發(fā)的效率和質量。其中，軟件構件技術是實現(xiàn)軟件復用的重要環(huán)節(jié)，構件庫管理是其一項主要研究內容。構件庫管理中有兩個核心問題：構件分類和構件檢索，而且，對構件進行合理的分類可以提高構件的檢索效率。

每個構件在發(fā)布時，都會有該構件相應描述信息，根據(jù)這些描述信息，采用某種構件表示方法表示構件，這樣就會產(chǎn)生一個用來描述構件的文本。通過計算這些文本間的相似度就來得到構件之間的相似度，來實現(xiàn)軟件構件的檢索。

對文本的表示，Salton等人于20世紀70年代提出了向量空間模型（Vector Space Model，VSM），VSM把文本內容表示為多維空間的向量，計算文本的相似度就轉化為了計算兩個向量。但是基于向量空間模型的文本處理方法存在高維稀疏、同義詞和多義詞的問題。1988年S.T.Dumais等人提出潛在語義分析模型（Latent Semantic Analysis，LSA），把用向量空間模型表示的文本映射到低維潛在語義空間中，通過映射實現(xiàn)了對矩陣降維，同時去除原始向量空間中的一些“噪音”，凸顯文本的語義特征，這個映射通過對文檔-詞條矩陣進行奇異值分解（Singular Value Decomposition，SVD）來實現(xiàn)[1]。

使用潛在語義分析模型來處理構件文本，實現(xiàn)構件檢索，可以提高信息檢索精度。但是構件庫中的構件數(shù)量是不斷增多的，隨著構件庫規(guī)模逐漸增大，需要經(jīng)常性地進行奇異值分解，而奇異值分解的空間和時間復雜度較高，將導致構件的檢索效率不高。因此，本文提出增量式潛在語義分析的構件檢索算法，在進行增量矩陣的奇異值分解時，利用增量前矩陣的分解結果進行運算，減少計算量，提高檢索效率。

1　基本概念

1.1構件表示

目前構件檢索大部分都是基于刻面分類表示的，刻面具有靈活的多角度描述的特點，可以全面地描述構件。其中，刻面分類方法[2-3]以刻面的完整性和獨立性定義了4個刻面：

（1）構件類別：如系統(tǒng)工具、數(shù)據(jù)庫相關、用戶界面等；

（2）構件功能：構件功能描述，應用領域；

（3）運行環(huán)境：軟件環(huán)境和硬件環(huán)境；

（4）表示方法：構件形態(tài)（如類、構架、框架、模式）和開發(fā)語言。

采用構件文本來標識構件后，就可以用文本信息檢索的方法來實現(xiàn)檢索構件。在構件VSM模型中，每個構件文本被描述成由特征詞組成的特征向量，每個特征詞被視為特征空間中的一維。這樣，構件文本的相似度計算問題轉化為特征向量空間中的向量相似度計算問題，兩個文本間的相似程度可以用對應向量間的夾角余弦來度量，夾角越小，余弦值越大，說明文本間相似度越高，反之則相似度越低。VSM是基于特征詞之間關系相互獨立的假設，文本向量空間具有高維性和稀疏性的特點，而在文本中出現(xiàn)的詞通常存在一定的相關性，所以VSM也無法解決同義詞和多義詞的問題。

LSA是一種新的信息檢索代數(shù)模型[4]，解決了檢索中的同義詞、多義詞問題，減小了問題的規(guī)模，并且使得原本稀疏的數(shù)據(jù)不再稀疏。潛在語義分析中可以通過對文檔-詞條矩陣的奇異值分解（SVD）來實現(xiàn)的映射。

對一個文本集D=（d1，d2，…，dm）T，進行潛在語義分析的過程如下：

（1）將文本集D用一個m×n的文檔-詞條矩陣A [aij]，m>>n，1≤i≤m，1≤j≤n表示，其中，m表示文本個數(shù)，n表示文本集中所包含的詞條數(shù)，即列代表詞條向量，行代表文本向量；aij代表詞條在文本集中的權重；

（2）對文檔-詞條矩陣A進行奇異值分解（SVD），此時矩陣A可表示為3個矩陣的乘積：A=UΣVT；

（3）對奇異值分解后的矩陣進行降維，把矩陣Σ對角線上的值由大到小排列，保留Σ的前K個奇異值，得到ΣK，相應的保留U、V的前K個列向量，分別為UK、VK；

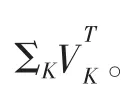
下面對LSA中用到的奇異值分解進行簡單介紹：

①奇異值的定義

定義設A∈Rm×n，且ATA的特征值為：

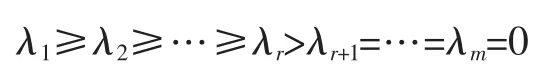
②奇異值分解定理

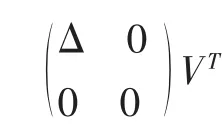
LSA利用了奇異值分解對文檔-詞條矩陣進行降維的方法處理文檔和詞條，然而奇異值分解的空間和時間復雜度較高，隨著問題規(guī)模逐漸增大，需經(jīng)常性地進行奇異值分解，將導致構件的檢索效率降低。

1.2構件相似度計算

用戶輸入一個查詢字符串q，要比較查詢字符串與已有文檔的相似性，需要把查詢字符串映射到語義空間，本文采用余弦相似度。計算過程如下：

（1）將查詢字符串以處理構件文本的同樣方式構造查詢向量，然后將其映射到語義空間：

（2）計算q*和dj的相似度：

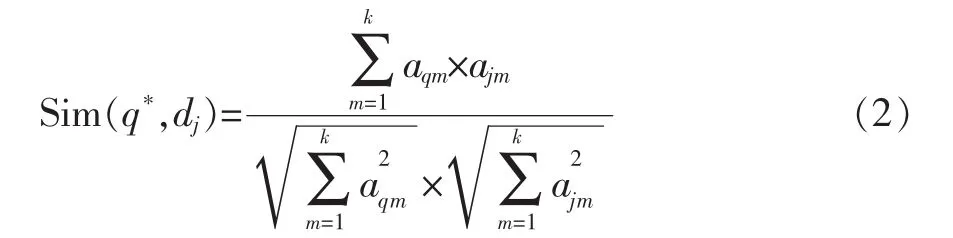
式（1）中，q*為查詢向量，dj為矩陣UK中的第j個文本向量，k為語義空間的維數(shù)，aqm、ajm分別為q*、dj中的第m維權值。

2　基于增量式潛在語義分析的構件檢索算法

潛在語義分析利用奇異值分解將文檔映射到低維的潛在語義空間中。由于奇異值分解的時間復雜度較高，隨著問題規(guī)模的逐漸增大，重新進行奇異值分解，會影響構件的檢索效率。因此，本文提出一種增量式潛在語義分析的構件檢索算法，在計算增量后矩陣的奇異值分解時，利用增量前矩陣的分解結果進行運算，從而避免重復運算，提高檢索效率。利用增量式奇異值分解的潛在語義分析我們稱之為增量式潛在語義分析算法。

2.1增量式奇異值分解

設矩陣A是m×n的矩陣，當矩陣A增加一行時，得到矩陣A'，此時需要計算矩陣A'的奇異值分解，若對矩陣A'重新進行SVD分解，則復雜度較高，為此，考慮利用已有的矩陣A的SVD分解結果。

文獻[5]中介紹了矩陣A增加一行以及增加一列之后的奇異值分解算法，對于大型構件庫而言，由于構件文本的個數(shù)遠大于詞條的個數(shù)，因此，本文只考慮矩陣A增加一行的情況。假定在矩陣A的最后增加一行，即

利用矩陣A的奇異值分解的結果，來計算A'的奇異值，計算過程如下：

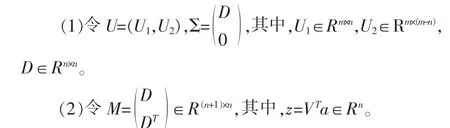
（3）利用1.2小節(jié)中的方法，對矩陣M進行奇異值分解：

（4）對矩陣A'進行奇異值分解：

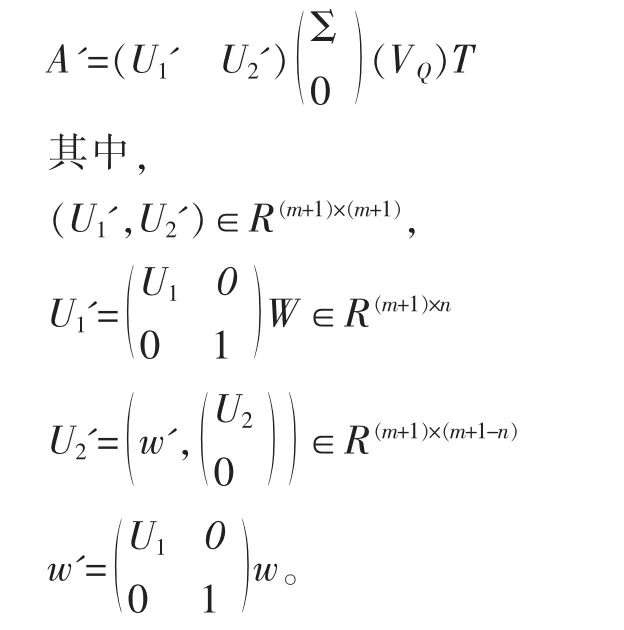
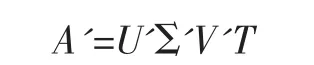
2.2矩陣M的奇異值分解

本文引用文獻[6]中計算矩陣M的奇異值分解的方法，通過計算矩陣的奇異值分解來近似的計算矩陣M的奇異值分解。

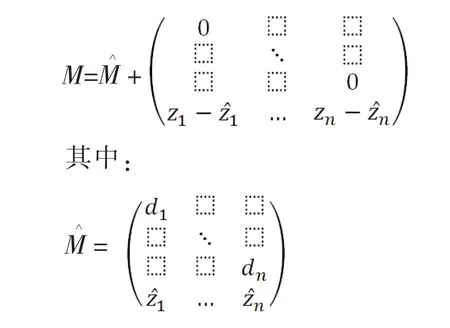
（1）計算矩陣M的奇異向量

公式（3）稱為久期函數(shù)[7]，通過求解它的根，計算出矩陣M的近似奇異值，然后利用公式（4）構建矩陣：

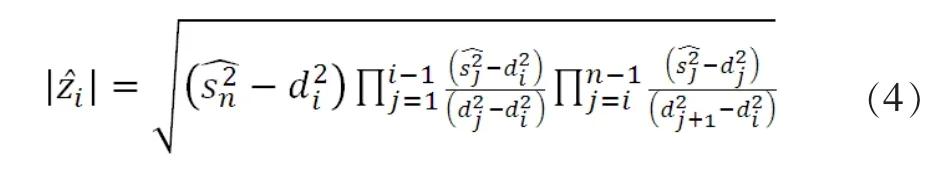
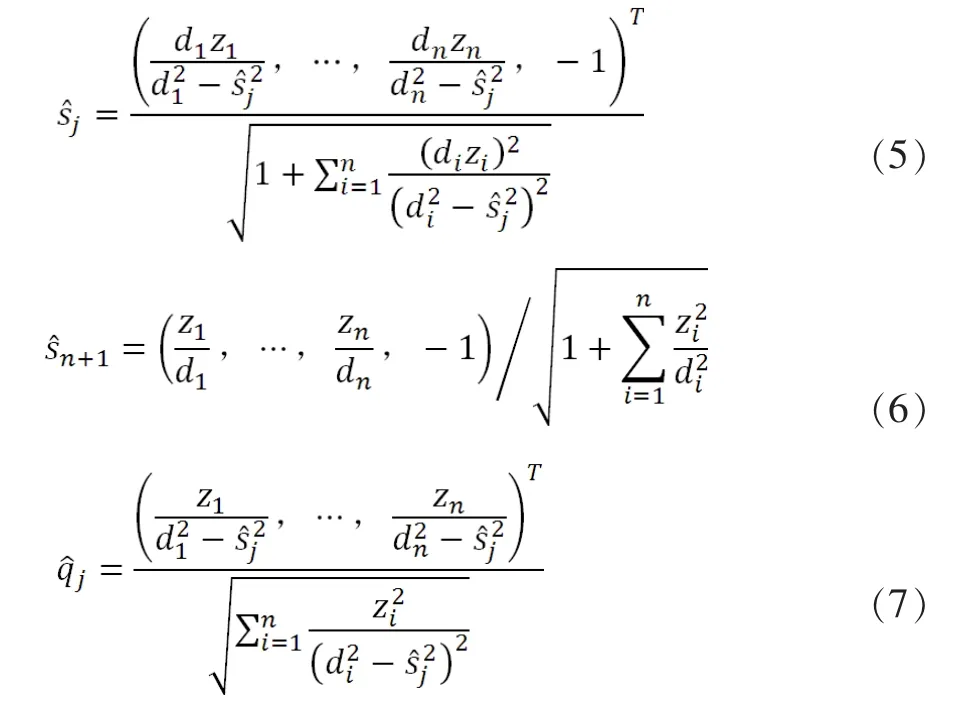
（2）計算矩陣M的奇異值

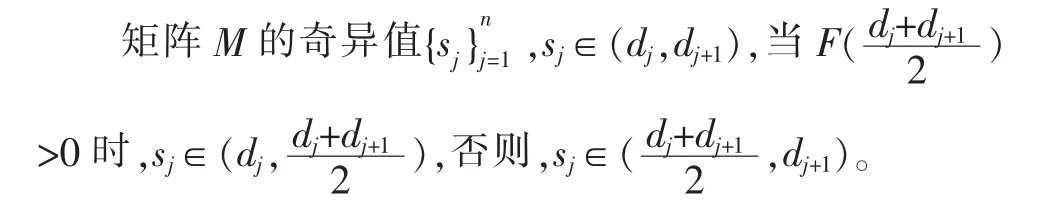
1）當1≤j≤n-1時，

通過計算方程組：

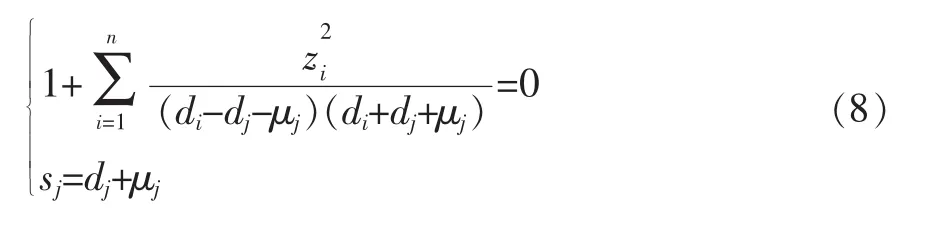
得到奇異值sj（1≤j≤n-1）。

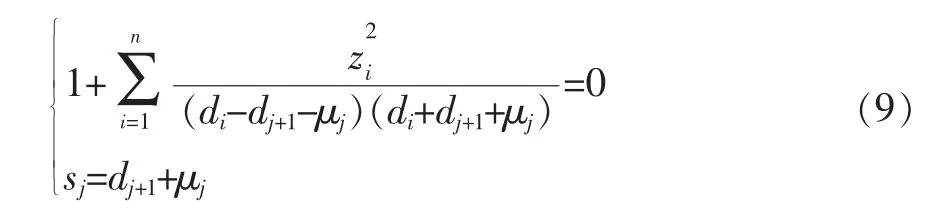
得到奇異值sj（1≤j≤n-1）。

2）當j=n時，通過計算方程組

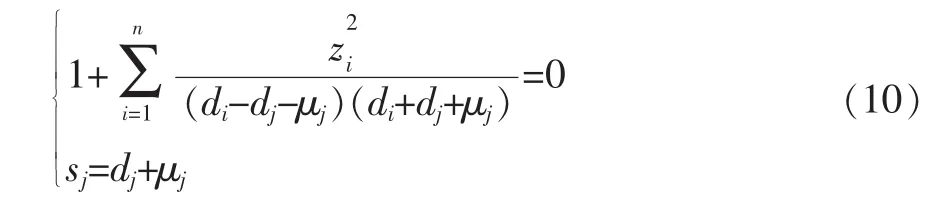
得到奇異值sn。

通過這種方法來計算矩陣M的奇異值分解的復雜度為O（n2）。

增量式潛在語義分析算法首先對文檔集進行中文分詞、權重計算生成文檔-詞匯矩陣，然后對該矩陣進行奇異值分解，并保留分解結果，當有新的文檔加入時，利用上次奇異值分解結果進行運算，構造潛在語義空間。增量式潛在語義分析算法的流程圖如圖1。

2.3基于增量式潛在語義分析的構件檢索算法

基于增量式潛在語義分析的構件檢索算法通過增量式奇異值分解算法，利用上一步分解結果來提高構件檢索的效率，其處理過程分為以下七步：

Step1采用刻面分類方法表示構件，使每個構件對應于一個文檔，從而形成一個構件文檔集，并將其作為輸入數(shù)據(jù)；

Step2利用增量式潛在語義分析算法處理構件文檔集，構造潛在語義空間；

Step3根據(jù)公式（1）對用戶輸入的查詢字符串建立提問式；

Step4根據(jù)公式（2）計算查詢字符串向量與構件間的相似度值Sim（q*，dj）；

Step5根據(jù)相似度由高到低對構件文檔進行排序，輸出結果。

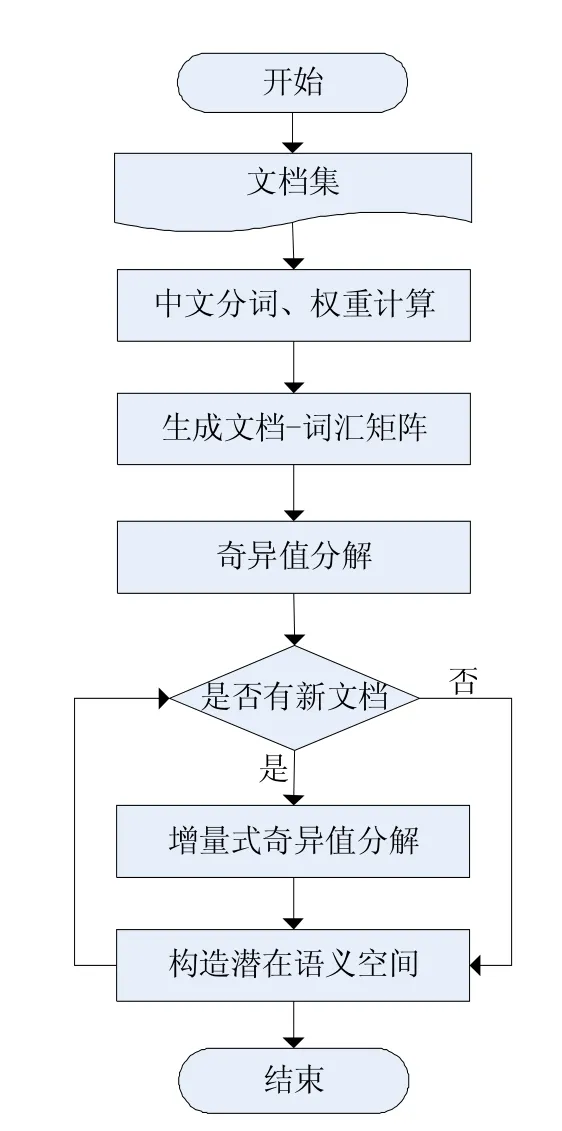
圖1　增量式潛在語義分析算法的流程圖

3　實驗結果及分析

為了驗證本文算法有效性，將本文提出的基于增量式潛在語義分析構件檢索算法與基于潛在語義分析構件檢索算法進行性能實驗對比。

實驗數(shù)據(jù)為從網(wǎng)上搜集構建的一個包含1500個構件的構件庫，包含三大主題：數(shù)據(jù)庫相關、用戶界面、系統(tǒng)工具。獲取構件庫中描述構件的文本集，利用Python進行文本分詞及關鍵詞提取，對于構件文本中關鍵詞權重的計算采用TF-IDF方法[4]。

3.1構件檢索性能評價指標

采用查準率，查全率以及算法的時間復雜度3個指標對本文算法進行評估。

查全率（R）：檢索系統(tǒng)在進行某一檢索時，檢索出正確匹配的構件文本數(shù)與系統(tǒng)中所有正確構件文本數(shù)的比率，它反映了該構件庫中實有的相關構件量在多大程度上可以被正確檢出。

其中，Dr表示檢索出的正確構件文本數(shù)，Dt表示所有正確構件文本數(shù)。

查準率（P）：檢索系統(tǒng)在進行某一檢索時，檢索出的正確構件文本數(shù)與檢索出的構件文本數(shù)的比率，它反映了每次從該構件庫中實際檢出的全部構件中有多少是相關的。

P=Dr/Da（12）

其中，Dr表示檢索出的正確構件文本數(shù)，Da表示檢索出的構件文本數(shù)。

3.2實驗結果與分析

該實驗是當構件庫中新增加一個構件時，基于LSA構件檢索算法和基于增量式LSA構件檢索算法對構件庫中構件檢索的查準率、查全率和查詢效率的比較，結果分別見圖1、圖2、圖3。

從圖1和圖2可以看出，基于增量式LSA構件檢索算法與基于LSA構件檢索算法的查準率和查全率基本相似。從圖3可以看出，本文提出的基于增量式LSA構件檢索算法時間性能上明顯優(yōu)于基于LSA構件檢索算法。原因主要是對更新后的文檔-詞條矩陣進行奇異值分解時，利用了更新前的分解結果，避免了重新進行一次奇異值分解的重復計算。

4　結語

本文提出了一種增量式潛在語義分析的構件檢索算法，克服了當構件庫的規(guī)模逐漸增大時，運算復雜度較高的弊端。實驗結果表明，該算法能夠提高構件檢索效率，有利于軟件復用。但是本文只考慮了向構件庫中添加構件的情況，因此，下一步將研究從構件庫中刪除構件的情況。

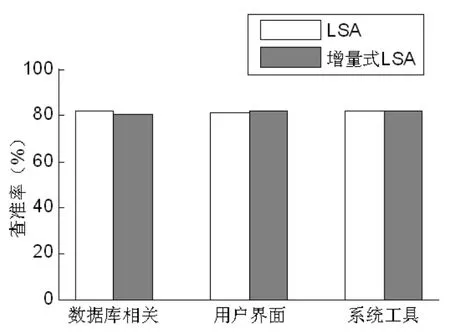
圖1　兩種構件檢索算法查準率的比較

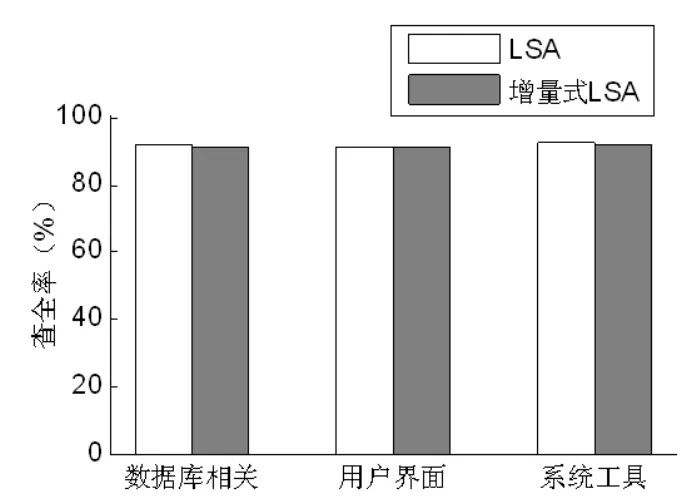
圖2　兩種構件檢索算法查全率的比較

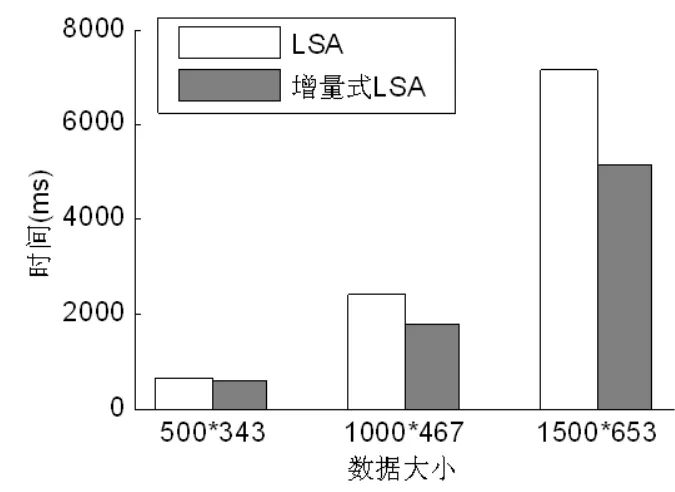
圖3　兩種構件檢索算法效率的比較

[1]任姚鵬,陳立潮等.基于潛在語義分析的構件聚類改進方法[J].計算機工程,2011,37(4):67-68.

[2]張玉芳,彭時名,呂佳.基于文本分類的TFIDF方法的改進與應用[J].計算機工程,2006,32(19):76-78.

[3]劉大昕,趙磊,王卓.一種基于刻面分類和聚類分析的構件分類檢索方法[J].計算機應用,2004,24(2):89-90.

[4]Dumais S T.Using Latent Semantic Analysis to Improve Information Retrieval[C].Proceedings of the ACM Conference on Human Factors in Computing Systems.Washington D.C.USA:ACM Press,1988:281-285.

[5]James R.Bunchand Christopher P.Nielsen.Updating the Singular Value Decomposition.Numer.Math,1978,31:111-129.

[6]M.Gu,S.C.Eisenstat.A Stable and Fast Algorithm for Updating the Singular Value Decomposition.Tech.Report,RR-966,Yale University,1994.

[7]趙鑠乂.基于MapReduce的奇異值分解方法研究[D].武漢:華中科技大學,2014.

Latent Semantic Analysis;Incremental;Component Retrieval;VSM

Component Retrieval Algorithm Based on Incremental Latent Semantic Analysis

ZHU Yang-kai，GAO Mao-ting

（College of Information Engineering,Shanghai Maritime University,Shanghai 200000）

The spatial and time complexity of the component retrieval method based on latent semantic analysis is increased while the application scale is gradually increasing.Proposes an incremental latent semantic analysis method to avoid duplication by using the result of the decomposition of the last step to do the singular value decomposition for the incremental matrix.Experimental results show that this method can improve the retrieval efficiency of the component.

1007-1423（2016）32-0020-06

10.3969/j.issn.1007-1423.2016.32.005

祝仰凱（1991-），男，河南濮陽人，碩士研究生，研究方向為為軟件工程

高茂庭（1963-），男，博士，教授，系統(tǒng)分析員，CCF高級會員，研究方向為智能信息處理、數(shù)據(jù)庫與信息系統(tǒng)

2016-08-16

2016-10-16