風電葉片雙錘激振加載振動耦合特性及試驗研究

廖高華，烏建中，來鑫

?

風電葉片雙錘激振加載振動耦合特性及試驗研究

廖高華1, 2，烏建中1，來鑫1

(1. 同濟大學機械與能源工程學院，上海，201804；2. 南昌工程學院機械與電氣工程系，江西南昌，330099)

針對風電葉片雙錘激振加載過程出現振動耦合特性，對葉片疲勞加載系統進行合理簡化，基于拉格朗日方程建立動力學數學模型。利用小參數周期平均法對其在共振條件下的幅頻特性進行求解，通過相平面法得到振動系統的耦合特性及穩定性條件，對系統振動耦合過程主要影響參數進行數值仿真。在此基礎上對系統耦合同步傳動、動態分岔耦合、振動耦合同步控制、葉片加載過程進行試驗研究，驗證理論分析的正確性及控制的有效性，為進一步開發高效的風電葉片疲勞加載試驗系統，提供理論支持和試驗依據。

風電葉片；疲勞試驗；雙錘激振；耦合

疲勞損傷是導致葉片損壞的主要原因之一，只有進行全尺寸葉片的疲勞測試才能提供對設計的可靠確認[1?2]。國外風電產業技術發展和應用起步較早，對于葉片疲勞相關問題的分析也進行了大量的研究探討，積累了較多的檢測經驗，目前丹麥LM公司、美國NREL和荷蘭WMC等對多軸和多點加載等新方法進行研究[3]。國內風電設備產業雖然發展較晚，但風電葉片疲勞試驗檢測技術有較快發展，檢測技術研究已進入行列先進，風電葉片檢測已經形成外資企業、民營企業、研究院所等多元化的投資形式。由于設備成本低等優點，中國科學院工程熱物理研究所、上海玻璃鋼研究院等單位采用偏心塊共振加載模式進行單點單軸疲勞加載試驗[4]。偏心塊結構的加載系統由疲勞加載支座、偏心質量塊、葉片夾具、電機、減速箱及電控系統等組成，偏心塊加載裝置與葉片之間通過木鞍相連[5]。大型風力發電機組是我國和世界發達國家未來幾年的發展趨勢，隨葉片長度的增加，柔度和阻尼耗能的增大，加載設備所需功率也隨之增大。通過增加動力系統關鍵參數偏心塊質量及旋轉臂長所帶來的問題是加載力點與葉片間偏矩加大，加載力與葉片耦合更嚴重，且設備成本增加。錘聯動激振加載風電葉片，對葉片施加更合理的加載力，解決了單臺激振錘功率有限的問題，同時葉片受到的試驗載荷更符合設計載荷，縮短試驗時間。在實際應用中，激振加載過程中的存在非線性及動力耦合等問題，其動力學性能變得復雜[6]。激振系統存在主共振、次諧波以及超諧波共振，在共振情況下，較小幅度的外部激勵就會產生很大的響應，甚至會出現跳躍現象。基于上述原因，本文作者對兩偏心塊驅動疲勞加載系統，建立動力學數學模型，求解系統的幅頻特性，研究加載系統的振動行為，分析其在共振條件下的耦合特性及穩定性條件，得出基本的耦合規律，并通過試驗研究，驗證理論分析的正確性及控制的有效性。

1 系統動力學模型及求解

在疲勞加載系統中，加載裝置與風電葉片之間通過夾具相連。根據文獻[5, 7]，對系統建模時作了如下合理假設：1) 葉片近似為線性彈性體，葉片在振動過程中受到彈性力及阻尼力作用，剛度系數為分段函數，不同范圍內具有不同的彈性系數，且葉片黏性阻尼起主要作用，葉片豎直方向的阻尼力和彈性力分別為速度和位移的線性函數；2) 連接夾具與加載源均為均質剛體，葉片做平面運動。在上述假設前提下，根據疲勞加載試驗過程，建立系統動力學模型如圖1所示。圖1中為振動體質心，建立基礎坐標系，力學模型為一種具有對稱非線性彈性的系統，單位質量上彈性力函數()。

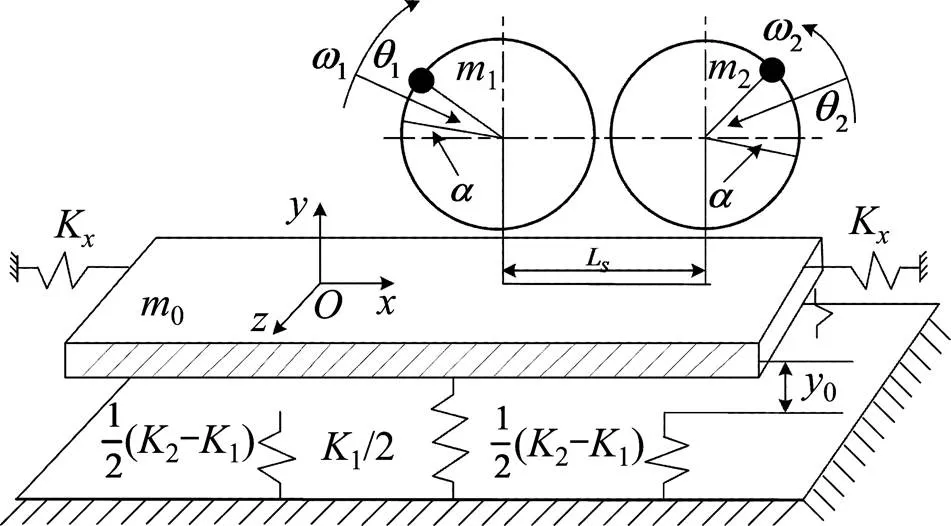
圖1 葉片激振力學模型

1和2為激振錘質量塊的質量，0為葉片質量，由于激振錘裝置與葉片之間沒有相對位移，故將其看成整體，為振動體總質量，，1和2為葉片單位質量上的剛度系數，，。

(1)

振動體在平面內運動，由達朗貝爾力學原理可得加載系統的振動方程為

疲勞加載系統采用三相異步電機，基于其二相同步旋轉坐標系下的數學模型，狀態方程[8]可表示為：

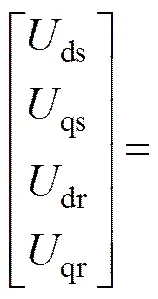
(3)

(4)

式(2)~(4)構成了兩錘激振加載系統振動耦合數學模型。從數學模型上看是一個多變量耦合的非線性系統，加載系統與葉片運動之間存在著相互耦合關系。

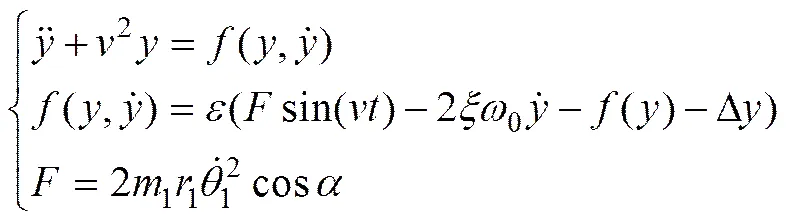
利用平均法[9]對式(5)進行求解，每一個周期內認為其振動為簡諧振動，但下一個振動的振幅與相位角發生微小的改變。設解為

(7)

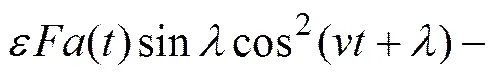
(8)

式中：

,

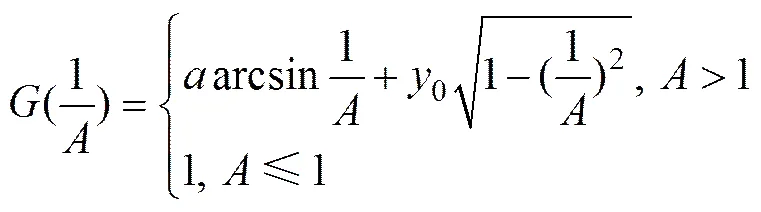
通過式(10)繪出疲勞加載激振系統幅頻與相位差之間特性曲線簇，如圖2所示。由圖2中曲線變化趨勢可以看出：由于系統的彈簧剛度發生變化，使得系統的固有頻率曲線發生偏移。隨著相位差減小，振幅加大，系統的非線性特性越明顯。幅頻曲線中的段為不穩定部分，位移出現了振幅跳躍等現象。

圖2 振動幅頻特性曲線簇

Fig. 2 Amplitude frequency characteristic curves

2 機電耦合特性及穩定性條件

振動耦合產生的外因是振動狀態影響電機負載轉矩的變化，取一個振動周期內負載轉矩的平均值反映耦合規律。由非線性平均法的思想，和在一個周期內近似地看成不變，由式(6)可得振動加速度，第臺激振錘偏心塊所受的負載轉矩為

由式(11)可知：外負載特性與振動系統的幅頻特性曲線相關，激振系統的振動特性會直接影響電機的外負載特性，造成了耦合的特殊性，振動加速度也會出現跳躍以及電機外負載會出現突變。

對于葉片加載系統激振錘的電機軸系，其運動方程可表示為

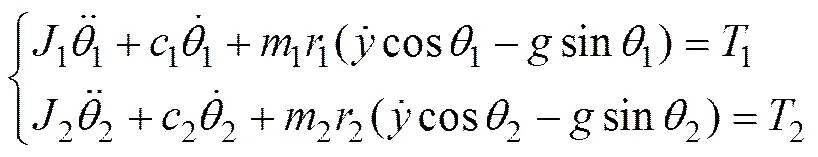
式中：1和2分別為電機1和電機2旋轉軸的轉動慣量；1和2分別為電機1和電機2旋轉軸的阻尼系數；1和2分別為電機1和電機2旋轉軸的電磁轉矩；11和22為旋轉偏心塊的偏心矩。

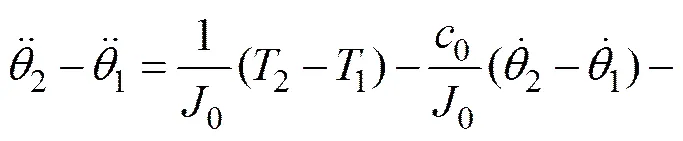
(13)

(14)

式(14)的雅克比矩陣為：

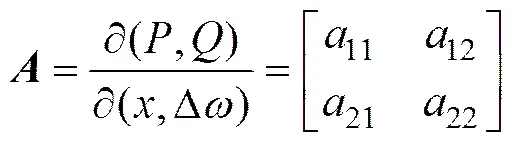
設：

(16)

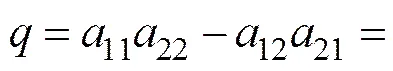
(17)

＞(19)

由式(19)可知：當系統的振動狀態與振動參數滿足一定關系時，相位差趨近于某固定值[10]。加大偏心矩m00、轉動慣量0及振幅，減小旋轉軸的阻尼系數0，并且要盡量使用運行特性一致、參數相同的電機(盡量小)，有利于系統的穩定性。

3 系統振動耦合特性數值仿真

采用Matlab/Simulink軟件對理想狀態下加載過程進行數值仿真。參考IEC 61400?23風電機組葉片規范與文獻[7, 11]，仿真時以9 m葉片為參考加載對象，選取葉片疲勞加載系統的擺錘質量1=30 kg，葉片質量2=360 kg，在葉片兩加載點處的剛度系數近似為1=15.8 kN/m，2=17.5 kN/m，阻尼近似為350 (N?s)/m。假定兩激振錘的機械結構、幾何尺寸、電機性能等參數一致，進行數值仿真。

當兩激振錘電機轉速相等的仿真結果如圖3所示。由圖3可以看出：在理想情況下相位差會逐步收斂于0 rad，并且電機轉速在一定范圍內越高，收斂的速度越快，但當電機的轉速達到400 r/min時，相位差會趨于非零值，如圖3(a)所示，說明能使相位差收斂于0 rad的電機轉速有極限值，該值與葉片參數、加載系統參數等密切相關。設定不同初始相位差的仿真結果如圖3(b)所示，在不同的初始相位差的情況下，相位差都能趨于0 rad或某個固定值，初始相位差越小，收斂速度越快。

根據GL風電機組規范葉片標準，激振錘2固定在葉片展向70%處，激振錘1在葉片展向位置小于激振錘2，且兩者之間的安裝距離s，兩電機的轉速皆設置為210 r/min。圖4所示為兩激振錘之間的安裝距離s對耦合的影響。由圖4可知：隨著安裝距離s的加大，相位差趨于0 rad或某個固定值的趨勢越強。當兩激振錘安裝距離越大時，振動狀態中偏轉振動占有的成分加大，相位差有趨于0 rad的趨勢。

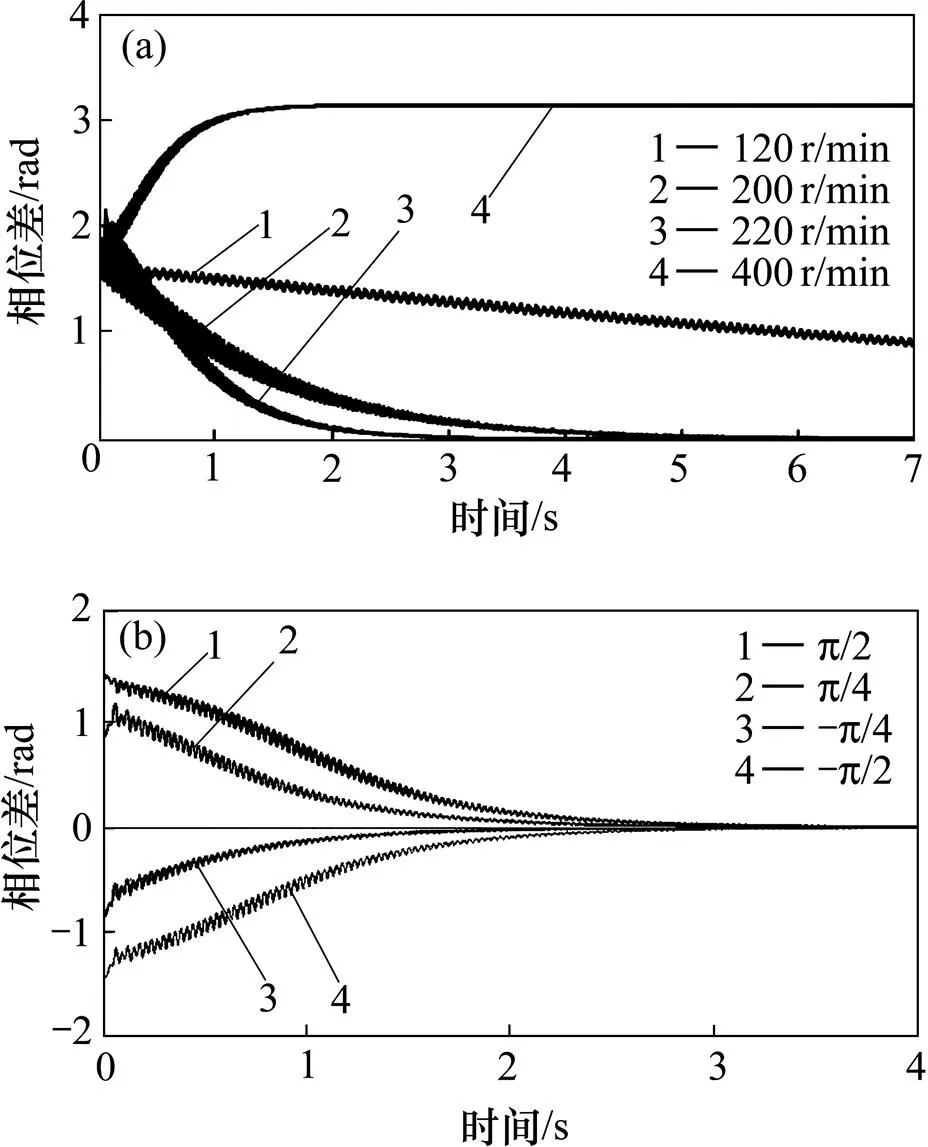
(a) 不同轉速時相位差；(b) 不同初始相位差時相位差

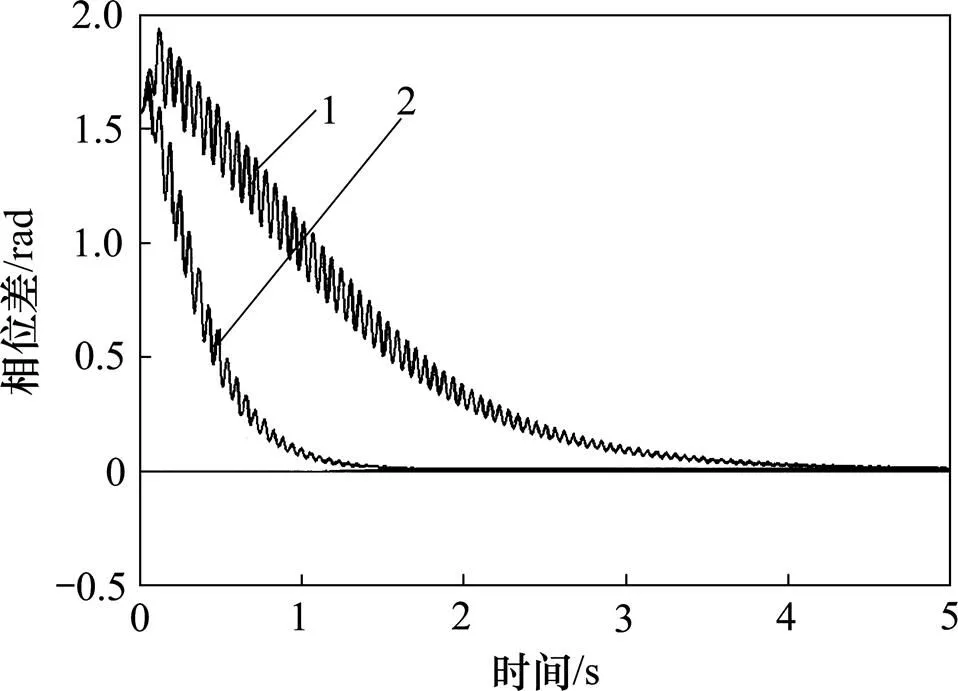
Ls/m：1—0.5；2—1.0。

不同驅動頻率對系統同步加載時，葉片振幅曲線如圖5所示。當兩激振錘回轉速度相同并接近于葉片固有頻率(轉速220 r/min)時，振動趨于同步，葉片振幅會由最初的波動狀態逐漸趨于穩定，如圖5(a)所示，這種振動現象是“加載驅動源?葉片”之間振動耦合的結果。兩激振錘與葉片固有頻率相同時發生共振現象，葉片幅值迅速上升到最大，若兩者頻率相差較大，偏離共振時的轉速約為180 r/min，葉片振幅則出現較大的波動，如圖5(b)所示。

4 試驗研究

將風電葉片固定在疲勞加載基座上，利用支架和葉片夾將兩加載裝置固定在葉片上，兩疲勞加載裝置分別固定在距離葉片根部65%及45%處。齒輪測速傳感器實時檢測偏心塊的位置信號，送入控制器，控制器實時計算出相位差及電機速度，掃描捕捉葉片的共振點，激光測距儀監測葉片加載點處位移，葉片兩錘激振加載裝置如圖6所示。

圖6 雙激振加載試驗裝置

耦合同步傳動試驗時，雙錘激振裝置中只有1臺啟動，假設改變激振錘1的轉速a(a=220 r/min時，振動頻率等于共振頻率3.67 Hz)，測量兩激振錘的轉速及相位差信息，試驗結果如圖7所示。

從試驗結果可知：當a=210 r/min時，耦合作用激振錘2轉速經過較大的波動后進入同步耦合狀態，如圖7(a)所示；當a＜210 r/min時，激振錘2的運動較為微弱和混亂，不能實現與激振錘1的轉速同步；當a＞250 r/min時，能激發激振錘2的運動，但兩激振錘轉速變化較紊亂，如圖7(c)所示，不能實現同步耦合傳動。當210＜a＜250 r/min時，能夠實現耦合同步傳動，當a=220 r/min時，較容易實現耦合同步傳動，相位差最后穩定在附近小波動，如圖7(d)所示，實現了同步耦合傳動。在共振點較容易滿足同步性條件，低于共振點不能實現同步傳動的原因是振幅及振動加速度較小，不足以維持系統的同步運轉。

對于加載系統激振的葉片為非線性對象，共振點偏離系統固有頻率，可能會出現振幅跳躍等現象的動態分岔，電機的轉速發生突變，相位差急劇變化，進而影響系統的振動狀態。通過試驗驗證分岔耦合現象的存在，試驗時改變電機的轉速(激振錘頻率)，通過測試葉片振幅變化達到驗證動態分岔耦合的目的。圖8所示為試驗測試得出的各激振頻率下的振幅曲線，頻率較低時振幅曲線較平穩，且幅值較小；當激振頻率等于系統的固有頻率3.67 Hz(轉速220 r/min)時具有最大的穩定振幅，而激振頻率超過共振頻率達到 4 Hz(轉速240 r/min)附近時，振幅出現突變，5 Hz時不會出現振幅的突變，并且振幅較小。試驗結果與理論推導吻合，證明了存在動態分岔耦合現象。

兩錘激振葉片時，當滿足同步性條件[12]，兩激振錘的轉速與相位趨于同步，相位差會自動趨于某個固定值。控制同步是實現錘聯動激振加載的有效方式之一，圖9所示為控制同步下的相位差實測曲線，試驗時同步控制策略與算法采用虛擬主令控制方式[13]。在控制作用下相位差能維持在零附近，能消除自同步帶來的固定相位差，在滿足電機功率的條件下對激振系統的同步控制是可行的。

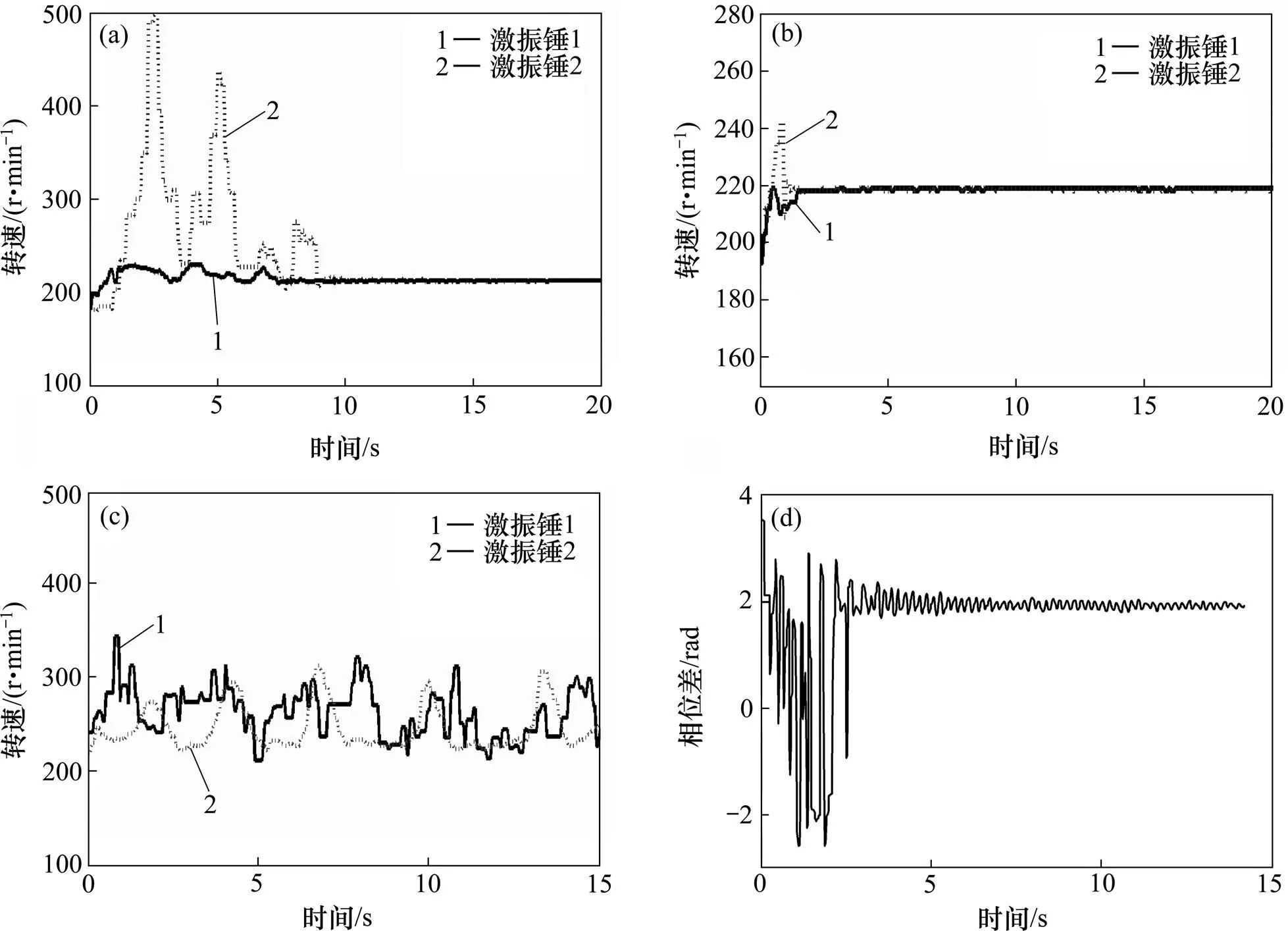
(a) na=210 r/min；(b) na=220 r/min；(c) na=260 r/min；(d) 同步時的相位差曲線

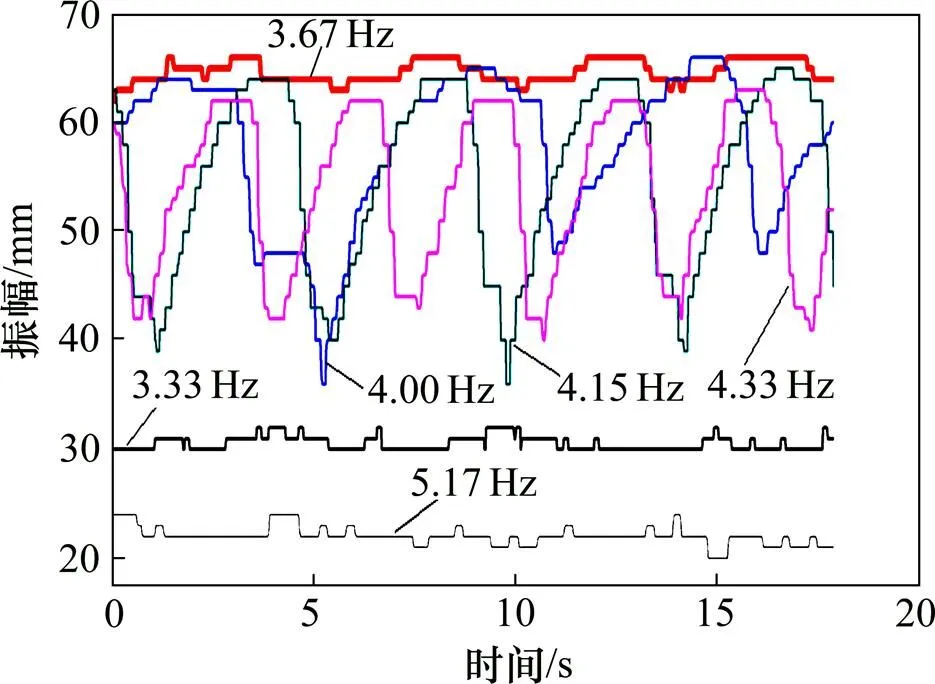
圖8 各種頻率下的振幅測量曲線

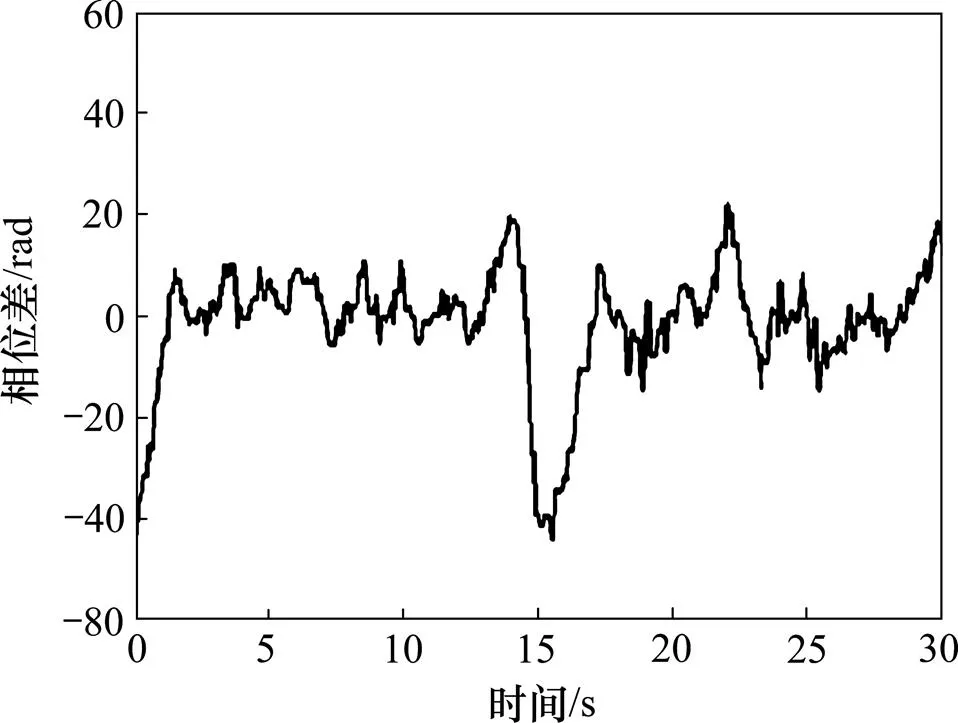
圖9 控制同步的相位差曲線

采用控制同步方式，兩激振錘偏心塊回轉驅動速度為200 r/min(頻率3.33 Hz)，低于葉片的低階固有頻率，并且偏離共振的轉速較小，約為20 r/min，葉片振幅在經歷較大的波動之后，值趨于平穩，此時葉片的振幅僅維持在300mm左右，出現了數值仿真中的同步現象，葉片振幅變化曲線如圖10所示。葉片在受迫振動時，葉片振動頻率并不總等于激振頻率，當激振頻率大于某個值(本次頻率掃描試驗轉速約為190 r/min)時，葉片振動頻率基本等于激振頻率。

圖10 葉片振幅曲線(頻率為3.33 Hz)

5 結論

1) 雙錘激振疲勞加載系統幅頻曲線與系統剛度系數變化、兩激振錘的相位差有關系，外負載特性與幅頻特性曲線相關，使用運行特性一致、參數相同的電機，加大偏心矩、振幅、轉動慣量，減小旋轉軸的阻尼系數以有利于系統的穩定性。

2) 激振錘之間相位差的變化與電機轉速、安裝距離以及葉片的參數等因素密切相關，激振裝置與葉片之間存在著較強的力與能量的傳遞，激振頻率與葉片固有頻率偏差較小時，固存的機電耦合現象會導致葉片振幅穩定，若偏差增大，葉片振幅則發生劇烈波動。

3) 在共振點附近可能會出現動態分岔耦合現象，不同于激振錘的頻率跳變現象，分岔耦合是由于葉片的非線性振動特性造成的，通過工作頻率避開分岔點或控制的方式可避免轉速波動到分岔區。

4) 兩激振錘之間通過同步性轉矩將能量傳遞，轉速變化使之達到平衡穩定狀態，相位差趨于零或固定值，并與系統的固有頻率、非線性程度、電機參數、電磁轉矩差相關。在滿足電機功率的條件下對雙錘激振系統控制可取得較好的同步效果。

參考文獻：

[1] JENSEN F M, FALZON B G, ANKERSEN J, et al. Structural testing and numerical simulation of a 34 m composite wind Tuthine blade[J]. Composite Structures, 2006, 76: 52?61.

[2] 李德源, 葉枝全, 陳嚴, 等. 風力機葉片載荷譜及疲勞壽命分析[J]. 工程力學, 2004, 21(6): 118?123. LI Deyuan, YE Zhiquan, CHEN Yan, et al. Load spectrum and fatigue analysis of the blade of horizontal axis wind turbine[J]. Engineer Mechanics, 2004, 21(6): 118?123.

[3] SHAMSAEI N, GLADSKYI M, PANASOVSKYI K, et al. Multiaxial fatigue of titanium including step loading and load path alteration and sequence effects[J]. International Journal of Fatigue, 2010, 32(11): 1862?1874.

[4] 石可重, 趙曉路, 徐建中. 大型風電機組葉片疲勞試驗研究[J]. 太陽能學報, 2011, 32(8): 1264?1267.SHI Kezhong, ZHAO Xiaolu, XU Jianzhong. Research on fatigue test of large horizontal axis wind turbine blade[J]. Acta Energiae Solaris Sinica, 2011, 32(8): 1264?1267.

[5] 張磊安, 黃雪梅. 風電葉片單點疲勞加載過程數值仿真與試驗[J]. 振動、測試與診斷, 2014, 34(4): 732?736.ZHANG Leian, HUANG Xuemei. Simulation and test of wind power blades single point fatigue loading process[J]. Journal of Vibration, Measurement & Diagnosis, 2014, 34(4): 732?736.

[6] 劉冠麟, 鄂加強, 張彬. 兆瓦級風電機組風力槳葉多學科設計優化[J]. 中南大學學報(自然科學版), 2013, 44(1): 140?148.LIU Guanlin, E Jiaqiang, ZHANG Bin. Multi disciplinary optimization design on blades of MW wind turbine[J]. Journal of Central South University (Science and Technology), 2013, 44(1): 140?148.

[7] HAUPFEAR W M. The development of an adaptive control system for a phase locked excitation method for advanced wind turbine blade fatigue testing[D]. Daytona Beach: Embry Riddle Aeronautical University, 2010: 21?23.

[8] 王鋒, 姜建國, 顏天佑. 基于Matlab 的異步電動機建模方法的研究[J]. 系統仿真學報, 2006, 18(7): 1733?1741. WANG Feng, JIANG Jianguo, YAN Tianyou. Methods of asynchronous motor model simulation based on Matlab[J]. Journal of System Simulation, 2006, 18(7): 1733?1741.

[9] 李小號, 劉杰, 劉勁濤. 單質體非線性系統諧波銳共振的諧振同步分析[J]. 機械工程學報, 2010, 46(1): 86?91.LI Xiaohao, LIU Jie, LIU Jintao. Analysis of harmonic oscillation synchronization for the single-mass nonlinear system under harmonic wave sharp resonance condition[J]. Journal of Mechanical Engineering, 2010, 46(1): 86?91.

[10] ZHAO Cunyu, ZHANG Yimin, WEN Bangchun, et al. Synchronisation and general dynamic symmetry of a vibrating system with two exciters rotating in opposite directions[J]. Chinese Physics B, 2010, 19(3): 030301?7.

[11] 單光坤, 關新, 宋世東. 100 kW風力發電機葉片疲勞分析[J]. 可再生能源, 2010, 28(2): 21?26.SHAN Guangkun, GUAN Xin, SONG Shidong. Fatigue analysis on blade of 100kW wind turbine[J]. Renewable Energy Resources, 2010, 28(2): 21?26.

[12] 羅春雷, 韓清凱. 液壓驅動控制的偏心回轉系統同步特性[J]. 機械工程學報, 2010, 46(6): 176?182. LUO Chunlei, HAN Qingkai. Synchronization characteristics research of eccentric gyration system controlled by hydraulic driving[J]. Journal of Mechanical Engineering, 2010, 46(6): 176?182.

[13] 來鑫, 烏建中, 周文, 等. 樁錘同步振動系統的機電耦合特性及同步控制[J]. 同濟大學學報(自然科學版), 2012, 40(6): 920?925.LAI Xin, WU Jianzhong, ZHOU Wen, et al. Synchronization control and electromechanical coupling characteristics of pile hammer synchronous vibration system[J]. Journal of Tongji University (Natural Science), 2012, 40(6): 920?925.

(編輯 楊幼平)

Experimental study and coupling characteristics of double hammer excitation fatigue loading system

LIAO Gaohua1, 2, WU Jianzhong1, LAI Xin1

(1. College of Mechanical Engineering, Tongji University, Shanghai 201804, China;2. Department of Mechanical and Electrical Engineering, Nanchang Institute of Technology, Jiangxi 330099, China)

The double hammer excitation fatigue loading system was simplified for the coupling-problem occurring in case of wind turbine blade loading multi-point excitation. The dynamic mathematical model was established based on lagrange equations by using the two eccentrical blocks’ vibration loading as object. Electromechnical coupling equations for the system was constructed and then the electromechanical coupling was solved by using the small parameter cycle average method in resonance conditions. The electromechnical coupling characteristics and stability conditions of vibration system were obtained by the phase plane method. The mechanism of system coupling was revealed. On this basis, the mechanical and electrical coupling characteristics of primary resonance, system dynamic bifurcation coupling and synchronization control were studied. The coupling characteristics of dynamic bifurcation and avoiding method were obtained. Finally, the correctness of theoretical analysis through the test provides guidance for the engineering application of the fatigue loading system.

wind turbine blade; fatigue test; double excitation; coupling

10.11817/j.issn.1672-7207.2016.11.011

TH112

A

1672?7207(2016)11?3692?08

2015?11?10；

2016?02?25

國家自然科學基金資助項目(51505290) (Project(51505290) supported by the National Natural Science Foundation of China)

烏建中，博士，教授，從事機電液控制研究；E-mail: tjjd328 @163.com