基于遺傳算法的壓縮感知DOA測量矩陣設計

楊 潔, 劉朋露

(西安郵電大學 通信與信息工程學院， 陜西 西安 710121)

?

基于遺傳算法的壓縮感知DOA測量矩陣設計

楊 潔, 劉朋露

(西安郵電大學 通信與信息工程學院， 陜西 西安 710121)

基于格拉姆矩陣(Gram matrix)，利用遺傳算法給出一種優化壓縮感知波達方向測量矩陣的方法。對陣元進行不重復采樣，構造測量矩陣；根據稀疏字典得到壓縮感知DOA的感知矩陣，并由其構造格拉姆矩陣；以所得格拉姆矩陣非對角元素的平方和作為遺傳算法的適應度值，利用遺傳算法求解出最佳采樣陣元。仿真實驗顯示，以所給方法設計的測量矩陣，在采樣陣元較少且信噪較低的情形下，仍具有較好的DOA估計性能。

遺傳算法；壓縮感知；波達方向；測量矩陣；格拉姆矩陣

基于陣列稀疏采樣的壓縮感知波達方向(DOA)估計算法,先用測量矩陣對陣列的輸出信號進行壓縮采樣，再借助稀疏恢復算法求得波達方向。解稀疏過程中，稀疏字典須滿足一定正交性關系，且與測量矩陣盡可能地不相關。

測量矩陣包含隨機測量矩陣和確定性測量矩陣。隨機測量矩陣中的高斯矩陣和伯努利矩陣，都能以較大概率滿足有限等距性質(Restrict Isometry Property, RIP)條件。但在實際應用中，隨機數的產生對硬件有很高要求，隨機測量矩陣的壓縮投影和信號重構過程對系統有很高要求，而且，它只在統計意義下，以很高的概率滿足RIP條件和弱相干性，難以保證每次稀疏恢復的精度。隨機矩陣具有不確定性，以及它浪費存儲資源和計算量大的缺點，嚴重影響著壓縮感知DOA的估計結果。

針對測量矩陣與稀疏字典應盡可能不相關的要求，人們給出了許多優化測量矩陣的方法[1-8]。其中，部分優化方案涉及降低相干系數[5]，定義感知矩陣冪平均相關性[6]，引入最小化感知矩陣統計相關系數的波形優化目標函數[7]，或轉而尋求確定性測量矩陣的構造[8]等。

考慮到實際應用中的物理可實現性和計算復雜度，在壓縮感知DOA中構造的測量矩陣，還應盡可能少，且不重復地選取采樣陣元。本文擬結合格拉姆矩陣(Gram matrix)的構造方法[1]，根據整體互相關系數，利用格拉姆矩陣來優化壓縮感知DOA測量矩陣，并利用遺傳算法選取最佳采樣陣元，以求構造出最佳測量矩陣。

1 壓縮感知DOA模型

1.1 陣列信號模型

假設某均勻線陣(Uniform Linear Array, ULA)共有N個陣元,陣元間距為d，采樣點總數為T,采樣時刻t=1,2,…,T。則某采樣時刻t，N個陣元的陣列輸出信號是一個N×1維的向量

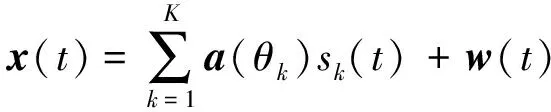
(1)

式中，sk(t)是從θk方向入射的窄帶信號，K為入射的窄帶信號個數；w(t)是一個N×1維的加性高斯白噪聲矢量；a(θk)是N×1維的陣列導向矢量，且

a(θ)=[1,e-jα,…,e-jα(N-1)]T。

其中

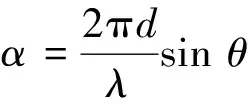
代表同一入射信號到達不同陣元與參考陣元之間的波程差，λ是入射信號的波長。

根據式(1)和(2)，陣列的輸出信號還可表示為

x=As(t)+w(t)。

(3)

式中，A是一個N×K維的陣列流型矩陣，s(t)代表K×1維的窄帶入射信號。根據式(3)，在多個快拍條件下，均勻線陣的陣列輸出信號可表示為

X=AS+W。

(4)

式中，X為N×T維的陣列輸出信號，S為K×T維的窄帶入射信號，W為N×T維的加性高斯白噪聲矩陣。

1.2 陣列的稀疏采樣模型

單快拍條件下[9],假設x是一個N×1維的信號矢量,且

x=Ψz。

其中:Ψ是一個N×M維的稀疏字典，即x是K稀疏的，且K?M(K為來波個數)；z是一個M×1維的稀疏向量，其中有K個非零元素。壓縮感知理論表明[9]，x能夠從測量矢量y中恢復出來，即

y=Φx=ΦΨz=ACSz。

(5)

式中:y是一個m×1維的測量矢量；Φ是一個m×N維的測量矩陣，一般由隨機矩陣構成(即高斯矩陣或伯努利矩陣)通過它可以隨機地對陣元進行采樣，構造測量矢量y；ACS是由Φ和Ψ相乘得到的感知矩陣；z是x在稀疏字典Ψ下的稀疏表示系數。利用正交匹配追蹤算法(OMP)[10],可以對式(5)進行求解。

多快拍條件下，假設均勻線陣的陣列模型仍如式(4)所示，則壓縮感知框架下的陣列輸出信號可以表示為[9]

X=ΨZ+W。

(6)

式中:Ψ是一個N×Ns維的稀疏矩陣，Ns代表空域劃分網格數；Z是一個Ns×T維的矩陣，其中每一列都是K稀疏的，即每一列中有K個非零元素，其包含著來波方向信息；W是加性高斯白噪聲矩陣。

根據式(6)，假設測量矩陣Φ已知，那么多快拍條件下陣列的稀疏采樣模型可以表示為

Y=ΦX=ΦΨZ+ΦW。

(7)

式中，Y代表測量矩陣對陣列進行壓縮采樣后的數據信息。

為了綜合每個采樣快拍下的DOA估計結果，對Y中每個快拍下的數據運用稀疏恢復算法求解出DOA信息[9]。綜合每個快拍下的數據信息得出DOA估計結果

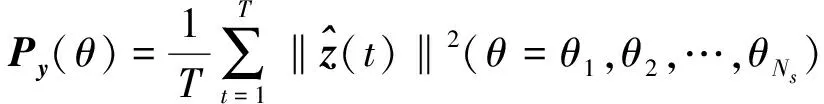
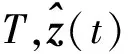
2 優化模型的構造

假設某陣列共有N個陣元，抽取M個陣元來構造壓縮感知DOA測量矩陣。記Q為索引集合，即所選取陣元所有可能組合方式的集合,EQ為選取的采樣陣元所對應的單位矩陣中的每一行構成的測量矩陣。從N階單位陣I抽取其中不同的M行，構造M×N階測量矩陣EQ，即

Φ=EQ。

(8)

根據式(5)可知

ACS=ΦΨ=EQΨ。

(9)

進而得Gram矩陣

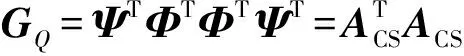
(10)

在測量矩陣優化理論中，采用整體互相關系數來衡量測量矩陣和稀疏字典的不相干性。互相干系數C定義為Gram矩陣非主對角線元素的平方和。根據式(10)，可得

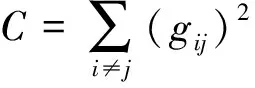
(11)

其中,gij是所構造的Gram矩陣GQ的元素。

整體互相關系數代表了測量矩陣和稀疏字典的相干性，相干系數越小，相同稀疏恢復算法的情況下，稀疏恢復精度越高。

綜上所述，基于Gram矩陣的壓縮感知DOA測量矩陣優化模型，可以表示為優化問題

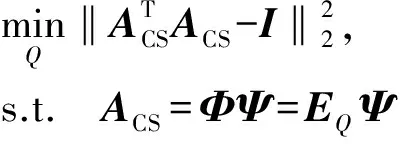
(12)

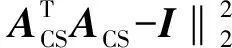
3 測量矩陣的優化

遺傳算法在解決組合優化問題時具有明顯優勢，它能仿照生物進化和遺傳的特點，依據優勝劣汰的自然進化法則，最大限度地保持樣本的多樣性，并能在解空間的不同區域內進行多點搜索，通過反復迭代，在全局范圍內搜尋優化問題的最優解，保證以最大概率得到全局最優解[11-12]。

考慮使用遺傳算法來優化測量矩陣。設遺傳算法的最大迭代次數為Lmax,種群個數為Npop，交叉概率為Pc，變異概率為Pm。現將遺傳算法與組合優化模型(12)相結合，選取最佳采樣陣元。

3.1 初始化種群

利用Matlab中的randperm函數產生1～N之間兩兩不等的M個整數，代表所選取的采樣陣元，即得到索引集合Q中一種采樣陣元組合方式。根據由此產生的隨機數，構造一個長度為N的行向量V，其中所選采樣對應的元素為1，其余元素為0。仿此隨機產生Npop個行向量Vi(i=1,2,…,Npop),從而構造出一個Npop×N維的矩陣,即初始種群。

3.2 計算適應度

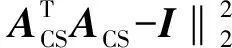
3.3 選擇遺傳個體

選擇適應度值最小的遺傳個體作為最優個體，將最優遺傳個體保存起來。按照“輪盤賭”的方法選出下一步操作，即交叉和變異，所需要的遺傳個體。其中，保存下來的最優遺傳個體不進行后續的交叉和變異操作。

3.4 交叉

根據所選擇的遺傳個體，產生長度為M-1的一個交叉概率序列，將其逐一與交叉概率Pc作比較，小于Pc者對應的N1個遺傳個體作為交叉種群。若N1為奇數，則從未被選擇的遺傳個體中隨機選出一個遺傳個體加入交叉種群。對交叉種群中兩個相鄰的遺傳個體進行交叉操作。交叉操作時，預先產生一隨機交叉位，即從1～N中隨機抽取一個整數，交換相鄰兩個遺傳個體從隨機交叉位至最末位的元素。隨機交叉位的選擇，須保證參與交換的元素中具有相同數量的元素1，即采樣陣元相當；否則，重新選擇隨機交叉位，直至滿足該條件。

3.5 變異

根據所選擇的遺傳個體，產生長度為M-1的一個變異概率序列，將其逐一與變異概率Pm作比較，小于Pm者對應的N2個遺傳個體作為變異種群。對變異種群中的遺傳個體進行變異操作，即隨機剔除各遺傳個體對應采樣陣元中的一個，并隨機加入一個其余陣元。

3.6 循環

合并經交叉和變異操作后的遺傳個體與所保存的最優遺傳個體，構成新的種群，重新開始適應度計算等操作步驟。根據預先設定好的循環終止條件，即由遺傳算法的最大迭代次數Lmax，判斷是否終止循環。

循環終止后，可以得出最優的適應度值及其對應的最優遺傳個體。采用Gram矩陣優化測量矩陣時，其最優遺傳個體對應的采樣陣元分布方式是均勻線陣。相比于均勻線陣，在非均勻線陣下利用OMP算法進行稀疏恢復，能獲得更高的稀疏恢復精確度[13],故也可考慮采用次優解替代最優解構造測量矩陣。稱這種替代方法為Gram矩陣構造測量矩陣的修正，即Gramfix測量矩陣。

4 仿真結果

假設均勻線陣共有36個陣元，陣元間距為入射信號的半波長，不重復地抽取10個陣元作為陣列的稀疏采樣陣元，構造測量矩陣。設定遺傳算法的最大迭代次數為1 500，種群大小為40，個體串長度為陣元個數36，交叉概率為0.8，變異概率為0.05。以等角度劃分方式構造稀疏字典Ψ，其空域劃分網格數為181。根據所構造的測量矩陣優化模型，結合遺傳算法，優化測量矩陣。

仿真所得最優適應度值變化曲線如圖1所示，遺傳算法在迭代到530代時，其最優適應度值不再發生變化。所選取的最優采樣陣元分布為

6,9,12,15,18,21,24,27,30,33,

次優采樣陣元分布為

6,8,13,16,17,20,24,26,31,33。

由此可見，所給方法是可行有效的。

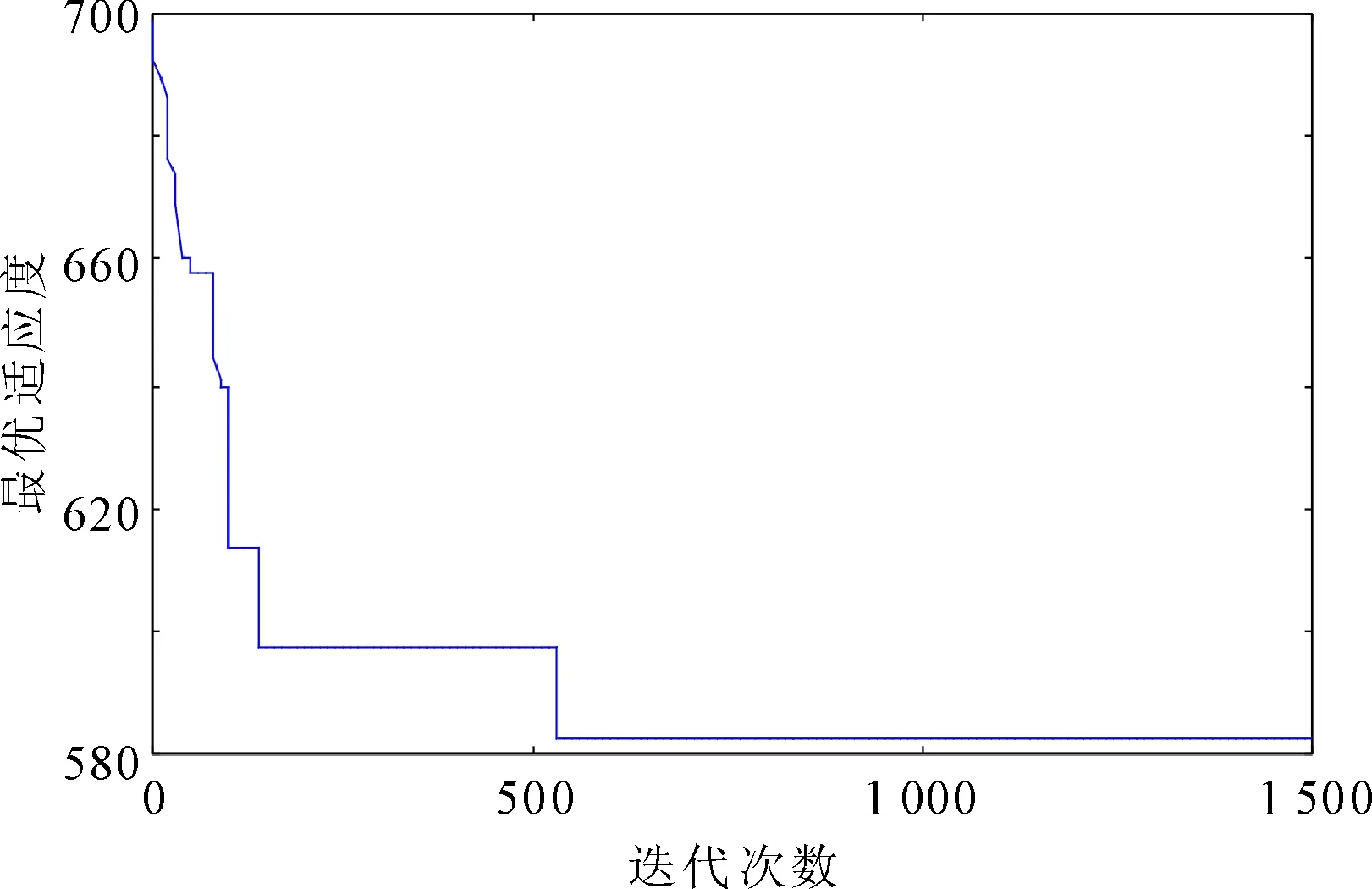
圖1 最優適應度隨迭代次數的變化

為比較Gram矩陣，Gramfix矩陣和伯努利隨機矩陣的優化性能，采用相同陣列結構,并引入來波角度分別為-10°, 25°，60°的3個遠場窄帶入射信號，進行仿真。稀疏字典的空域仍按等角度劃分為181個網格，陣列的采樣快拍數取為60。當信號角度的估計值與實際值相差不起過1°時，認為估計成功。在信噪比為5 dB的情況下，進行30次獨立重復試驗。3種測量矩陣對應的DOA估計正確概率以及均方誤差，如表1所示。

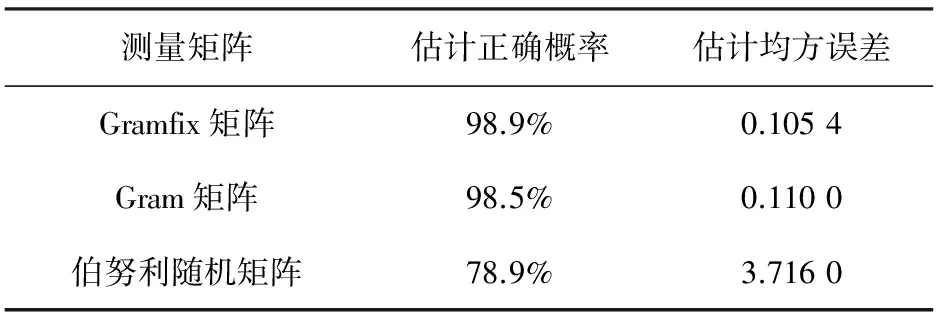
表1 測量矩陣DOA估計結果

在不同信噪比情況下，各進行30次獨立重復試驗，信噪比的取值范圍為-5～21 dB。3種測量矩陣對應的DOA估計正確概率和均方誤差，如圖2所示。由其可見，信噪比較低時，由次最優采樣陣元構造的測量矩陣，其DOA估計正確概率高于兩種測量矩陣，而均方誤差則低于其它兩種測量矩陣。

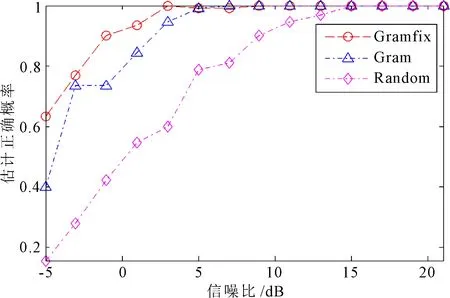
(a) 估計正確概率

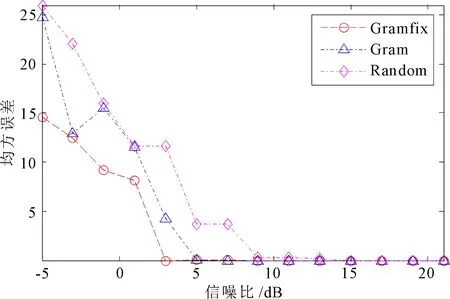
(b) 估計均方誤差

5 結語

通過對陣列陣元進行不重復采樣，構造壓縮感知DOA的測量矩陣,并以測量矩陣與稀疏字典的乘積作為壓縮感知DOA的感知矩陣，再并以格拉姆矩陣為基礎，可構造出壓縮感知DOA的測量矩陣優化模型。

以格拉姆矩陣非主對角線元素的平方和，也即互相干系數，作為遺傳算法的適應度值，將遺傳算法與優化模型相結合，通過遺傳算法求解最佳采樣陣元，即得最佳測量矩陣設計。

仿真實驗顯示，所設計的測量矩陣較隨機測量矩陣在DOA估計方面具有更好性能。不過，當天線陣元較多時，采用遺傳算法來優化測量矩陣，還需盡可能地縮短優化時間，以及確保最優解的收斂性。

[1] ENDRA O. Joint optimization of measurement matrix and sparse dictionary in compressive sensing[C/OL]//2012 International Conference on Computer and Communication Engineering (ICCCE). [S.l.]:IEEE, 2012:420-425[2016-01-28].http://dx.doi.org/10.1109/ICCCE.2012.6271222.

[2] LI G, ZHU Z, YANG D, et al. On Projection Matrix Optimization for Compressive Sensing Systems[J/OL]. IEEE Transactions on Signal Processing, 2013,61(11):2887-2898[2016-04-28].http://dx.doi.org/10.1109/TSP.2013.2253776.

[3] JIANG Q R, BAI H, LI D, et al. Alternative optimization of sensing matrix and sparsifying dictionary for compressed sensing systems[C/OL]//2014 IEEE 9th Conference on Industrial Electronics and Applications (ICIEA). [S.l.]:IEEE, 2014:510-515[2016-04-28].http://dx.doi.org/10.1109/ICIEA.2014.6931217.

[4] ELAD M. Optimized Projections for Compressed Sensing[J/OL]. IEEE Transactions on Signal Processing, 2007,55(12):5695-5702[2016-04-28].http://dx.doi.org/10.1109/TSP.2007.900760.

[5] 潘金鳳. 壓縮感知重構技術研究[D/OL].西安:中國科學院西安光學精密機械研究所,2015:24-118[2016-05-20].http://cdmd.cnki.com.cn/Article/CDMD-80142-1016709331.htm.

[6] 李哲濤, 潘田, 朱更明,等. 低冪平均列相關性測量矩陣構造算法[J/OL]. 電子學報, 2014,42(7):1360-1364[2016-04-20].http://dx.chinadoi.cn/10.3969/j.issn.0372-2112.2014.07.017.

[7] 賀亞鵬, 莊珊娜, 李洪濤,等. 基于感知矩陣統計相關系數最小化的壓縮感知雷達波形優化設計[J/OL]. 電子與信息學報, 2011,33(9):2097-2102[2016-04-20].http://dx.chinadoi.cn/10.3724/SP.J.1146.2011.00021.

[8] 王強, 李佳, 沈毅. 壓縮感知中確定性測量矩陣構造算法綜述[J/OL].電子學報, 2013,41(10):2041-2050[2016-04-20].http://dx.chinadoi.cn/10.3969/j.issn.0372-2112.2013.10.027.

[9] WANG Y, LEUS G, PANDHARIPANDE A. Direction estimation using compressive sampling array processing[C/OL]// IEEE/SP 15th Workshop on Statistical Signal Processing. [S.l.]:IEEE, 2009:626-629[2016-04-28].http://dx.doi.org/10.1109/SSP.2009.5278497.

[10] WANG W, WU R. High resolution direction of arrival (DOA) estimation based on improved orthogonal matching pursuit (OMP) algorithm by iterative local searching[J/OL]. Sensors, 2013, 13(9):11167-11183[2016-04-28].http://dx.doi.org/10.3390/s130911167.

[11] 代悅寧, 朱國暉. 基于遺傳算法的LTE下行系統資源分配算法[J/OL]. 西安郵電大學學報, 2014, 19(1):50-54[2016-04-28].http://dx.chinadoi.cn/10.13682/j.issn.2095-6533.2014.01.010.

[12] 閆興亞, 吳加賀, 石云平. 基于遺傳算法的虛擬校園漫游路徑規劃[J/OL]. 西安郵電大學學報, 2013,18(6):80-84[2016-04-28].http://dx.chinadoi.cn/10.3969/j.issn.1007-3264.2013.06.017.

[13] 刁鳴, 高璐, 高洪元,等. 基于非均勻線陣的壓縮感知波達方向估計[J/OL]. 計算機工程, 2015,41(10):83-87[2016-04-28].http://dx.chinadoi.cn/10.3969/j.issn.1000-3428.2015.10.016.

[責任編輯:陳文學]

Design of compressive sensing DOA measurement matrix based on genetic algorithm

YANG Jie, LIU Penglu

(School of Communication and Information Engineering, Xi’an University of Posts and Telecommunications, Xi’an 710121, China)

Based on Gram matrix, a method of optimizing the measurement matrix of compressive sensing DOA is presented by using genetic algorithm. Against array elements to carry out non repeated sampling, and construct the measurement matrix. According to the sparse dictionary, the sensing matrix of compressive sensing DOA is obtained, and the Gram matrix is constructed therewith. Take the sum of squares of the non-diagonal elements in the constructed Gram matrix as the fitness value of the genetic algorithm, and use this algorithm to pick out the Optimum sampling array element. Experimental simulation results show that, even in case of less sampling array element and low signal noise ratio, the measurement matrix given by the presented algorithm is of good DOA estimation performance.

genetic algorithm, compressive sensing, direction of arrival (DOA), measurement matrix, Gram matrix

10.13682/j.issn.2095-6533.2016.06.018

2016-06-30

國家自然科學基金資助項目(61402365)；陜西省科技工業攻關資助項目(2013K06-33)

楊潔(1976-)，女，碩士，副教授，從事信號處理及應用研究。E-mail:yangjie@xupt.edu.cn 劉朋露(1990-),男,碩士研究生，研究方向為信號與信息處理。E-mail:459734560@qq.com

TN911.7

A

2095-6533(2016)06-0093-05