直接數據域空時自適應單脈沖方法

王 璐, 吳仁彪

(中國民航大學智能信號與圖像處理天津市重點實驗室, 天津 300300)

?

直接數據域空時自適應單脈沖方法

王 璐, 吳仁彪

(中國民航大學智能信號與圖像處理天津市重點實驗室, 天津 300300)

機載雷達空時自適應處理(space-time adaptive processing,STAP)與單脈沖技術相結合可以實現對運動目標空、時參數的估計。然而,在非均勻環境下,由于同分布快拍數有限,雜波協方差矩陣難以準確估計,常常導致STAP方法性能急劇下降甚至失效,進而無法有效實現目標檢測和參數估計。本文提出一種直接數據域的動目標空時參數估計方法,該方法首先應用幅相估計譜(amplitude and phase estimation，APES)譜估計由被檢測單元數據估計出雜波干擾協方差矩陣,然后利用STAP技術抑制雜波和干擾,并結合單脈沖理論實現對目標角度和多普勒頻率的估計。仿真結果表明,與傳統單脈沖方法相比,新方法具有自適應抑制雜波干擾的能力和更好的估計性能;同時由于無需參考數據,該方法更適應于非均勻環境。

機載雷達; 空時自適應處理; 單脈沖技術; 非均勻雜波

0 引 言

單脈沖技術[1-2]是獲取目標方位信息的一種常規方法,該方法能夠利用單個回波脈沖信號進行角度估計,并在分辨力上突破波束寬度的限制,是基于代價函數的最大似然(maximum likelihood, ML)方法的近似。為抑制干擾對單脈沖方法的影響,一些學者提出了自適應單脈沖技術[3-4],并研究了主/旁瓣干擾、子陣結構誤差等問題,提出了基于鑒角曲線修正的自適應單脈沖算法[5-6]。

然而,當單脈沖應用于機載相控陣雷達中時,由于下視工作的機載相控陣雷達將接收到分布范圍廣、強度大的地面雜波,使一般的自適應單脈沖技術性能大大降低,甚至失效。同時,由于機載雷達安裝在運動平臺上,其接收的雜波將在多普勒維擴展開來,雜波譜呈現空時二維耦合特性。因此,通常首先采用空時自適應處理(space-time adaptive processing,STAP)技術[7]有效地抑制地雜波,然后在空時二維實施單脈沖技術進行參數估計。文獻[8-9]針對機載相控陣雷達系統提出了一種空時二維自適應單脈沖測角方法,實現了二維自適應濾波與單脈沖測角技術的兼容,且能同時獲得對角度、多普勒頻率參數的估計。但迄今為止，此類空時自適應單脈沖方法在非均勻環境下的應用尚少有討論[10]。

非均勻環境指雜波功率起伏、干擾目標、孤立干擾以及雜波距離相關性等情況隨時間的變化。這將導致STAP處理所需要的滿足獨立同分布(independent and identically distributed, IID)條件的參考數據大大減小[11]。通過對實測數據的分析,人們意識到雜波非均勻性對STAP算法雜波抑制性能的影響非常嚴重[12]。因此,適用于非均勻環境下STAP算法成為研究熱點。當前出現的非均勻STAP算法可以分為以下5類:①功率非均勻抑制法,此類方法假定非均勻性主要表現為雜波功率非均勻,其中一種典型的功率非均勻抑制方法是功率選擇訓練法(power selected training,PST)[13];②非均勻檢測器(no homogenous detector,NHD)[14],此類方法主要用來解決由干擾目標引入的非均勻問題,其中Melvin等人提出用廣義內積NHD來檢測和剔除包含干擾目標的訓練樣本,以改善對雜波協方差矩陣的估計;③直接數據域(direct data domain,DDD)算法[15],此類算法可以僅利用被檢測樣本來消除距離非均勻雜波的影響,但其對被檢測目標的角度、速度參數誤差較敏感;④雜波距離相關性補償法[16],此類方法主要用來解決非正側面陣、共形陣和雙多基地機載雷達中由雜波距離相關性引起的非均勻問題,即雜波多普勒頻率隨著距離的變化而變化的現象;⑤基于先驗信息的STAP方法,此類方法包括參數化STAP方法[17]、結構化STAP方法[18]、基于先驗知識的STAP方法[19]等。這些方法均有力地促進了STAP技術的實用化進程,為非均勻環境下STAP算法與單脈沖技術的結合提供了思路。

本文就非均勻環境下機載相控陣雷達動目標參數估計問題提出一種新方法,該方法直接由被檢測單元數據得到雜波協方差矩陣,再利用空時二維自適應單脈沖技術估計目標空時參數,更適用于機載雷達的應用條件,估計誤差更低;又由于新方法不需要參考數據,所以可以實現在非均勻環境下的應用。

1 問題描述

考慮機載平臺上沿航向方向放置的N元均勻線陣(uniform linear array,ULA),相干處理間隔(coherent processing interval,CPI)內有K個脈沖,假定單個距離門內最多存在一個目標,則被檢測單元的空時快拍為

x=ba(us,ut)+xc+xj+xn

(1)

式中,x,xc,xj,xn均為NK×1的列向量,分別表示被檢測單元內接收的空時數據、數據中的雜波分量、干擾分量和噪聲分量;b表示相應距離單元內目標回波的復幅度;a(us,ut)為目標的空時二維導向矢量,定義為

a(us,ut)=a(ut)?a(us)

(2)

式中，?表示Kronecker積,且時域導向矢量和空域導向矢量分別為

a(ut)=[1exp(jut)exp(j2ut) …exp(j(K-1)ut)]T

(3)

a(us)=[1exp(jus)exp(j2us) …exp(j(N-1)us)]T

(4)

式中,us=2πdcosθ/λ；ut=2πfd/fr表示歸一化空間角頻率和時間角頻率。

本文主要研究的問題是利用式(1)的被檢測距離單元數據(即被雜波、干擾和噪聲污染的空時接收數據)估計出目標的歸一化空間角頻率us=2πdcosθ/λ和時間角頻率ut=2πfd/fr。可以看出兩者由目標所處的方位角θ、系統工作波長λ、目標多普勒頻率fd和脈沖重復頻率fr所決定。因而,估計出歸一化空、時角頻率后即能對目標的角度、速度進行反求,即

(5)

常用的空時二維自適應技術屬于基于統計的方法,是用被檢測單元相鄰的距離單元的數據作為參考數據來估計雜波協方差矩陣,進而抑制地雜波,如文獻[8-9]的空時二維自適應單脈沖處理即屬于這種基于統計的方法。而由于非均勻雜波環境中滿足獨立同分布(independent and identically distributed,IID)的參考數據較少,甚至沒有,使上述方法估計的雜波協方差矩陣與被檢測單元的統計特性偏差較大。這嚴重影響了雜波抑制性能,進而影響了參數估計性能。因此,需要尋找非均勻環境下新的雜波協方差矩陣估計方法。

2 雜波協方差矩陣估計

本節給出一種基于降維處理的直接數據域雜波協方差矩陣估計方法。首先用一個Nt×Kt的空時窗在被檢測單元數據矩陣X上滑動,對被檢測單元數據進行降維處理,如圖1所示,其中Nt和Kt分別表示滑窗的空間和時間維度。

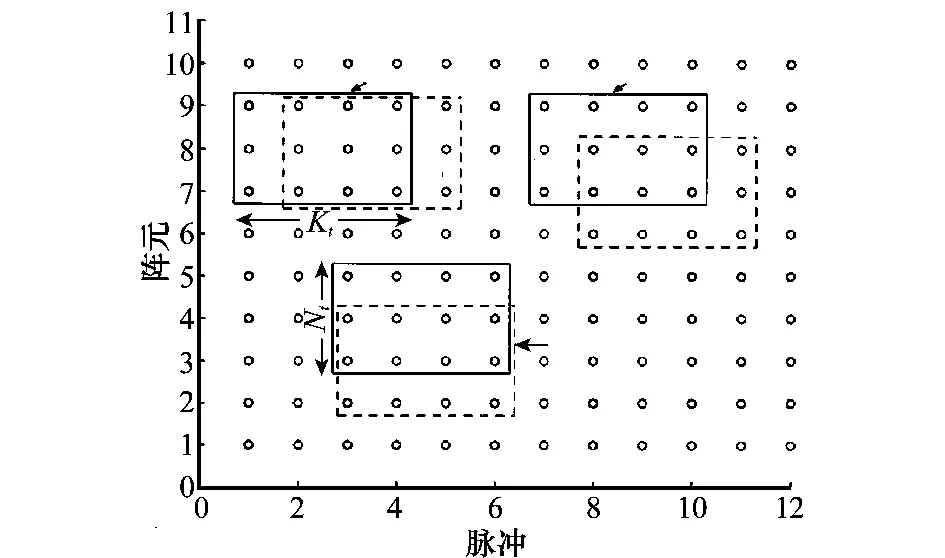
圖1 空時窗在被檢測單元數據上滑動示意圖Fig.1 Sketch map of the space-time window sliding over the primary data

經過在空間向的第m次和時間向的第n次滑動后,乘上相應的相位補償因子,得到的子塊數據如下:

(6)

式中,m=0,1,…,(N-Nt)、n=0,1,…,(K-Kt)。將式(6)中的數據塊按列排成NtKt×1的列向量y(m,n)=vec(Y(m,n)),稱為子快拍,得到總的子快拍數為P=(N-Nt+1)×(K-Kt+1)。這些子快拍含有目標的信息,且能準確反映被檢測單元的雜波、干擾的統計特性。

用這些子快拍計算降維數據協方差矩陣

(7)

式中，Rsub的維度為NtKt×NtKt,該矩陣的理論值應為

Rsub=E{y(m,n)yH(m,n)}=

(8)

(9)

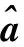
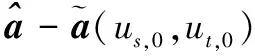
(10)

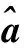
(11)

因此,優化方程式(10)可以簡寫為下面的二次優化問題：

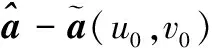
(12)

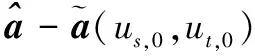
(13)

利用拉格朗日乘數法求解上面的方程,得到目標導向矢量的估計為

(14)

將式(14)代入優化方程式(13)的約束等式,可確定拉格朗日乘子λ的取值滿足下面的關系:

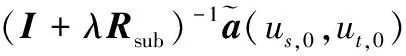
(15)

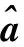
3 空時自適應單脈沖處理

本節結合空時二維自適應單脈沖算法(主要為了解決地雜波問題)和線性約束單脈沖算法(主要為了解決主瓣干擾問題),給出一種適用于嚴重非均勻環境的動目標參數估計方法。

首先,依據常規空時單脈沖處理,當波束指向為(u0,s,u0,t)時,系統的空時2維和波束可表示為

(16)

式中,wΣ(u0,s,u0,t)為和波束的空時2維加權矢量,該矢量的選擇將影響系統和波束的雜波抑制能力、主副瓣參數等。類似地定義空域差波束和時域差波束

(17)

(18)

式中,ws(u0,s,u0,t),wt(u0,s,u0,t)分別為相應的空域差波束及時域差波束的空時2維加權矢量。再定義空域單脈沖比Fs(us,ut)和時域單脈沖比Ft(us,ut)分別為

Fs(us,ut)=Re(Δs(us,ut)/Σ(us,ut))

(19)

Ft(us,ut)=Re(Δt(us,ut)/Σ(us,ut))

(20)

式中，Re(·)表示取實部。對式(19)和式(20)在波束指向(u0,s,u0,t)附近進行Taylor展開

+

(21)

(22)

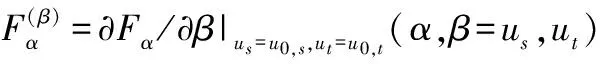
(23)

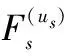
(24)

式中,ks和kt分別為波束指向(u0,s,u0,t)上的靜態空域及時域單脈沖鑒角率。

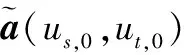
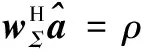
(25)

對于空域差波束加權矢量ws(us,0,ut,0),應滿足使得殘余雜波能量最小化的同時,在單脈沖比、單脈沖鑒角率、互單脈沖鑒角率等方面與靜態時保持一致,即求解優化問題

s.t.Fs(us,0,ut,0)=0

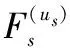
(26)

式中,ks為波束中心處的靜態空域單脈沖鑒角率。

(27)

(28)

因此,式(26)可化簡為

(29)

解式(29)得到空域差波束加權矢量為

(30)

同理可以得到時域差波束加權矢量為

(31)

式中,gt=[0, 0,kt],kt為波束中心處的靜態時域單脈沖鑒角率。

為補償降維處理造成的信息損失,進一步提高參數估計準確性,對被檢測單元數據進行滑動平均處理

(32)

式(25)、式(30)、式(31)的自適應和差波束加權矢量對式(32)數據加權結果即為和差波束輸出值,由此可得到自適應單脈沖比

(33)

依照式(26)的約束準則設計的自適應波束可滿足在波束中心處的空域、時域單脈沖比皆為零且相互獨立,單脈沖鑒角率與靜態空域及時域單脈沖鑒角率一致,因此,估計方程簡化為

(34)

4 仿真實驗

本節仿真了嚴重非均勻環境下被檢測單元數據分布與其他距離單元不同的情況,以考察所提的無需參考數據的空時自適應單脈沖方法的適用性。實驗中的雷達系統參數為:采用沿平臺運動方向布置的N=16元均勻線陣,陣元間隔半波長d=0.5λ。雷達工作波長為0.23 m,載機速度為va=140 m/s,平臺高度為8 000 m,雷達最大作用距離Rmax=400 km,脈沖重復頻率為fr=2 434.8 Hz,CPI內有K=22個脈沖。

雷達工作環境如下:一個壓制性干擾位于方位120°,干噪比JNR=80 dB。某距離單元存在一個干擾目標,位于方位91°,其歸一化時間頻率為-0.22,JNR=80 dB。雜波存在功率非均勻的情況,即沿距離向雜波功率隨機分布,被檢測單元的雜噪比CNR=60 dB。以低速目標的空時參數估計為例給出性能分析,考慮波束中心位于(0,-0.2)。實驗中,本文提出的基于降維處理的直接數據域空時自適應單脈沖方法選擇的空時滑窗的維度為Nt=8,Kt=8;進而得到總的子快拍數P=135。

圖2給出了上述嚴重非均勻情況下單脈沖比的情況,橫/縱坐標均用全孔徑時靜態和波束的3 dB波束寬度歸一化。其中,“FDO”是指全維最優處理(full dimension optimum processing),即用被檢測單元的理論雜波、干擾協方差矩陣進行和、差波束形成所對應的空時二維自適應單脈沖比,這是一種理論的最優情況在實際中并不能得到;“FDA”是指全維自適應處理(full dimension adaptive processing),即按統計集平均的方法利用被檢測單元鄰近的多個距離單元的參考數據估計雜波、干擾協方差矩陣進行和、差波束形成獲得的空時二維自適應單脈沖比; “RDA” 是指降維自適應處理(reduced dimension optimum processing),即本文提出的無參考單元的方法;“FDQ” 和“RDQ”分別為用于比較的全維靜態(full dimension quiescent)和降維靜態(reduced dimension quiescent)的情況。由圖2可見,FDO和RDA方法的單脈沖比都與各自的靜態單脈沖比相似,因此這兩種方法的參數估計性能將比較好;而FDA方法偏離靜態單脈沖比的情況比較嚴重,這是由于嚴重非均勻環境下,與被檢測單元相鄰的快拍數據不具有同分布特性,引起了協方差矩陣估計誤差。

圖2 嚴重非均勻情況下單脈沖比曲線比較土Fig.2 Comparison of the monopulse ratios under seriously nonhomogeneous enviroments

圖3和圖4通過改變噪聲樣本各進行200次蒙特卡羅實驗,得到了均方根誤差(root mean square error,RMSE)隨目標位置及輸入信噪比變化的曲線,圖中的橫/縱坐標均用全孔徑時靜態和波束的3 dB波束寬度歸一化。RMSE反映了樣本偏離均值的程度(即標準差),其定義為

(35)

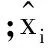
圖3 估計性能隨目標位置變化情況Fig.3 Comparison of the estimation performance versus varied positions of the target

在圖3所示的實驗中,SNR=0dB,目標位置在主瓣內變化。由圖可見,FDO方法具有最好的估計性能,這是由于一方面這種方法的單脈沖比線性特性保持的比較好(但由于波束窄,單脈沖比的線性區域比較小),另一方面這種方法用到理論雜波、干擾協方差矩陣,這就保證了能較好的實現自適應雜波抑制;而FDA方法的估計性能非常差,這是由于在上述兩方面此種方法都不能滿足;對比這兩種情況可知,雜波非均勻對全維方法的估計性能影響很大。而所提的RDA方法,其估計性能與理論情況FDO近似,明顯優于需要大量參考數據的FDA方法。

在圖4所示的實驗中,輸入信噪比的范圍為-10～20dB,感興趣的動目標位于方位88°,與載機之間相對速度對應的歸一化多普勒頻率為-0.177(相當于在空間向和時間向各偏離波束中心半個3dB波束寬度)。由圖可見,FDO方法和RDA方法的估計性能都隨輸入信噪比的提高而提高;同樣地,受非均勻環境的影響,FDA方法在任何輸入信噪比的情況下仍難以獲得較好的估計性能。從圖4和圖5可見,在嚴重非均勻情況下,本文提出的算法有更好的適用性。

為了檢驗在系統存在非理想因素下所提算法的性能,在不同陣元幅相誤差存在的情況下進行了下面的實驗。在圖5所示的實驗中,SNR=0dB,目標位置在主瓣內變化,陣元的幅相誤差分別為σa=σp=0.01、σa=σp=0.03和σa=σp=0.05。由圖可見,所提的RDA方法的估計性能明顯優于FDA方法,這說明所提方法對陣元幅相誤差更穩健。

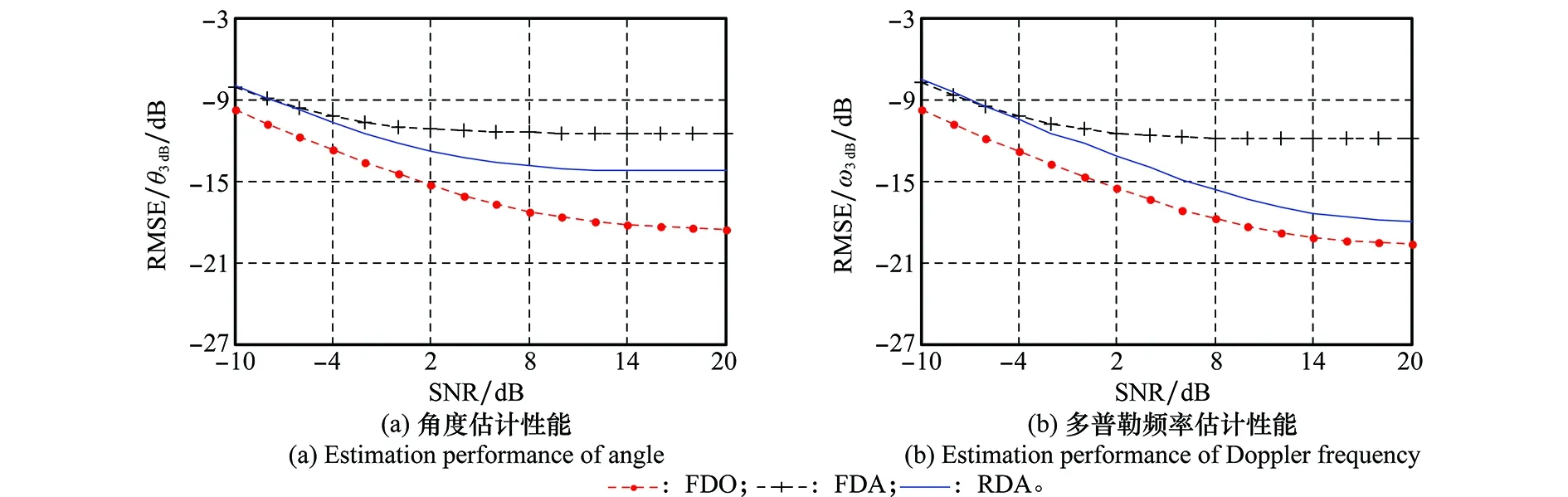
圖4 估計性能隨輸入SNR變化情況Fig.4 Comparison of the estimation performance versus different input SNR of the target

圖5 幅相誤差存在時估計性能隨目標位置變化情況Fig.5 Comparison of the estimation performance versus varied positions of the target under the presence of amplitude and phase error

5 結 論

本文針對嚴重非均勻環境下及孤立干擾存在的情況下機載雷達動目標參數估計問題進行了仔細的分析,并提出了一種新方法。在嚴重非均勻環境下,傳統單脈沖方法由于存在過多雜波剩余而無法得到準確估計,帶STAP處理器的單脈沖方法由于無法得到準確的雜波、干擾協方差矩陣亦僅有較差的估計精度。由于新方法無需利用參考單元數據,因此在非均勻環境適用性、運算存儲量、誤差穩健性等方面都具有明顯的優勢。

[1]NickelU.Overviewofgeneralizedmonopulseestimation[J].IEEE Trans.on Aerospace & Electronic Systems, 2006, 21(6):27-56.

[2]NickelU,ChaumetteE,LarzabalP.Estimationofextendedtargetusingthegeneralizedmonopulseestimator:extensiontoamixedtargetmodel[J]. IEEE Trans.on Aerospace & Electronic Systems, 2013, 49(3): 2084-2096.

[3]ChenL,ShengWX,HanYB,etal.Animprovedadaptivemonopulsealgorithmbasedonsubspaceprojection[J]. Journal of Electronics & Information Technology, 2013, 35(9): 2100-2107.(陳亮,盛衛星,韓玉兵,等. 一種改進子空間投影自適應單脈沖算法[J].電子與信息學報, 2013, 35(9): 2100-2107.)

[4]LiRF,RaoC,DaiLY,etal.Algorithmforconstrainedadaptivesum-ddifferencemonopulseamongsub-arrays[J]. Journal of Huazhong University of Science & Technology (Natural Science Edition), 2013, 41(9):6-10.(李榮鋒,饒燦,戴凌燕,等. 子陣間約束自適應和差單脈沖測角算法[J]. 華中科技大學學報(自然科學版), 2013, 41(9): 6-10.)

[5]ZhangZC,TaiXJ,MengQC,etal.Analysisontheeffectofmain/sidelobejammingonmonopulseangleestimate[J]. Radar Science and Technology,2012,10(2):207-211,216.(張忠傳,邰新軍,孟慶昌,等.主/旁瓣干擾對單脈沖測角的影響分析[J].雷達科學與技術,2012, 10(2): 207-211,216.)

[6]ChenCZ,WuJX,WangT,etal.Monopulseangleestimationwithadaptivearraybasedonmonopulseresponsecurvefitting[J].Systems Engineering and Electronics, 2013, 35(7): 1403-1408.(陳成增,吳建新,等.基于鑒角曲線擬合的自適應單脈沖測角方法[J].系統工程與電子技術,2013,35(7):1403-1408.)

[7]MelvinWL.ASTAPoverview[J].IEEE Trans.on Aerospace & Electronic Systems,2004,19(1):19-35.

[8]WangL,SuZG,WuRB.Linear-constraintbasedspace-timeadaptivemonopulseprocessingtechnique[J]. Journal of Electronics and Information Technology, 2010, 32(10): 2501-2505.(王璐,蘇志剛,吳仁彪. 基于線性約束的空時自適應單脈沖技術[J]. 電子與信息學報,2010, 32(10):2501-2505.)

[9]ChenG,XieWC,WangYL.Space-timeadaptivemonopulseangleestimationapproachforairborneradarbasedonspace-timejointconstraint[J]. Acta Electronica Sinica, 2015, 43(3):489-495.(陳功,謝文沖,王永良. 基于空時聯合約束的機載雷達STAP單脈沖角度估計方法[J]. 電子學報,2015,43(3):489-495.)

[10]WuRB,SuZG,WangL.Space-timeadaptivemonopulseproces-singforairborneradarinnon-homogeneousenvironments[J]. AEU International Journal of Electronics and Communications, 2011, 65(5): 258-264.

[11]XieW,ChenJ,WangYL.StudyonSTAPinnon-homogeneousclutterenvironment[C]∥IEEE Aerospace Conference, 2008: 1-6.

[12]TsakalidesP,NikiasCL.Robustspace-timeadaptiveprocessing(STAP)innon-Gaussianclutterenvironments[J]. IEE Proceedings, Radar, Sonar and Navigation, 1999, 146(2): 84-93.

[13]RabideauDJ,SteinhardtAO.Improvedadaptivecluttercancellationthroughdata-adaptivetraining[J]. IEEE Trans.on Aerospace & Electronic Systems, 1999, 35, 879-891.

[14]MelvinW,WicksMC.Improvedpracticalspace-timeadaptiveradar[C]∥Proc.of the National Radar Conference,1997:48-53.

[15]CristalliniD,BurgerW.ArobustdirectdatadomainapproachforSTAP[J]. IEEE Trans.on Signal Processing, 2012, 60(3): 1283-1294.

[16]LapierreF,VerlyJ,DroogenbroeckM.NewsolutionstotheproblemofrangedependenceinbistaticSTAPradars[C]∥Proc.of the IEEE Radar Conference, 2003:452-459.

[17]MichelsJ,HmedB,RangaswamyM.EvaluationofthenormalizedparametricadaptivematchedfilterSTAPtestinairborneradarclutter[C]∥Proc.of the IEEE Radar Conference, 2000: 769-774.

[18]GerlachK,PiccioloM.Airborne/spacebasedradarSTAPusingastructuredcovariancematrix[J]. IEEE Trans.on Aerospace & Electronic Systems, 2003, 39(1):269-281.

[19]GiniF.Knowledge-basedsystemsforadaptiveradar[J]. IEEE Signal Processing Magazine, 2006: 14-17.

[20]SuZG,ZhangKX,PengYN,etal.Rank-deficientAPESfilterforcomplexspectralestimation[C]∥Proc.of the IEEE Radar Conference, 2008: 26-30.

Direct data domain space-time adaptive monopulse method

WANG Lu, WU Ren-biao

(TianjinKeyLaboratoryforAdvancedSignalProcessing,CivilAviationUniversityofChina,Tianjin300300,China)

Space-time adaptive processing (STAP) for airborne radar combined with the monopulse technique can be used for estimating the spatial and temporal parameters of moving targets. However, in non-homogeneous environments, the clutter covariance matrix is difficult estimated accurately due to the amount of identically distributed training data is limited. As a result, the performance of optimum STAP and its modified versions dramatically decrease, especially those methods are failed. Additionally, in this case the effectively target detection and parameters estimation cannot be realized. A novel method is proposed for parameters adaptive estimation via no secondary data. This method calculates the covariance matrix by applying the amplitude and phase estimation (APES) filter in the primary data firstly. Then, by combining STAP technique with the monopulse theory, the ground clutter is suppressed and the estimation of angle and Doppler frequency is obtained. Simulation results show that the proposed method has the capability of adaptive clutter suppression and can achieve accurate parameter estimation performance compared with the conventional monopulse method. This method is outstanding in severe non-homogeneous environments, because it does not need any secondary data.

airborne radar; space-time adaptive processing (STAP); monopulse technique; non-homogeneous clutter

2015-12-22；

2016-06-23；網絡優先出版日期：2016-07-18。

國家自然科學基金(61231017,U1333106)；中央高校基本科研業務費(3122016D004)資助課題

TN 957.51

A

10.3969/j.issn.1001-506X.2016.12.09

王 璐(1984-),女,講師,碩士,主要研究方向為陣列信號處理、自適應天線技術。

E-mail:luwang@cauc.edu.cn

吳仁彪(1966-),男,教授,博士,主要研究方向為自適應信號處理、譜估計方法。

E-mail:rbwu@cauc.edu.cn

網絡優先出版地址：http://www.cnki.net/kcms/detail/11.2422.TN.20160718.1040.008.html