基于半鞅過程的中國股市隨機波動、跳躍和微觀結構噪聲統計特征研究

劉志東，嚴 冠

(中央財經大學管理科學與工程學院，北京 100081 )

?

基于半鞅過程的中國股市隨機波動、跳躍和微觀結構噪聲統計特征研究

劉志東，嚴 冠

(中央財經大學管理科學與工程學院，北京 100081 )

本文基于半鞅過程和非參數統計推斷方法，利用已實現冪變差的漸進統計特性，構造檢驗統計量，在統一的分析框架下，對金融資產價格中隨機波動、跳躍和微觀結構噪聲等問題進行全面系統的研究。并根據上海證券交易所不同行業的股票，上證50 股票指數及其成分股的高頻數據進行實證研究。結果表明，我國A 股市場中，噪音交易顯著；約43%的風險來源于資產收益過程的隨機波動風險，可用股票期權交易對沖；不同來源風險的重要性程度依次為：隨機波動的風險、系統性跳躍風險以及異質性跳躍風險；流動性越好的股票越顯示出跳躍、尤其是無限小跳的證據。

高頻數據；半鞅過程；跳躍；微觀結構噪聲；流動性

1 引言

由于數學上易處理性和滿足無套利要求條件，半鞅(Semimartingales)作為現代資產定價理論基礎，在連續時間金融計量中已得到了廣泛應用。半鞅可以分解為漂移項(drift)、連續局部鞅(Continuous Local Martingale)和不連續Levy 跳躍項 (Discontinuous Levy Jump)。Levy 跳躍項又可以分解成小跳躍(Small Jump) 和大跳躍(Big Jump)。最初連續時間金融計量方法僅采用低頻數據(Low Frequency Data)估計模型。隨著計算機技術與通訊技術的發展進步，高頻率金融數據的采集和存儲變得越來越容易，利用離散高頻數據估計連續時間計量模型成為金融計量研究熱點。已實現方差(Realized Variance)成為估計價格過程二次變差(Quadratic Variation) 和積分波動性(Integrated Volatility)的有效方法。然而，在高頻數據中，由于微觀結構噪音影響，已實現方差在兩方面受到限制。第一，已實現方差對高頻數據固有的市場微觀結構噪音非常敏感，結果會降低估計量的一致性。第二，已實現方差是擴散變差和跳躍變差(Diffusive and Jump Variation)之和的全變差估計量，不能區分擴散變差和跳躍變差。而把波動性和跳躍區分開對衍生品定價、風險度量與管理以及資產配置至關重要。為此，很多研究中從兩個不同的角度展開。其中一個是關于跳躍穩健的已實現方差測量方法研究。這主要包括： Barndorff-Nielsen 和Shephard[1]提出的雙冪變差(Bi-power Variation)，以及Jacod[2]，Mancini[3-4]提出的閥值估計量(Threshold Estimators)。另一個是關于噪音穩健的已實現方差度量方法研究。這些主要包括Zhang Lan[5]，Zhang Lan等[6]的二次抽樣方法，Barndorff-Nielsen 等[7]，Zhou Bin[8]提出的基于核的自協方差調整方法，Jacod 等[9]，Podolskij 和Vetter[10]提出的前置平均方法，Andersen 等[11]，Bandi 和Russell[12]提出的稀疏采樣方法，Andersen 等[11]，Bollen 和Inder[13]，Hansen，Large和Lunde[14]的前置過濾方法，Corsi 等[15]基于模型的改正方法，Fan Jianqing和Wang Yazhen[16]等基于小波的方法等。然而，這些研究幾乎只對離散抽樣半鞅中的連續項(積分波動性)進行研究，很少同時考慮 微觀結構噪音和跳躍，導致跳躍穩健的已實現方差測度通常對噪音不穩健，噪音穩健的已實現方差測度通常對跳躍不穩健。同時，這些研究都假設不同時間的噪音相互獨立，與資產價格不具有相關性。這與現實情況不符。

盡管金融資產價格跳躍及其重要性已經得到普遍承認，但只有最近的計量經濟模型能對跳躍過程進行嚴密的分析。一些高頻計量文獻開始超出波動性，對離散抽樣半鞅中的不連續或跳躍項進行研究。這包括： 關于跳躍檢測統計量的研究，如Barndorff-Nielsen 和Shephard[17]的BN-S 檢驗統計量，Jiang 和Oomen[18]的J-O 檢驗統計量，Lee 和Mykland[19]的L-M 統計量，以及 A.t-Sahalia 與Jacod[20]的A-J 檢驗統計量等。然而，實證研究發現這些方法只能識別有限活動跳躍，很難識別無限活動跳躍。同時，這些方法幾乎沒有考慮觀測價格過程中微觀結構噪音的存在。結果導致這些統計檢驗方法可能對微觀結構噪音不穩健，出現對跳躍是否發生的錯誤識別。目前在跳躍檢驗統計量中直接考慮噪音的影響的研究還很少。

國內關于金融資產價格跳躍問題也從參數方法和非參方法兩個方向著手。參數方法方面，胡素華等[21]，任楓等[22]分別運用MCMC 對非對稱雙指數跳躍擴散模型進行估計，驗證MCMC 方法對處理非對稱雙指數跳躍擴散模型這類含有隱含變量的多參數模型估計的有效性。馬宇超等[23]根據中國股價波動規律，提出一個帶均值回復項的跳躍擴散模型，即在漂移項中加入均值回復過程和跳躍因素，并以上證指數數據為樣本，給出模型的參數估計方法。曹宏鐸等[24]則在Merton 提出的跳躍擴散模型基礎上對Poisson 計數過程以及跳躍幅度都施加冪律性質，以更為精準地描述股票價格的走勢，并驗證了收益率的厚尾分布以及波動積聚性等特點。國內利用高頻數據檢驗跳躍的非參的方法主要通過沿用或改進國外的非參檢驗方法對我國股票市場中的跳躍行為進行實證檢驗，進而驗證跳躍與股票市場波動率之間的關系。如：陳國進和王占海[25]利用滬深300 指數一分鐘高頻數據分離處理已實現波動率中的連續性波動和跳躍性波動成分，并檢驗兩種波動率之間的同期以及跨期相關性。楊科，陳浪南[26]分別運用修正的已實現門閥的多次冪變差以及自回歸條件持續期模型、風險模型以及擴展的風險模型實證分析了中國股市的跳躍特征，包括持續期的長記憶性及周日歷效應，幅度、強度分布的時變性以及對高頻波動率的貢獻。唐勇，張伯新[27]結合A-J 統計量對跳躍的方差進行建模分離跳躍因素，并檢驗我國股市跳躍的收益率、方差及方向等特征，進而判斷跳躍方差對總方差的貢獻率。非參方法應用的另一角度，則著重探討跳躍的發生與信息融入程度之間的關系，如：歐麗莎等[28]利用基于BN-S 方法的已實現波動率測度構造跳躍統計量，證實我國股票市場價格跳躍行為存在普遍性，并且發現單只股票的跳躍行為更多地受到個體異質信息的影響，單只股票的共同跳躍現象多被噪聲和異質跳躍所覆蓋。國內同時考慮跳躍行為及市場微觀結構噪聲的研究少之又少，馬丹和尹優平[29]提出在將動態門限方法引入預平均收益率的研究框架下，進而在跳躍和噪聲同時存在的條件下對波動率進行一致、無偏的估計。唐勇，寇貴明[30]分離出我國股票市場上證綜指高頻序列中的噪聲成分和跳躍成分，并計算其流動性水平，對三者關系進行實證檢驗，結果顯示噪聲因素和跳躍成分之間存在顯著正相關關系，而流動性水平則與兩者都呈負相關關系。

目前國內外研究大多從統計學角度單獨研究隨機波動和跳躍問題的某一方面。由于各種方法的適用條件不一樣，所得的結論也不太一致。Ait-Sahalia 和Jacod[20，31-36]通過構建已實現冪變差(Realized power Variations)統計量，通過變化冪參數、截斷水平、抽樣頻率，來確定收益過程是否存在跳躍項和連續項，跳躍的類型，以及跳躍和連續項的相對幅度等。該方法為在一體化框架下，系統研究跳躍、隨機波動率和微觀結構噪聲等提供了新的思路和方法。因此，利用金融高頻數據全面系統研究微觀結構噪音、波動性、跳躍，能夠使我們更為準確的對波動率度量和跳躍檢測，能夠分清市場風險類型，從而更為有力的對不同類型風險進行防范與管理。

本文結構如下：第一部分引言。第二部分構建本文的理論框架，第三部分將有統一框架的方法論應用于中國A 股市場的現實數據時，進行實證分析。第四部分為本文的結論。

2 金融資產價格的半鞅過程

本文假設對數價格Xt服從Ito半鞅，表示為：

(1)

(2)

當跳躍是有限活動的跳躍時，或者說它們是可加的

∑s≤t|ΔXs|<∞，s

(3)

時間的跳的大小為：

ΔXs=Xs-Xs-

(4)

重寫式有：

(5)

(6)

這與實際的不可觀測的跳的大小ΔXs有所不同。

3 測度工具與檢驗統計量

本文基本的方法論是構造這些增量的已實現冪變差，定義為：

(7)

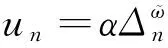
(8)

顯然它們之間的關系為：

U(p,un,Δn)=B(p,∞，Δn)-B(p,un,Δn)

(9)

如果是計數增量(或跳躍)的個數，則取冪指數p=0：

(10)

對于選擇不同的冪指數p，截斷率nu以及抽樣頻率Δn這三個控制變量，B 和U 的漸進性質有所不同，使我們能夠靈活地分離我們關注的部分。第一個控制變量是冪指數，冪指數的作用在于分離出或保留下連續部分或者跳躍部分。第二個控制變量是截斷率。根據公式，當抽樣頻率上升，截斷率逐漸變小，而因為大跳的規模是一定的，在漸進的過程中，截斷率總會小于大跳，這樣就在計算冪變差B 的時候忽略掉了這些部分。第三個控制變量是抽樣頻率。不同的頻率抽樣可以辨別出三種不同的情形。通常是采用最高頻率Δn和某個略低的頻率kΔn(k≥2)下兩個B 的比值來確認B 的極限情況。

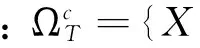
3.1 跳躍存在性的檢驗統計量

首先引入兩個過程，它們衡量了X 的波動性，又取決于整個不可觀測的路徑。

(11)

( 12 )

其中mp表示標準正態變量的p階絕對矩。由上述性質，我們可以令p>2，比較在兩種不同抽樣頻率下的B，有如下的檢驗統計量SJ：

(13)

并有如下性質：

(14)

存在跳時，B 是收斂到一個有限的極限的，所以比值趨于1；若無跳，B 趨于0，這時比值收斂于一個大于1 的極限，這個極限值取決于B 趨于0 的速率。

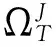
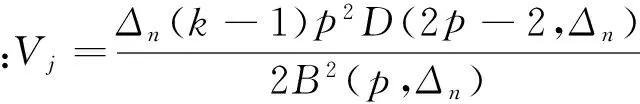
3.2 跳躍類型的檢驗統計量

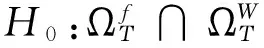
(15)

與上一個統計量的不同之處在于截斷水平。同樣，p>2 是為了放大跳的部分，截斷是為了消除掉大跳，由于大跳的大小是有限的，獨立于Δn，所以在漸進過程中，截斷水平un=αΔ?n總會在某時過濾掉所有大跳，所以如果只有大跳的話，統計量的極限就會類似于在跳的存在性檢驗中沒有跳存在的情況。但是，如果存在無限小跳的話，截斷水平不能將它們全部過濾出去，所以兩種抽樣頻率的B 都會表現為小于截斷水平的跳的p 次冪的和，所以兩個B 都以相同的速度趨于0，因此比值為1[35]。

(16)

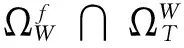
對于隨機集合IT={p≥0：J(p)<∞}，有[βT,∞ )或(βT，∞)的形式，其中βT(ω) ∈[0, 2]，而總有2∈IT。可以證明IT的下界βT(ω )是T 時刻路徑t→Xt(ω) 跳活動的可用測度。我們稱βT為一般性BG指數(Blumenthal-Getoor index,)，或者稱為跳活動程度。我們假設(2)中的Levy 測度v有如下形式[33]：

(17)

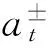
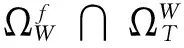
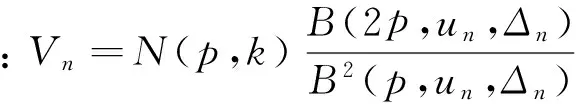
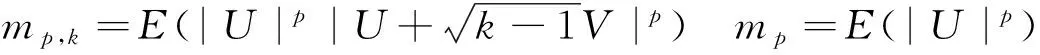
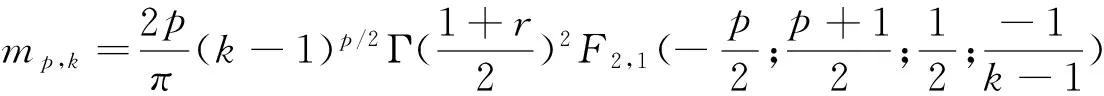
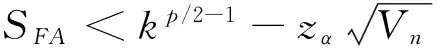
3.3 布朗運動存在性的檢驗統計量

我們令p小于2，以放大冪變差中布朗運動的部分，選擇整數k≥2， p<2，有如下檢驗統計量[34]：

(18)

有極限：

(19)

第一個收斂性質不需要關于跳躍的額外假設，而第二個收斂性質假設需要滿足(17)。

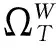
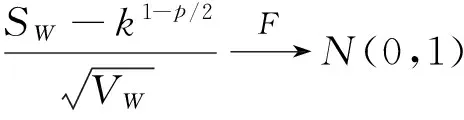
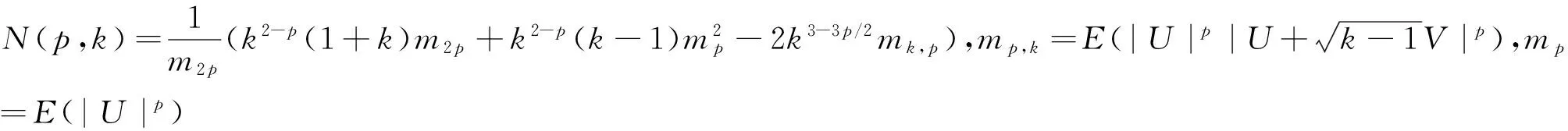
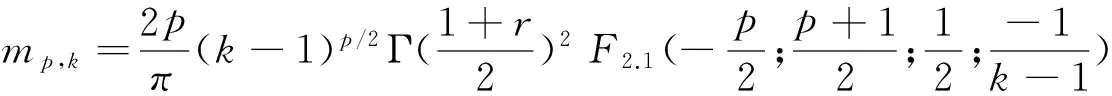
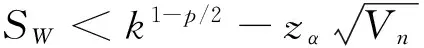
3.4 跳躍項和擴散項的相對大小的統計量

p=2時，各部分是漸進同階的。通過截斷，我們可以將二次變差分為連續和跳躍兩部分：

(20)

3.5 跳躍活動程度的估計

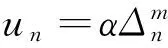
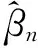
(21)

第二種方法是通過變化抽樣頻率，以兩種時間頻率Δn和2Δn抽樣，得到如下估計量：

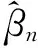
3.6 市場微觀結構噪聲影響下各種統計量的極限

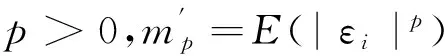
(2) SFA的極限：

4 實證研究

4.1 數據選擇

本文從上海證券交易所的A 股中選擇樣本，利用前述的方法分析中國股票跳躍、隨機波動和微觀結構噪聲的統計特征。首先，從各行業等量抽取具有代表性的樣本，根據統計量得出相應的各支股票的結論后，比較不同行業股票收益的統計特征。其次，以上證50(代碼：000016)這只股票指數為例，分別分析單一的股票指數以及組成它的樣本股票的性質，得出有關股票分散化的結論。最后，以組成上證50 的50 只股票為樣本，依據流動性分組，比較流動性不同的股票的收益特征。

(1)第一組實證研究是為了比較不同行業股票收益的統計特征，并總結跳躍行為的橫截面特征，因此數據樣本選擇依據上證行業指數的分類方法，分為能源、材料、工業、可選消費、消費、醫藥、金融、信息、電信、公用這十個行業。對于每支行業指數，在其成分股之中，再選擇2012 年12 月31 日流通股市值排名前五的，作為具有代表性的公司組成行業樣本； 再分取2012 年四個季度組成縱向樣本，一共五十支樣本，但由于大唐電信缺失三個月的數據，因此剩余四十九支樣本。原始數據是上海證券交易所2012 年A 股的逐筆數據，包括日期、時間、報價、交易量、交易額、方向、排名前五的買入價和排名前五的賣出價。本文基于五秒抽樣將數據標準化，即，將每天4 個交易小時，分成共2882 個抽樣點，若抽樣點上有對應的交易價格，則取入，若沒有剛好對應的，則取離此抽樣點最近的交易價格，若有交易價格的兩個時間點距抽樣點的距離一樣，則取它們的平均值。五秒的頻率是因為抽樣過于稀疏可能導致波動率的集聚被誤認為跳躍。另外，在計算對數收益之后，去掉每一天第一個收益，即消除隔夜收益。

(2)第二組實證研究是為了研究分散化對跳躍特征的影響，因此需要選定一支股票指數，選擇上證50 是因為樣本容量的近似使其結果可以與第一組實驗相對照。上證50(代碼：000016)這支股票指數在2012 年12 月31 日時的成分股見附錄F。上證50 指數是根據科學客觀的方法，挑選上海證券市場規模大、流動性好的最具代表性的50 只股票組成樣本股，以便綜合反映上海證券市場最具市場影響力的一批龍頭企業的整體狀況。使用的數據性質同上，并使用了相同的預處理方式。

(3)第三組實證研究是為了比較不同流動性股票的收益特征，為了前后研究結果的可比性，仍然使用上證50 的成分股。以平均交易間隔時間作為各支股票流動性的代表，將上證50 的五十只成分股按照流動性平均分成五組，每組十支股票，取第一、三、五組作為高、中、低流動性的代表。

4.2 行業股票實證結果與經濟含義

(1)跳躍是否存在

SJ實證值的詳細結果如表1 所示，計算是依據每個行業的五支股票在四個季度的數據，p 以0.25 的增量從3 取到6，時間間隔從5 秒取到2 分鐘，分別是5，15，30，60，90，120 秒，k 取2 和3。在表1 中，SJ的數值通過如下的規則確定：若顯示J S 有明顯的極限，并且極限與其中位數所在的判定區域一致，則取其中位數，例如大秦鐵路的SJ的中位數為0.7303，SJ極限也在<1 的范圍內；若顯示SJ有明顯的極限，但其中位數與此極限所在的區域不一致，則使用極限值所在的區域，例如東方通信SJ的中位數是1.0205，顯然與<1 的情況不一致。若J S 存在一個以上極限的，則標記為“-”，例如烽火通信；若SJ在觀測范圍內沒有極限，則標記為N，例如三一重工。

從表1 可以看出，若利用本文的統計檢驗方法，我們認為，樣本中金融類的中國平安、招商銀行，信息類的用友軟件，可選消費類的青島海爾和電信類的中天科技這五支股票的資產收益序列中是存在跳的。5/49 的跳躍存在比例與Pierre 等所得出的10% 的實證結果相吻合，但Pierre 等側重時間序列比例，而本文是橫截面的比例。

存在跳的兩家金融類企業屬于樣本中市值靠后的，但用平均交易間隔時間來衡量，它們的流動性是最好的，同時，這兩家企業的股權集中程度低于另外三家企業；在可選消費類中，只有青島海爾的統計量指示有跳的存在，其他四支股票都由噪音主導，青島海爾也是這五只樣本中，股權集中程度最小的；在電信行業中，存在跳的中天科技是樣本中股權集中程度最小的。各行業的證據均表明，存在跳而非被噪聲主導證明其股價能夠較為及時理性地反映各種信息，因而產生了跳躍行為，而不是由于噪音交易者非理性的交易行為而掩蓋了價格對信息的反應。

(2)跳躍是有限活動跳躍還是無限活動

由于存在跳的資產才能夠區分跳是否無限活動，即是否存在無限小跳，那么觀察這五支樣本的SFA，極限均在1 以下，說明噪音顯著。其中，中國平安顯示出一些無限小跳存在的特征，對比可知，中國平安是這五只存在跳的股票中流動性最強、股權集中程度最低的。從經濟意義上來說，模型中的小跳部分代表的是各類微觀市場結構，例如由于市場吸收大筆交易帶來的價格變化的風險，由于中國平安的股權較為分散，投資者異質性程度高，交易頻繁，可能在極短時間內產生由于微觀市場結構帶來的價格波動。

(3)布朗運動是否在性

為了驗證檢驗結果對參數選擇的穩健性，選取不同的p和k值進行檢驗，表2 給出了檢驗結果。可以看出，單個SW的拒絕域并不能區分不拒絕存在布朗運動的原假設之后的其他情況，因此，我們需要大量的SW值來確認其分布的極限，進而區分存在布朗運動以及噪音主導的情形。在SW的計算中，p取1到1.75，α取5 到10 個標準差，Δn從5 秒到2 分鐘，k 取2 和3. SW在1 到1.75 間，被認為是存在布朗運動的指示，例如包鋼稀土。大于1.75則是顯示噪音主導，如紫金礦業。有多個極限則表明是由近似誤差主導，例如中國建筑。各支樣本股票的SW的具體值見表3。A 股中一半的資產收益過程是存在布朗運動的，近似誤差主導的資產收益可能與中國股市只能整手(100 股)買入有關，這一交易機制限制了一部分流動性，同時，間接地影響了股價的最小變化單位。分行業來看，電信行業是基本存在布朗運動的，工業則主要由噪音主導，公用行業由近似誤差主導，原材料行業、消費行業和可選消費行業大部分存在布朗運動，信息行業和醫藥行業絕大部分存在布朗運動，金融地產和能源的行業特征不明顯。

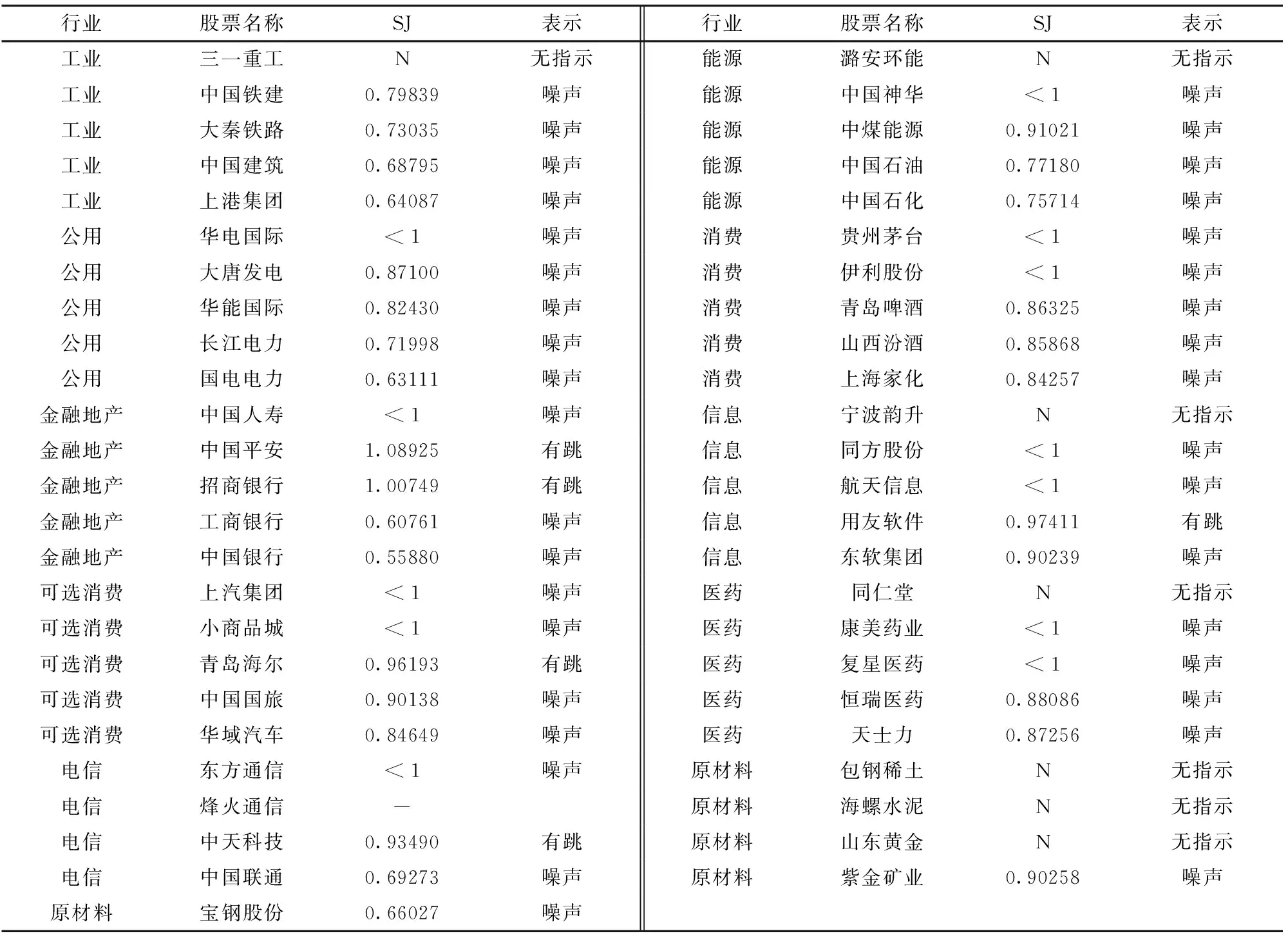
表1 跳躍檢驗統計量的取值及其表示

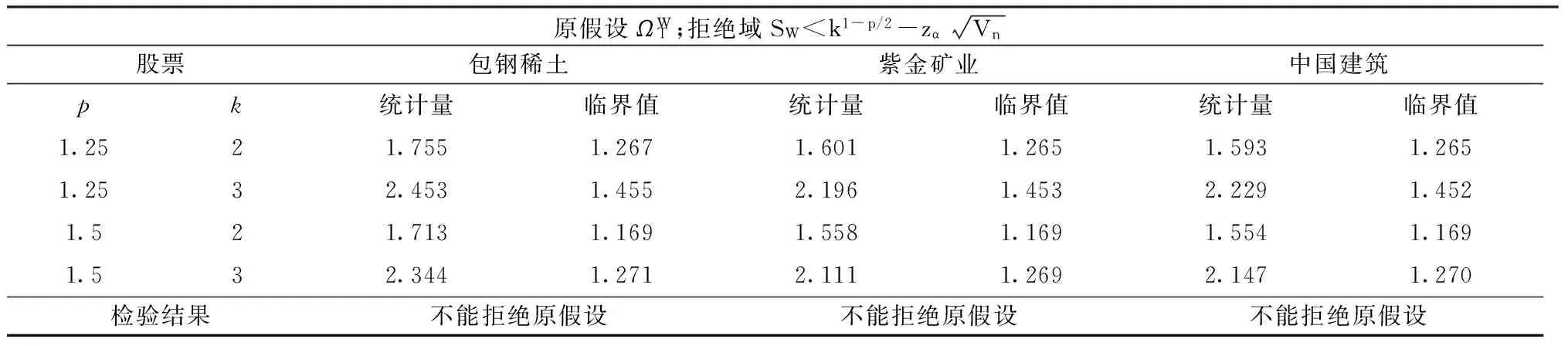
表2 布朗運動存在性的檢驗結果

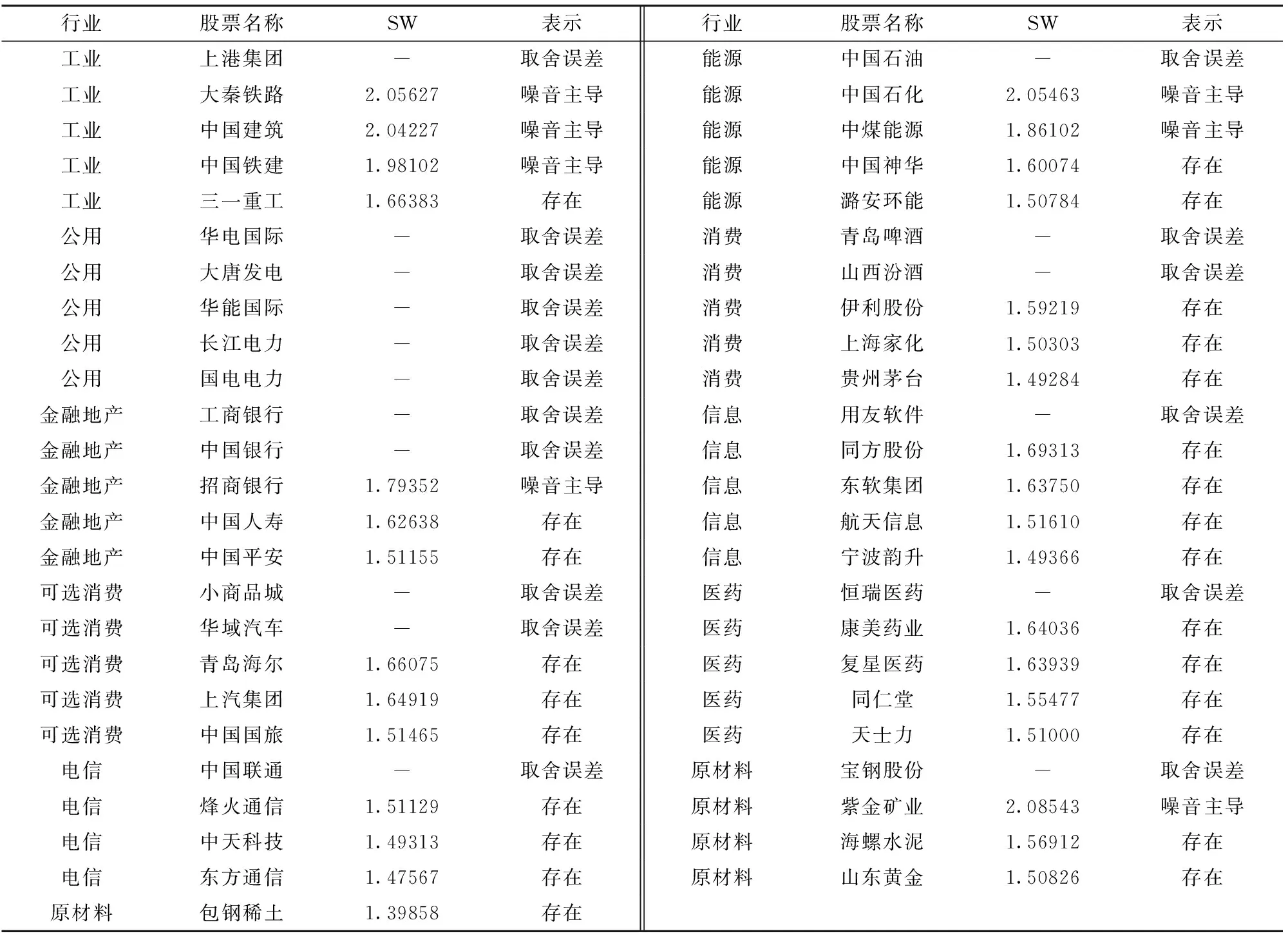
表3 布朗運動檢驗統計量的取值及其表示

表4 是否存在布朗運動的檢驗結果

(4)二次變差的相對大小

本文中QV 的計算，α取2 到5 個標準差，Δn從5秒到2分鐘。詳細結果見表5。根據A?t-Sahalia. et al (2012)的研究，QVSplit 越大，代表流動性越好。以平均交易間隔時間為流動性的度量，可以看出，它和QVSplit 有近似的負相關關系。因此各行業的布朗運動占比，近似于總體流動性大小的排序是：金融地產，工業，電信，能源，原材料，信息，醫藥，可選消費，消費。總體來說，還是有近一半的風險來源于資產收益模型的連續部分，即代表資產的隨機波動風險，可用微分方法對沖，可見近期國家開放股票期權交易有助于投資者規避風險，增強金融市場的穩定性。

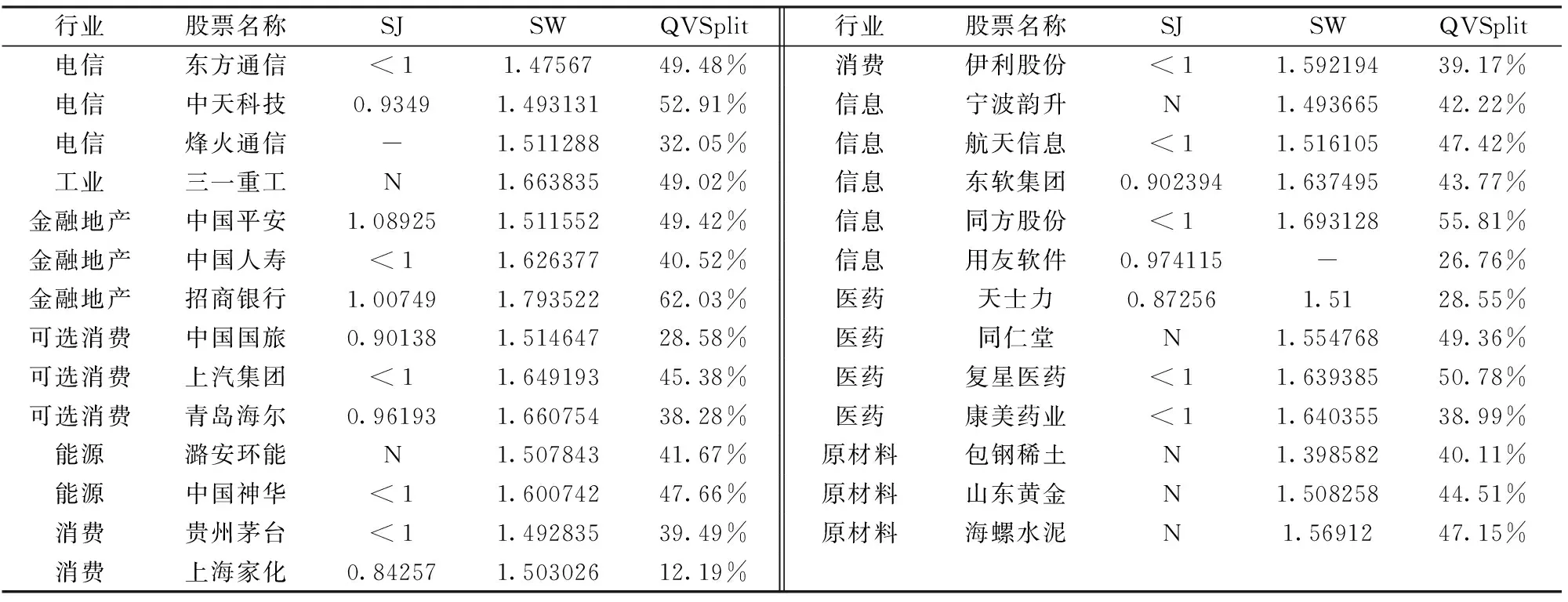
表5 布朗運動占比的統計結果

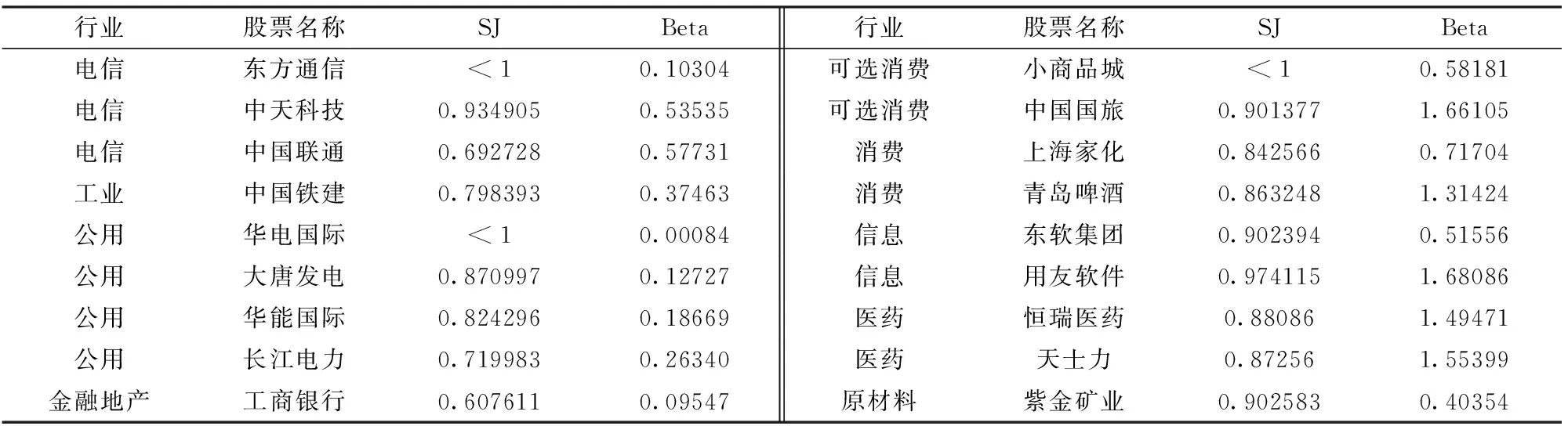
表6 跳活動程度的估計結果

(5)跳活動程度的估計

對于跳活動系數的計算，α取5 到10 個標準差，Δn從5 秒到10 秒。根據上述理論，跳活動系數在0到2 之間才是有意義的，同時，如果J S 明確顯示其不存在跳，則此系數同樣沒有意義，排除這些無意義的估計值，得到的結果詳見表6。按照β的定義，若越接近于0，則跳的活動程度越接近于復合泊松過程，即存在有限大跳，若越接近于2，則跳的活動程度越接近布朗運動，即存在無限小跳。

4.3 股票指數和其成分股的實證結果與經濟含義

股票指數顯示了分散投資的益處，例如，若有兩只股票同時發生跳躍行為，規模相同，方向相反，此時股票指數的收益不會發生變化，表明這是一種可以通過分散投資規避的風險，然而將這兩只股票納入成分股的樣本當中時，則算作是有兩次跳躍行為發生。所以市場指數出現跳的行為，一般被認為是系統性風險的代表，而個股的跳行為，則是代表異質性風險，由此可以提出假說，即股票指數會顯示出比其成分股更少的跳躍行為的特征，并且趨向于有限活動而不是無限活動。本文通過數據來驗證上述假說。

(1)跳的存在性

從實證計算結果可以明顯看出，股票指數沒有顯示出有跳的存在，而組成它的單只股票統計量的極限值為1，表明有跳。這驗證了之前的假說，表明單只股票的跳行為代表的是異質性風險，而股票指數則代表了系統性風險，2012 年沒有太多令市場迅速并大幅度反應的系統性事件。這也驗證了Merton[37]的假設，他認為跳躍部分是非系統性的，可被分散的。Pierre 等的研究結果也表明沒有同時影響所有股票的共跳，間接證明了跳躍風險是可分散的。這對衍生品定價以及風險管理有重要的現實意義。

(2)跳的無限活動

與前一類對于各行業股票的分析類似，盡管成分股存在跳，但是其無限小跳或有限大跳的統計量卻只顯示出資產收益的過程被噪音主導，無法得出相關的結論。

(3)布朗運動的存在性

顯然，兩種情況下的統計量都顯示出存在布朗運動的性質。而成分股的統計量更趨向于顯示噪音主導，可見個股面臨更多由噪音交易者帶來的股價異常波動所表示的風險。

(4)二次變差的相對大小

上證50 的指數收益過程中，布朗運動貢獻的二次變差的百分比大約是70%，而其成分股表現出的資產收益過程中，布朗運動貢獻的二次變差的百分比則是55%左右，二次變差中歸因于跳躍部分的比例在指數的成分股中較高。這驗證了有關跳存在性的結論。據此，還可以分析出異質性跳躍、系統性跳躍以及布朗運動對二次變差的貢獻率，系統性跳躍占23.57%的二次變差，異質性跳躍占了21.43%，連續部分則占了55%。這再次驗證了將跳躍部分作為資產收益方差來源的重要性。

4.4 不同流動性的特征比較

由實證計算結果可以看出，流動性高的股票呈現出指示存在跳躍的統計量極限值，而流動性弱的股票則因為噪音主導無法顯示。Pierre 等在應用2006 年至2008 年道瓊斯股票所做的實證中，證明了90%的跳躍都是被過度檢出的，其余真實的跳躍與新聞、公告以及事件有關，大多數新聞不會導致跳躍，而只是產生波動率異象的市場反應。若跳躍的發生是由信息或信息披露前的流動性變化導致的，則跳躍是流動性好的股票及時消化和反映了這一信息的表征，而流動性差的股票則因為買賣價差大、交易者信念異質程度高，噪音顯著。

流動性高的股票不但顯示存在跳，而且不同于其他兩類圖示仍然被噪音影響的情況，無限小跳的存在性也可以被看出。Christensen 等最新基于超高頻數據或逐筆交易數據也發現，以往通過設定最佳的抽樣頻率來消除或減少微觀結構噪聲的非參數跳躍檢驗方法可能忽略掉微觀結構噪聲隱含的重要信息，過高估計了金融高頻時間序列中跳躍發生概率，而檢測到跳躍有可能是由于市場摩擦引起的微觀結構噪聲。由此可見，我國漲跌停制度、整手買入等限制性的交易制度等可能成為小跳產生的原因。

三者都顯示布朗運動的存在性，但是流動性越高，這種極限的特征越明顯；流動性高的股票顯示出比其他兩類更低的布朗運動占比，再次驗證了流動性高的股票收益過程中存在跳，這在一個側面反映出流動性高的股票反應信息的即時性。

5 結語

本文中所敘述的方法可以將資產價格過程分解成它的組成部分，并分析它們之間的相對大小以及一些更加精細化的特征。這種方法為與資產收益過程假設相關的問題提供了一個統一的框架和方法論；作為一種非參數方法也避免了模型誤設風險；考慮到了市場微觀結構噪聲的兩個來源，將它們的影響納入到了統計量性質的考慮之中。

但是另一方面，如果單獨考慮本文中所提出的五個問題，那么本文提出的統計量不一定是回答特定的某個問題最好的方法，同時，雖然我們推斷出了當噪音主導時，統計量的漸進性質，但是并沒有一個在噪聲存在的情況下依舊穩健的統計量。

在這個統一的框架下，本文對A 股市場中資產收益過程的跳躍行為進行了相關研究，得出如下主要的結論：

在依據行業的分析中，可以推斷出(1)我國A 股市場中噪音交易者較多，導致資產收益的序列并非呈現出一般意義上跳-擴散過程的狀態。例如，在使用中國證券市場上的高頻數據進行研究時，并沒有很多顯示出明顯存在跳的情況。同樣，對于是無限小跳還是有限大跳的區分，大部分情況下，也因為噪音顯著，并不明顯。(2)對于存在跳躍行為的股票來說，它們基本上是各行業內流動性好、股權集中程度低的。(3) 布朗運動的確廣泛存在于各支股票的收益序列中，大約有一半的樣本股票通過統計量顯示出了其含有布朗運動的性質。另有近35%的股票顯示出近似誤差主導的性質，可能是由于交易制度的原因，如只能整手買入股票的限制。(4)布朗運動對二次變差的貢獻約為42.88%，各行業之間有所區分。

在對股票指數及成分股的分析中，我們看到雖然成分股的統計量顯示出存在跳的極限值，但是股票指數卻沒有顯示其過程中有跳，這表明有一部分跳的風險是異質性的，可以被分散。進而，我們得出了貢獻二次變差的三個部分的近似占比，系統性跳躍占23.57% 的二次變差，異質性跳躍占了21.43%，連續部分則占了55%，這些占比大致反映了A 股市場中不同來源風險的相對大小，可以作為建模的依據。這再次驗證了將跳躍部分作為資產收益方差來源的重要性。

對依據流動性分類的三組股票進行分析時，我們有如下結論：(1)流動性高的股票呈現出指示存在跳躍的統計量極限值，而流動性弱的股票則因為噪音主導無法顯示。雖然跳躍行為的形成機制沒有達成廣泛的共識，但是其與信息相關則被諸多研究證實，例如Pierre 等在應用2006年至2008年道瓊斯股票所做的實證中，證明了90%的跳躍都是被過度檢出的，其余真實的跳躍與新聞、公告以及事件有關，大多數新聞不會導致跳躍，而只是產生波動率異象的市場反應。若跳躍的發生是由信息或信息披露前的流動性變化導致的，則跳躍是流動性好的股票及時消化和反映了這一信息的表征，而流動性差的股票則因為買賣價差大、交易者信念異質程度高，噪音顯著。(2) 流動性高的股票不但顯示存在跳，而且不同于其他兩類圖示仍然被噪音影響的情況，無限小跳的存在性也可以被看出，同時，流動性越高，這種極限的特征越明顯。由此可見，我國漲跌停制度、整手買入等限制性的交易制度等可能成為小跳產生的原因。Christensen 等最新基于超高頻數據或逐筆交易數據也發現，以往通過設定最佳的抽樣頻率來消除或減少微觀結構噪聲的非參數跳躍檢驗方法可能忽略掉微觀結構噪聲隱含的重要信息，過高估計了金融高頻時間序列中跳躍發生概率，而檢測到跳躍有可能是由于市場摩擦引起的微觀結構噪聲。(3)流動性高的股票顯示出比其他兩類更低的布朗運動占比，再次驗證了流動性高的股票收益過程中存在跳，同時，這還在一個側面反映出流動性高的股票反應信息的即時性。可以看出，若A 股市場中股票的流動性增強，噪音交易者減少，分析將變得更加清晰，數據反映出的信息會具有更高的可信度。

中國股市是否存在跳，跳躍活動是否有限，是否存在布朗運動，隨機波動率占已實現波動率的比重這些表面的測度所反映的市場內在的本質是什么，本文所研究的行業間的差別以及流動性的差別，背后可能是影響不同股票的信息的共享速度與非對稱性，以及不同投資者的行為特征。如何合理地測定這些因果邏輯鏈條、揭示價格路徑的形成機制以及股市的運作機制是今后有待研究的問題。

[1] Barndorff-Nielsen O E, Shephard N. Power and bipower variation with stochastic volatility and jumps [J]. Journal of Financial Econometrics,2004, 2(1)：1-48.

[2] Jacod J. Asymptotic properties of realized power variations and related functionals of semimartingales[J]. Stochastic Processes and their Applications, 2008,118(4)：517-559.

[3] Mancini C. Estimating the integrated volatility in stochastic volatility models with Levy type jumps[J]. Astronomy & Astrophysics,2006.

[4] Mancini C. Non parametric threshold estimation for models with stochastic diffusion coefficients and jumps[J].Scandinavian Journal of Statistics, 2009, 36(2): 270-296

[5] Zhang Lan.Efficient estimation of stochastic volatility using noisy observations: A multi-scale approach[J].Bernoulli,2006, 12(6):1019-1043.

[6] Zhang Lan, Mykland P A, Xt-Sahalia P A.A tale of two time scales: Determining integrated volatility with noisy high frequency data[J].Journal of the American Statistical Association,2005, 100(472):1394-1411.

[7] Barndorff-Nielsen O E, Hansen P R, Lunde A, et al.Designing realised kernels to measure the ex-post variation of equity prices in the presence of noise[J].Econometrica, 2008,76(6):1481-1536.

[8] Zhou Bin.High-frequency data and volatility in foreign-exchange rates[J]. Journal of Business and Economic Statistics, 1996,14(1): 45-52.

[9] Jacod J, Li Yinqing, Mykland P A, et al.Microstructure noise in the continuous case: The pre-averaging approach[J].Stochastic Processes and their Applications, 2009,119(7):2249-2276.

[10] Podolskij M, Vetter M.Estimation of volatility functionals in the simultaneous presence of microstructure noise and jumps[J].Bernoulli, 2009,15(3):634-658.

[11] Andersen T G, Bollerslev T, Diebold F X, et al.The distribution of realized stock return volatility[J].Journal of Financial Economics,2001, 61(1): 43-76.

[12] Bandi F M,Russell J R.Microstructure noise, realized variance, and optimal sampling[J]. Review of Economic Studies, 2006,75(2): 339-369.

[13] Bollen B, Inder B.Estimating daily volatility in financial markets utilizing intraday data[J].Journal of Empirical Finance,2002, 9(5):551-562.

[14] Hansen P R, Large J, Lunde A.Moving average-based estimators of integrated variance[J].Econometric Reviews, 2008,27(1-3):79-111.

[16] Fan Jianqing, Wang Yazhen. Multi-scale jump and volatility analysis for high-frequency financial data[J].Journal of the American Statistical Association,2007, 102(480):1349-1362.

[17] Barndorff-Nielsen O E, Shephard N.Econometrics of testing for jumps in financial economics using bipower variation[J].Journal of Financial Econometrics,2006, 4(1):1-30.

[18] Jiang G J， Oomen R C A.Testing for jumps when asset prices are observed with noise a “swap variance” Approach[J].Journal of Econometrics,2008, 144(2):352-370.

[19] Lee S S，Mykland P A.Jumps in financial markets: A new nonparametric test and jump dynamics[J]. Review of Financial studies, 2008,21(6): 2535-2563.

[20] A?t-Sahalia Y, Jacod J. Testing for jumps in a discretely observed process[J]. Annals of Statistics, 2009b,37(1):184-222.

[21] 胡素華, 張世英, 張彤. 雙指數跳躍擴散模型的 MCMC 估計[J]. 系統工程學報, 2006, 21(2): 113-118.

[22]任楓, 汪波, 段晶晶. 非對稱雙指數跳躍擴散模型的 MCMC 估計[J]. 系統工程, 2009, 27(7): 39-42.

[23] 馬宇超, 陳敏, 蔡宗武,等.中國股市權證定價的帶均值 回歸跳躍擴散模型[J]. 系統工程理論與實踐，2010,30(1):14-21.

[24] 曹宏鐸, 李旲, 何智. 股票價格運行的冪律特征及冪 律跳躍擴散模型[J]. 管理科學學報, 2011, 14(9): 46-59.

[25] 陳國進, 王占海. 我國股票市場連續性波動與跳躍性 波動實證研究[J]. 系統工程理論與實踐，2010，30 (9):1554-1561.

[26] 楊科, 陳浪南. 基于C_TMPV 的中國股市高頻波動 率的跳躍行為研究[J].管理科學, 2011, 24(2): 103-112.

[27] 唐勇, 張伯新. 基于高頻數據的中國股市跳躍特征實 證分析[J].中國管理科學, 2013, 21(5):29-39.

[28] 歐麗莎, 袁琛, 李漢東. 中國股票價格跳躍實證研究 [J]. 管理科學學報, 2011, 14(9): 60-66.

[29] 馬丹, 尹優平. 噪聲, 跳躍與高頻價格波動——基于 門限預平均實現波動的分析[J]. 金融研究, 2012 (4): 124-139.

[30] 唐勇, 寇貴明. 股票市場微觀結構噪聲, 跳躍, 流動 性關系分析[J].中國管理科學, 2012,20(2): 11-19.

[31] A?t-Sahalia Y, Mykland P A, Zhang Lan. How often to sample a continuous-time process in the presence of market microstrutcture noise[J].Review of Financial Studies ,2005,18 (2): 351-416.

[32] A?t-Sahalia Y, Jacod J. Estimating the degree of activity of jumps in high frequency data[J].The Annals of Statistics , 2009a,37 (5A): 2202-44.

[33] A?t-Sahalia Y, Jacod J. Is brownian motion necessary to model high-frequency data[J].The Annals of Statistics, 2010, 38 (5): 3093-3128.

[34] A?t-Sahalia Y, Jacod J. Testing whether jumps have finite or infinite activity[J].The Annals of Statistics, 2011,39 (3): 1689-1719.

[35] A?t-Sahalia Y, Mykland P A, Zhang Lan.Ultra high frequency volatility estimation with dependent microstructure noise[J]. Journal of Econometrics,2011,160(1):160-175.

[36] A?t-Sahalia Y, Jacod J.Analyzing the spectrum of asset returns: Jump and volatility components in high frequency data[J]. Journal of Economic Literature, 2012, 50(4): 1007-1050.

[37] Merton R C. Option pricing when underlying stock returns are discontinuous[J].Journal of Financial Economics ,1976,3 (1-2): 125-44.

[38] Ball C A, Torous W N. A simplified jump process for common stock returns[J].Journal of Financial and Quantitative Analysis,1983, 18 (1): 53-65.

[39] Bates D S. The crash of ’87: Was it expected? The evidence from options markets[J].The Journal of Finance,1991,46 (3): 1009-1044.

[40] Darrell D, Pan Jun, Singleton K.Transform analysis and asset pricing for affine jump-diffusions[J].Econometrica ,2000,68 (6): 1343-76.

[41] Barndorff-Nielsen O E. Normal inverse gaussian distributions and stochastic volatility modelling[J].Scandinavian Journal of Statistics,1997, 24 (1): 1-13.

[42] Barndorff-Nielsen O E. Processes of normal inverse gaussian type[J].Finance and Stochastics,1997, 2(1): 41-68.

[43] Carr P, Geman H, Madan D B,et al. The fine structure of asset returns: An empirical investigation[J].The Journal of Business,2002, 75 (2):305-32.

[44] Carr P, Wu Liuren. The finite moment log stable process and option pricing[J].Journal of Finance, 2003, 58 (2): 753-77.

[45] Carr P, Wu Liuren. Time-changed Levy processes and option pricing[J].Journal of Financial Economics ,2004,71 (1): 113-41.

[46] Mancini C. Disentangling the jumps of the diffusion in a geometric jumping brownian motion[J].Giornale dell’Istituto Italiano Attuari ,2001,64:19-47.

[47] Huang Xin, Tauchen G. The relative contribution of jumps to total price variance[J]. Journal of Financial Econometrics ,2005,3 (4): 456-99.

[48] Andersen T G. Tim Bollerslev, and Francis X.Diebold. Roughing it up: Including jump components in the measurement, modeling, and forecasting of return volatility[J].Review of Economics and Statistics,2007,89 (4): 701-720.

[49] Cont R, Mancini C. Nonparametric tests for pathwise properties of semimartingales[J].Bernoulli ,2011,17 (2): 781-813.

[50] Todorov V, Tauchen G. Activity signature functions for high-frequency data analysis[J].Journal of Econometrics,2010, 154 (2): 125-38.

[51] Belomestny D. Spectral estimation of the fractional order of a Levy process[J].The Annals of Statistics,2010,38 (1): 317-51.

[52] Hasbrouck J. Assessing the quality of a security market: A new approach to transaction-cost measurement[J].Review of Financial Studies ,1993,6 (1): 191-212.

Analysis of the Finer Statistical Characteristics of China Stock Market Based on Semimartingales Process

LIU Zhi-dong, YAN Guan

(School of Management Science and Engineering, Central University of Finance and Economics,Beijing 100081,China)

In this paper the different asymptotic behavior of the power variations is exploited as the power p, the truncation level and the sampling frequency are varying,and test statistics is developed on the realized power variation, then a systematic econometric analysis of stochastic volatility ,jump and noise existing in high frequency financial returns is given based on Semimartingales Process, asset returns sampled at high frequency are decomposed into their base components (continuous, small jumps, large jumps), the relative magnitude of the components is determined, considering market microstructure noise. The methodology is applied to individual stock returns from different industries, those with different liquidity as well as stock index returns and its constituent stocks. Our results show that noisy traders exist widely in CSM; 43% risk results from stochastic volatility risk in asset return process, possibly hedged by equity option; the importance order of risk from different sources is stochastic volatility, systemic jump and heterogeneous jump; more liquid equities have more significant proof of jump, especially infinite small jumps.

high-frequency data;semimartingales;jump; noise; liquidity

1003-207(2016)05-0018-13

10.16381/j.cnki.issn1003-207x.2016.05.003

2015-06-01；

2015-10-13

國家自然科學基金資助項目(71271223,70971145)；教育部新世紀人才支持計劃(NECT-13-1054)

簡介：劉志東(1973-)，男(漢族)，內蒙古赤峰人，中央財經大學管理科學與工程學院博士，教授，博士研究生導師，研究方向：金融工程與金融計量，Email：liu_phd@163.com.

F830.9

A