基于Benders分解算法的跨區互聯電力系統協調規劃模型
薛 松,曾 博,王躍錦
(1.國網能源研究院,北京 102209;2.華北電力大學新能源電力系統國家重點實驗室,北京 102206;3.冀北電力有限公司北京送變電公司,北京 102401)
?
基于Benders分解算法的跨區互聯電力系統協調規劃模型
薛 松1,曾 博2,王躍錦3
(1.國網能源研究院,北京 102209;2.華北電力大學新能源電力系統國家重點實驗室,北京 102206;3.冀北電力有限公司北京送變電公司,北京 102401)
研究跨區互聯電力系統的協調規劃,對于提高投資效率實現更大范圍的資源配置具有較強現實意義。本文首先描述多區域電力系統擴張規劃問題,并建立多區域擴張規劃模型,旨在尋求最優的擴容方案,以最小投入來滿足多區域電力系統負荷增長需求;其次,采用Benders分解算法將多區域擴張規劃問題分解為一個規劃主問題和一個運行子問題,通過主子問題之間的迭代求解,獲得最終的最優解;最后,對某個典型的包含7個區域的多區域電力系統進行模擬仿真,驗證了本文所構建模型及算法的有效性。
多區域;電力系統互聯;發輸電擴張規劃;Benders分解算法
1 引言
我國電力系統面臨電源結構不合理,資源和負荷中心逆向分布,西部電力送出困難,電源電網缺乏統一規劃等問題[1]。跨區互聯電力系統協調規劃是通過實現不同地區不同發電資源的協調規劃,以及發電資源和輸電線路的協調規劃投資,提高資源配置效率,實現整體投資最優[2],能夠有效促進電能互補及利用,提高整個電力系統的經濟效益和社會效益,實現電力資源的大范圍優化配置[3]。對于促進我國偏遠地區煤電、風電及水電基地電能輸送到東部負荷中心消納,具有較強的現實意義。隨著偏遠地區能源基地以及特高壓輸電通道的全面建設,面臨的一個重要課題就是如何實現跨區電力系統的協調規劃,提高投資效率,促進跨區電力投資的有序發展。因此,亟需開展跨區電力系統協調規劃模型研究[4-5]。
目前,國內外與跨區電力系統相關的研究主要集中在系統交易和調度方面[6-8],針對電力系統規劃的研究,主要集中在單一的電源規劃和電網規劃,張新華[9]分析了投資政策不確定條件下的寡頭發電容量規劃方法,李翔等[10]對粒子群算法進行優化應用在電源規劃中,張新華等[11]研究了寡頭發電商發電容量規劃模型,王秀麗等[12]對多區域電網規劃問題進行研究,并將協同進化算法和NSGA-II算法相結合用于算例求解,但并未考慮區域中電源規劃問題。總體看來,目前針對電源、電網協調規劃的研究還較少,針對跨區互聯電力系統的電源、電網協調規劃的研究更少,而跨區互聯電力系統規劃中,由于資源的區域分布特點使得電源情況更為復雜,要實現更大范圍的資源優化配置,跨區互聯電力系統的電源和電網協調規劃也更為復雜。基于此,本文針對跨區互聯電力系統,研究多區域互聯電源電網協調規劃問題,具有更高的理論價值和現實意義。
本文首先構建跨區互聯電力系統規劃目標函數,滿足多區域電力系統負荷增長需求時整體投資成本最小;其次,采用Benders分解算法將跨區互聯電力系統規劃問題分解為一個規劃主問題和一個運行可靠性子問題,通過主子問題之間的迭代求解,獲得最終的最優解;最后,以某包含7個區域電網的跨區互聯電力系統為例進行模擬仿真,驗證本文所構建的模型及方法的有效性。文中的協調有兩方面的含義:一是區域之間各種發電資源的協調規劃,二是跨區聯絡線的協調,也可以理解為整個電力系統中的發輸電協調規劃,協調規劃的目標是既要滿足整個系統的負荷需求和安全穩定運行需求,又要滿足投資成本最小經濟最優。
2 跨區互聯電力系統協調規劃目標函數
跨區互聯電力系統是由多個控制區域通過聯絡線聯接起來的互聯系統,每個區域都是獨立的經濟實體。跨區電力系統互聯可獲得兩方面的效益:一方面是系統運行的效益,主要包括各系統間電負荷的錯峰效益、提高系統安全可靠性的效益、互聯區域系統調峰能力互相支援、互為備用調峰的效益以及增強系統抵御事故能力的效益[13];另一方面是系統投資的效益,主要體現在大范圍資源的調用,減少新增系統裝機容量、輸電線路的投資[14]。
這些效益在經濟上可以歸納為投資和運行成本的節約[15]。跨區電力系統協調規劃問題正是從多區域電力系統出發,通過合理安排各區域中候選發電機組以及輸電線路的投資,使其在滿足系統運行約束、可靠性約束以及各發電機組相關物理約束的前提下,使得系統總成本最小。
跨區電力系統協調規劃模型以整個系統總成本最小為目標函數,其中系統總成本包括系統總投資成本和運行成本與殘值的差,如式(1)所示:
min(IC+OC-SV)
(1)
式中,IC為總的投資成本;OC為總的運行成本;SV為總殘值。
系統總投資成本是指新增發電機組投資成本和新建輸電線路的投資成本之和,如式(2)所示:
ξtICl(ylt-yl(t-1))
(2)
其中:
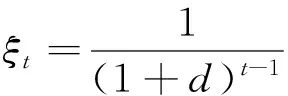
(3)
式中,ξt為第t年的現值系數;ICi為發電機組i的投資成本;zit為第t年發電機組i的安裝狀態,1為已安裝,否則為0;ICl為輸電線路l的投資成本;ylt為第t年輸電線路l的安裝狀態,1為已安裝,否則為0;CG為區域內所有候選發電機組的集合;CL為區域內所有候選輸電線路的集合;d為貼現率。
運行成本包括火電機組、水電機組和可再生能源機組的固定運維成本以及可變運維成本兩部分,如式(4)所示:
(4)
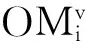
殘值是規劃期末發電機組和輸電線路的最終剩余價值,引入現值系數將殘值折現到期初并計入系統總成本中,如式(5)所示:
πltICl(ylt-yl(t-1))
(5)
式中,ξT為第T年的折現系數;πit為第t年發電機組i的殘值;πit為輸電線路l的殘值;T為規劃周期。
3 基于Benders分解算法的跨區互聯電力系統規劃問題求解
本文所研究的多區域擴張規劃問題是混合整數規劃問題(MixedIntegerProgramming,MIP),廣泛使用的求解混合整數規劃的方法有割平面法和分支定界法。但是隨著求解問題變量數目的增加,割平面法和分支定界法往往很難奏效,在實際運用中效果不佳[16]。因此,本文通過Benders分解算法對多區域擴張規劃問題進行分解,來求解該MIP問題[17-18]。Benders分解算法已在生產領域如生產調度、協同運輸的路線整合等問題求解中得到了應用,本文主要對Benders分解算法的應用進行了擴展和創新,將該方法用于解決跨區互聯電力系統的協調規劃問題。
3.1Bender分解算法
Benders分解算法通過迭代求解包含復雜變量的混合整數規劃問題。本節將詳細給出Benders分解算法的基本原理。
考慮如下混合整數線性規劃(MIP)問題:
maxaTx+bTy
s.t.Ax+By≤m
x∈Rn
y∈Zm
(6)
其中變量y為“復雜變量”,它的存在增加了MIP問題的求解難度,如果可以固定它的值,問題的求解將變的相對簡單。式(6)可以表示為:
max{bTy+max(aTx|Ax≤m-By)}
(7)
當整數變量y固定后,得到一個與y有關的線性規劃問題,即式(7)括號中的極大值問題:
maxaTx
s.t.Ax≤m-By
x∈Rn
(8)
其對偶問題為:
mincT(m-By)
s.t.ATc≥a
c∈Rm
(9)
若Q={c∈Rm|AT≥a}為空集,則對偶問題(9)無可行解。由對偶定理可知,問題(8)或者無界或者是不可行的。
不妨假設Q≠Ф,則凸多面體Q與y無關,不論y取值如何,Q上cT(m-By)的極小值在它的頂點取得或者沿著它的極方向無限減少。假設可行域Q的極方向集為vs,極點集為cp。則MIP問題可以寫成如下形式:
max {bTy+min(cp)T(m-By)}
s.t. (vs)T(m-By)≥0,s∈S
y∈Zm
(10)
式(10)等價于:
maxω
s.t.ω≤{bTy+min(cp)T(m-By)},p∈P
(vs)T(m-By)≥0,s∈S
y∈Zm
(11)
一般把問題(11)稱為主問題,把問題(8)稱為子問題,由子問題對偶問題可行域對應的極點和極方向構成的約束即為Benders割。可以看出,Benders分解算法實施過程中,子問題基于對偶原理單獨求解,并返回給主問題最優解的信息,主問題根據子問題返回的信息給出主問題的目標最優解,通過反復迭代并最終收斂到最優解。
3.2Benders算法的分解結構
利用Benders分解原理求解多區域電力系統擴張規劃問題的基本思想是將原問題分解為1個混合整數規劃主問題和1個線性規劃子問題,通過主問題和子問題之間的迭代求解,獲得最終的最優解[19]。其中,主問題是不考慮可靠性的多區域最優擴張規劃問題,子問題是考慮可靠性的跨區互聯電力系統最優運行問題。
在主問題中,跨區域互聯電力系統投資以年為單位進行分析,投資商向電力系統提供發電機組和輸電線路的候選集,考慮規劃限制情況下,電力系統以新機組和新線路投資總成本最小化為目標,確定新機組和線路的最優投資方案。其中,規劃限制因素包括機組和線路最大數量以及候選機組和線路的建設時間等。除了規劃限制因素,子問題中產生的Benders割也作為主問題附加約束條件,對主問題的組合優化狀態進行修正。主問題中包含所有的變量,而且所有的限制條件是線性的。主問題是一個混合整數線性規劃問題。
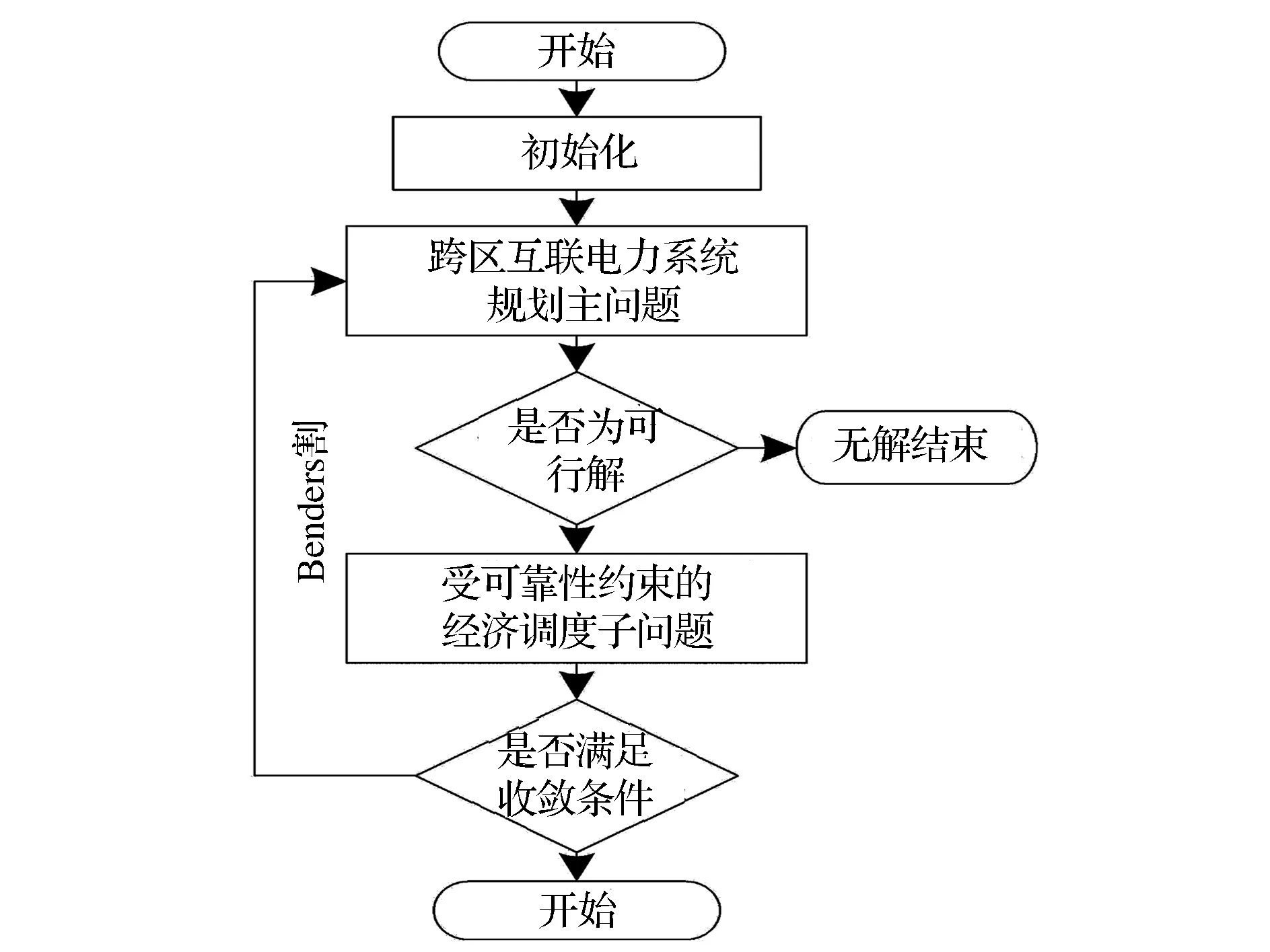
在主問題給定跨區互聯電力系統規劃狀態的情況下,跨區互聯電力系統規劃問題又轉變成為一個經濟性的調度問題。該子問題以運行成本最小化為目標,不僅保證每個節點是電力平衡的,而且滿足可靠性和發電機組物理限制因素的要求。在運行可靠性不通過的情況下,會形成Benders割,用以分析主問題中規劃問題的派生情況。Benders割添加到主問題中將會修正主問題優化空間。其基本過程如圖1所示。
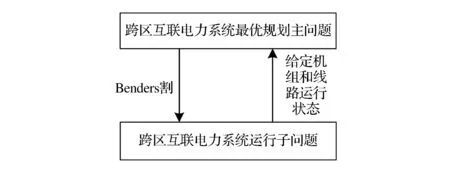
圖1 Benders分解結構框圖
3.2.1 投資規劃主問題
主問題研究最優投資規劃,子問題進行可靠性檢驗并確定最優運行狀態。在Benders分解結構中,主問題確定最優投資規劃,其目標是新增發電機組和輸電線路的投資成本最小,如式(12)所示。
(12)
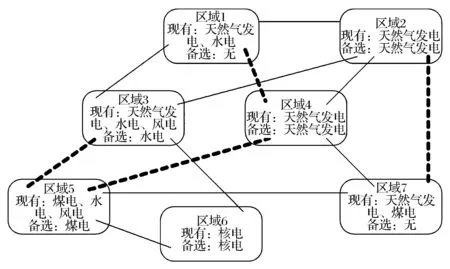
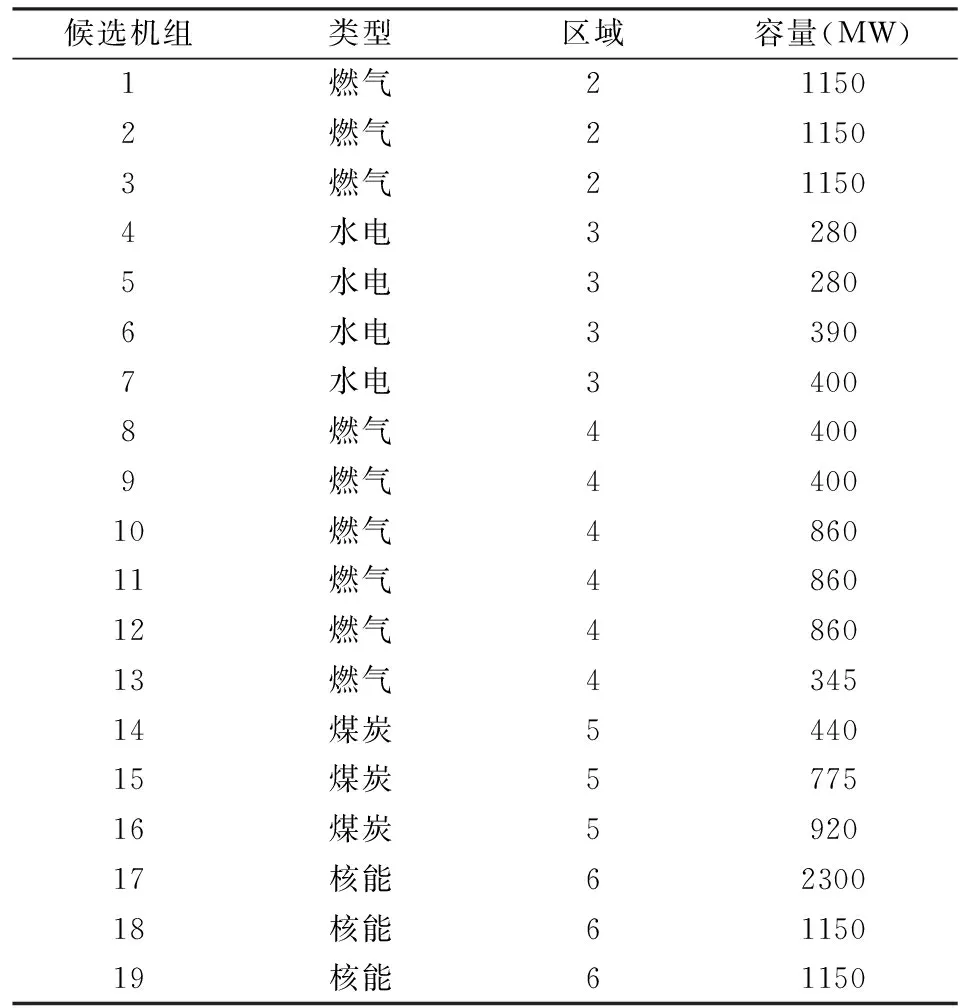
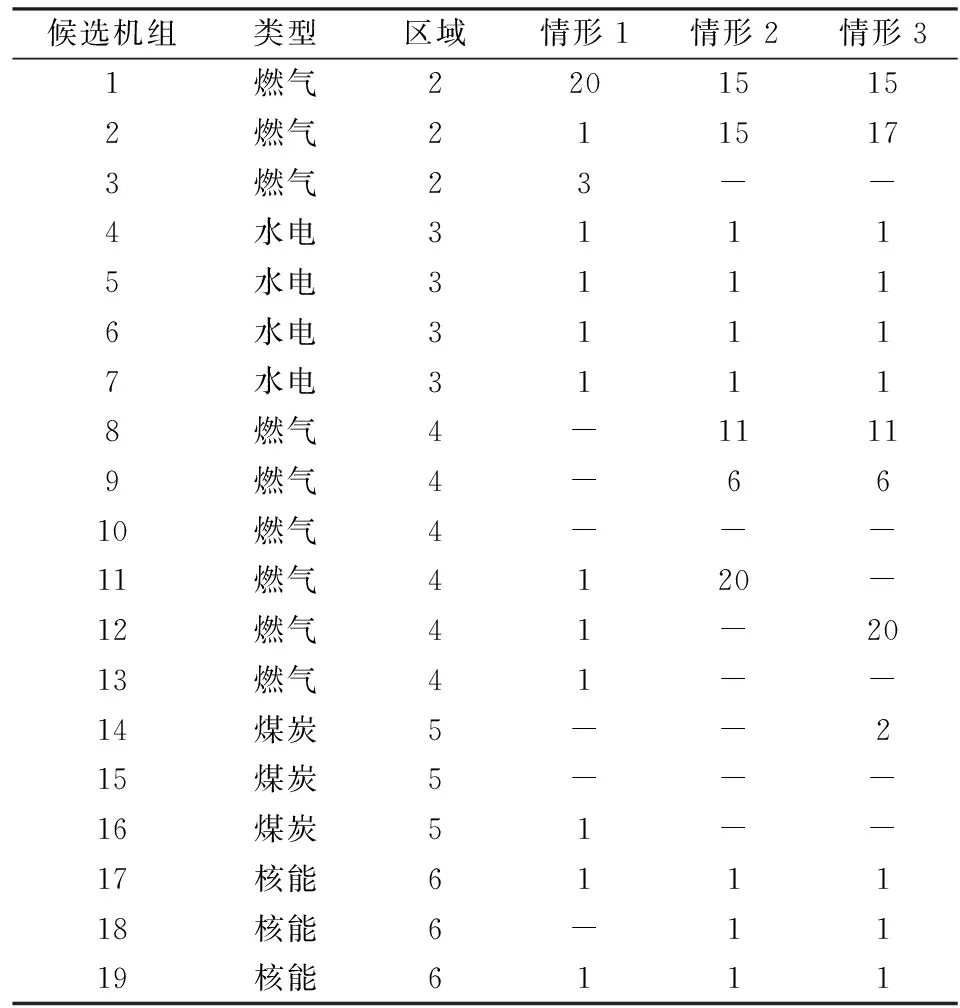
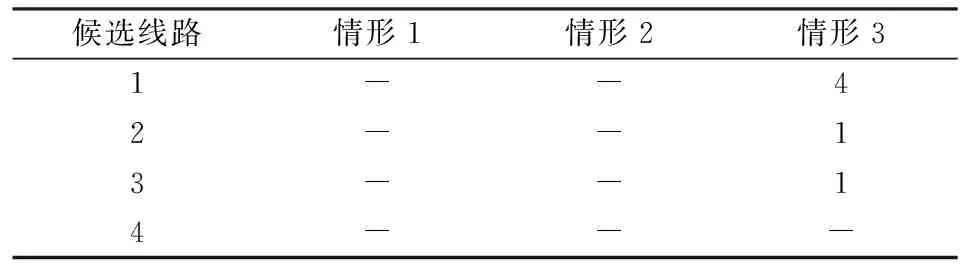
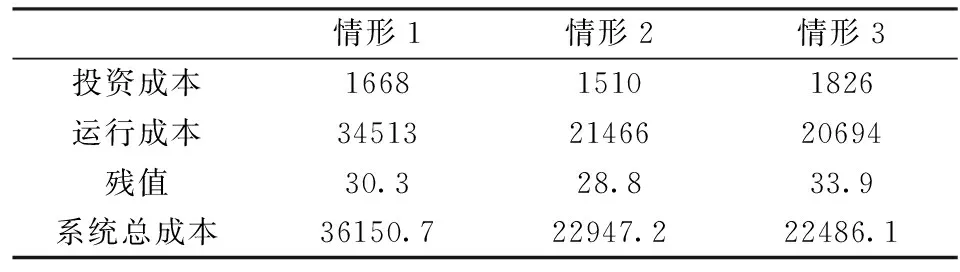
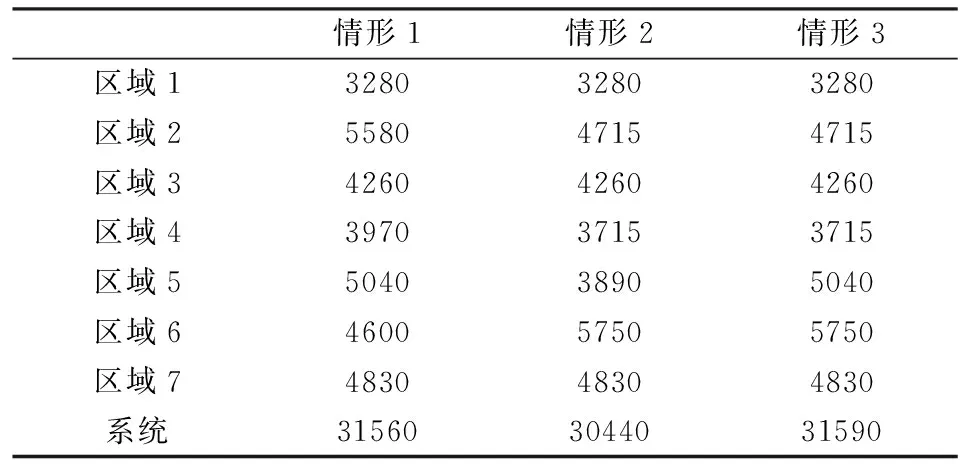
s.t.zit=0 ?i∈CG,?t (13) ylt=0 ?l∈CL,?t (14) zi(t-1)≤zit?i∈CG,?t (15) yl(t-1)≤ylt?l∈CL,?t (16) Iiht≤zit?i∈CG,?b,?h,?t (17) (18) 式中:zit為第t年發電機組i的安裝狀態;ylt為第t年輸電線路l的安裝狀態;Ti,bt為發電機組i的建設時間;Tl,bt為輸電線路l的建設時間;Iiht為第t年時段h內發電機組i的啟停狀態,1為開機,0為停機;Pi,max為發電機組i的最大發電出力;ET為區域內現有火電機組的集合;CT為區域內候選火電機組的集合;EH為區域內現有水電機組的集合;CH為區域內候選水電機組的集合;R為系統旋轉備用需求;αiht、βiht、δiht、λlht、γlht、ηlht分別為優化過程中對應于各約束的拉格朗日乘子最優值,均為常數。其中,式(13)—(17)分別為發電機組和輸電線路的建設時間約束條件、裝機情況約束條件、發電機組的組合優化狀態約束條件,式(18)為Benders割的表達式。 3.2.2 受可靠性約束的經濟調度子問題 在主問題確定第t年發電機組i的安裝狀態zit以及輸電線路l的安裝狀態ylt后,運行子問題是跨區互聯電力系統經濟調度模型,并檢驗所求解的可靠性。目標函數是基于主問題產生的投資規劃和機組組合優化狀態下的系統運行成本最小問題,如式(19)所示。 (19) (20) (21) Pi,minIihtXith≤Piht≤Pi,maxIihtXith (22) (23) |Dlht|≤Pi,maxYlht (24) Piht-Pi(h-1)t≤[1-Mmhtk(1-Ii(h-1)t)]Ri+Miht(1-Ii(h-1)t)Pi,min (25) (26) 隨機規劃解將滿足長期可靠性指數,如組件事故停機率LOLE。當第t年h時段的LOLE值比其目標值大時,第r次迭代時產生Benders割,相應的可靠性信號會反饋給主問題。將LOLE作為約束條件限制的每小時事故停機率,使用基于小時指標的優點在于能夠阻止某些時段發生大規模甩負荷的情況。式(27)為LOLE的計算公式,式(28)為可靠性約束條件,如果式(27)中的式子不能滿足,則會產生Benders割。 (27) (28) 基于Benders分解算法的跨區互聯電力系統協調規劃問題求解流程框圖如圖2所示。 圖2 基于Benders分解算法的跨區互聯電力系統協調規劃求解流程 基本步驟如下: 1)初始化。設定跨區互聯電力系統規劃主問題的初始可行解,即能夠滿足機組和線路最大數量以及候選機組和線路的建設時間的新機組和線路的最優投資方案。 2)求解跨區互聯電力系統規劃主問題。由子問題最優解計算Benders割,得到約束(18)。求解主問題,得到發電機組i的最優安裝狀態zit*和輸電線路l的最優安裝狀態ylt*,以及式(1)最優解T。如果S≤T+ε,則結束迭代,轉輸出最優解,否則轉入步驟(4)。 3)求解跨區互聯電力系統受可靠性約束的經濟調度子問題。根據主問題最優解,求解經濟調度子問題,這里用到并行計算,通過計算得到各時段各機組的最優出力Piht*和最優拉格朗日乘子αiht、βiht、δiht、λlht、γlht、ηlht。求出此時式(1)的值,即為子問題得到的最優值,記為S。 4)檢驗zit*和ylt*的可行性,若可行,則轉入步驟3);否則,轉入步驟2),采取措施重新設定zit*和ylt*。 圖3所示的多區域電力系統是本文的研究對象,該系統被分為7個區域,由8條線路互聯。現有54個發電機組,其中43臺熱能機組、9臺水電機組、2臺風電機組[18];候選發電機組有19臺,其中12臺火電機組、4臺水電機組、3臺核電機組,候選輸電線路有4條。設定規劃時間范圍為20年,每年被劃分為6個周期,即每個周期時長兩個月。規劃期初該多區域系統現有裝機容量為23500MW,隨著時間的推移,老電機組退役,在規劃期末共有11臺機組退役,裝機容量降到20680MW。候選發電機組及輸電線路參數分別如表1和表2所示,假定規劃期初該多區域系統的負荷是10300MW,負荷年均增長率為2.6%。設定旋轉備用需求為負荷的5%;不限制每年的投資額以及機組或線路的安裝數量,并忽略單個區域的輸電阻塞,區域輸電阻塞也暫不考慮;假定所有區域的LOLE目標值一致;貼現率為5%。 圖3 多區域電力系統 算例仿真模擬在CPLEX11.0環境下進行,優化計算通過調用CPLEX優化工具箱和Linprog函數來完成。為驗證本文所提模型及算法的有效性,對三種情形下的模擬結果進行對比分析。三種情形如下所示: 情形1:規劃期內,在各個區域內實施發輸電擴張規劃,不考慮區域內的發輸電之間的協調規劃; 情形2:規劃期內,在該多區域電力系統內實施發輸電擴張規劃,不考慮發輸電之間的協調規劃; 情形3:規劃期內,在該多區域電力系統內實施發輸電協調擴張規劃。 表1 候選發電機組相關參數 表2 候選輸電線路相關參數 算例模擬結果如表3-表6所示。 表3 候選機組裝機年份匯總表 表4 候選線路裝機年份匯總表 表5 多區域電力系統成本 單位:億元 在情形1中,由于無法從其他資源豐富的地區獲取成本較低的發電資源,因此,為了滿足快速增長的區域電力需求,這些地區不得不開發利用區域內經濟性較差的發電資源,這帶來了較高的投資成本和運行成本。 在情形2中,資源豐富的地區可以投資建設更多的經濟性較高的發電廠,并將電力傳輸到資源相對緊張的地區,以取代部分高成本燃料供電,進而降低總成本。和情形1相比,經濟型機組在區域6安裝,代替區域2和4中經濟性較差的機組,減少了系統成本。情形2的系統總成本是22947.2億元,與情形1相比降低了36.5%,其中投資成本和運行成本都有所減少。 在情形3中,除了考慮區域間電力交易外,還需要考慮發電和輸電之間的協調規劃間。從表4結果可以看出,規劃期內,候選線路1、2、3投資建設,這是因為它們會降低線路1和2中的輸電阻塞,并且有助于區域5中經濟型機組的發電調度。通過安裝這些候選線路,區域5也可以安裝并使用14號機組,從而能夠在不依靠其他區域的情況下滿足自身電力需求,并可以對其他區域容量缺乏進行補償。從表5結果看出,情形3的系統總成本是22486.1億元,與情形1相比降低了37.8%,與情形2相比降低了2.0%。情形3的規劃成本是1826億元,與情形2相比增加了316億元,但情形3減少了772億元的運行成本,總的來說,情形3比情形2更具經濟性。 表6 各個區域電力系統裝機容量 單位:MW 表6顯示了各個情形中各區域的裝機容量,可以看出,情形1中的發電裝機最高,這雙由于缺少區域間的電力交易,各區域的電力需求只能通過各自區域自身的發電機組來提供;情形3中,14號機組的投資建設增加了系統的總裝機,因此其裝機容量略高于情形2的。 本文針對多區域擴張規劃問題,構建了以包含投資成本、運行成本和殘值的系統總成本最小化為目標的多區域擴張規劃模型;并利用Benders分解算法將原問題分解為1個混合整數規劃主問題和1個線性規劃子問題,對某個典型的包含7個區域的多區域電力系統進行仿真模擬,通過主子問題之間的迭代,求得最優解,驗證了本文所構建的模型及算法的有效性。研究結果表明,本文構建的多區域規劃模型考慮到了區域內的發輸電之間的協調規劃及區域間的電力交易,可以大幅度降低電力系統成本,且指出了規劃期各階段各發電機組類型的最優組合以及開發的優先程度,為發電企業提供了決策依據,對政策制定者也具有參考價值。 目前,我國電力規劃管理工作較薄弱,還沒有統一規劃機制,模型參數收集面臨挑戰。在電力統一規劃機制建立前,協調規劃工作應仍由政府部門主導,加強數據收集、歸檔等基礎工作。由各地區上報相關的發電和電網數據,通過協調規劃模型最終制定規劃方案。 [1]ZengMing,XueSong,ZhuXiaoli,etal.China's12thFive-yearplanpushespowerindustryinnewdirections[J].Power,2012,156(1):50-55. [2]LiuGuoping,XuZheng,HuangYing,etal.Analysisofinter-areaoscillationsintheSouthChinaInterconnectedPowerSystem[J].ElectricPowerSystemsResearch,2004,70(1):38-45. [3] 柳瑞禹,葉子菀.高耗能行業電力消費長期波動效應研究[J].中國管理科學,2014,22(6):125-133. [4] 牛東曉,孟明.季節型增長趨勢電力消費預測研究:基于中國的實證分析[J].中國管理科學,2010,18(2):108-112. [5] 張運洲,胡泊.“三北”地區風電開發、輸送及消納研究[J].中國電力,2012,45(9):1-6. [6] 劉吉成,譚忠富,陳廣娟,等.差價合約下電網公司購電費用最小化的離散優化模型[J].中國管理科學,2007,15(6):60-66. [7] 黃守軍,任玉瓏,孫睿,等.基于碳減排調度的激勵性廠網合作競價機制設計[J].中國管理科學,2011,19(5):138-146. [8] 李小林,張松,陳華平.考慮分時電價的多目標批調度問題蟻群算法求解[J].中國管理科學,2014,22(12):56-64. [9] 張新華,葉澤.投資政策不確定條件下的寡頭發電容量投資分析[J].中國管理科學,2014,22(9):26-32. [10] 李翔,牛東曉,楊尚東.改進粒子群優化算法在電源規劃中的應用[J].中國管理科學,2006,14(6):113-118. [11] 張新華,賴明勇,葉澤.寡頭發電商投資閾值與容量選擇模型及其分析[J].中國管理科學,2010,18(5):106-112. [12] 王秀麗,李淑慧,陳皓勇,等.基于非支配遺傳算法及協同進化算法的多目標多區域電網規劃[J].中國電機工程學報,2006,26(12):11-15. [13]KimMK,HurD.Decomposition-coordinationstrategytoimprovepowertransfercapabilityofinterconnectedsystems[J].InternationalJournalofElectricalPower&EnergySystems,2011,33(10):1638-1647. [14]SpieckerS,VogelP,WebeC.EvaluatinginterconnectorinvestmentsinthenorthEuropeanelectricitysystemconsideringfluctuatingwindpowerpenetration[J].EnergyEconomics,2013,37:114-127. [15]ApaemmanouilA,TjernbergLB,TuanLA,etal.Improvedcost-benefitanalysisformarket-basedtransmissionplanning,aEuropeanperspective[J].EnergyPolicy,2013,63:215-223. [16] 李鐵克,蘇志雄.煉鋼連鑄生產調度問題的兩階段遺傳算法[J].中國管理科學,2009,17(5):68-74. [17] 翁克瑞,諸克軍,劉耕.協同運輸的路線整合問題研究[J].中國管理科學,2015,23(1):135-140. [18] 李穎浩,郭瑞鵬.基于廣義Benders分解的啟發式機組組合優化[J].電網技術,2012,36(3):179-183. [19] 薛松,王致杰,韓蕊,等.考慮風電并網的快速響應火電機組安全經濟規劃模型[J].電網技術,2013,37(10):2888-2895. Keywords:multi-area;interconnectedpowersystem;generationandtransmissionexpansionplanning;Bendersdecompositionalgorithm Multi-area Power System Coordinated Planning Model Based on Benders Decomposition Algorithm XUESong1,ZENGBo2,WANGYue-jin3 (1.StateGridEnergyResearchInstitute,ChangpingDistrict,Beijing102209,China;2.StateKeyLaboratoryforAlternateElectricalPowerSystemwithRenewableSources,NorthChinaElectricPowerUniversity,ChangpingDistrict,Beijing102206,China;3.BeijingElectricPowerTransmissionandTransportationCompany,JibeiElectricPowerCompanyLimited,FangshanDistrict,Beijing102401,China) Withtheacceleratingofgridinterconnectionpaceandinter-regionalpowertransmissionneedsbecomingincreasinglyprominent,thegenerationsideplanningandtransmissionsideplanfacesmoreuncertainties.Coordinationrequirementsbetweenthosearealsohigh.Therefore,inbackgroundofmulti-regionalpowersysteminterconnection,ithasimportanttheoreticalandpracticalsignificancetostudythegenerationandtransmissioncoordinatedexpansionplanningproblem.Firstly,multi-areapowersystemcoordinatedplanningproblemisdescribed,andthemulti-areacoordinatedplanningmodelisestablished,whichisaimedatfindingtheoptimalexpansionprogram.Themodelmeetsthemulti-areapowersystemgrowthloaddemandwiththeminimuminvestment.Secondly,theBendersdecompositionalgorithmisusedtodecomposethemulti-areaexpansionplanningproblemintoaplanningmasterproblemandarunningsub-problem.Throughiterativesolutionbetweenthemasterproblemandthesub-problem,thefinaloptimalsolutioncabeobtained.Finally,atypicalmulti-areapowersystemwhichconsistsofsevenregionsissimulated,toverifytheeffectivenessoftheconstructedmodelandalgorithm. 1003-207(2016)05-0119-08 10.16381/j.cnki.issn1003-207x.2016.05.014 2014-07-16; 2015-05-18 國家自然科學基金資助項目(71271082);國家電網公司科技項目(SGZB0000JYWT1400237);國家軟科學研究計劃(2012GXS4B064) 簡介:薛松(1986-),男(漢族),山東淄博人,國網能源研究院高級工程師,博士工程師,研究方向:能源與電力投資決策方法及理論,E-mail:xuesong@sgeri.sgcc.com.cn. C873;F224 A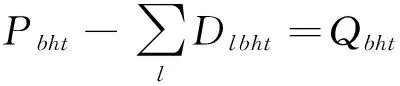
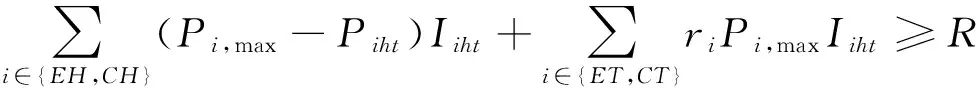

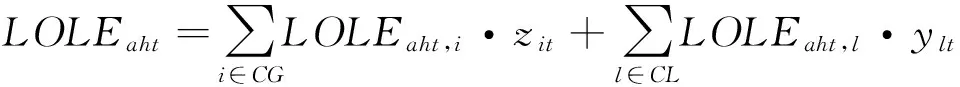
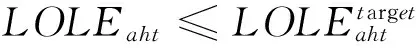
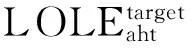
4 算例分析

5 結語

