試析導數在高中函數問題中的應用

湖南省瀏陽市田家炳實驗中學1407班 羊宇健

試析導數在高中函數問題中的應用

湖南省瀏陽市田家炳實驗中學1407班 羊宇健

歷年高考中，函數知識的考查一直是每年高考的熱點，而導數在函數問題中的應用，給我們解決函數問題增添了新的活力，尤其是在判斷函數的單調性、極值等方面有著廣泛的應用。下面，我就分享自己在導數學習中的一些感受和經驗供大家參考。

一、利用導數求函數的切線

例1 已知曲線y=x3-2x2+1 ，求經過點A（2,1）的切線方程。

解：當切點為點A時，將x=2代入y,=3x2－4x，得y′=4，利用點斜式，可得切線方程為4x-y+7=0；當切點不是點A時，不妨設切點為A0(x0,y0),則有y0＝x03－2x02＋1；（1）

利用點斜式，可得切線方程為y－1＝（3x02－4x0）（x－2）；（2）

結合（1）（2）兩式，可解得x0＝0,2，所以，過點A的切線有兩條，分別是y＝1和4x－y＋7＝0。

對于利用導數求函數的切線問題，我們要熟練掌握曲線y＝f（x）在A（x0，y0）處的切線斜率就是函數y＝f（x）在x0處的導數，其切線方程為y－y0＝f′（x）(x－x0），而很多學生常常忽略題目的要求，沒有弄清是求過切點的切線還是求該點為切點時的切線。因此，在做題時應仔細審題，確保答案正確無誤。

二、利用導數判斷函數的單調性

例2 已知函數y＝2x3－4x2＋2x，求該函數的單調區間。

分析：首先明確函數的定義域，求出該函數的導數為y′＝6x2－8x＋2；其次利用導數性質進行作答，即當y′＞0時，函數為單調增區間，y＝6x2－8x＋2＞0,求得x＞1或x＜;當y＜0時，函數為單調減區間，6x2－8x＋2＜0,求得＜x＜1。

在函數比較復雜時，我們常常利用導數判斷函數的單調性。對于利用導數判斷函數單調性問題，首先應求出函數的導數，并且確定出函數的定義域；其次，利用導數的符號判斷函數的單調性，即在函數的定義域內導數大于零，則為函數的增區間，導數小于零，則為函數的減區間。

三、利用導數求解函數的極值

例3 已知函數f（x）＝ex（x2＋ax＋a＋1），求該函數的極值個數。

解：函數f（x）的導數f′（x）＝ex（x2＋ax＋a＋1）＋ex（2x＋a）＝ex［x2＋（a＋2）x＋2a＋1]＝0，

由于ex恒大于0，所以x2+（a+2）x+2a+1＝0，

當△=0時，函數兩個相同的實根x1、x2，即（a+2）2－4（2a+1）＝0，求得a為0或4，故f′（x）=ex（x－x1）2，此時，恒有f′（x）＞0，因此，該函數沒有極值。

當△＞0時，函數有兩個不同的實根x1，x2，即（a+2）2－4（2a+1）＞0，求得a＜0或a＞4,為了研究方便，我們采用以下圖表進行分析：

x （-∞，x1） x1 （x1，x2） x2 （x2，+∞）f（x） + 0 - 0 +f（x） 遞增 極大值 遞減 極小值 遞增

當△＜0時，求得0＜a＜4，故f′（x）＝ex［x2＋（a＋2）·x＋2a＋1]恒大于零，則f（x）＝ex（x2＋ax＋a＋1）為增函數，此時該函數沒有極值。

一個函數能否取得極值的關鍵在于該點處導數是否為零且該點兩側是否異號，若該點的導數為零但該點兩側為同號，則該點仍然不是極值。對于利用導數求解函數極值問題，首先，仍然是求出函數的導數，并且確定出函數的定義域；其次，求出函數的導數的所有實根，然后利用表格的形式進行檢驗，確保該點左右兩側為異號。若是左正右負，則該點為極大值，反之，則為極小值。

四、利用導數求參數的范圍

例4 已知函數為f（x）=ax2-lnx-1有兩解，求參數a的取值范圍。

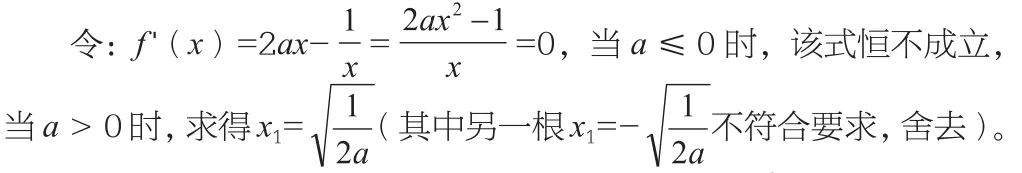
為了研究方便，根據題意，我們不妨描出f（x）=ax2-lnx-1的草圖，其函數草圖如下圖所示。

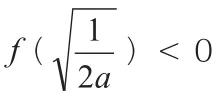
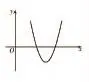
利用導數求參數的范圍，應將其轉換為不等式恒成立求解，通過這種逆向思維的轉換，最終轉換為函數的極值或最值問題進行求解。只有這樣，才能將復雜的數學問題簡單化。

五、利用導數解決函數實際問題

例題5 如圖所示，A廠位于河道邊，B廠位于距離河道40km處，并且A廠到B廠在河道上的垂直點D處的距離為50km，則怎樣修建一座供水站C廠，使C廠到A、B兩廠的管道鋪設費用最小？其中供水站到A、B兩廠的鋪設費用每千米分別為3a、5a元。

解法：不妨設CD=xkm，則AC=（50-x）km,,根 據 題 意，此題可以轉化為當x取何值時，鋪設費用取得最小值。

總之，導數應用于函數問題將使函數問題變得更加清晰和簡單，因此，在具體應用過程中，我們務必注重導數和函數基礎知識的理解，應用圖形結合思想，達到優化函數解題思維，簡化解題過程的目的。

（指導老師：湯華柏）