一元二次方程中的易錯題型小結

江西省贛州中學 黃學財

一元二次方程中的易錯題型小結

江西省贛州中學 黃學財

數(shù)學是每一名學生都想學好的學科，每個人的理解能力不一致，加上其他的一些因素，能把數(shù)學學得溜的學生不是特別多。在解數(shù)學問題時，會而不對、對而不全這種現(xiàn)象十分普遍，對于優(yōu)生來講如何減少失誤，發(fā)揮最大潛力，即減少非智力因素帶來的影響，是他們很關心的問題。解決這個問題的法寶，就是多總結，尤其是易錯題，要多歸類，列出易錯的知識點，舉一反三，達到觸類旁通的目的。

一元二次方程；系數(shù)；實際問題

一元二次方程是初中階段最難學的方程，也起著承上啟下的作用，為后續(xù)高中學好二元方程打下扎實的基礎。一元二次方程重點在于它的解法，從課本上看出，一元二次方程的解法由最簡單的直接開平方法到因式分解法，層層推進，一元二次方程的解法還是有較多學生過不了關，出現(xiàn)的主要問題是公式不熟、符號問題、方法選擇不恰當、未排根等，尤其是一元二次方程的綜合運用問題，不僅考查學生的文字理解能力，更考查學生的運算與思維能力。為幫助學生在解一元二次方程的問題中少出錯，特把一元二次方程中的易錯題型進行小結，以饗讀者。

一、忽視一元二次方程的二次項系數(shù)不為零

學習方程與函數(shù)類似，務必理解方程與函數(shù)滿足的條件，即二次項系數(shù)不能為零，這是方程首先要滿足的條件，這個條件不滿足，就猶如沒有母雞哪來的雞蛋。

二、確定一元二次方程各項的系數(shù)時，沒有化成一元二次方程的一般形式，導致符號出現(xiàn)錯誤

確定方程各項的系數(shù)，必須把方程化成一般形式，即左邊是關于未知數(shù)的代數(shù)式，右邊是0，最好把二次項系數(shù)化成正整數(shù)，方便后面的計算。

三、不能完全理解用配方法解一元二次方程的原理

要熟練運用配方來解一元二次方程，就必須掌握好配方法的原理。配方法是由完全平方公式推導而來，可改為，讓學生填空，學生容易填b2，可試著問填的常數(shù)與一次項系數(shù)有何關系？如果學生還理解不了，可舉若干實例讓學生理解。

并觀察這四個式子共同的特征，得出添加常數(shù)的結論。當x2項的系數(shù)不是1時，上述結論還成立嗎？要求學生計算下列兩個式子：

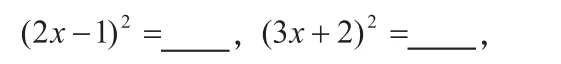
運用配方容易出現(xiàn)的錯誤是：1、二次項系數(shù)不是1時，兩邊除以二次項系數(shù)時出現(xiàn)錯誤；2、兩邊未同時加上所填的常數(shù)項；3、兩邊只是加了一次項系數(shù)的一半；4、所選的完全平方公式出錯，正負不分。

四、運用根與系數(shù)的關系時混淆公式及忽視了Δ≥0

五、混淆實際問題中的單循環(huán)與雙循環(huán)賽制

為讓學生理解好單循環(huán)與雙循環(huán)賽制區(qū)別，可舉例說明：若有四個球隊甲、乙、丙、丁，賽制為單循環(huán)形式（每兩個球隊之間要比賽一場）。對甲來說，甲要與乙、丙、丁各比賽一場，即甲要比賽三場；對乙來說，乙也要與甲、丙、丁各比賽一場，即乙要比賽三場；同理對丙、丁來說也要比賽三場，這樣下來，整個比賽一共比賽了4（4個隊）×3（每個隊均要賽三場）＝12場，但細心的同學會發(fā)現(xiàn)比賽場數(shù)有重復，如甲與乙的比賽只能算一場，按上面的這種算法重復算了一次，所以總的比賽場數(shù)要除以2。

1.（2015·呼倫貝爾）學校要組織足球比賽，賽制為單循環(huán)形式（每兩隊之間賽一場），計劃安排21場比賽，應邀請多少個球隊參賽？設邀請x個球隊參賽，根據(jù)題意，下面所列方程正確的是（ ）

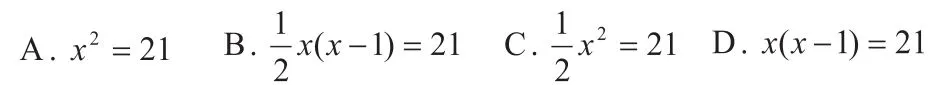
2.某攝影小組互送相片作紀念，已知全組共送出相片132張，則該攝影小組有_______人。