高中數學教師對問題串評價與編制的調查研究

高 翔，張 波

?

高中數學教師對問題串評價與編制的調查研究

高 翔，張 波

（揚州大學數學科學學院，江蘇揚州 225002）

問卷調查表明：新手型教師與經驗型教師對涉及概念命題的探究課問題串設計評價差異不顯著，而對解題或者試卷講評課的評價差異顯著，暴露出新手型教師對于解題、數學知識本身的理解與經驗型教師存在差距；經驗型教師在編制問題串的過程中比新手型教師更加注重激發學生的學習興趣、驅動學生“回歸課本”以及將知識點進行“串聯”；教師對問題串的評價能力與其編制問題串的能力相互影響．

新手型教師；經驗型教師；問題串；評價

1 問題提出

教育家陶行知先生曾經說過“發明千千萬，起點是一問；智者問得巧，愚者問得笨”．可見問題在教學中的地位之重．教師為了推進教學或者指導學生學習，會根據主題，提出一系列的問題，并約定俗成地把這一系列的問題叫做問題串．教師使用問題串進行教學的方法，稱之為“問題串”教學法．以往關于“問題串”教學法的研究，更多的關注了“問題串”本身，包括其理論基礎[1~4]、在教學中如何設置[5]以及如何在某個具體的教學內容下高效使用[6~7]“問題串”教學法，卻鮮有從教師的角度審視“問題串”教學法的研究．那么，新手型教師與經驗型教師對具體“問題串”教學法案例的評價有無差異？新手型教師與經驗型教師問題串編制的側重點是否相同？

2 研究方法

2.1 問卷的編制

在編制調查問卷之前，首先查閱了“問題串”教學法的相關文獻，精心選取了初高中兩個不同課型的“問題串”教學法的案例，先后請一位數學教育研究專家和兩位一線高中數學教師進行審閱．接著，在十位一線的高中數學教師中進行了預測，經過反復修改，最終定稿了“有關‘問題串’教學法的調查（教師問卷）”．

2.2 被試與問卷收發情況

選取100位2014年9月參加在江蘇揚州舉辦的江蘇省高中學科（數學）教師提高培訓的高中數學教師作為被試，他們分別來自揚州、泰州、宿遷和鎮江4個大市．共發放問卷100份，回收85份，其中有效問卷81份，回收率和有效率分別為85%和81%．這81位高中數學教師的基本情況如表1所示．

研究規定教齡在1~5年或者教齡在6~15年且專業技術職稱為中教二級的被試稱為新手型教師；教齡在15年以上或者教齡在6~15年且專業技術職稱為中教一級及以上的被試稱為經驗型教師．據此，回收的有效問卷中，新手型教師有25人，經驗型教師有56人．所占比例分別為30.9%和69.1%．

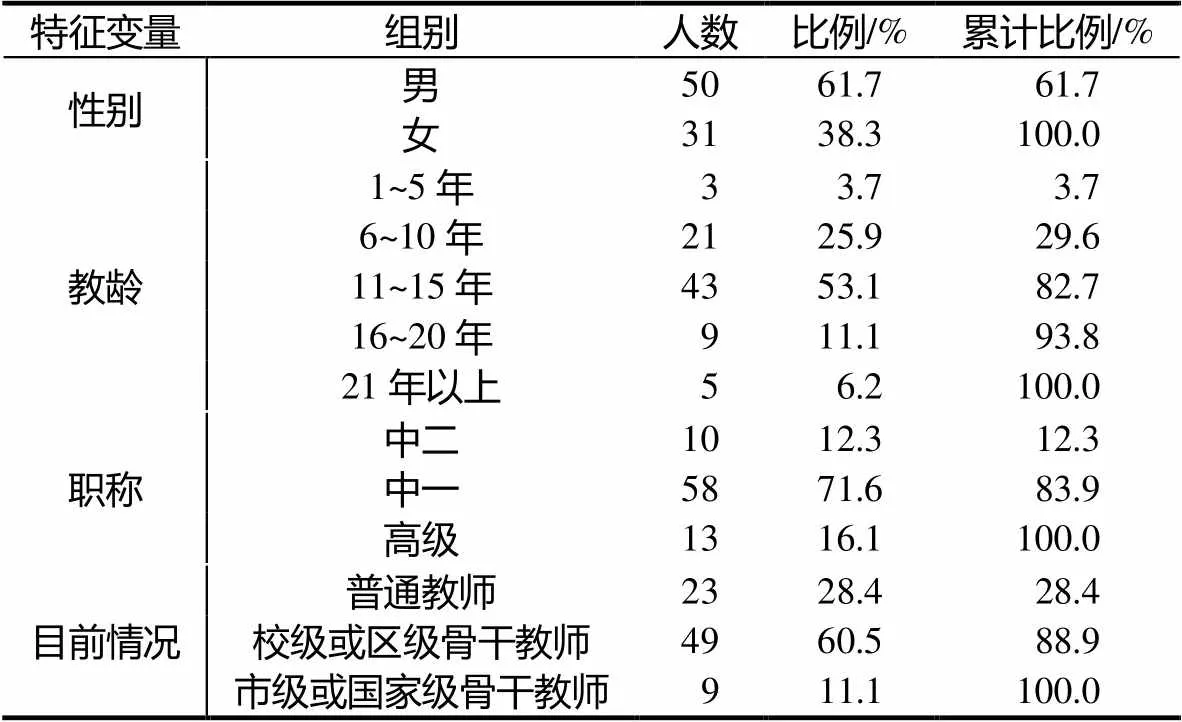
表1 被試基本情況（N=81）

3 結果與分析

3.1 兩種教師對具體“問題串”教學法案例評價的差異

問卷給出了初高中數學教學中的兩個案例，需要教師對案例中的問題串設計進行“好、合格、不好”的評價，并給出理由．其中案例一為同一課題的兩種不同問題串設計，涉及概念和命題的教學以及探究活動；案例二涉及解題和試卷講評的教學．

3.1.1 對案例一的評價

案例一：平行四邊形的性質探索[8]

設計一：

問題一：將一張平行四邊形紙片沿一條對角線剪下，得到兩張三角形紙片，它們能完全重合嗎？它們的邊與角有什么關系？證明你的結論．

問題二：準備兩張形狀、大小完全相同的平行四邊形透明紙片，折出它們的兩條對角線，將它們重合放置在桌面上，并用一枚大頭針固定在對角線交點處，下面的紙片保持不動，將上面的紙片繞著大頭針旋轉180度，觀察它們是否重合．由此你能發現在一個平行四邊形中，還有哪些線段是相等的？證明你的結論．

設計二：

將一張紙對折，剪下兩張疊放的三角形紙片．將它們相等的一組邊重合，得到一個四邊形．

問題一：你拼出了怎樣的四邊形？與同伴交流．

問題二：在拼接得到的平行四邊形中，有哪些相等的線段、相等的角？你是如何得到的？與同伴交流．

問題三：平行四邊形的兩條對角線、相交于點．圖形中有哪些三角形是全等的？有哪些線段是相等的？設法驗證你的猜想．

經過SPSS 21.0的統計分析，得到兩種類型教師對案例一中兩種問題串設計的評價情況如表2、表3所示．

表2 兩種類型教師對問題串設計一的評價

Kolmogorov-Smirnov檢驗結果為=0.344，=1.000>0.05，說明在0.05顯著性水平上新手型教師和經驗型教師對于問題串設計一的評價差異不顯著．

表3 兩種類型教師對問題串設計二的評價

Kolmogorov-Smirnov檢驗結果為=0.716，=0.685>0.05，說明在0.05顯著性水平上新手型教師和經驗型教師對于問題串設計二的評價差異不顯著．針對上述結果，由于新手型教師與經驗型教師的評價差異不顯著，因而研究者將教師對兩種問題串設計的評價較為集中的理由進行了歸類，如表4所示．

表4 案例一兩種問題串設計評價理由表

從表4可以看出，涉及概念、命題的探究活動問題串設計，無論是新手型教師還是經驗型教師均表示應讓學生動手操作、自主探究，從而激發學生興趣、調動學生的思維，讓學生“在數學學習中承擔更大的責任”[9]；在問題串的敘述上，兩類教師認為文字敘述不宜過多，問題的指向性不能太強，即每一個問題指向教師設計好的數學知識與結論，學生完成教師預設的“規定動作”，學生在看似熱鬧的操作中卻沒有得到思維上的提升，很容易產生“滑過現象”[10]，這樣的問題串設計有待商榷；在問題串本身的可操作性上，應盡量降低偏離探究主題的情形，探究活動的結果在很大程度上決定了學生對于新數學知識或結論的“第一印象”，教師應在學生操作的過程中適當加以引導，提高學生探究活動的有效性．

同時，在對案例一的評價中，還意外發現部分新手型教師對于初中學生的數學學習不夠了解，提出了“研究平行四邊形的性質，根本不需要去拼平行四邊形，直接給出定理即可”、“探究活動只適合理解力、觀察力、邏輯推理能力強的學生，差的學生只能看熱鬧”等看法；其次，部分新手型教師不熟悉初中數學教材的編排，如有的教師提出“學生在學習平行四邊形之前還沒有學習過三角形，因此設計二是不符合學生的認知規律的”．

3.1.2 對案例二的評價

案例二：一道習題的講評[11]

教師：所以這道題可以通過什么方法來處理？

學生：數形結合．

學生：斜率為1．

……

學生：用導數．

……

經過統計分析，新手型教師與經驗型教師對于案例二的問題串設計評價如表5所示．

表5 兩種類型教師對案例二的評價

Kolmogorov-Smirnov檢驗結果為=1.791，=0.003<0.05，說明在0.05顯著性水平上新手型教師和經驗型教師對于問題串設計二的評價差異顯著．

整理兩種類型的教師對于案例二評價較為集中的理由，如表6所示．

從表5、表6可以明顯的看出新手型教師和經驗型教師對于案例二的評價有著明顯的分歧．超過半數的新手型教師認為該案例的問題串設計好，問題環環相扣、體現數形結合的思想，激發了學生的思維，少部分新手型教師認為問題取代了學生的思考，跨度不大；經驗型教師則幾乎一針見血地指出該問題串設計思維力度不夠，問題多、敘述啰嗦，沒有揭示該題涉及的數學知識與數學思想等問題．

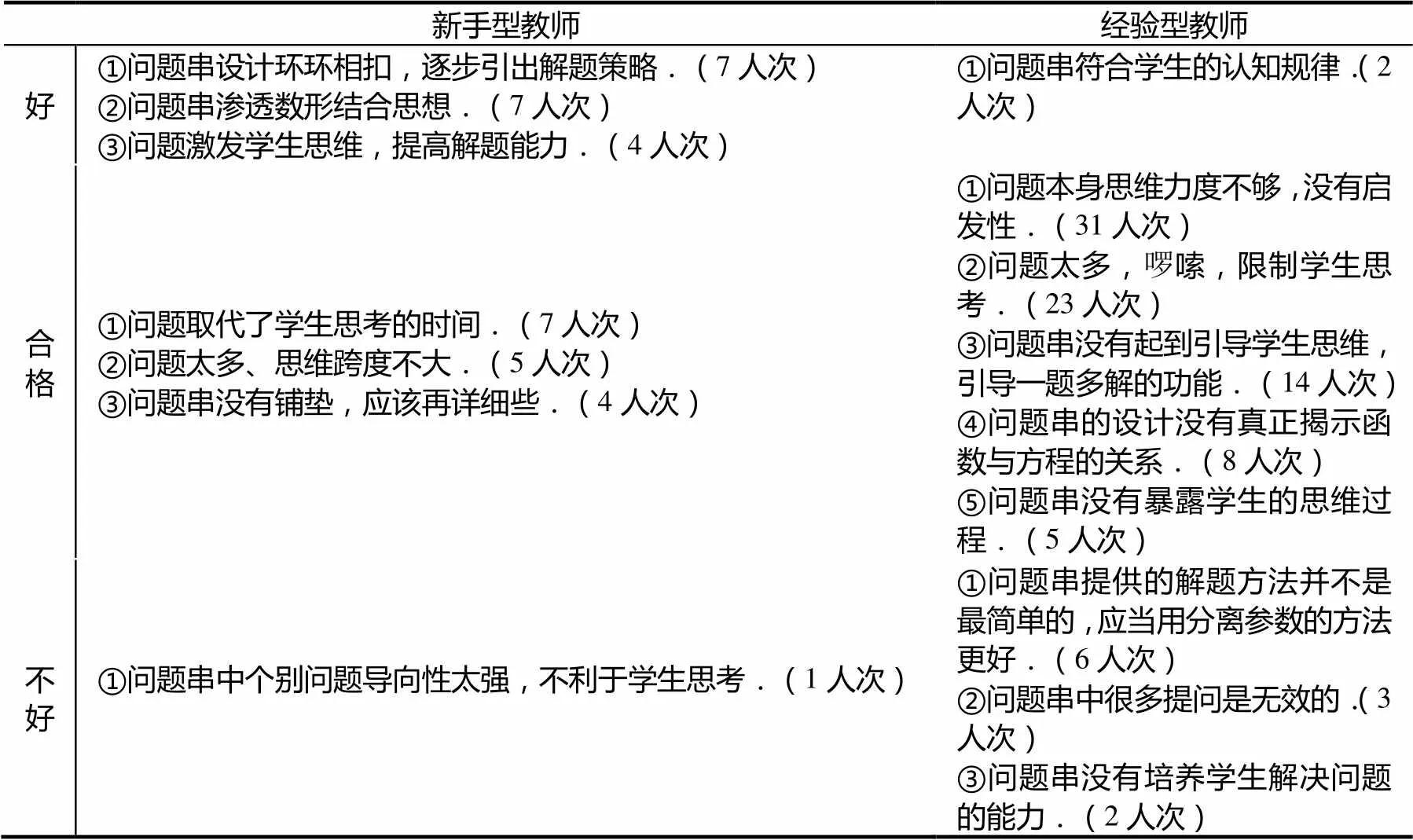
表6 案例二評價理由表

不僅如此，還有近二十位經驗型教師給出了案例二問題串的改進意見．較為集中的幾條如下：意見一，該題較為簡便的方法是分離參數，再引導學生進行數形結合，同時應注意解法的可操作性；意見二，應先讓學生自己分析題目，提出問題，解決問題，若沒思路，教師可以適當提示，再引導學生有無其他解法；意見三，教師應圍繞鼓勵學生說出自己想法、詢問為何想到該法、有無其他方法以及各種解法之間有無優劣之分進行問題串設計．新手型教師中僅有一位教師提出問題串應當引導學生探究函數零點、方程根之間的關系．

3.2 新手型教師與經驗型教師問題串編制的側重點

問卷的最后一個部分要求教師編制“等比數列前項和”的主體部分問題串，并給出編制的理由，該部分調研教師編制問題串的側重點，經過整理得到較為集中的4種問題串設計．

設計一：

引入故事：國王獎勵棋手麥子的故事，棋手要求在第一格放1粒麥子，第二格放2粒麥子，第三格放4粒麥子，以后每一個小格放的麥子是前一格的兩倍，要擺滿64格需要多少粒麥子？

問題四：這種方法的特點是什么？（引出錯位相減）你能仿照上述問題的解法求出一般情形的結果嗎？

問題五：你能仿照上述方法求出更一般的等比數列的前項和嗎？

理由：問題串由數學歷史小故事引入，激發學生的求知欲與興趣；循序漸進，由具體到抽象，由特殊到一般，由易到難，層層遞進，符合學生的認知規律；培養學生猜想解決問題的思路．

設計二：

問題一：你能求

問題二：根據上述求和過程，你有什么發現？

問題三：你能仿照該求和方法，求出

問題四：你能仿照上述方法求出更一般的等比數列的前項和嗎？

理由：遵循從簡單到復雜的原則，讓學生能首先通過各種途經得到結果，逐漸歸納出公式，并能對公式進行有效的思辨．

設計三：

問題二：請參看課本，你有什么方法？

問題三：課本中為什么要乘以一個常數？這個常數是什么？怎么化簡的？

問題四：為什么要討論公比？你能用公式解決嗎？

問題五：請你敘述錯位相減法的步驟及公式使用的注意事項．

理由：讓學生先思考再看書，讓學生進行嘗試，猜想出解題的思路，問題串的設計不能簡單地給學生定下目標，而應起到給學生提供臺階的功能，至于怎樣攀爬，應由學生決定．

設計四：

問題一：等差數列和等比數列的特征量有哪些？

問題三：回顧等比數列的定義，我們將前項和乘上一個公比，你發現與原來的式子有什么聯系？

理由：由復習等差數列的特征量引入，由學生熟悉的知識過渡到陌生的知識，運用類比，符合學生的認知規律．

上述兩種設計的教師人數及比例如表7所示．

表7 兩種類型教師問題串設計人數及比例

如果將以上4種問題串設計稱為“主流的”問題串設計，那么56位經驗型教師中有49位給出了“主流的”問題串設計，占87.5%；而25位新手型教師中僅有11位，比例僅為44%，約為經驗型教師比例的一半．

每一種問題串設計中，經驗型教師的比例均高于新手型教師．由此可以初步推斷出經驗型教師的問題串編制能力要強于新手型教師．

具體看“等比數列前項和”這個內容，課標要求“探索并掌握等差數列、等比數列的通項公式與前項和的公式．”“等差數列和等比數列有著廣泛的應用，教學中應重視通過具體實例（如教育貸款、購房貸款、放射性物質的衰變、人口增長等），使學生理解這兩種數列模型的作用，培養學生從實際問題中抽象出數列模型的能力．”4種問題串設計都較好地貫徹了課標的要求，側重教學的重難點．

在編制問題串的過程中，經驗型教師比新手型教師更加注重：（1）激發學生的學習興趣．設計一中“國王獎勵棋手麥子”的數學歷史小故事，拉近了與學生的距離，提升學習內驅力；設計二中3個簡單的計算式子，貼近學生的“最近發展區”，給學生展示與成功的機會，激發學生的求知欲；（2）驅動學生“回歸課本”．設計三充分體現了教材的重要性，學生并不是不加思考地去教材中找答案，而是在思考了教師給出的問題后，帶著自己的見解去解讀課本，學生會為自己的想法與教材不謀而合而喜悅，也能受到教材的啟發；（3）將知識點進行“串聯”．設計四體現了數學作為一門系統性強的學科，知識點之間相互聯系，很多知識點在整個高中數學知識體系中起著承上啟下的作用，同時側重從學生已經學過的知識引入，過渡十分自然，符合學生的認知規律．

4 調查結論

4.1 兩種類型教師對不同課型的問題串設計評價存在差異

新手型教師與經驗型教師對涉及概念命題的探究課問題串設計（案例一）評價差異不顯著（=0.344，=1.000>0.05；=0.716，=0.685>0.05），但暴露出部分新手型教師不熟悉初中數學知識體系和教材．

新手型教師與經驗型教師對解題或者試卷講評課（案例二）的評價差異顯著（=1.791，=0.003<0.05），暴露出新手型教師對于解題、數學知識本身的理解與經驗型教師存在差異．

與此同時，對案例二的評價與改進中，經驗型教師在解題或者試卷講評課上的表現要優于新手型教師，體現在：（1）追求一題多解，引導學生思辨各種解法之間的差異；（2）教學理念新，倡導學生為主體，教師作為引導者、合作者的教學理念，鼓勵學生表達己見；（3）思考有深度，對于具體的案例，經驗型教師的思考不是停留在問題層面，而是高中數學課程的宏觀視角加以審視，提出的意見一針見血，改進意見中肯有效．

4.2 經驗型教師編制問題串的能力強于新手型教師

在4種“主流”問題串設計中，經驗型教師的比例（87.5%）遠遠高于新手型教師（44%）．4種“主流”的問題串設計體現出了好的問題串標準：緊密圍繞教學內容、適合學生的特點．經驗型教師在編制問題串的過程中比新手型教師更加注重激發學生的學習興趣、驅動學生“回歸課本”以及將知識點進行“串聯”．新手型教師處于模仿與提出問題串的層面上，經驗型教師能夠深入到策略的層面．體現出經驗型教師編制問題串的能力強于新手型教師．

此次調查也體現了一些經驗型教師的教學智慧，如有一位教師在給出“國王獎勵棋手麥子”的例子后，詼諧地問學生：“如果你是國王，你會怎么處理這個尷尬的局面？如果我是國王，我就讓棋手用袋子將麥子裝走，如果裝不走，就不給獎勵．”學生“在數學情境中觀察、分析，產生疑慮、困惑，逐步發現于形成解決數學問題的意識．”[12]

4.3 教師對問題串的評價能力與其編制研究能力相互影響

在對案例二的評價中，許多新手型教師給出了與經驗型教師大相徑庭的評價，認為該問題串的問題環環相扣、體現數形結合的思想，激發了學生的思維．將這7位新手型教師的問卷再次進行了分析，發現7位教師對于案例的評價都是簡單的幾句話：“好，從思想方法上找突破”、“符合學生認知結構”、“問題引入好”……同時還發現有兩位教師在案例一與案例二的評價中至少有一個問題串設計沒有給出評價，有兩位教師沒有給出“等比數列前項和”的問題串設計，在剩下的3位教師中有一位教師給出了“國王獎賞棋手麥子”的設計，其他兩位教師僅僅將問卷中給出的一個問題串設計樣例進行了簡單修改，沒有給出個性化的設計．

以上研究結果在教師實踐層面上也驗證了莊志剛[5]、鄭建元[13]、羅增儒[14]、李渺[15]等人的研究結論．

5 提升新手型教師設計問題串能力的策略

5.1 提高把握數學本質的能力

新手型教師對于不同課型的問題串評價與經驗型教師存在差異，體現新手型教師對于數學本質的把握還不夠．針對不同的課型，新手型教師都應當厘清數學的本質．數學的產生與發展的過程是發現問題、分析問題、解決問題的過程，數學教師的根本任務是還原這個過程，挖掘隱藏在書本知識背后的思想與方法[16]．數學課主要有概念課、原理課和解題課3種課型．

概念課，新手型教師應當認識到數學概念是反映數學對象的本質屬性，既要靜態的分析其定義形式，更需要在比較、變化等聯系活動中揭示其內涵[17]；原理課，應當教會學生了解定理的來龍去脈，積累數學史知識[18]；解題課，應當教會學生如何思考問題，怎樣由已知推向未知，通過變式教學提升學生的思維．

只有針對不同課型，有的放矢地編制問題串，才能從本質上提升新手型教師編制問題串的能力．

5.2 優化問題串設計

經驗型教師在編制問題串時比新手型教師更加注重激發學生的學習興趣、驅動學生“回歸課本”以及將知識點進行“串聯”．從中可以看出，好的問題串應當符合兩大標準．一要緊密圍繞教學內容，二要適合學生的特點．

數學教學本身是將學術形態的數學知識“激活”，轉化為教育形態的知識的過程．新手型教師在進行問題串編制時首先應當宏觀把握數學課程體系、熟知教材內容，然后緊扣教學內容，想方設法地調動學生學習數學的積極性、同時注重對學生思維的訓練，最終提煉出數學思想方法，從而完成一整套的有效教學．

5.3 及時更正設計理念

新手型教師不能對問題串設計案例給出有效的評價，尤其像需要教學經驗積累的解題或者試卷講評課上，新手型教師的想法相比經驗型教師就存在較大差距．同時，部分經驗型教師給出案例二的改進建議，充分體現了經驗型教師問題串設計理念新，思考有深度，這點與左坤[19]、李鵬[20]、徐利[21]、王光明[22]的研究基本吻合．

新手型教師應當主動加強與經驗型教師的溝通交流，虛心聽取經驗型教師的合理化建議，及時更正設計理念．

[1] 曾崢，楊之．“化歸”芻論[J]．數學教育學報，2001，10（4）：38-41．

[2] 陳艷斌，朱維宗，呂傳漢．數學“情境與提出問題”教學與RME教學之比較研究[J]．數學教育學報，2006，15（4）：59-60．

[3] 張奠宙．中國數學雙基教學理論框架[J]．數學教育學報，2006，15（3）：1-2．

[4] Martin A. Simon, Ron Tzur. Explicating the Role of Mathematical Tasks in Conceptual Learning: An Elaboration of the Hypothetical Learning Trajectory[J]., 2004, 6(2): 91-104.

[5] 莊志剛．合理設置激發思維——例談“問題串”在數學教學中的設置[J]．中學數學雜志，2014，（5）：7-9．

[6] 王飛．從一節解析幾何復習課管窺數學問題串教學法[J]．中學數學月刊，2014，（5）：36-37．

[7] 張彥春，李長毅，徐宏偉．職前數學教師教學過程設計的問題與思考——基于“平行線性質”教學過程設計的同課異構個案分析[J]．數學教育學報，2014，23（3）：35-39．

[8] 顧繼玲，張新華．初中數學教材探究活動設計的思考[J]．數學教育學報，2012，21（3）：63-66．

[9] 鄭毓信．“問題解決”與數學教育（2008）[J]．數學教育學報，2009，18（1）：1-4．

[10] 寧連華．數學探究教學設計研究[J]．數學教育學報，2006，15（4）：40．

[11] 王慧清．一道習題講評五種教學設計的辯證思考[J]．中學數學（高中版），2014，（6）：22-24．

[12] 常磊，夏小剛，呂傳漢．數學“情境—問題”教學中教師的MPCK理論研究[J]．數學教育學報，2012，21（5）：67-71．

[13] 鄭建元．初中數學“情境—問題”教學的校本化研究——“用同邊長的正多邊形拼地板”教學案例[J]．數學教育學報，2009，18（1）：99-102．

[14] 羅增儒，羅新兵．作為數學教育任務的數學解題[J]．數學教育學報，2005，14（1）：15．

[15] 李渺，陳長偉．高效數學課堂教學行為研究——基于優秀高中數學教師的個案研究[J]．數學教育學報，2010，19（5）：80-83．

[16] 何勇，曹廣福．數學課堂如何兼顧學生數學素養與應試能力[J]．數學教育學報，2014，23（2）：60．

[17] 李祎．高水平數學教學到底該教什么[J]．數學教育學報，2014，23（6）：32．

[18] 羅新兵，劉陽，安德利亞斯．數學史融入數學教學研究的若干思考[J]．數學教育學報，2012，21（4）：20-23．

[19] 左坤．初中數學教師教學設計能力研究[J]．數學教育學報，2011，20（2）：41-44．

[20] 李鵬，傅贏芳．論數學課堂提問的誤區與對策[J]．數學教育學報，2013，22（4）：97-100．

[21] 徐利．杜郎口模式下的數學課堂教學[J]．數學教育學報，2013，22（2）：99-102．

[22] 王光明．高效數學教學行為的特征[J]．數學教育學報，2011，20（1）：35-38．

Investigation and Study on the Evaluation and Formation of Problem-Chain of High School Mathematics Teachers

GAO Xiang, ZHANG Bo

(College of Mathematics and Science, Yangzhou University, Jiangsu Yangzhou 225002, China)

On the evaluation of designing different types of mathematical classes’ problem-chains, there are obvious differences between novice teachers and experienced teachers in terms of problem-solving or examination paper analysis. However, not clear in the concept of teaching. The experienced teachers are better than novice teachers in problem solving and mathematics knowledge understanding. Experienced teachers pay more attention to designing problem-chains, such as breaking through the important and difficult points in teaching, making knowledge “series”, stimulating students’ interests in learning and driving students to “return of textbooks” etc. At the same time, there is an interrelationship between teacher’s evaluation and formation ability of problem-chains.

novice teachers; experienced teachers; problem-chain; evaluation

[責任編校：陳雋]

G633

A

1004–9894（2016）03–0066–05

2016–01–09

中國學位與研究生教育學會課題——密西根州立大學教育碩士培養的案例研究（B2-2013Y09-137）

高翔（1990—），男，江蘇金壇人，碩士生，主要從事數學教育研究．