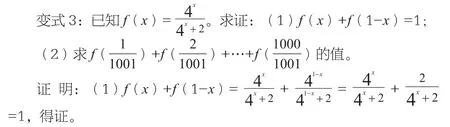變式教學在高中數學課堂教學中的應用

江蘇省鹽城市第一中學 張 軍

變式教學在高中數學課堂教學中的應用

江蘇省鹽城市第一中學 張 軍

變式教學，主要是指在保持事物本質特征不變的情況下，通過從不同角度、方位、背景等方面，有目的、有針對性地對數學概念、公式、定理、習題等進行變換，從而引導學生從“變”的現象中挖掘和把握“不變”的內在規律和本質屬性，培養學生靈活多變的思維能力。在高中數學教學中，教師要立足教學實際需要，優選有效策略，靈活巧妙地開展變式教學，從而發散學生思維，提高教學效果，促進學生的有效發展。對此，筆者結合教學實踐，就變式教學在高中數學課堂教學中的應用提出一些建議，以供參考。

一、引入變式，創設情境，激發動機

引入變式，即在新課導入環節通過引入直觀、生動或具體的變式問題引出新課學習內容，激發學生的探究熱情。在高中數學中，教師應注意結合學生的心理特點和認知發展規律，圍繞教學目標，從學生已有知識和生活經驗出發，靈活巧妙地引入變式，創設富有挑戰性和探索性的問題情境，布疑設坎，制造矛盾沖突，從而激起學生思維的漣漪，激發學生探究動機，調動學生參與新課學習的積極性和主動性。

案例1：教學“線面垂直的判定定理”時，考慮到所學的知識較為抽象，為了加深學生對知識有更加直觀形象的理解，筆者引入了如下的變式情境。

變式1：如圖1所示，將一本書直立在桌子上，書脊所在的直線與桌面有著怎樣的位置關系？無論打開的程度如何，是否都能保證其書脊所在的直線與桌面垂直？

變式2：如圖2所示，取一張A4紙，將其剪成一個三角形ABC，沿一個頂點將三角形進行折疊，得到折線AD，接著再將折疊后的紙豎起放置在桌子上，請問折線AD是否會與桌面垂直？怎樣折疊才能確保折線AD與桌面所在平面垂直？

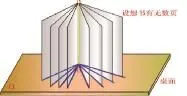
圖1

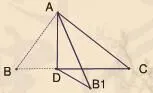
圖2

學生通過積極思考、觀察探索、動手實踐、獨立完成實驗，不難發現：

（1）無論書打開的程度有多大，其書脊與紙的底部始終在桌子上，且書脊與紙的底部是垂直的；

（2）當且僅當AD⊥BC時，AD所在直線與桌面所在平面垂直，而折疊后其垂直關系保持不變，即AD⊥CD，AD⊥BD。

最后，經過歸納總結，得出了這樣一個結論：若一條直線與平面內的兩條相交直線都垂直，則該直線與此平面垂直。這樣，通過引入變式，創設問題情境，既有效地引出了課題，集中了學生的注意力，激發了學生探究熱情，又觸發了學生思維，訓練了學生思考、分析和解決問題的能力。

二、概念變式，深入剖析，把握本質

數學概念是對客觀現實中對研究對象數量關系、空間形式或結構關系的本質特征的高度概括。巧妙地進行概念變式，有助于幫助學生深化概念理解，把握概念本質屬性，優化思維過程，完善學生的認知結構。在高中數學教學中，當學生學習完某個數學概念后，教師可以針對該概念的內涵和外延，精心設計辨析型變式問題，因勢利導，啟發學生積極思考、剖析、比較，促進其悟，從而激活學生思維，把握概念本質特征，促使學生的認知結構更加系統化和全面化。

案例2：講解“異面直線的概念”時，筆者設置了如下變式判斷問題，以引導學生完整地建構異面直線概念，把握其本質內涵和屬性。

（1）平面內的一條直線和平面外的一條直線是異面直線；

（2）分別在兩個不同平面內的兩條直線是異面直線；

（3）空間中既不相交也不平行的兩條直線是異面直線；

（4）不同任何一個平面內的兩條直線是異面直線；

（5）不在同一平面內的兩條直線是異面直線。

這樣，通過概念變式，辨析判斷，深化了學生概念理解和把握，明確了概念本質，引發了學生頭腦中固有思維模式的沖突，點燃了學生的思維之火。

三、習題變式，強化鞏固，拓寬思維

習題是強化鞏固知識、開發智力、提升學習能力的有效手段，進行習題變式，有助于訓練學生的思維積極性、敏捷性、靈活性以及變通性，開闊學生知識視野，培養學生全方位思考、分析和處理問題的能力，提升學生的解題效率。在高中數學變式教學中，教師可以適當地變式習題，發散學生思維，拓寬學生的解題思路，引導學生多向思考、分析和解決問題，學會舉一反三、觸類旁通，從而夯實數學知識，培養學生良好的思維品質，提升學生探究、創新和解題能力。

案例3：教學了“函數的對稱性”后，筆者設計了以下的變式習題。

變式1：已知函數y=f（x）滿足f（-x+1）=f（x+1），

求證函數y=f（x）的圖象關于（1,0）對稱。

證明：∵f（-x+1）=f（x+1），∴y=f（x+1）為奇函數，

∴y=f（x+1）的圖象關于（0，0）對稱，

故y=f（x）的圖象關于（1，0）對稱。

變式2：已知函數y=f（x）滿足f（x）+f（2+x）=2，求證y=f（x）的圖象關于（1,1）對稱。

證明：令x=a-1，則-x=1-a，∵f（x）+f（2+x）=2，∴f（1+a）+f（1-a）=2，∴f（x）滿足f（1+x）+f（1-x）=2，

即f（-x+1）-1=-[f（x+1）-1]，

∴y=f（x+1）-1的圖象關于原點（0，0）對稱。

故y=f（x）的圖象關于（1，1）對稱。