反比例函數最值問題解題方法分析
江蘇省南京市玄武外國語學校 沈 艷
反比例函數最值問題解題方法分析
江蘇省南京市玄武外國語學校 沈 艷
反比例函數的最值問題由于其強大的兼容性,可以結合多種函數知識,能更好地考查學生綜合運用數學知識的能力以及對數學思想方法的掌握情況,成為了近年來中考的熱門題型。本文針對不同的最值情況提出不同的解題方法,以供學生復習參考。
最值問題;反比例函數;綜合應用
本文從線段最值,周長最值,面積最值三個角度依次舉例說明與反比例函數相關的最值問題的解法,數形結合思想、方程思想等數學思想在此過程中有著重要的應用。
一、三角形性質法
巧妙構造三角形,利用三角形中兩邊之和大于第三邊以及兩邊之差小于第三邊的性質,可以判斷出線段和或差的最值問題。
解析:先利用點的坐標求出函數中的未知量,再結合三角形各邊的關系找出最小值。將A點坐標分別代入y1、y2求得k=-2/3,m=-12。
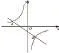
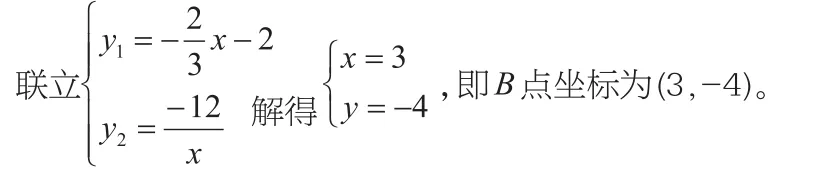
當PA,PB與AB構成一個三角形時,由三角形三邊關系可知|PA+PB|>|AB|恒成立,故當且僅當P在AB上時,|PA+PB|最小,且等于。
點撥:本題中通過三角形解題,不需要分別列式計算PA、PB的長,使問題由繁化簡,節省了很大的計算量,是數形結合思想的完美體現。
二、配方法
配方法就是將關系式配成二次函數或者三次函數的形式,再利用相關知識解答,在解題時出現不在課本上介紹過的初等函數范圍內時,常用配方法解決。
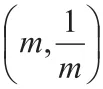
OABC的周長,然后利用配方法求最小值。
AC=m,AB=,因為AB⊥x軸和AC⊥y軸,OC⊥OB,所以四邊形OBAC為矩形,故其周長為:
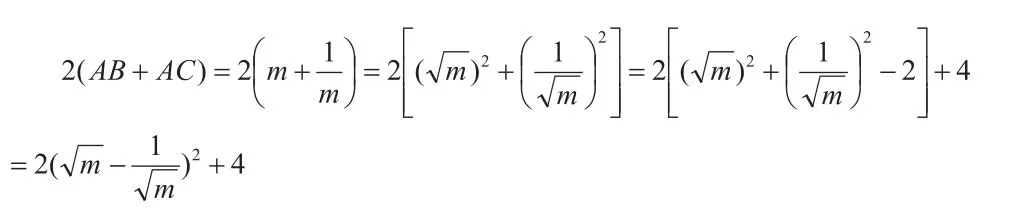
點撥:本題用四邊形周長代數式的特點列出的函數式是中學階段較為常見的也是很重要的關系式,利用配方法解此式是學生應該掌握的解題能力。
三、二次函數法
將數量關系表達為二次函數,根據其函數性質就可以很直接地看出最值的有無以及大小了,此法多見于求多邊形周長或者面積的最值問題。下面例題中為面積最值。
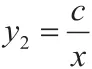
解析:將點B的坐標代入,解得c=-5,則,將點的坐標代入y2,得d=-2,則,而一次函數y1=kx+b的圖象經過B(-1,5)、兩點,故。令y1=0,解得x=3/2,故,由題意,設,因為DP∥x軸,且點D在y2的圖象上,故,即。則△PAD的面積為。又n=-2m+3, -1<m<3/2,得0<n<5,而,故當時,即時,△PAD的面積S最大,為。
點撥:本題在反比例函數的知識點上又綜合考査了一次函數的解法、二次函數的解法等初中的核心內容,在能力上檢驗了學生在動態情形下對圖形的觀察分析能力及函數知識的綜合應用能力。
從本文的舉例中可以看出,反比例函數最值問題應用的數學方法多,縱橫聯系復雜,注重數學思想的運用,希望在提升學生解此類問題能力的同時可以激發學生的探索興趣,塑造自身的思維品質。

