借動量守恒之道,破碰撞問題謎團
許志剛●
江蘇省如皋市第一中學(226500)
借動量守恒之道,破碰撞問題謎團
許志剛●
江蘇省如皋市第一中學(226500)
動量守恒定律是自然界中最普遍的定律,雖說其源于牛頓定律,但是其適用性比牛頓定律還要廣泛,在高考中也是必不可少的內容.碰撞問題由于其涉及到動量與能量等多方面的相關知識,對于學生的綜合解題能力存在有效的檢驗,故成為高考的熱點題型.
彈性;非彈性;完全非彈性;動量守恒
在高中的學習中遇到的問題,由于碰撞過程中相互作用時間極短相互作用力又極大,故可忽略系統所受的外力,進而認為只有內力相互作用,滿足動量守恒的條件.本文中針對三種不同的碰撞情況分別舉例分析作答,讓學生更好的體會動量守恒定律的應用.
一、彈性碰撞
又被稱為完全彈性碰撞,即物體之間發生碰撞時,不存在機械能的損失,只是通過彈力做功使機械能在兩物體間轉移,碰撞前后物體的動量以及系統的機械能均守恒.列式關系為碰撞前后動量守恒,動能不變.
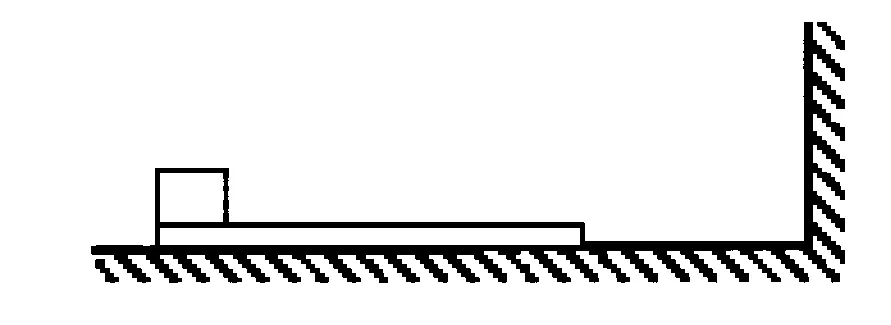
圖1
例 如圖1所示,有一木板左端放有一重物在光滑的水平地面上,其右方有一豎直的墻.木板質量為重物質量的1/2,重物與木板間的動摩擦因數為μ,若木板與重物速度v0共同向右運動,某時刻木板與墻發生碰撞時間極短的彈性碰撞.求木板從第一次與墻碰撞到再次碰撞所經歷的時間.(設木板足夠長,重力加速度為g)
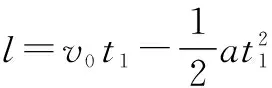
本題中的技巧性在于應用動量守恒定律求出兩者達到的共同速度的大小及方向,省略了復雜的中間過程,若是運用運動學中的式子進行計算會極大地增加計算量.充分利用彈性碰撞中速度大小不變這一規律可以幫助我們快速解題.
二、完全非彈性碰撞
從能量的角度進行分析是機械能不守恒,且機械能損失最大,但動量守恒.對應此種情況的就是碰撞后碰撞物體粘在一起具有共同速度,將此過程中損失的機械能轉化為物體內能.我們要借助動量守恒這一點求得碰撞后的共同速度,進而解題.
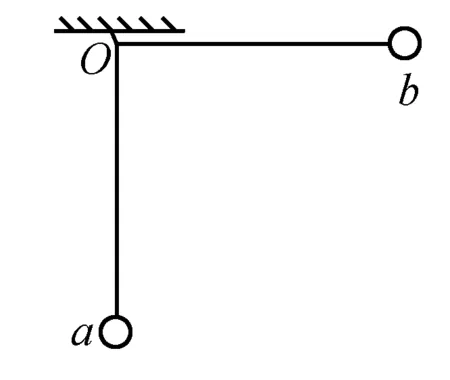
圖2
例 如圖2所示,點O處用等長的細線懸掛小球a、b.現讓球a靜止下垂,將球b向右拉至細線水平.后靜止釋放球b且兩球碰后粘在一起向左擺動至細線與豎直方向為60°的最大偏角處.此過程忽略空氣阻力,求(1)a、b兩球的質量之比(2)兩球在碰撞過程中損失的機械能與碰前b的最大動能之比.(設重力加速度為g)
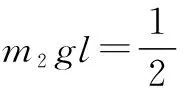
本題中對于能量的考察是創新之處,通過動量問題與能量問題的綜合檢驗使本題更具邏輯性以及趣味性,在此類碰撞問題中必然存在能量的轉換,學生必須全面掌握物理學知識才能更好的應對多變的題型,形成更為完善的解題思路.
三、非彈性碰撞
把這種情況放在最后說明,原因是從能量的角度來看其處在上述介紹的兩種情況之間,即在碰撞過程中使部分機械能裝化為內能,但系統的動量仍然守恒,針對此種情況,常出現要求對碰撞物的質量、碰撞后的速度等值進行范圍的計算.
例 質量為1kg的小球以4m/s的速度與質量為2kg的靜止小球發生非彈性碰撞,則關于碰后兩球的速度v1′與v2′的取值范圍是____.
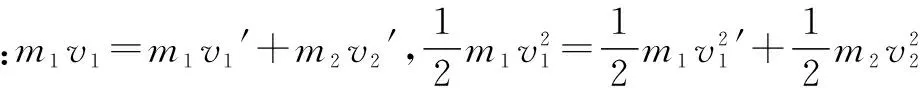
任何一種碰撞,必介于彈性碰撞與完全非彈性碰撞之間,我們只要牢記這一點,對于此類問題的求解就很簡便了,本題就是借此進行對問題的分析求解.
碰撞的情況只有這三種,對于不同情況下動量守恒的運用需要選對物體以及碰撞后的運動狀態,選取的對象不同必然導致所列的方程不同.靈活的運用動量守恒可以使我們的解題思路更為清晰,計算量大為減小,在碰撞問題的海洋中任意遨游.
G632
B
1008-0333(2016)34-0068-01

