預制空心方樁抗彎承載力研究

王清龍，楊德健

(1. 天津城建大學，天津 300384；2. 天津建城基業集團有限公司，天津 300301)

預制空心方樁抗彎承載力研究

王清龍1,2，楊德健1

(1. 天津城建大學，天津 300384；2. 天津建城基業集團有限公司，天津 300301)

通常的混凝土受彎承載力計算均采用混凝土屈服模型．本文對預制空心方樁抗彎承載力計算采用鋼筋屈服模型．在該模型基礎上，推導出預制空心方樁抗彎承載力計算公式．通過對比兩種計算結果表明：在構件配筋率高的情況下，按混凝土屈服模型更符合實際又偏于安全；在構件配筋率低的情況下，按鋼筋屈服模型更符合實際且偏于安全．

預制空心方樁；抗彎承載力；配筋率

預制空心方樁包括先張法預應力離心混凝土空心方樁(以下簡稱預應力方樁)和預制鋼筋混凝土空心方樁(以下簡稱空心方樁)．近年來，預制空心方樁在工程中的應用越來越多，對其研究也日益增多．國內外學者對打樁過程中的力學機理以及多種因素下對打樁破壞的影響做了詳細的研究[1-3]；李志剛、劉永超等[4-5]研究了預制樁的工程應用；劉金皊等[6]研究了預制樁沉樁可行性分析實用方法；張忠苗等[7]對管樁和預制方樁的豎向承載力進行了對比分析；還有學者對其抗震進行了研究[8-9]．但這些研究都是樁與地基土相結合、彼此相互作用的研究，而對樁自身的抗彎承載力的研究則沒有涉及．

王廣宇[10]和繆海林[11]研究了預應力方樁抗彎承載力的計算，王廣宇在計算預應力方樁抗彎承載力中做了幾點假定，其中包括“假定受壓區預應力鋼筋不參與抗彎，假定受拉區鋼筋全部達到屈服”．筆者并沒有做這樣的假定，而是讓所有的鋼筋均參與抗彎承載力的計算，同時認為在中和軸附近的鋼筋是沒有達到屈服強度的，這一觀點和繆海林的觀點是一致的．從繆海林給出的預應力方樁抗彎承載力的計算公式可知，他從混凝土屈服的角度出發計算其抗彎承載力．筆者認為根據配筋的不同，混凝土和鋼筋均有可能先屈服，甚至王廣宇認為對預應力方樁壓區混凝土的破壞幾乎沒有，從而說明了考慮鋼筋屈服來計算預制空心方樁抗彎承載力的必要性．

1 從鋼筋角度計算預制空心方樁抗彎承載力

1.1 第i排鋼筋的應力值σpi的計算

預制空心方樁抗彎承載力的計算不同于一般梁截面抗彎承載力的計算．因為梁截面一般都是上下配筋，而預制空心方樁則是四面均勻配筋，具體見圖1-2．

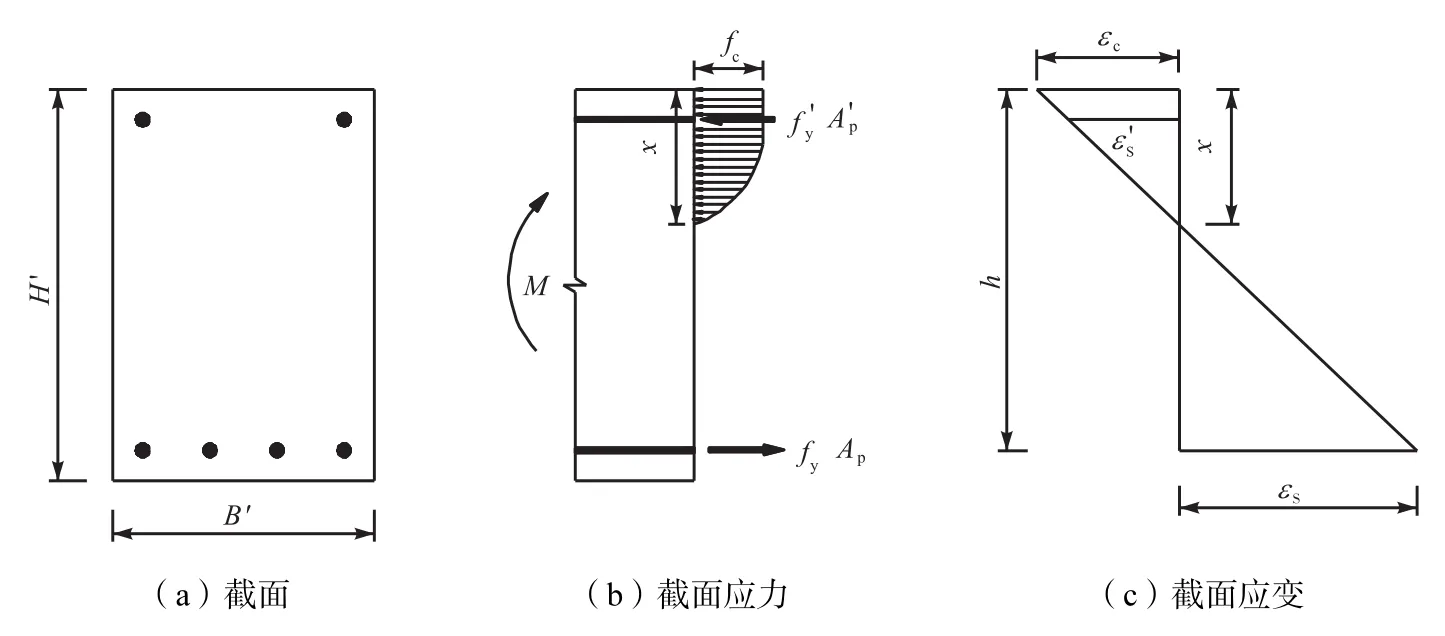
圖1 梁截面計算示意

圖2 空心方樁截面計算示意

第i排鋼筋的應力值σpi，可根據GB50010—2010《混凝土結構設計規范》[12]中相應公式計算，但此計算公式是建立在受壓區邊緣纖維的應變達到混凝土的極限壓應變，再根據平截面假定，利用相似三角形求出σpi．

為了從鋼筋屈服角度計算預制空心方樁抗彎承載力，必須求出從鋼筋屈服角度推導出的第i排鋼筋的應力值σpi的計算公式，即已知εs1，求εc、 εsi(i＝2，…，n)．這也是本文對計算預制空心方樁抗彎承載力的貢獻之一．根據文獻[12]規定，縱向鋼筋的極限拉應變取為0.01，即εs1=0.01．仍根據平截面假定，利用相似三角形求得普通鋼筋應力

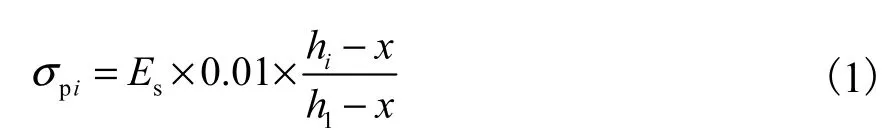
式中：Es為鋼筋彈性模量；hi為第i層縱向鋼筋截面重心至截面受壓邊緣的距離；h1為最外排鋼筋截面重心至截面受壓邊緣的距離；x為混凝土受壓區高度．

1.2 相關參數之間的關系

研究抗彎承載力，首先要確定混凝土受壓應力與應變的關系．文獻[12]中采用拋物線上升段和水平段的混凝土受壓應力-應變關系曲線，見圖3[13]．

圖3 混凝土應力-應變曲線

為了計算抗彎承載力，需要確定幾個臨界值．按文獻[12]規定，縱向鋼筋極限拉應變取為0.01．根據平截面假定和相似三角形，可求出相應受壓區高度與混凝土壓應變臨界值的關系．

圖4 x1計算示意

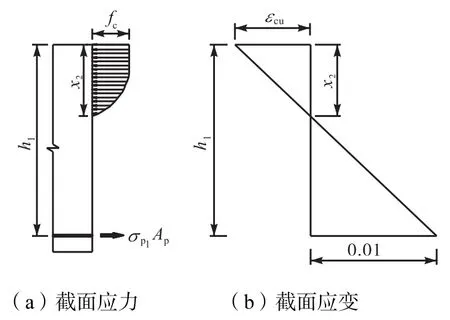
圖5 x2計算示意

圖6 x3計算示意

應變為ε0時，對應的該點距中和軸的距離，計算示意如圖7所示．

1.3 抗彎承載力計算公式

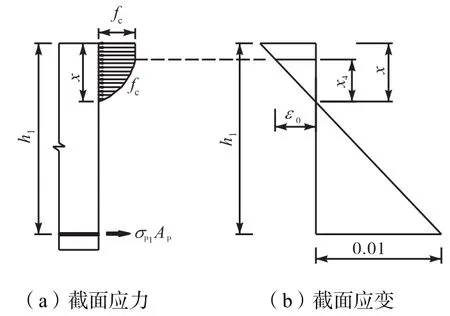
圖7 x4計算示意

從鋼筋屈服角度計算預制空心方樁抗彎承載力時，因為并不知道混凝土是否破壞，所以不能用等效矩形應力的方法求受壓區混凝土所受壓力，只能用積分的方法求混凝土所受壓力以及受壓區混凝土合力作用位置距中和軸的距離yc．

(1)混凝土受壓區高度x小于等于受壓區翼緣高度hf′(即x≤hf′)．

當0＜x≤x1時，即受壓區混凝土應力位于圖3所示OA段，由受彎構件正截面力的平衡得：

式中：B為預制空心方樁的邊長，y為受壓區混凝土任意一點距中和軸的距離．由式(3)求得混凝土受壓區高度x，受壓區混凝土合力作用位置距中和軸的距離為

抗彎承載力

當x1＜x≤x2時，即受壓區混凝土應力位于圖3所示OAB段，由受彎構件正截面力的平衡得：

由式(6)求得混凝土受壓區高度x，受壓區混凝土合力作用位置距中和軸的距離為

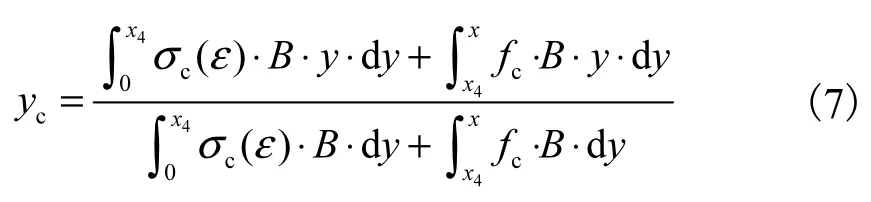
抗彎承載力按公式(5)計算．

(2)混凝土受壓區高度x大于受壓區翼緣高度hf′(即x＞hf′)．

當0＜x≤x1時，即受壓區混凝土應力位于圖3所示OA段，由受彎構件正截面力的平衡得：

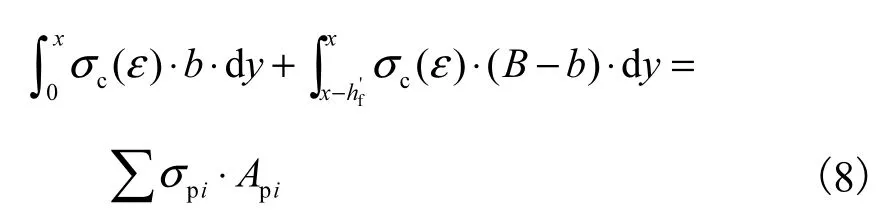
式中：B為預制空心方樁的邊長；b為空心方樁截面換算成等截面、等慣性矩的I型截面的腹板寬度；y為受壓區混凝土任意一點距中和軸的距離．由式(8)求得混凝土受壓區高度x，受壓區混凝土合力作用位置距中和軸的距離為

抗彎承載力按公式(5)計算．

馳騰科技有限公司董事長詹友林對《中國經濟周刊》表示：“中國是全世界獨一無二的全方位智能手機市場，但還有很多國家通信比較落后，中低端、功能機的市場還很大。現在電子行業開始向西部轉移，我們來瀘州，一是因為瀘州在政策上大力支持，比如廠房三年免租，登記辦證一對一服務，后期保障到位。二是因為勞動力市場大，員工在這里生活更經濟、也更安心。”

當x1＜x≤x2，且x≤x3時，即受壓區混凝土應力位于圖3所示OAB段，此時受壓區翼緣處混凝土應力部分位于OA段，部分位于AB段，由受彎構件正截面力的平衡得：

由式(10)求得混凝土受壓區高度x，受壓區混凝土合力作用位置距中和軸的距離為

抗彎承載力按公式(5)計算．

當x1＜x≤x2，且x＞x3時，即受壓區混凝土應力位于圖3所示OAB段，此時受壓區翼緣處混凝土應力均位于AB段，由受彎構件正截面力的平衡得：

由式(12)求得混凝土受壓區高度x，受壓區混凝土合力作用位置距中和軸的距離為

抗彎承載力按公式(5)計算．

應當說明，當求得的混凝土受壓區高度x＞x2時，表明該構件配筋太多，為超筋破壞，本公式不適用．

2 兩種方法計算結果的對比分析

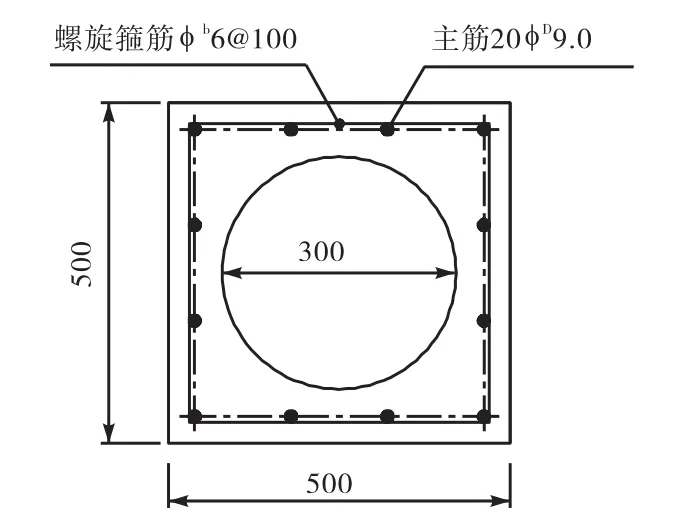
圖8 Z1配筋

圖9 Z2配筋

對空心方樁Z1、Z2分別從混凝土屈服和鋼筋屈服兩種不同破壞模型計算其抗彎承載力，計算結果詳見表1-2．

表1 Z1抗彎承載力統計表

表2 Z2抗彎承載力統計表

從表1可以看出：Z1采用混凝土屈服模型計算的抗彎承載力比采用鋼筋屈服模型計算的抗彎承載力大．這是因為Z1的配筋率僅為0.43%,，配筋率很低，因此空心方樁在受彎過程中，混凝土并沒有完全發揮作用，而鋼筋卻完全發揮了作用．故采用混凝土屈服模型，即混凝土能夠充分發揮作用的模型，由于過多考慮混凝土的作用，從而導致其計算結果會偏大一些．

從表2可以看出：Z2采用鋼筋屈服模型計算的抗彎承載力比采用混凝土屈服模型計算的抗彎承載力大．這是因為Z2的配筋率為1.83%,，配筋率很高，因此空心方樁在受彎過程中，鋼筋并沒有完全發揮作用，而混凝土卻完全發揮了作用，故采用鋼筋屈服模型，即鋼筋能夠充分發揮作用的模型，由于過多考慮鋼筋的作用，從而導致其計算結果偏大．

綜上所述，樁的配筋率的大小決定了哪種計算模型比較準確，但這個配筋率并沒有一個定值，因此在計算預制空心方樁抗彎承載力時，宜采用兩種模型分別計算，取其較小值，這樣即偏于安全，又符合實際的破壞形態．

3 結 論

(1)本文建議性地給出了從鋼筋屈服的角度，計算第i排鋼筋的應力值σpi的公式以及計算預制空心方樁抗彎承載力的公式；

(2)在計算預制空心方樁抗彎承載力時，宜采用混凝土屈服模型和鋼筋屈服模型分別計算，取其較小值，這樣的計算結果既偏于安全，又符合實際的破壞形態；

(3)按鋼筋屈服模型計算預制空心方樁抗彎承載力，是對計算預制空心方樁抗彎承載力方法的一種豐富和發展，它使得預制空心方樁抗彎承載力的計算更全面，從而更好地為預制空心方樁在工程中的應用發展提供更可靠的技術支持．

［1］ 劉屠梅. 基樁檢測技術與實例[M]. 北京：中國建筑工業出版社，2006.

［2］ RAUSCHE F，GOBLE G G，LIKINS G. Dynamic determination of pile capacity[J]. J Geotech Eng，1985，111(3)：367-383.

［3］ 張亞南，馮 春，李世海，等. 混凝土預制樁在沖擊荷載作用下的破壞機理研究[J]. 建筑結構，2013(增刊1)：876-881.

［4］ 李志剛，張雁朱，合 華，等. 預應力高強空心樁(管樁和方樁)工程應用分析[J]. 建筑結構，2014(8)：1-5.

［5］ 劉永超，朱明亮，王清龍，等. 預應力矩形支護樁在濱海軟土深基坑工程中的應用研究[J]. 土木工程學報，2015(增刊1)：168-173.

［6］ 劉金皊，張益凡，李 娜，等. 預制樁沉樁可行性分析實用方法[J]. 建筑結構，2013(11)：92-97.

［7］ 張忠苗，喻 君，張廣興，等. PHC管樁和預制方樁受力性狀試驗對比分析[J]. 巖土力學，2008(11)：3,059-3,065.

［8］ 劉陜南，高承勇，侯勝男，等. 上海地區建筑樁基水平抗震設計初步探討[J]. 建筑結構，2013(7)：88-93.

［9］ 倪國泉，楊 軍，潘 鵬，等. 預應力混凝土空心方樁承臺節點抗震性能試驗研究[J]. 地震工程學報，2013(2)：246-251.

［10］ 王廣宇. 預應力混凝土空心方樁成套技術研究[D]. 北京：中國科學建筑研究院，2007：86-88.

［11］ 繆海林. 江蘇省空心方樁圖集新舊版本內容差異分析[J]. 江蘇建筑，2013(1)：93-106.

［12］ 中華人民共和國住房和城鄉建設部. 混凝土結構設計規范：GB50010—2010[S]. 北京：中國建筑工業出版社，2010：34-40.

［13］ 王鐵成. 混凝土結構原理[M]. 天津：天津大學出版社，2002：56-61.

Research of Flexural Capacity of Precast Hollow Square Piles

WANG Qinglong1,2，YANG Dejian1
(1. Tianjin Chengjian University，Tianjin 300384，China；2. Tianjin City Construction Group Co.，Ltd，Tianjin 300301，China)

Usually the concrete yield model is used to calculate concrete flexural bearing capacity. In this paper,the steel yield model is used to calculate the bearing capacity of precast hollow square pile. On the model basis，the calculation formula of bearing capacity of precast hollow square pile is derived. According to the comparision,a conclusion indicates that the concrete yield model is real and safe when reinforcement ratio of precast hollow square pile is big；meanwhile，the steel yield model is real and safe when reinforcement ratio of precast hollow square pile is small.

precast hollow square piles；flexural bearing capacity；reinforcement ratio

TU473.1

A

2095-719X(2016)06-0427-05

2015-11-06；

2016-03-08

王清龍（1983—），男，河北滄州人，天津建城基業集團有限公司工程師，天津城建大學碩士生．