高中三角函數內容深度的實證研究——基于大學數學專業(yè)的學習

佘 丹

?

高中三角函數內容深度的實證研究——基于大學數學專業(yè)的學習

佘 丹

（南京師范大學，江蘇南京 210097）

基于大學數學專業(yè)的學習，從課程標準、高考命題、大學生數學水平3個方面對高中三角函數內容深度進行定量分析和定性分析．三角函數的定義、三角公式的靈活運用未達到大學要求的水平，而課程標準刪除的積化和差、和差化積公式、萬能公式、余切函數等在大學數學專業(yè)學習中有著重要作用．

課程標準；高考命題；大學生；三角函數

1 研究背景

目前較多大學數學專業(yè)學生因對中學的一些基礎知識不熟悉，上課出現(xiàn)聽不懂或反應遲緩的現(xiàn)象，使得教師需花時間去講中學知識，影響了課堂成效[1~4]．因為此，基于大學數學專業(yè)的學習，研究高中三角函數內容深度能對課程建設提供一定建設性的參考．包括課程標準（以下簡稱標準）、高考命題、大學生數學水平3個方面三角函數內容深度的研究，結合調查做初步探討．

2 研究概況

2.1 教材的選擇

高中三角函數內容以人教A版教材為標準，大學數學專業(yè)三角函數相關內容以華東師范大學數學系編寫的數學分析教材為標準．

2.2 研究的內容與方法

2.2.1 標準中三角函數內容深度研究的內容與方法

知識的深度指對知識的掌握程度，標準中的目標包括3個方面：知識與技能，過程與方法，情感、態(tài)度、價值觀，其中前兩方面都可用來刻畫對知識要求的深度，稱為結果性目標和過程性目標．參考布魯姆認知水平，按標準中的分層[5]，對結果性目標分為3個水平，分別賦值1、2、3，過程性目標分為兩個水平，分別賦值1、2，具體規(guī)定見表1[8]．

表1 課程目標動詞賦值

對每個知識點采用累加法對其深度賦值，以該值作為該知識點的深度．例如，“根據具體函數的圖象，能夠借助計算器用二分法求相應方程的近似解，了解這種方法是求方程近似解的常用方法”采用累加法賦值為1+2+1=4．標準對目標的描述分為兩類：一類是要求在經歷某個過程后，認知某個數學知識；另一類是要求通過實例或操作認知某個數學知識．不管是經歷過程還是通過操作都是對知識的深度有更高要求，因此這種累加賦值是合理的．

2.2.2 高考命題三角函數內容深度研究的內容與方法

以全國自主命題的16個省市近3年的高考題（均為新課標卷）為研究對象（四川、重慶兩省2010年才進入課改，對這兩省的高考題只選取2013、2014年研究），選出其中涉及三角函數的題目，根據SOLO理論評價試題設置的難易程度．表2是根據SOLO分類評價理論將觀察到的學習結果分成5個層次水平[6]，這5種結構水平代表學生思維發(fā)展的5個階段，反映了試題編制所對應的5個水平．下文用0-水平、1-水平、2-水平、3-水平、4-水平，分別對應前結構水平、單一結構水平、多元結構水平、關聯(lián)結構水平、擴展抽象水平．依據SOLO理論對每個知識點不同水平的界定標準，判斷該題所涉及的知識點及所考查的水平，若一道題考查了多個知識點，則在每個知識點下均算一題．SOLO理論的各個水平及其表現(xiàn)見表2[6]．

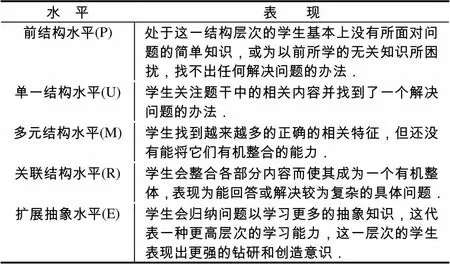
表2 SOLO理論的各個水平及其表現(xiàn)

2.2.3 大學數學專業(yè)學生三角函數知識深度研究的內容與方法

訪談某師范大學（省屬一類院校）數學系教數學分析的教師，以了解數學專業(yè)大學生的學習現(xiàn)狀，根據訪談結果，設計調查問卷，在福建省一所重點大學數學專業(yè)大一、大二、大三學生中進行調查，這些學生具有較高的數學水平，且來自全國各省市，所學的是新課改后的教材（剔除所學是課改前教材的被試），其三角函數的教與學情況有一定的代表性．正因為此，問卷調查的結果可與標準及高考命題的研究結果作比較．

問卷設計旨在了解大學數學專業(yè)學生三角函數知識的學習情況，分為兩個部分，第一部分一共4道題，是為了解學生在高中階段對標準中未涉及的三角函數相關知識點的學習情況．第二部分一共7道題，是為測試學生對三角函數知識點掌握的水平，其中第一道題是關于三角函數本質的理解，第二道題是三角函數定義的敘述，第三道題是三角函數圖象與性質的分析，第四道是關于輔助角公式的應用，第五至七道是關于三角公式的靈活運用，對三角公式靈活運用的題目從易到難，以大學對三角式化簡的要求來設置[7]．被試在獨立、閉卷的環(huán)境下完成測試卷，保證了測試結果的可信度．

3 研究結果與分析

3.1 標準中三角函數內容深度的研究結果與分析

如前所述，統(tǒng)計標準中“三角函數”部分知識點對應的深度賦值，見表3．結果顯示，標準對三角函數的定義、圖象與性質要求較高，在結果性目標上都達到了理解及以上水平；對三角恒等變換相關公式的要求達到了4，是結果性目標中最高水平；對三角公式的運用達到2，是中等水平；沒有提到反函數的性質、萬能公式；積化和差、和差化積公式沒有明顯體現(xiàn)，在簡單的三角恒等變換中以例子給出，對其要求較低．

表3 標準中“三角函數”知識點及其深度賦值

3.2 高考命題三角函數內容深度的研究結果與分析

根據SOLO理論，得到各省高考題三角函數各知識點在各水平的題量，綜合各省的統(tǒng)計結果，得到全國自主命題的16個省市高考題中三角函數各知識點各水平的總題量，計算百分比，統(tǒng)計結果見表4．

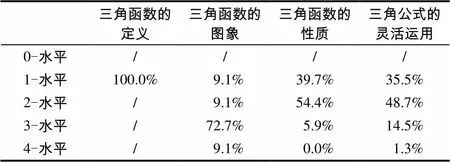
表4 全國自主命題的16個省市高考題關于三角函數各知識點深度所占比例

其中，對三角函數定義的考查處于1-水平，即特殊角的三角函數值，屬于純粹記憶，未考查到本質．對三角函數圖象的考查達到了4-水平，集中在3-水平，說明對三角函數圖象的考查較為深入，學生若能掌握由的伸縮變換過程，自然會，，的圖象以及推理能力和應用意識．對三角函數性質的考查達到了3-水平，集中在1-水平和2-水平，即三角函數性質的直接運用和性質的直接運用，已達到大學數學專業(yè)學習的要求．對三角公式的靈活運用達到了4-水平，但所占比例極少，主要集中在1-水平和2-水平，即三角公式的直接運用或多個三角公式同時運用，大學數學專業(yè)需要對三角公式靈活運用，此水平是不夠的．

3.3 大學數學專業(yè)學生三角函數知識深度的研究結果與分析

第一部分發(fā)放問卷283份，有效問卷269份．根據統(tǒng)計結果得各知識點各水平人數所占百分比，見表5．

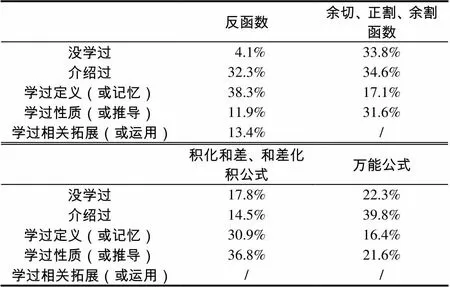
表5 大學生三角函數部分知識點學習的深度

根據表5，被試高中階段都接觸過反函數、余切函數、正余割函數、積化和差公式、和差化積公式、萬能公式，且各層次水平人數都不少，由于被試來自全國各省市，受教育的水平和環(huán)境不同，因此數據較為分散，說明雖然這些知識點在標準中已刪除，但中學教師仍會適當補充．

具體來說，對反函數，幾乎所有被試都了解，但極少數更深入地學習過反函數存在的條件及互為反函數的函數間的關系．互為反函數的函數間的關系能從本質上幫助學生理解反三角函數的圖象與性質，該知識的薄弱會影響大學反三角函數積分性質的學習．對余切、正割、余割函數，大學要求不高，只需知道其定義，尚有33.8%的被試沒有聽過．對積化和差公式、和差化積公式，67.7%的被試在高中階段學過且被要求記憶，32.3%的學生沒學過或不了解，還需改進．而萬能公式，在大學有著重要作用，但62.1%的被試對其完全沒學過或不熟悉．

第二部分發(fā)放問卷121份，有效問卷114份．按照SOLO理論對每個知識點不同水平的劃分，數據統(tǒng)計結果如表6所示．對三角函數定義的理解，只有22.8%的被試能理解三角函數既是數集到數集的對應，也是角到比值的對應，且是多對一函數，大多數被試還處于1-層次，只能理解其中一點．對三角函數的定義，雖中學要求掌握，但只有39.5%的被試能夠準確寫出定義，說明學生對三角函數定義的掌握是不好的．對三角函數的圖象與性質，52.6%的被試能想到3條以上，近半數對其不熟悉．對三角公式及輔助角公式的運用，大多數被試能化簡至較簡形式，但只有半數能得到最后結果，究其原因，可能是輔助角公式是教師額外補充的，標準中未作要求，所以被試掌握不夠，難以進行最后一步化簡．對三角公式的簡單運用、靈活運用和技巧性運用，大多數被試都能掌握兩角和差公式及拆角技巧，化簡至較簡形式，但極少數能得到最后結果，這3道題的最后一步都需要敏銳的觀察力、聯(lián)系的觀點方能找出式子特點，可見被試對三角公式運用的基本功不錯，但靈活運用的技能有待提高．

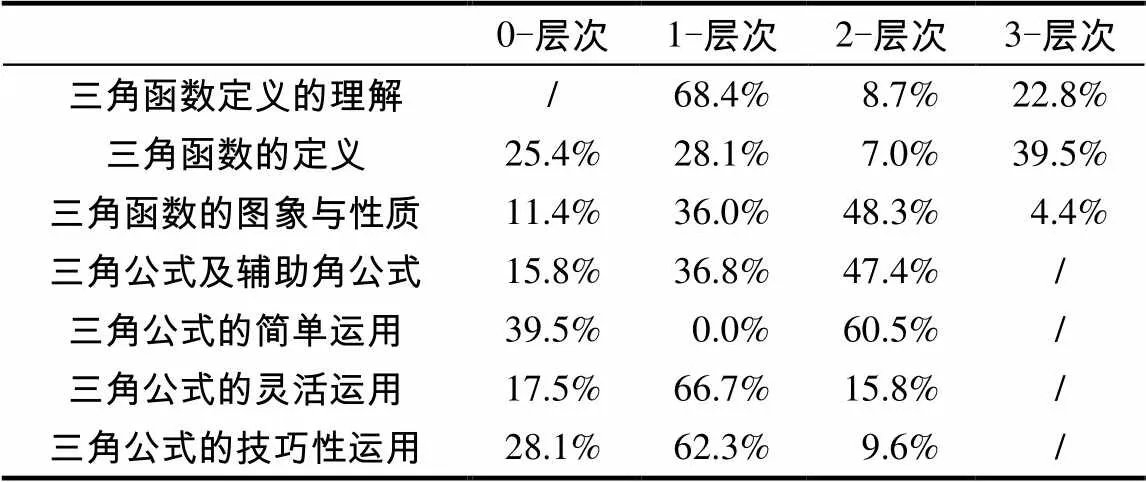
表6 大學生三角函數各知識點學習的深度

4 結論與建議

4.1 結 論

研究從3方面著手的結果是一致的，三角函數的定義雖然在標準中處于較高水平，但高考不考，所以學生對三角函數的本質掌握得不好，遺忘較快；三角函數的圖象與性質在標準中有較高要求，也是高考考查的重點，因此學生掌握得相對較好；三角公式的靈活運用在標準中處于中等水平，在高考也是公式的直接運用，因此學生能夠進行中等難度的三角變形，但不能進一步化簡．綜上，三角函數的定義雖未直接影響大學數學專業(yè)的學習，但其是三角函數圖象、性質的來源，間接影響著學生對三角函數的理解；三角函數的圖象與性質能較好地滿足數學專業(yè)的需求；三角公式的靈活運用水平還不夠，也影響了學生數學專業(yè)的學習．

對于標準未涉及的余切函數、正割、余割函數、積化和差、和差化積公式、萬能公式，高考幾乎未考，雖然許多教師都會額外補充這些知識，但從知識的系統(tǒng)性看，教師們并未從知識發(fā)生發(fā)展的角度去教，只是告訴學生結果，未研究其性質和運用．當然，這在有限的課時內是很難完成的．這也影響了數學專業(yè)的學習．

4.2 建 議

4.2.1 標準應適當調整三角函數部分內容

標準關于三角函數部分知識的刪除對學生后續(xù)大學學習造成了一定的影響．因此，對于反函數的概念、存在條件及互為反函數的函數間關系、積化和差、和差化積公式、萬能公式等內容，在標準的修訂、調整時應給予特別關注和研究，確定取舍．若增加，這些內容宜處于理解獨立操作及以上水平．如果學生能夠掌握反函數的存在條件及互為反函數的函數間關系，那么大學自學反三角函數的圖象與性質只需稍加點撥即可．

4.2.2 高考命題應增加考查三角函數定義的題型

高考命題直接影響著教師教學的內容和難易程度．由于高考不考三角函數定義，導致了學生對三角函數定義的學與練較少而掌握不牢．因此高考應適當增加考查三角函數定義的題目．如在考查解三角形、三角函數和向量相結合、角所在的象限等問題中將原本直接給出的條件如“”換成“角的終邊上有一點”．

4.2.3 高中教師應關注學生后續(xù)學習的需要并做好高中與大學的銜接

高中教師的教學需立足于學生長遠發(fā)展，了解高校高數教材，做好高中、大學的銜接．對于三角函數，教師可適當補充反函數的概念、存在條件及互為反函數的函數間關系、積化和差、和差化積公式、萬能公式等，講解時應遵循知識的發(fā)生發(fā)展過程，切忌對結果直接記憶．另外，還需加強三角化簡中常用變形技巧的訓練．

4.2.4 大學教師應主動了解中學所學并適當補充相關知識或組織學生自學

大學教師需主動研讀中學數學教材，關注學生的認知水平．對高中、大學內容脫節(jié)的地方，需適當補充或讓學生自學．對于三角函數，大學教師需補充或讓學生自學積化和差、和差化積公式、萬能公式，并加強對三角化簡的訓練．

4.2.5 大學生在學習的過程中發(fā)現(xiàn)有高中沒學到的知識應利用大學資源自學

高校都有機房、圖書館、選修課等資源，學生在學習過程中，發(fā)現(xiàn)高中、大學內容脫節(jié)的地方，應尋找途徑自學．對三角函數，學生需要自學反函數的概念、存在條件及互為反函數的函數間關系、和差化積公式、萬能公式，加強三角化簡能力．大學微積分計算大多涉及三角化簡，也可直接做微積分計算的題目來加強此項訓練，如《吉米多維奇習題集》就是不錯的選擇．

[1] 邱晨輝．中學教師向院士疾呼“救救數學”[N]．中國青年報（教育科學），2014-6版．

[2] 袁洲．大、中學數學教學銜接問題的研究綜述[J]．阜陽師范學院學報（自然科學版），2008，（1）：78-81．

[3] 柴俊，路競，俞曼．高考分數高，大學數學成績一定好嗎[J]．數學教學，2003，（8）：封面．

[4] 潘建輝．大學數學和標準課程下高中數學的脫節(jié)問題與銜接研究[J]．數學教育學報，2008，17（2）：67-69．

[5] 中華人民共和國教育部．普通高中數學課程標準（實驗）[M]．北京：人民教育出版社，2003．

[6] 劉艷．SOLO分類評價法及其應用研究[J]．宜春學院學報，2008，（S1）：158-160．

[7] 高等師范院校數學分析教學大綱[M]．北京：人民教育出版社，1980．

[8] 呂世虎，劉鵬飛．標準與大綱中函數內容難度的比較研究[J]．數學教育學報，2010，19（3）：63-66．

[責任編校：周學智]

Empirical Study on the Depth of Content of High School Trigonometric Function Based on University Mathematics Study

SHE Dan

(Nanjing Normal University, Jiangsu Nanjing 210097, China)

Based on university mathematics study, this paper studies the depth of Content of the high schooltrigonometric function from the curriculum standard, the proposition of college entrance examination and the level of College Students’ Mathematics. Quantitative and qualitative analysis have been both made more in details. The results shows that the depth of Trigonometric function’s definition and the flexible use of triangle formula did not meet the requirements of the university level, while product to sum and difference product formula, universal formulas for trigonometric transform, cotangent function which were deleted by the curriculum standard play an important role in the study of college mathematics majors.

curriculum standard; proposition of college entrance examination; level of college students’ mathematics; trigonometric function

G420

A

1004–9894（2016）06–0085–03

2016–08–10

教育部“南京師范大學卓越中學教師培養(yǎng)改革項目”

佘丹（1991—），女，湖北咸寧人，研究生，主要從事數學課堂教學、數學解題及數學評價研究．