漁業資源研究中II型錯誤與樣本容量關系的模擬研究

潘艷玉，王迎賓，徐元凱，邵裕真，錢亞婷

（浙江海洋大學水產學院，浙江舟山 316022）

漁業資源研究中II型錯誤與樣本容量關系的模擬研究

潘艷玉，王迎賓，徐元凱，邵裕真，錢亞婷

（浙江海洋大學水產學院，浙江舟山 316022）

在假設檢驗中經常會出現兩類錯誤，即“棄真”（I型錯誤）和“納偽”（II型錯誤）。通常研究者往往更加注重I型錯誤所帶來的危害，卻忽視II型錯誤的可能性，這一情況在漁業資源研究方面同樣存在。本文結合國內外對II型錯誤的研究現狀及我國漁業資源現狀，模擬產生10 000個魚類可捕體長數據作為總體，并從中隨機抽取不同的樣本容量，每個樣本容量重復抽取200次，分別計算各個樣本容量下的平均值、標準差、拒絕域以及各組犯II型錯誤的概率，并繪制概率密度分布圖，經過分析可得在其他條件相同的情況下，II型錯誤概率β隨著樣本容量的增加而呈現一定的下降趨勢。

假設檢驗；I型錯誤；II型錯誤；漁業資源；樣本容量

隨著漁業科學研究的不斷發展，數理統計學中的假設檢驗方法已在漁業領域得到廣泛應用，為推動水產業的發展起著非常重要的作用。假設檢驗作為數理統計學在漁業行業內最為常用的一種方法，是通過結合樣本信息，利用“小概率不可能性原理”對事先作出的假設進行檢驗，以接受或否定原假設，從而判斷樣品間的實質性差異是由樣品本身引起還是由不可控的因素干擾產生。

在進行假設檢驗時，所推斷的結論并非絕對正確，所以常需要考慮到兩類錯誤，即I型錯誤和II型錯誤，前者是指拒絕了實際上成立的原假設，即“棄真”，其概率用α表示；后者為接受實際上不成立的原假設，即“納偽”，其概率用β表示。

國外對II型錯誤方面的研究早在上個世紀30年代就已經開始了[1]，涉及水產研究領域中II型錯誤的問題研究到80年代才開始關注[2]。我國最早對假設檢驗中II型錯誤方面進行研究報道的是郭春彥[3]。1989年，郭春彥[4]發表了一篇關于對目前教育與心理統計書中I型錯誤及II型錯誤的分析，并以A地區高考語文平均成績為例，對I型錯誤與II型錯誤概率的反比關系進行探究，文中強調了在使I型錯誤的概率α盡可能小的同時，一定要注意II型錯誤的概率β的取值。在查閱文獻的同時，我們發現在各個領域顯著性檢驗的過程中，對II型錯誤的分析研究非常少見，由此可見，我國對II型錯誤還并不重視。

經王迎賓等[3]對國內6個水產類期刊2011-2015年這5年內發表的學術論文的查閱統計，在所查閱的3829篇學術論文中，進行顯著性檢驗的有2235篇，而分析了II型錯誤的文章為0篇。也就是在我國水產科學研究越來越深入的今天，大家的目光還是停留在犯I型錯誤概率上，而徹底忽視了犯II型錯誤可能會帶來的后果。然而，越來越多的研究實例表明，II型錯誤在漁業研究領域同樣具有著重要地位，對II型錯誤的研究能加強漁業研究的科學性，提高漁業管理的效率。

對于許多初次接觸假設檢驗的學者來說，往往會陷入一個誤區，就是認為犯I型錯誤的概率越小越好，也就是α的值越小越好。其實當其他條件都相同的時候，犯I型錯誤的概率α越小，拒絕域W的范圍越小，接受域范圍就相應的增大，則犯II型錯誤的概率β越大；相反，犯I型錯誤的概率α越大，拒絕域W的范圍越大，接受域范圍就相應的減小，則犯II型錯誤的概率β越小[5]。我們無法同時減小犯I型錯誤和II型錯誤的概率，也就是說犯這兩類錯誤的概率不是相互獨立，而是相互關聯的。

當α的值很小的時候，原假設H0一般不會被輕易拒絕。此時如果樣本落在拒絕域，那么作出的否定原假設的結論就相對比較可靠；相反的如果因為樣本落在接受域而選擇接受原假設的結論不一定可靠，因為這個時候犯II型錯誤的概率可能很大。在實際的應用中，應根據具體的情況，選取合適的α或者β，當人們不輕易拒絕H0的時候，α的值可以盡可能取小一點（最常用的是α=0.05和0.01，有時也用到0.001，0.10），β的值往往控制在0.10至0.30之間，因為在大多數假設檢驗中，第一類錯誤被認為更有害，更需要控制[6]。

可是在漁業資源研究中，有時II型錯誤可能帶來的危害會更大。2002年美國國家科研委員會一份報告顯示，漁業管理委員會在設定捕撈限額時對科學信息的忽略是引發過度捕撈的主要原因[7]。在某種程度上，科學信息是海洋漁業資源管理的關鍵[8]，而科學信息與假設檢驗又有著密不可分的聯系。例如，我們要研究在一定捕撈強度下某種漁業資源是否遭到破壞[3]，可以作出原假設H0：在該強度下漁業資源沒有顯著減小和備擇假設HA：在該強度下漁業資源會出現顯著減小。如果原假設為真而被我們拒絕了，根據這個檢驗結果，我們可能會適當地減小捕撈強度以保證漁業資源可持續發展，從而犯了I型錯誤，這一結果會影響漁民的收入水平，但是資源得到了保護，不會受到破壞。相反，如果原假設不正確，檢驗結果卻顯示在該強度下漁業資源沒有顯著減小，漁業工作者根據這一結論而繼續保持原有的捕撈強度，這將很有可能導致過度捕撈，資源受到破壞，由此可見，在漁業研究領域中II型錯誤可能會帶來更大的傷害，這應該引起漁業研究者的高度重視。本文通過模擬產生總體數據，并對隨機抽取不同樣本容量的樣本對II型錯誤概率β的影響展開研究。

1 材料與方法

本文所做的假設檢驗需要運用到的是z檢驗和t檢驗，這兩種檢驗方法的差異主要是由于總體方差的設定不同。通常當總體方差已知的時候，采用z檢驗，運用公式當總體方差未知的時候，采用t檢驗，這時需要運用到公式計算。這兩種檢驗統計量源出同根，只是在總體方差處理上有所不同，導致了檢驗方法的差異，實際上這兩種檢驗的絕對差異并不明顯[9]，均適用于本文的模擬研究。

由前文可知，II型錯誤概率β并非一成不變，而是和α有著密切關系，其他條件相同的情況下，α越大，β越小，反之，α越小，β越大。除此之外它還受到其他因素變化的影響，例如與真實值μ有關，用α來表示樣本檢測值μ0與真實值μ的差異，根據其相對距離（μ-μ0）/σ在其他條件相同時，其值越大則表明μ與μ0的差距越顯著，犯II型錯誤概率β越小[10]；此外，β值與樣本容量n也有著密不可分的關系。

本文以探究某種魚類種群是否面臨過度捕撈的危險為例，假設該魚類種群平均體長在150 mm及以上則表明屬于合理開發狀態即沒有面臨過度捕撈，若平均體長小于150 mm則已過度捕撈，需要重新控制捕撈強度以保護魚類資源可持續。

為了探究樣本容量n對β值的影響，我們利用電子表格軟件Excel進行統計分析，模擬某種魚類種群體長數據。假設該魚類資源可捕體長一般在100～200 mm，利用RAND函數隨機產生了10 000個體長數據，求得這個總體的平均體長為149.616 mm，總體標準差為28.78，在顯著性水平α=0.05條件下，拒絕域也就是說體長平均數大于149.527 mm，就應接受原假設。但是當原假設不正確的時候，將會導致II型錯誤發生。其概率求算為即II型錯誤發生的概率為62.19%，也就是我們此次模擬的真實值為62.19%。

利用INDEX函數從已經模擬出的10 000個數據中隨機取數，樣本容量分別為100、200、300、400、500、600、700、800、900、1000這10種情況，每種樣本容量各重復取樣200次，分別計算其樣本平均值、樣本標準差、拒絕域（分總體標準差已知和未知兩種）以及犯II型錯誤的概率β，根據已經求得的概率，運用NORMDIST函數求出其正態分布函數并結合概率畫出概率密度正態分布圖。

2 結果

當總體平均數和總體方差均已知時，采用z檢驗來處理數據，探究樣本容量與β的關系，通過在各樣本容量條件下拒絕域取值的變化對比觀察，不難發現，隨著樣本容量的增大，拒絕域xα的值也在不斷增大，但并不是像一次函數那樣無限增長，而是不斷趨近于總體的拒絕域約為149.53 mm（圖1）。

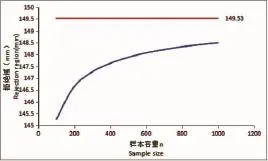
圖1 拒絕域與樣本容量的關系Fig.1 Relationship between rejection region and sample size

以每個樣本容量下每組的樣本標準差作為數據源，計算其波動離散程度即標準差，觀察表1，我們可以明顯的發現，當樣本容量較小的時候，各個樣本標準差的波動較大，不穩定。但是隨著樣本容量的增大，樣本標準差逐漸趨向穩定。

表1 樣本標準差與樣本容量的關系Tab.1 Relationship between sample standard deviation and sample size

根據II型錯誤概率β的概率密度分布圖（圖2）可知在其他情況都相同的時候，樣本容量不斷增加的同時犯II型錯誤的概率有一定的減小的趨勢，且不斷的靠近真實值62.19%。

圖2為在總體標準差已知，即總體標準差為28.78時所得到的II型錯誤概率密度分布圖，圖中直線為真實值62.19%，曲線部分由上至下分別是樣本容量為100、300、400、200、500、600、800、700、900、1000時的概率密度曲線，考慮到隨機取樣可能造成一定的誤差，所以我們得出，在控制其他條件相同的情況下，隨著樣本容量的增加，II型錯誤的概率有所減小。并且，對各個樣本容量下概率的峰值統計（表2），結合圖2，我們可以發現，隨著樣本容量的不斷增加，概率峰值有所下降，II型錯誤的概率不斷接近已知真實值。

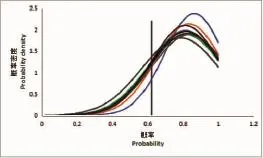
圖2 概率密度正態分布圖（已知總體標準差）Fig.2 Probability density distribution plot (totally standard deviation is known)

表2 概率峰值與樣本容量的關系Tab.2 Relationship between the probability of the peak and sample size

以上是模擬假設總體標準差已知的情況，但是在解決實際問題的時候，我們往往不知道總體標準差，這時就需要運用單樣本t檢驗進行檢驗，利用樣本標準差進行求算。通過對未知總體標準差時的拒絕域與已知情況時拒絕域的對比（表3），不難發現不管是已知還是未知總體標準差，拒絕域隨著樣本總量的增大而不斷接近總體拒絕域149.53 mm。當樣本容量較少時，拒絕域的波動范圍較大，隨著樣本容量的增大，拒絕域逐漸穩定趨近于總體拒絕域。

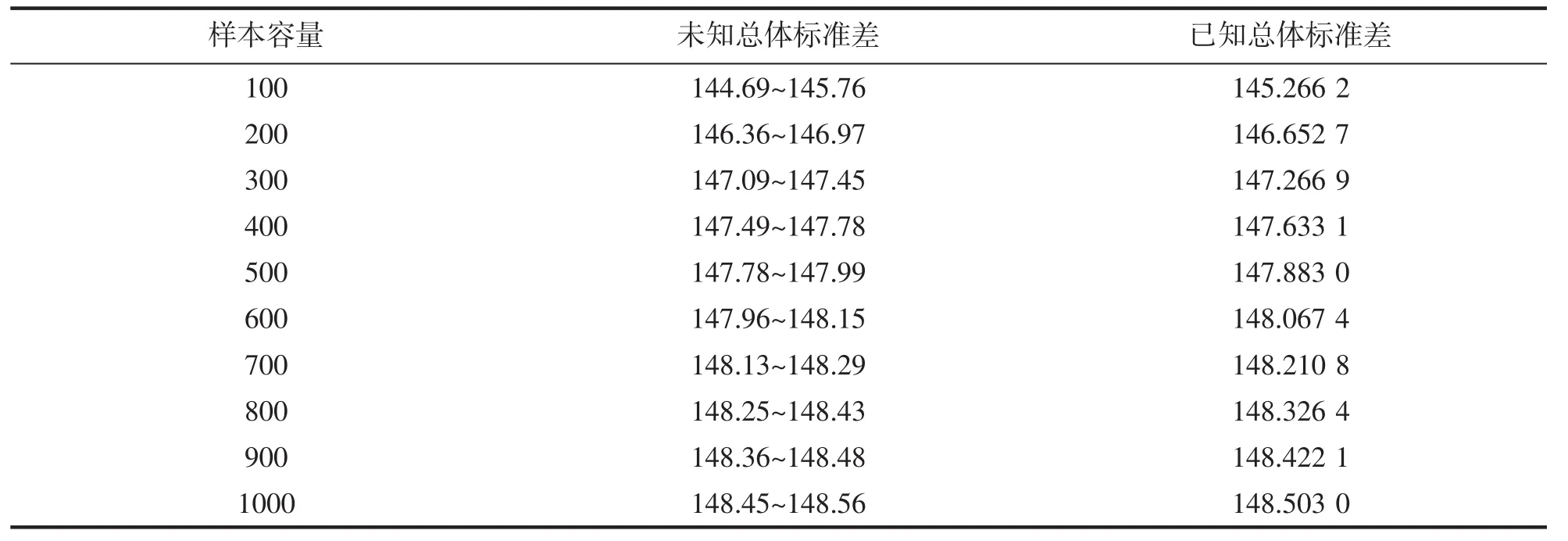
表3 兩種情況下拒絕域與樣本容量的關系Tab.3 Relationship between rejection region and sample size in two cases

圖3是在總體標準差未知時，利用樣本標準差求得的II型錯誤概率β的概率密度分布圖。根據其變化趨勢，不難發現利用樣本標準差進行計算出的概率β總體也是隨著樣本容量的增大呈現一個下降的趨勢且不斷接近真實值。

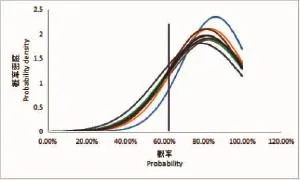
圖3 概率密度正態分布圖（未知總體標準差）Fig.3 Probability density distribution plot(when totally standard deviations unknown)

圖3中直線為真實值62.19%，曲線部分由上至下分別是樣本容量為 100、300、400、200、500、600、800、700、900、1000時的概率密度分布曲線。由于是用樣本標準差進行求算的，所以個別較用總體標準差的結果略有偏差，但是仔細觀察可以發現，它們之間的差距其實很小。其實相比總體標準差而言，利用樣本標準差更符合實際。

3 討論

如今，在多種研究領域中，大多都有涉及到顯著性檢測這一統計檢測方法。而據大量文獻資料查閱可知，在國外漁業資源領域中II型錯誤方面的研究最早是從上個世紀80年代開始的，而我國在這方面卻少有研究。特別在漁業資源評估中，假設檢驗占據重要地位，II型錯誤也應該引起廣大學者的關注。在實際應用中，根據實際情況需要，選取合適的樣本容量來控制II型錯誤發生的潛在危害將會有利于漁業生產和漁獲結構的改進，對提高我國漁業管理的科學性、盡快實現漁業資源的恢復具有積極意義。

本文通過模擬研究II型錯誤概率與樣本容量的關系，發現樣本容量的選擇在統計推斷中至關重要。當我們選取了合適的α來控制好I型錯誤的概率，其他條件一定時，樣本容量的選擇將會直接影響到II型錯誤的概率。由于實際中樣本容量通常自由選擇，因此往往無法做到控制概率β，也無法保證統計假設檢驗效果[11]。本文模擬工作得出犯II型錯誤的概率β隨著樣本容量的增大而有一定的減小趨勢這一結果，增加樣本容量n，是同時減小兩類錯誤的必要條件[12]，也就是說，在之后的假設檢驗的時候，我們可以適當的增大樣本容量使II型錯誤的概率控制在一定的范圍內。

然而樣本容量并非越大越好，在實際的漁業資源研究中，樣本容量的增大，勢必會造成實際操作成本的增加。例如我們想要了解一種魚類種群是否面臨過度捕撈危險，若想要控制一個很低的β而選擇一個很大樣本容量，則將需要捕撈大量該魚類種群，這必將增大漁業工作者的工作量，延長工作時間，且其操作成本也會有所提高。其最終的檢驗效果可能只是略高于一個較小的樣本容量，考慮到實際操作成本費用和實際情況，有時我們會選擇一個相對較合適的樣本容量進行檢驗，而不是越大越好。

4 結語

本文存在的不足是沒有繼續探究如何去選取一個具有實際操作性和適應性的樣本容量。在假設檢驗應用越來越廣泛的今天，II型錯誤也應逐漸被重視起來，本文通過模擬研究淺談了II型錯誤與樣本容量的關系，我們大致得出在其他條件都相同的情況下，犯II型錯誤的概率β隨著樣本容量的增大而有一定的減小趨勢，同時隨著樣本容量的增大概率β不斷接近真實值。在漁業資源研究領域中，若這一結論被更多的工作者，管理者關注的話，相信將更加有助于準確揭示捕撈作用對群落結構和生態系統的影響機制。

[1]TANGP C.The power function of the analysis of variance tests with tables and applications of their use[J].Statistical Research Memoirs,1938,2(2):126-149.

[2]PETERMAN R M,ROUTLEDGE R D.Experimental management of Oregon coho salmon(Oncorhynchus kisutch):designing for yield of information[J].Canadian Journal of Fisheries and Aquatic Sciences,1983,40(5):1 212-1 223.

[3]王迎賓,俞存根,陳 勇.水產科學研究中被忽視的II型錯誤[J].水產學報,2016,40(1):135-143.

[4]郭春彥.對目前教育與心理統計書中I型及II型錯誤的分析[J].北京師范學院學報:自然科學版,1989,10(2):57-64.

[5]蘇再興,王志福,管 杰,等.假設檢驗中兩類錯誤及其關系的探討[J].科技信息,2010(35):117-233.

[6]孫成霖.淺談假設檢驗中的兩類錯誤及樣本含量的關系[J].價值工程,2010,29(6):39.

[7]韓 勇.美國漁業資源的管理和保護[J].海洋開發與管理,2006,23(3):91-92.

[8]諸曉琳.預警原則在中國海洋漁業資源管理中的適用[J].海洋通報,2010,29(3):289-294.

[9]智冬曉,許曉娟,張皓博.z檢驗與t檢驗方法的比較[J].統計與決策,2014(20):31-34.

[10]甘倫知.假設檢驗中控制第二類錯誤的探討[J].統計與決策,2011(22):35-37.

[11]勵晶晶,郭 文.兩類錯誤條件下的樣本容量選擇[J].統計與決策,2010(15):14-18.

[12]蘇新富.假設檢驗的錯誤分析[J].遼寧師專學報,2012,14(2):7-8.

Simulation Studies of the Relationship between Type II Error and Sample Size in the Researches of Fishery Resources

PAN Yan-yu,WANG Ying-bin,XU Yuan-kai,etal
(Fishery School of Zhejiang Ocean University,Zhoushan 316022,China)

Two types of mistakes often appear in hypothesis testing,namely the"reject a true null hypothesis"(type I error),and"accept a false null hypothesis"(type II error).In a general inspection,researchers usually pay more attention to the damage which caused by type I error,and ignore the possibility of type II errors. This situation also exists in the fishery resources research.Based on the domestic and foreign researches of type II errors and the present situation of fishery resources in China,we simulated 10 000 data,and then from which we randomly drew different samples with different sample sizes.For each sample size,we repeated the simulation process 200 times.Sample means,standard deviations,rejection region and the probability of type II errors of different sample sizes were calculated,and the figures of probability density distributions were drawn. The results showed that when other conditions were the same,the probability of type II error β showed de－creasing trend with the increase of sample size.

Hypothesis test;type I error;type II error;fishery resources;sample size

S91

A

1008－830X(2016)05－0425－05

2016-07-10

國家自然科學基金（31270527）；浙江省公益性技術應用研究計劃項目（2015C33094）；浙江省自然科學基金（LY13D010005）；浙江省本科院校中青年學科帶頭人學術攀登項目（Pd2013222）；2015年浙江海洋學院大學生科技創新項目（xj201508）

潘艷玉（1994-），女，浙江青田人，研究方向：海洋資源與環境.E-mail:18368095282@163.com

王迎賓（1979-），博士，教授，研究方向：漁業資源與種群動力學.E-mail:yingbinwang@126.com