瓦斯在煤體中的非線性滲透模型及求解

呂 伏，徐曾和，梁 冰，孫維吉

(1.東北大學資源與土木工程學院，遼寧 沈陽 100083；2.遼寧工程技術大學基礎教學部，遼寧 葫蘆島 125105；3.遼寧工程技術大學研究生學院，遼寧 阜新 123000)

瓦斯在煤體中的非線性滲透模型及求解

呂 伏1,2，徐曾和1，梁 冰3，孫維吉3

(1.東北大學資源與土木工程學院，遼寧 沈陽 100083；2.遼寧工程技術大學基礎教學部，遼寧 葫蘆島 125105；3.遼寧工程技術大學研究生學院，遼寧 阜新 123000)

考慮到外力引起的孔隙結構改變，將導致煤體滲透性發生顯著變化，利用原煤試件的三軸滲透實驗數據建立反應瓦斯非線性滲流規律的數學模型，采用基于改進遺傳算法賦初值的擬牛頓法求解建立的模型，對瓦斯在原煤試件中的非線性滲流規律進行了求解和分析。結果表明，改進的遺傳算法大幅提高了初值尋找的速度和精度，為利用擬牛頓法進行模型最終求解提供保障，從而使得新型優化算法可以有效解決非線性最小二乘問題。采用該方法研究煤體的非線性滲流規律發現，在一定壓力范圍內，煤體的滲透系數隨孔隙壓力增加而增加，隨體積應力的增加而減小，滲透系數是孔隙壓力的二次函數與體積應力的負指數函數的乘積。

煤；滲透系數；遺傳算法；非線性最小二乘；參數反演

1 研究背景

多孔介質廣泛存在于自然界、工程材料和動植物體內。滲流力學是研究流體與多孔介質的共同作用以及流體在多孔介質中運動規律的科學[1]。1856年，法國工程師Darcy總結出了線性滲流定律(Darcy定律)，自此滲流力學迅速成為了解決地下水、石油、天然氣開發等工程中關鍵技術問題的有力工具。伴隨近年來煤炭行業的發展[2-3]，石油工業的崛起，材料科學及生物醫學的發展，滲流力學更得到了廣泛的關注和應用。

國外很多學者已經注意到了多孔介質變形對滲流的影響，并通過理論及試驗研究，探討了裂隙巖體、非飽和土等多孔介質中的非線性滲透規律，并結合試驗給出了較為實用的滲透系數模式[4-8]。Heiland等[9]、schulze等[10]、Oda等[11]進行了全應力-應變過程中巖石滲透性變化的試驗，觀察了巖石的滲透性在其變形直到破壞整個過程中的變化。國內學者龔鋼延等[12]、張伯崇等[13]通過試驗研究了試驗研究了破碎巖石在不同孔隙結構下的滲流特性巖石滲透率與圍壓和孔壓的關系。Xiexing Miao等[14]試驗研究了破碎巖石在不同孔隙結構下的滲流特性。

瓦斯在煤體中的運移規律，關系到煤礦的瓦斯涌出量預測，突出危險性及瓦斯抽放難易程度評價，直接影響煤與瓦斯共采過程中瓦斯抽采方式的選擇[15]，進而影響著礦井瓦斯的抽放設計。能否合理地給出煤體的滲透系數，研究清楚瓦斯在煤體中的滲流運動是關系煤礦的安全開采及瓦斯的合理開發利用的關鍵因素。

一定條件下，煤體是可變形的。在煤體發生形變的時候，包含在其中的孔隙也會隨之發生改變，這樣就會引起在孔隙空間中賦存并運移的氣體流量也發生變化。與此同時，孔隙空間中的氣體壓力又會參與孔隙結構的改變和煤體的變形。因此，煤體中氣體的運移是煤體變形同氣體運動共同作用的結果。同時，煤對瓦斯又具有吸附特性，瓦斯的吸附解吸作用，以及在低壓條件下瓦斯的滑脫效應等均對瓦斯的運移產生影響。宏觀上，這種影響表現為滲流過程中煤體的滲透系數是關于孔隙壓力及體積應力的函數而不是常數，也即煤體的非線性滲流規律[16]。

Somerton W.H.等[17]研究了三軸應力作用下氮氣及甲烷氣體在裂紋煤體中的滲透性，指出，隨地應力增加，煤層透氣率按指數關系減小。周世寧、林伯泉等[18]研究了受載作用下瓦斯在煤樣中的滲透特性，得出煤樣的滲透率與應力間關系如下：加載過程中服從指數函數關系k=ae-bω；卸載過程中服從冪函數關系：k=k0σ-c。孫培德等[19]研究了應力和孔隙壓力與煤層的瓦斯滲透率之間的關系，并得到以下結論：①孔隙壓力一定，煤層的滲透率隨有效應力的增加而減小，隨有效應力的減小而增加，二者呈負指數的變化規律；②當煤體骨架所承受的有效體積應力處于穩定狀態時，滲透率隨孔隙壓力呈對數坐標下的拋物線型變化規律。以上研究，定性地給出了滲透系數函數模型，為多場耦合作用下瓦斯運移規律的研究提供了堅實的基礎。

然而在確定非線性滲透系數中的未知參數時，作為因變量的滲透系數，作為自變量之一的氣體孔隙壓力值(有效應力是孔隙壓力和體積應力共同作用的結果)都是煤體的三軸滲透實驗無法直接測得的，這樣利用實驗數據，采用直接法進行非線性滲透系數的反分析會遇到困難。為了采用直接法求解，通常做法是利用瓦斯的三軸滲透實驗測得的氣體流量值，根據線性Darcy定律計算出滲透率，再通過回歸分析來實現待定系數的求解。這樣在實驗操作上簡便易行，計算上簡單，但存在以下兩個方面的問題：①既然考慮滲透系數的非線性，即是認為進行的滲透實驗本身是非線性的，對于非線性的滲透實驗，代用線性的滲透定律求解出的滲透率本身就存在問題，再將計算完的結果拿來作為回歸分析數據求解所設的非線性滲透系數中的未知參數，顯然有悖于研究初衷；②實驗過程中只能控制試件兩端的孔隙壓力，這樣在穩定滲流階段認為壓力梯度均勻是合理的，但即使是在此前提下，試件中的孔隙壓力值也應該是變化的，采用什么位置的孔隙壓力值進行回歸計算，是不可回避的問題。有鑒于此，構造合適的采用間接方法反求煤體非線性滲透系數的最小二乘數學模型，及模型的有效求解方法非常必要。

借鑒文獻[20]求解人工制備的多孔介質的非線性滲透系數的方法，在研究氣體在原煤試件中的非線性滲流規律過程中，進行了原煤試件的三軸滲透實驗，實驗過程中試件一端的氣體流量數據可測，試件的軸壓和圍壓可控，試件兩端的孔隙壓力可控，在此基礎上依據煤體試件中氣體運移的質量守恒方程，構建出關于試件一端流量的最小二乘模型。由于該模型的高度非線性，采用高斯牛頓等方法求解時初值獲得較為困難，采用遺傳算法等方法求解時收斂速度慢，都難以快速精確的得到理想結果。基于此，提出一種基于改進遺傳算法提供初值的擬牛頓法，綜合利用搜索法和迭代法，從而有效求解所建立的模型，快速、準確地得到原煤試件的非線性滲透系數。

2 原煤試件的三軸滲透實驗

2.1 實驗設計

為研究煤體的滲透系數與總應力和孔隙壓力間的關系，先后使用巖石切割機和2DM-200型自動(手動)磨石機將從現場采集的煤樣加工成標準試件，實驗室對加工的原煤試件進行三軸甲烷氣體滲流實驗。

本實驗使用的儀器包括：改進過的 ZYS-1 型真三軸滲透儀，手動試壓泵，數字壓力表，六通閥，儲能器，氣源氣瓶，高壓調壓閥，量筒，水槽，DDS 數據采集系統，計算機，高壓管線等。

實驗系統主要由煤樣加載壓力室，軸壓、圍壓加載系統，氣體孔隙壓力加載系統，穩壓系統，煤樣變形量采集系統及氣體流量測量系統組成。煤樣軸壓及圍壓由手動試壓泵供給，加壓后通過蓄能器保持壓力穩定；孔隙壓力由高壓甲烷通過氣體壓力調節閥調節達到所要求的數值；孔隙壓力、圍壓及軸壓數值是利用高精度的數字壓力表測定的；滲流氣體量值由排水法通過量筒直接讀取。在控制圍壓為2MPa和3MPa情況下在0～1.5MPa范圍內分別改變5種軸壓共計進行了10組測試，每組測試又在0～2.5MPa范圍內分別改變5種孔隙壓力，最終得到共計50組實驗數據。

圖1 實驗數據分析圖

2.2 數學模型的構建

通過實測的流量和實驗控制的軸壓、圍壓及孔隙壓力信息，明顯看到氣體在煤體中的流量隨體積應力及孔隙壓力的變化而變化。顯然，無論隨體積應力還是孔隙壓力的變化都不是簡單的線性變化規律。通過對實驗數據的整理分析發現，如圖1所示，在控制孔隙壓力不變的情況下，流量隨體積應力的變化呈非線性遞減變化的趨勢，而在控制軸壓和圍壓不變的情況下，流量隨孔隙壓力的變化呈現非線性遞增變化的趨勢。因而假設煤體的滲透系數見式(1)。

k(p,σ)=(ap2+bp+c)e-dσ

(1)

氣體在原煤試件中的流動為一維軸向流動，穩定滲流階段符合如式(2)所示的運移規律。

(2)

式中：p 為孔隙壓力，單位MPa，σ為介質應力，單位MPa，本文計算中采用的是體積應變，對于一維壓縮而言，體積應變即其軸向應變；a,b,c為度量孔隙壓力變化對滲透系數改變的影響的常數；d 為度量體積應力變化對滲透系數改變的影響的常數。

容易求得從一端流出試件的流量的理論值，見式(3)、式(4)。

(3)

(4)

在三軸滲流試驗中，試件兩端的孔隙壓力p、介質應力(軸向應變)σ是試驗的可控條件，即為已知量。將p、σ代入式(1)，可求解出從一端流出試件的流量的理論值Q。同時，試驗中還容易得到穩定滲流階段由試件一端流出的實際流量Q’。采用最小二乘的思想，選取理論流量與實測流量差的平方和為目標函數，見式(5)。

f(x1,x2,x3,x4)=

(5)

式中：(x1,x2,x3,x4)=(a,b,c,d)；s為試件的截面積，cm2；l為試件長度，cm；n為試驗的次數。

則參數反演問題轉化為求使得目標函數f最小的(x1,x2,x3,x4)=(a,b,c,d)的非線性最小二乘問題。

3 模型的求解方法

3.1 求解方法的基本思想

當滲透系數成為非線性函數的時候，反分析問題構造出的是非線性最小二乘問題(式(4))，求解非線性最小二乘問題最經典的方法就是高斯-牛頓法。該方法的基本思想是，基于導數，定出初始搜索方向，然后從初始條件出發逐步迭代尋找最優解。近年來，圍繞收斂速度問題演變出了多種改進的高斯-牛頓法，為了避免求導數帶來的大量運算，還有學者提出了不依賴導數的擬牛頓法[21]。但無論增加阻尼因子還是不依賴導數，始終解決不了該類方法嚴重的初值依賴問題。而本文所建立的非線性最小二乘模型，其初值的獲得又非常困難，因此求解該問題關鍵在于如何尋求合適的初值。

遺傳算法，是一種啟發式隨機搜索算法，利用轉移概率規則來幫助指導搜索，通過編碼，復制，交換，變異等操作來模擬生物物種的自適應進化過程，實現對目標函數的優化。本文選擇遺傳算法進行初值尋找的主要原因是考慮了其如下兩方面的優勢[22]：①遺傳算法回避導數運算，以目標函數值為直接搜索信息，降低了算法的運算量和難度；②遺傳算法屬于多點并行搜索，搜索速度快，范圍大，從而減少了結果陷入局部極小值的可能。

本文在前人研究基礎上，利用遺傳算法的優勢來計算初值，在此基礎上最終利用不依賴導數的擬牛頓法求解非線性最小二乘模型。將搜索法和迭代法相互結合，各取其長。但是運算速度和計算量成為了制約該方法的關鍵因素，初值尋找的速度和精度直接影響該算法能否進行。有鑒于此，本文采用了一種改進的遺傳算法，在傳統遺傳算法的基礎上進行合理優化，大幅度提高初值計算的速度和精度，從而使得該算法可以順利解決所建立的數學模型。算法總體流程如圖2所示。

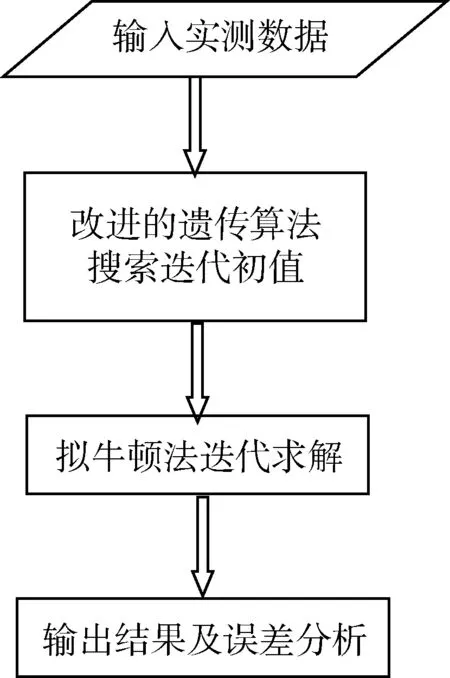
圖2 算法總體流程圖

3.2 遺傳算法的改進

由于遺傳算法搜索空間巨大，在減少陷入局部極小值的同時不可避免的有運算速度慢的問題，從而導致參數反演過程計算量過大。具體表現在以下三方面。

首先在初始群體規模的選擇上，理論上講規模越大，越容易得到精度好的結果，但是初始群體規模增大勢必會導致下面的遺傳操作中巨大的運算代價，而初始群體規模太小，又會使迭代次數增加，也會減慢搜索速度；其次，在復制階段，若完全按照自然界的自適應法則進行進化，其速度往往很慢，反應在運算上，即是迭代次數多，運算量巨大，并且很容易不收斂，陷入死循環；最后，在交換環節，因同代中往往存在相同個體，若單純隨機選擇個體交換，無法保證交換的有效性。

本文采用了改進的遺傳法，在傳統的遺傳算法基礎上做了如下幾方面的改進。

1)在初始種群的選取上借鑒海選方法，采取普遍發展，擇優錄用的策略。即先大規模隨機生成種群，然后在種群中選取最優的部分進行后面的遺傳操作。

2)在復制階段加入判斷準則，仿照“優生”，只允許好的個體進行復制，加快了進化速度。

3)在交換之前進行判斷，保證不同的個體之間進行真正有效的交換。

具體算法如下所示。

1)編碼。根據問題的實際意義，選取個體長度用來儲存二進制編碼。

2)生成初始種群。采用隨機生成的方法產生大規模初始種群。

3)確定適應度函數。按數值大為適應度好的規定，取最小二乘目標函數的倒數為適應度函數。并計算初始種群中各個個體的適應度。

4)優選個體。選取適應度最好的部分個體進行下面的遺傳操作。

5)優生復制。計算個體的復制概率，然后按照概率復制，同時保證復制的個體優于上一代對應位置的個體。

6)交換。選擇不同的兩個個體，隨機進行單點交換。

7)變異。按一定的概率，隨機選擇基因進行變異(1變成0，變成1)。

重復算法5)～7)過程，直至得到滿意的結果[23]。

3.3 改進的遺傳算法驗證算例

為檢驗改進的遺傳算法相對于傳統遺傳算法的優越性，采用文獻[24]中一組人工制備的多孔介質材料的實驗室三軸滲流試驗實測數據做為算例進行檢驗。設滲透率為如式(6)所示的指數模型。

k(n)=k0eap-bσ

(6)

式中：k0為初始孔隙率；p為孔隙壓力，MPa，σ為介質應力，MPa，本文計算中采用的是體積應變，對于一維壓縮而言，體積應變即其軸向應變；a為度量孔隙壓力變化對孔隙率改變的影響的常數；b為度量總應力變化對孔隙率改變的影響的常數；s為試件的截面積，cm2；l為試件長度，cm；n為試驗的次數。

采用最小二乘的思想，選取理論流量與實測流量差的平方和為目標函數，見式(7)。

(7)

式中：(x1,x2,x3)=(k0,a,b)；s為試件的截面積，cm2；l為試件長度，cm；n為試驗的次數。

則參數反演問題轉化為求使得目標函數f最小的(x1,x2,x3)=(k0,a,b)的非線性最小二乘問題。

如表1所示，其中的計算流量1為用改進的遺傳算法經過100次迭代，得到的結果。此時對應的參數值為：k0=0.3555,a=16.5090,b=0.1732，共計用時5.5733s，平均相對誤差為3.7429%。計算流量2為用傳統的遺傳算法經過800次迭代，得到的平均相對誤差為3.83%結果。此時共計用時55.72秒。可見改進的遺傳算法在運算時間和精度上都有大幅度的提高，可以為擬牛頓法提供有效的初值。為新算法的進行提供了有力保障。

4 瓦斯在原煤試件中運移規律分析

上文描述在實驗室中進行了原煤試件中甲烷氣的三軸滲透實驗，根據這50組實測數據，采用上述的基于改進遺傳算法賦初值的擬牛頓法對氣體在原煤試件中的非線性滲透系數進行反演，均取得了較好的結果，篇幅所限，表2、表3列出其中二組實測數據進行計算的結果。

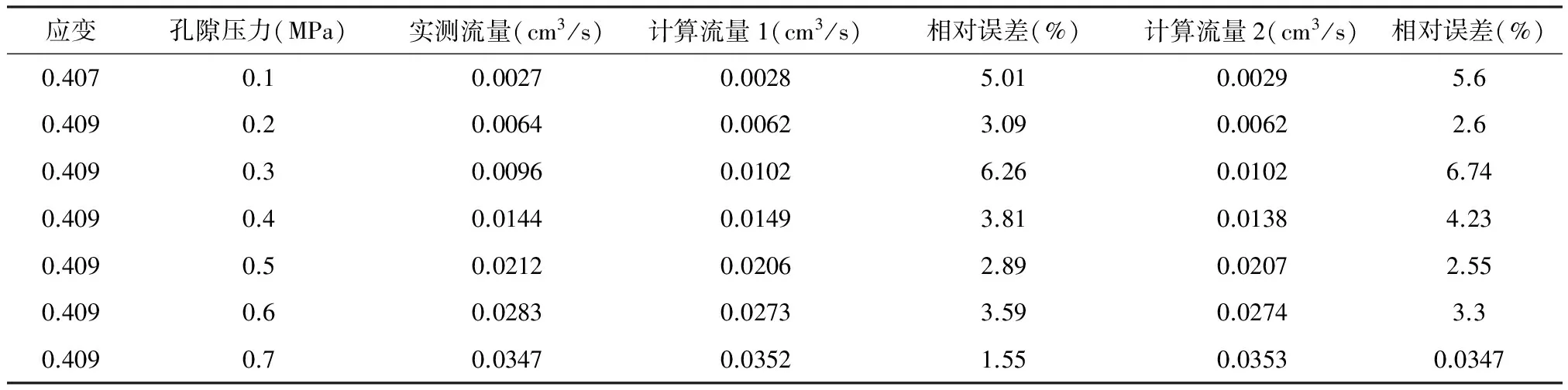
表1 驗算結果對比表

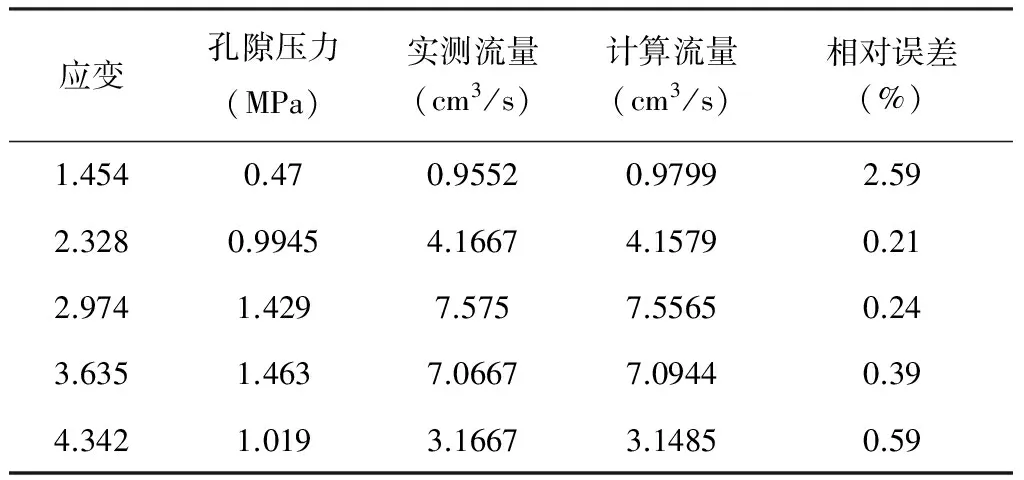
表2 計算結果1

注：此時的非線性滲透系數為：K=(-11.1803p2+62.2611p-3.5330)e-0.1621σ。

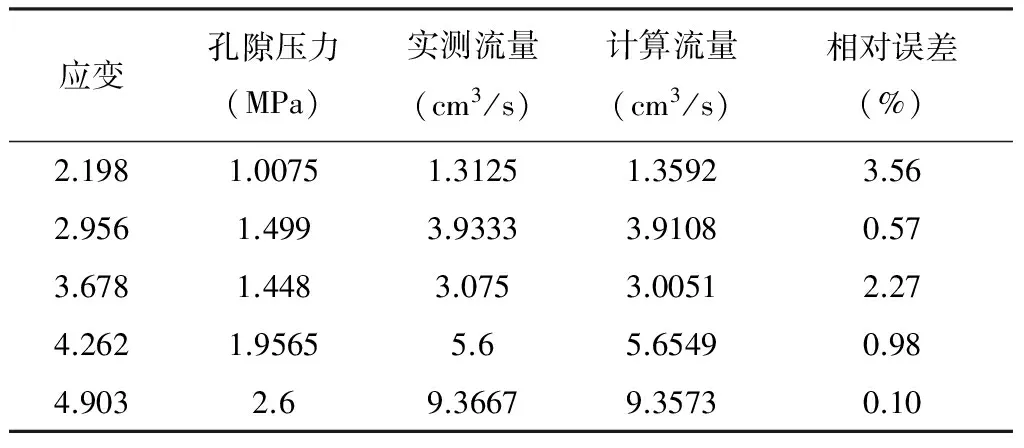
表3 計算結果2

注：此時的非線性滲透系數K=(-3.2061p2+52.2622p-16.4455)e-0.2346σ。

由表2、表3中計算結果可見，采用文中所設非線性模型描述原煤試件的滲透系數，可以較為精確的計算出試件一端的氣體流量。按照求解出的滲透系數，我們可以看到，在控制體積應力不變的情況下，滲透系數隨孔隙壓力呈二次函數關系遞增，即孔隙壓力越大，滲流量越大。這是由于孔隙壓力的增大，導致煤體試件中的孔隙裂隙擴張，同時試件兩端的壓力梯度也隨之加大，從而導致氣體流量增大。在控制孔隙壓力不變的情況下，滲透系數隨體積應力呈負指數關系變化，即隨著體積應力越大，流量越小。這是由于體積應力的增大，導致煤體試件中的孔隙裂隙壓縮，即氣體的流通通道變小，從而導致試件一端實測的氣體流量變小。在文中所研究的實驗設置條件下，圍壓控制在2MPa和3MPa,軸壓控制在0.5M～1.5MPa,孔隙壓力控制在0.5M～2.5MPa范圍時，煤體試件處于彈性變形階段，得到的滲流規律與前人的相關研究結論是基本一致的。

5 結論及展望

1)采用改進的遺傳算法，在保證同樣精度情況下，用時大概只有傳統的遺傳算法十分之一，可見，該方法在多參數、非線性最小二乘問題的求解過程中可大幅提高計算速度。

2)借助原煤試件的三軸滲透試驗及一維穩定滲流的數學模型構造了反演滲透性參數的非線性最小二乘問題，并采用基于改進的遺傳算法賦初值的擬牛頓法求解了該問題，結果具有較高的精度。

3)本文為煤體非線性滲透系數反演提供了一種簡便可行的方法，對于文中的試件，基于二次函數與指數函數乘積形式的滲流模式得到了滿意的結果，對于其他情況，可以根據其實測數據改變滲流模式做類似的運算來反演其滲透系數。

4)通過文中計算，瓦斯在煤體中的滲流具有明顯的非線性特性，滲透系數隨體積應力及孔隙壓力的變化而呈現非線性變化規律，不再滿足Darcy定律，文中給出了描述該非線性滲流規律的具體模型描述和有效的求解方法，為礦井瓦斯的抽放設計及流固耦合模型理論研究煤與瓦斯共采提供了必要的前提。

[1] 趙陽升.多孔介質多場耦合作用及其工程響應[M].北京：科學出版社，2010.

[2] 魏建平,秦恒潔,王登科，等.含瓦斯煤滲透率動態演化模型[J].煤炭學報，2015,40(7):1555-1661.

[3] 袁梅,許江,李波波，等.氣體壓力加卸載過程中無煙煤變形及滲透特性的試驗研究[J].巖石力學與工程學報，2014,10.33(10):2138-2147.

[4] Olivella S,Gens A.Vapour transport in low permeability unsaturated soil with capillary effects[J]. Transport in porous media，2000，40(3)：219-241.

[5] Rutqvist Jonny,Stephansson Ove.The role of hydromechanical coupling in fractured rock engineering[J].Hydrogeology Journal,2003,11(2):7-40.

[6] Birkholzer Jens,Li Guomin,Tsan Chin_Fu,Tsang Yvonne.Modeling studies and analysis of seepage into drifts at Yucca Mountain[J].Contaminant Hydrology，1999,38(5):349-384.

[7] Jones F.O.A.Laboratory study of the effects of confining Pressure on fracture flow and storage capacity in carbonate rocks[J].Petrol.Technol,1975(1):21-27.

[8] J.B.Walsh.Effect of pore pressure and confining pressure on fracture permeabilit[J].Int.J.Rock.Min.Sci.& Geomech. Abstr,1981,18:429-435

[9] Heilan J,Raab S.Experimental investigation of the influence stresspermeability of a lower Permian (Rotliegend)sandstone deformed in the brittle deformation field[J].Physics and Chemistry of the Earth,Part A:Solid Earth and Geodesy,2001,26(1-2):33-38.

[10] Schulze O,Popp T.,Kern H,T.Damage growth and permeability in deforming rock salt[J].Engineering Geology,2001,61(2-3):163-180.

[11] Oda,M.,Takemura,T.,Aoki,T.Damage growth and permeability change in triaxial compression tests of Inada granite[J].Mechanics of Materials,2002,34(6):313-331.

[12] 龔鋼延，謝原定.巖石滲透率變化的試驗究[J].巖石力學與工程學報,1989,8(3):219-227.

[13] 張伯崇,M.圍壓和孔隙壓力作用下花崗巖的滲透性狀[J].地球物理學報,1989(32):260-268.

[14] Xiexing Miao . Shuncai Li . Zhanqing Chen . Weiqun Liu. Experimental study of seepage properties of brokenSandstone under different porosities[J].Transport in Porous Media, 2011, 86:805-814

[15] 呂伏,梁冰,王巖等.基于因子分析的開采層瓦斯抽采方式選擇[J].中國安全生產科學技術,2014,10(7):26-31.

[16] 徐曾和.滲流的流固耦合問題及應用[D].沈陽：東北大學,1998.

[17] Somerton W.H.etal.Effect of stress on permeability of coal[J].International Journal of Rock Mechanichal Mining Science,1975,12(5-6):129-145.

[18] 林柏泉,周世寧.煤樣瓦斯滲透率的實驗研究[J].中國礦業學院學報,1987,16(1):2l-28

[19] 孫培德.變形過程中煤樣滲透率變化規律的實驗研究[J].巖石力學與工程學報.,2001,20(zk):1801-1804.

[20] 徐曾和,徐小荷,徐繼軍.可變形多孔介質滲透系數的測定方法.[J]. 實驗力學,1998,13(3):314-320

[21] 黃象鼎，曾鐘剛，馬亞南.非線性數值分析的理論與方法.[M].武漢:武漢大學出版社,2004:79-117

[22] 魏培君,章梓茂,韓華.雙相介質參數反演的遺傳算法[J].固體力學學報,2002,23(4)：459-462.

[23] 陳剛,郭嗣琮.信息科學中的軟計算方法[M].沈陽:東北大學出版社,2001:257-378.

[24] 宮麗麗.顆粒型多孔介質非線性滲流特性的試驗研究[D]. 沈陽：東北大學,2009.

Non-linear seepage model and it’s solusion methods of gas in coal body

LYU Fu1,2, XU Zenghe1, LIANG Bing3,SUN Weiji3

(1. College of Resources and Civil Engineering, Northeastern University, Shenyang 110819, China；2. Department of Basic Teaching,Liaoning Technical University,Huludao 125105,China; 3. Graduate School, Liaoning Technical University,Fuxin 123000,China )

Considering the changes of pore structure caused by the external force led to significant changes to the permeability of coal.Using the three shaft seepage test, gets the flow of the raw coal specimen through controlled the axial compression and confining pressure constant,solved the nonlinear least squares problem by using the quasi-newton method which gets the initial value by the improved genetic algorithm,then analysis and solves the non-linear seepage laws of the coal. The results show that the the new optimization algorithm can effectively solve the nonlinear least squares problem due to it solves the serious path dependence of the quasi-newton method and needn’t derivation during calculation process,it provides a feasible method to solve the non-linear seepage laws of the coal. Study on nonlinear seepage law of coal body by the method，we found that the permeability coefficient of coal increases with the increase of pore pressure and decreases with the increase of the volume stress,it’s the product of a quadratic function of the pore pressure and the negative exponential function of the volume stress.

coal; permeability parameter; genetic algorithm; nonlinear least squares; parameter inversion

2016-09-20

國家自然科學基金項目資助(編號:50974030)；博士后科學基金項目資助(編號:20110491512)

呂伏(1980-)，女，遼寧臺安人，東北大學工程力學博士研究生，任職于遼寧工程技術大學基礎教學部數學教研室，副教授 ，主要從事滲流力學中的數值計算方法及反演算法方面的工作,E-mail： lvfu123@sohu.com。

TP028.8

A

1004-4051(2017)01-0166-06