可控彎接頭鉆井工具的偏心機構控制仿真實驗

張光偉 劉暢

西安石油大學機械工程學院

隨著旋轉導向鉆井技術的不斷發展，對非常規油氣田的開采漸漸成為焦點［1］。國外對旋轉導向鉆井技術的研究比國內要早，技術上也比國內成熟。目前旋轉導向鉆井技術［2-3］主要分為：靜態偏置推靠式、動態偏置推靠式［4］、靜態偏置指向式和動態偏置指向式［5］，但動態指向式旋轉導向鉆井工具一直未被攻克。西安石油大學研制了一種可控彎接頭旋轉導向鉆井工具［6-7］，該鉆井工具屬于動態指向式旋轉導向鉆井工具。

1 偏心環控制方法

Control method for eccentric ring

西安石油大學研制了一種可控彎接頭旋轉導向鉆井工具，示意圖見圖1。

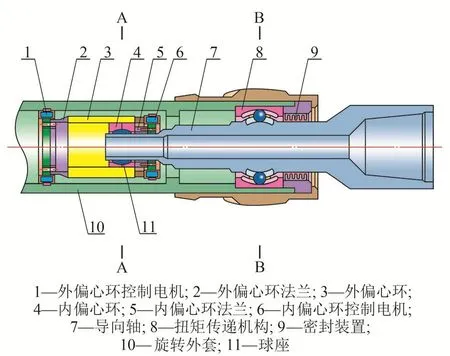
圖1 可控彎接頭鉆井工具結構示意圖Fig. 1 Schematic structure of drilling tool with variable angle bent sub

圖2為調整偏心環偏置狀態分析圖。

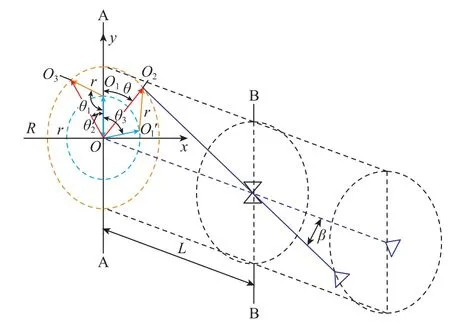
圖2 調整偏心環偏置狀態分析圖Fig. 2 Analytical diagram of offset state adjustment of eccentric ring

圖2中，點O2為某一導向軸偏置目標位置，導向軸方位角目標位置為θ，方位角θ是造斜工具裝置角，導向軸偏置角β在A-A截面即偏心機構截面偏擺距離為R，偏置角β的大小會影響工具鉆井井斜角的大小［8-9］，A-A 截面到 B-B 截面距離為L［10］。向量OO1'是從外偏心環偏心孔芯軸線到內偏心環偏心孔芯軸線，向量O1'O2是從外偏心環芯軸線到內偏心環偏心孔芯軸線即導向軸芯軸線，外偏心環芯軸線到內偏心環芯軸線距離與內偏心環芯軸線到導向軸芯軸線距離相等且均為r。偏心機構調整過程為，外偏心環不動，內偏心環先調整，如圖調整到與點O2同心等半徑圓的點O3位置，保證了導向軸偏置角β在A-A截面即偏心機構截面偏擺距離為R。內偏心環順時針轉動，轉過角度為θ1，此時向量OO3與向量OO1夾角為θ2，向量OO3與向量O3O1夾角為θ2。此時已經實現了導向軸偏置角β的調整。然后調整外偏心環，為了保證最終向量OO2與OO1'夾角為θ，即實現導向軸方位角目標位置為θ，讓外偏心環順時針轉動，轉過角度為θ3。此時本次偏心機構調整完畢。

通過對圖2的分析，可得調整導向軸偏置角β的公式為

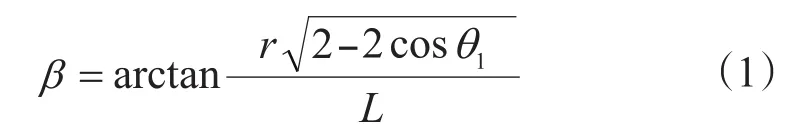
因為

所以只要

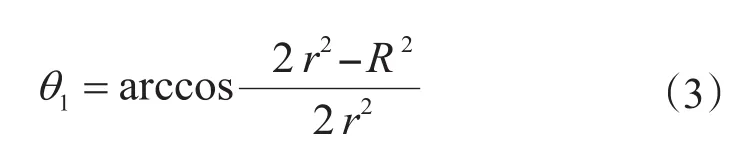
成立，式（1）即成立。

調整導向軸方位角θ的公式為

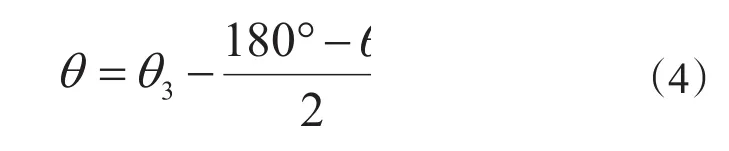
2 仿真建模

Modeling

2.1 機械建模

Mechanical modeling

如圖3所示，通過SolidWorks軟件，建立偏心機構三維模型。圖3中，黑色圓環為旋轉外套，綠色為外偏心環，藍色部分為軸承，紅色部分為內偏心環，白色部分為導向軸，黑白花斑圓盤為外偏心環電機等效盤。

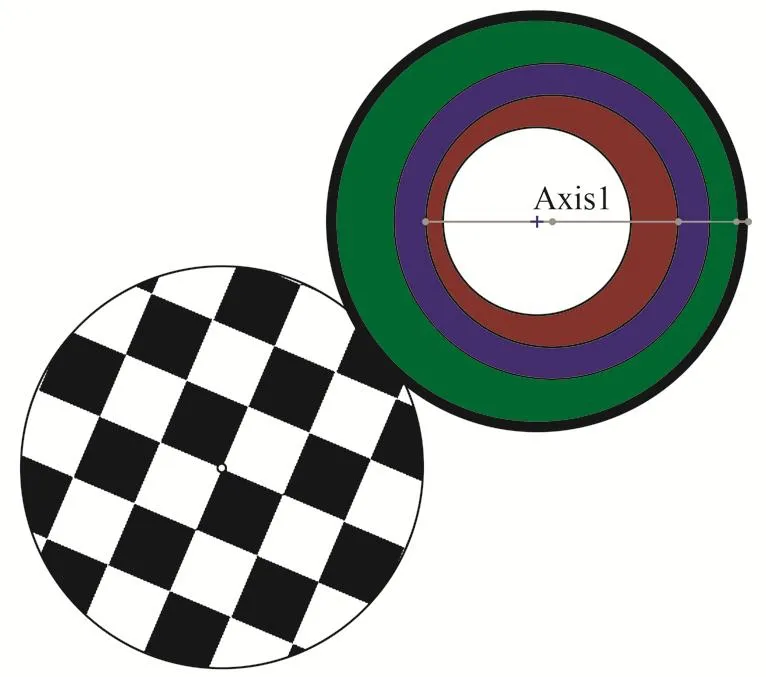
圖3 SolidWorks三維模型Fig. 3 SolidWorks 3D model

2.2 電氣建模

Electric modeling

通過SolidWorks軟件中的Motion插件，對已經建立好的三維模型進行電氣建模。如圖4，給紅色的內偏心環、綠色的外偏心環和黑色的旋轉外套添加電機選項，使得內偏心環、外偏心環和旋轉外套可以轉動。

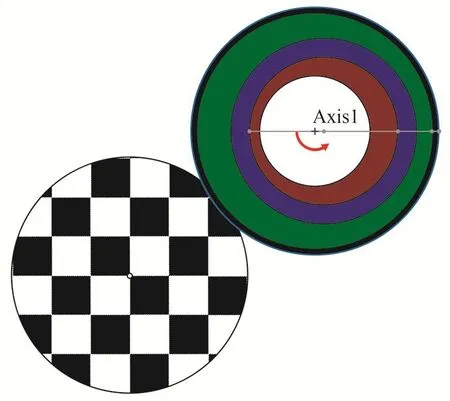
圖4 Motion電氣建模Fig. 4 Motion electric modeling

2.3 控制建模

Control modeling

在Labview軟件［1］的“程序框圖面板”中建立電機的控制程序，如圖5。電機控制程序編寫完成，Labview軟件的“前面板”中顯示控制電機運動的各類參數，如圖6所示，實現電機的界面化控制，方便快捷，互動性強。

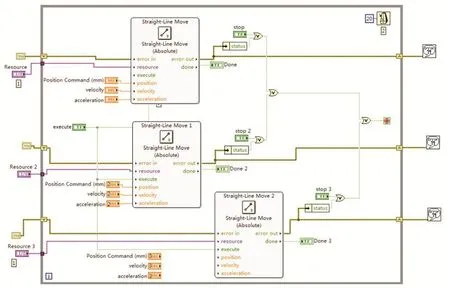
圖5 Labview控制程序Fig. 5 Labview control procedure

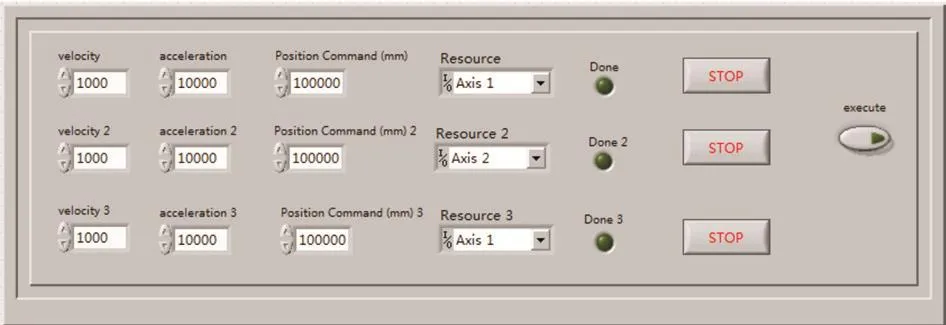
圖6 電機控制參數Fig. 6 Electromechanical control parameter

2.4 聯合仿真

Joint simulation

通過NI SoftMotion插件，可實現Labview與SolidWorks之間的聯合操作，即可通過Labview中建立好的電機控制程序去控制SolidWorks中的三維模型和電機，三者之間的關系如圖7。

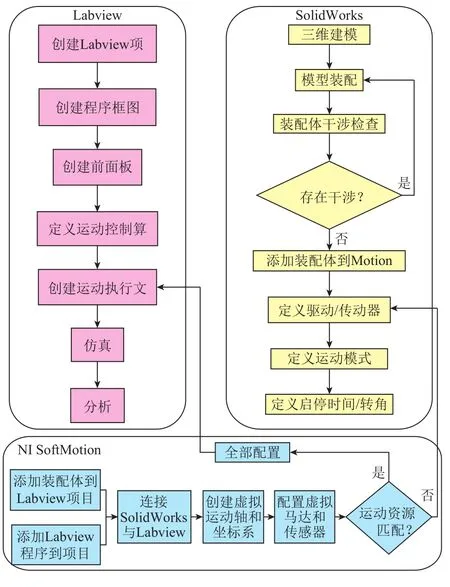
圖7 Labview軟件、SolidWorks軟件和NI SoftMotion之間的關系圖Fig. 7 Relationships between Labview, SolidWorks and NI SoftMotion

3 仿真結果

Simulation result

3.1 只調節內偏心環

Adjustment of internal eccentric ring only

根據控制方法，工具每次調整都先調整內偏心環從而調整偏心機構偏置角度β。為驗證控制方法中調整偏心機構偏置角度的正確性，設置內偏心環電機初始值然后依次調節內偏心環轉過角度為0°、60°、120°、180°。通過仿真實驗得到表 1 中的數據。

表1 只調節內偏心環偏時內偏心環轉過角度與擺距離R的關系Table 1 Relationship between the rotation angle of internal eccentric ring and the pivot distance (R) while only the internal eccentric ring is adjusted

用牛頓插值法［1］將表1中的數據做出一個牛頓插值多項式

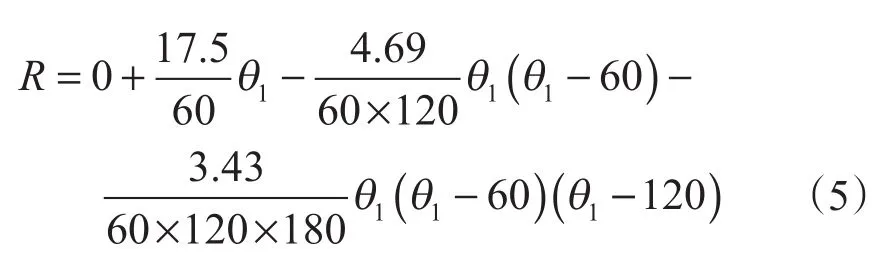
用 MATLAB［1］輸出式（5）的曲線，如圖 8所示。

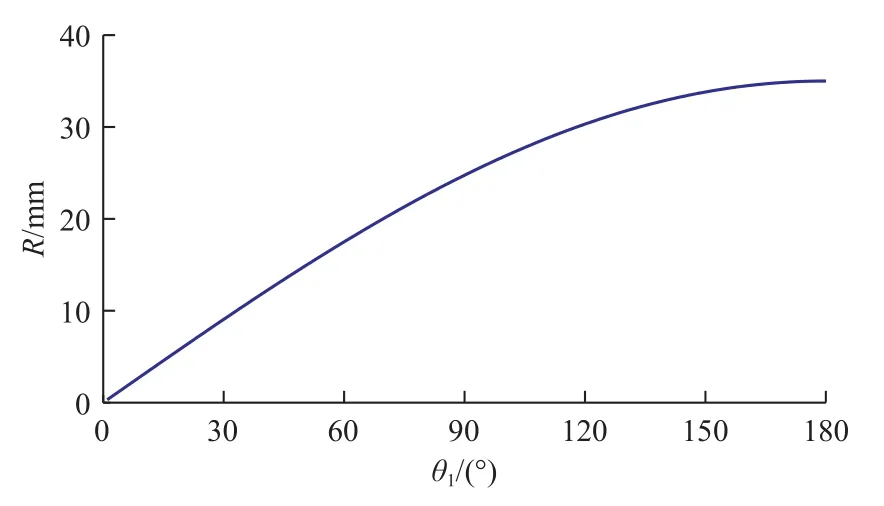
圖8 R與θ1仿真數據曲線Fig. 8 R and θ1 simulation data curves

將式（5）輸出曲線與式（3）曲線做對比，如圖9所示。兩曲線重合。偏置角度β在偏心機構周向截面偏擺距離為R，且為一一對應關系。只要式（3）中偏擺距離R與θ1關系正確，那么偏置角β與θ1的關系也就正確。將表1中的仿真結果代入式（3）中，驗證式（3）是正確的，即偏置角度β式（1）是正確的。

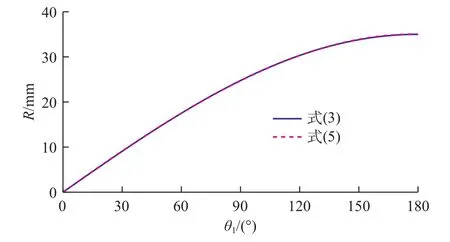
圖9 R與θ1仿真數據曲線與調整導向軸偏置角β公式曲線對比圖Fig. 9 Correlation of R and θ1 simulation data curves vs. offset angle (β) adjustment formula of guide shaft

再次進行驗證：隨機選取仿真結果代入偏置角β式（1），進行驗證，式（1）均能滿足，證明式（1）正確。

導向軸在A-A截面運動軌跡如圖10所示。

3.2 只調節外偏心環

Adjustment of external eccentric ring only

（1）當θ1=0°時（特殊情況），通過仿真實驗得到表2中的數據。

選取表2中的4組數據，用牛頓插值法將選取的數據做出一個牛頓插值多項式

與式（4）在θ1=0°時的簡化式不一致。因為在θ1=0°時，圖1中的OO1O3已不再構成是三角形，三角形的內角和公式不再適用。此時為特殊情況，當θ1=0°時，圖1中OO1與OO1'重合，實際工具處于最小偏置狀態，即零偏置狀態。在偏心機構調整的初始狀態下，調整偏置角度β=0，導向軸的方位角θ僅與外偏心環順時針轉過角度θ3有關，且與外偏心環順時針轉過角度θ3保持一致。故當θ1=0°時，θ=θ3。

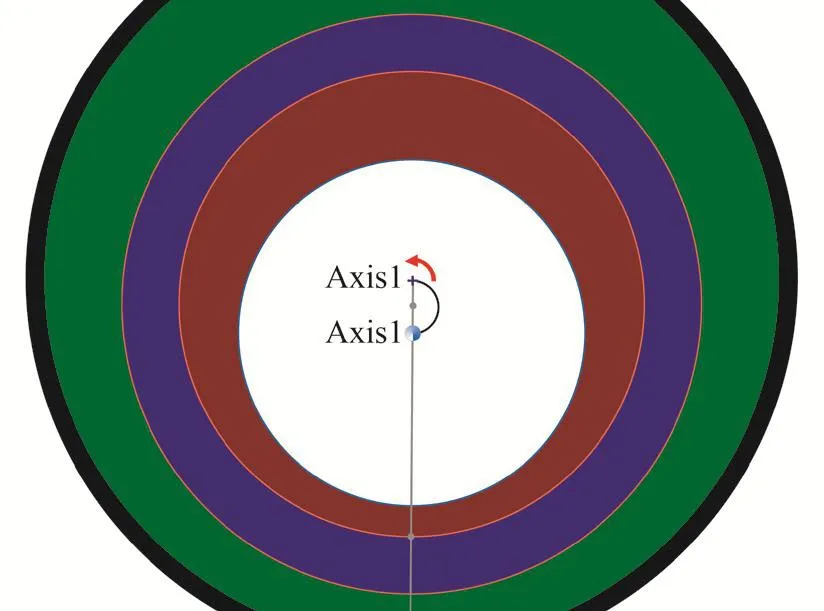
圖10 調整導向軸偏置角β時導向軸運動軌跡Fig. 10 Moving path of guide shaft when its offset angle (β) is adjusted

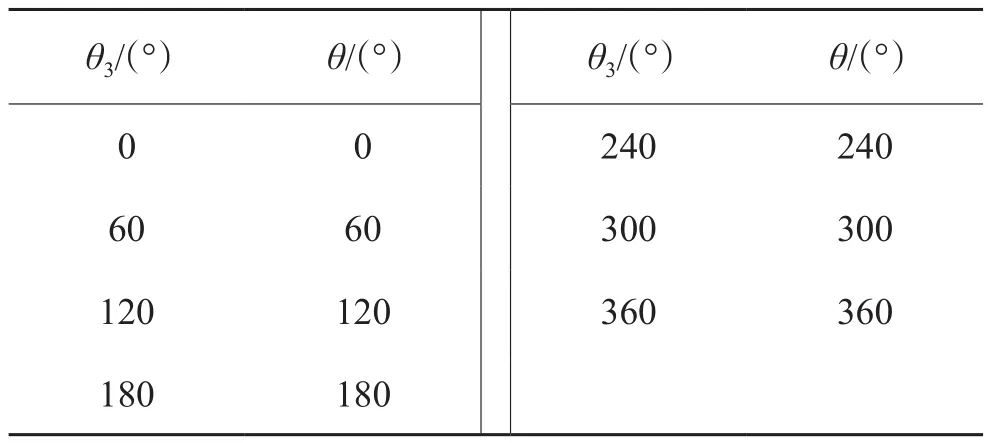
表2 當內偏心環轉動角度為0°時外偏心環轉過角度與方位角關系Table 2 Relationship between rotation angle and azimuth angle of external eccentric ring while the rotation angle of internal eccentric ring is 0°

當內偏心環不動即θ1=0°，外偏心環旋轉1周，導向軸也運動1周，但由于內偏心環不動，導向軸在A-A截面的運動軌跡僅為一個點。如圖11所示。

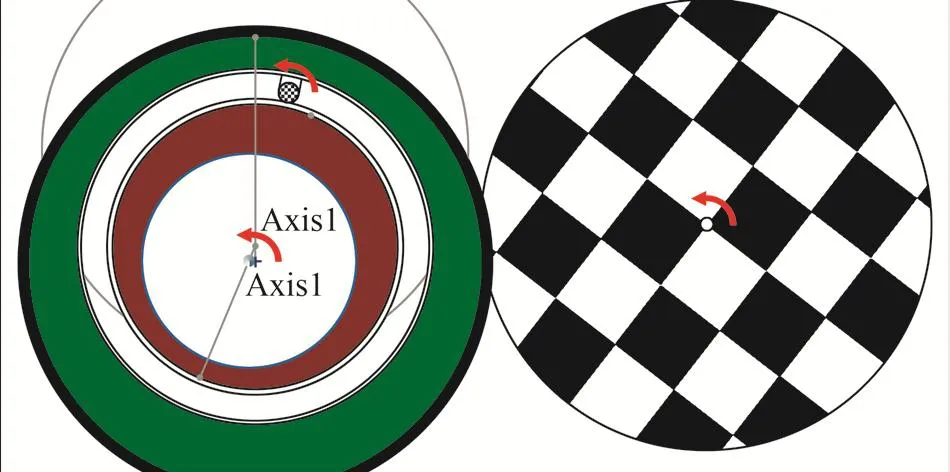
圖11 θ1=0°時，調整導向軸方位角θ導向軸運動軌跡Fig. 11 Moving path of guide shaft while its azimuth angle θ is adjusted in the case of θ1=0°

（2）當θ1=60°時，通過仿真實驗得到表3中的數據。

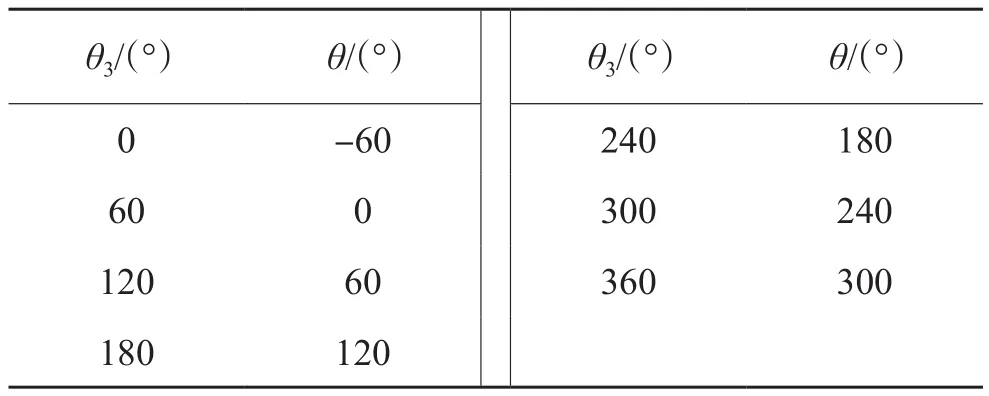
表3 當內偏心環轉動角度為60°時外偏心環轉過角度與方位角關系Table 3 Relationship between rotation angle and azimuth angle of external eccentric ring while the rotation angle of internal eccentric ring is 60°

選取表3中的4組數據，用牛頓插值法將選取的數據做出一個牛頓插值多項式

式（7）與式（4）在θ1=60°時的簡化公式完全一致。此時導向軸在A-A截面運動軌跡如圖12所示。

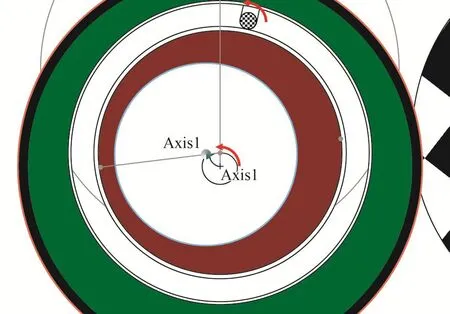
圖12 θ1=60°時，調整導向軸方位角θ導向軸運動軌跡Fig. 12 Moving path of guide shaft while its azimuth angle θ is adjusted in the case of θ1=60°

（3）當θ1=120°時，通過仿真實驗得到表4中的數據。

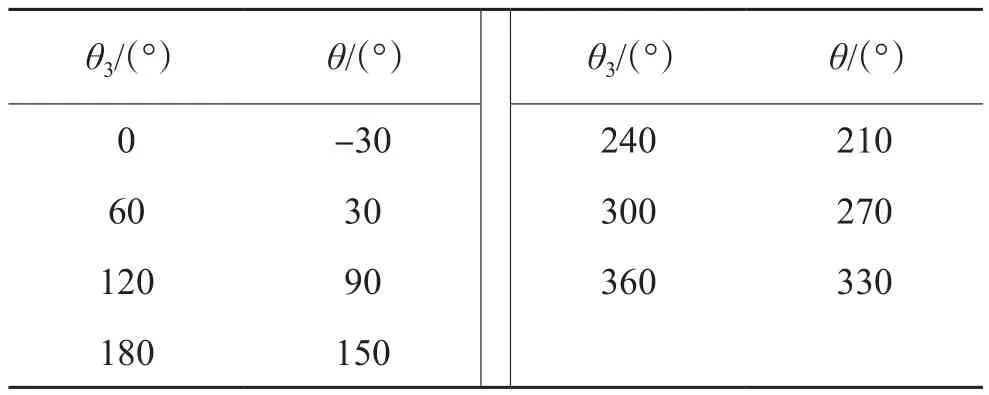
表4 當內偏心環轉動角度為120°時外偏心環轉過角度與方位角關系Table 4 Relationship between rotation angle and azimuth angle of external eccentric ring while the rotation angle of internal eccentric ring is 120°

選取表4中的4組數據，用牛頓插值法將選取的數據做出一個牛頓插值多項式

式（8）與式（4）在θ1=120°時的簡化公式完全一致。此時導向軸在A-A截面運動軌跡如圖13所示。

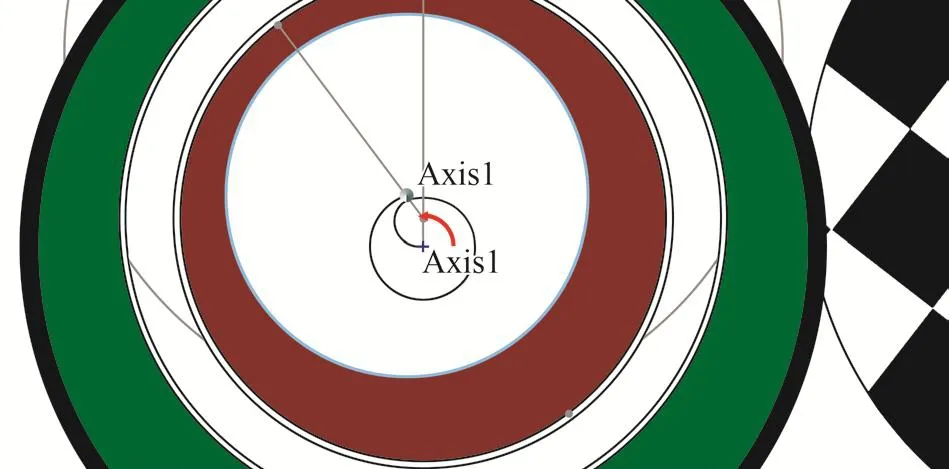
圖13 θ1=120°時，調整導向軸方位角θ導向軸運動軌跡Fig. 13 Moving path of guide shaft while its azimuth angle θ is adjusted in the case of θ1=120°

（4）當θ1=180°時，通過仿真實驗得到表5中的數據。

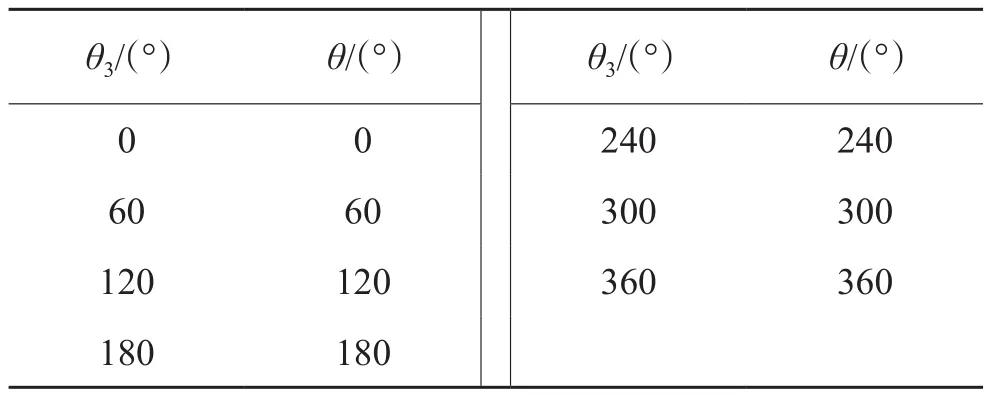
表5 當內偏心環轉動角度為180°時外偏心環轉過角度與方位角關系Table 5 Relationship between rotation angle and azimuth angle of external eccentric ring while the rotation angle of internal eccentric ring is 180°

選取表5中的4組數據，用牛頓插值法將選取的數據做出一個牛頓插值多項式

式（9）與式（4）在θ1=180°時的簡化公式完全一致。此時導向軸在A-A截面運動軌跡如圖14所示。

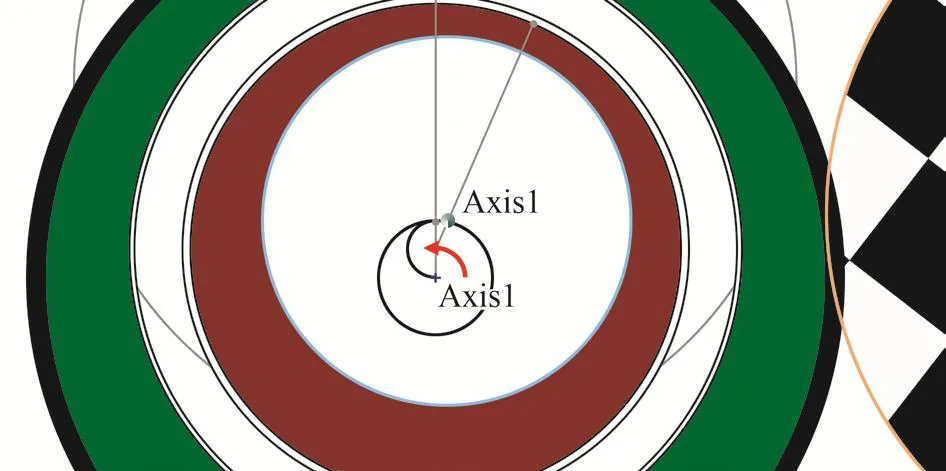
圖14 θ1=180°時，調整導向軸方位角θ導向軸運動軌跡Fig. 14 Moving path of guide shaft while its azimuth angle θ is adjusted in the case of θ1=180°

再次進行驗證：隨機選取上表中仿真結果代入導向軸方位角θ式（4）中進行驗證，式（4）均能滿足，證明式（4）正確。

3.3 外套不旋轉同時調節內外偏心環

Adjustment of internal and external eccentric rings without rotating the sleeve

通過前兩節分析當外套不旋轉時，內偏心環從0°調整到180°，偏心機構偏置角度β從0°變化到最大，即在A-A截面偏心機構截面偏擺距離R從0變化到最大；外偏心環從0°調整到360°，偏心機構導向軸的方位角θ也完整地旋轉360°。

外套不旋轉的情況下進行仿真，內偏心環從0°調整到180°，外偏心環從0°調整到360°，偏心機構截面偏擺距離R從0變化到最大，得到的數據如圖15所示，與式（3）和式（4）聯合做出的圖一致。

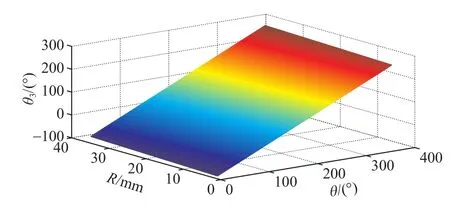
圖15 R、θ與θ3的三維關系圖Fig. 15 3D relationship between R, θ and θ3

證明外套不轉的情況下，同時調節內外偏心環，式（1）和式（4）也適用。

隨機選取一組數據：內偏心環順時針旋轉角度為60°，外偏心環順時針旋轉角度為360°時，導向軸在A-A截面運動軌跡如圖16所示。

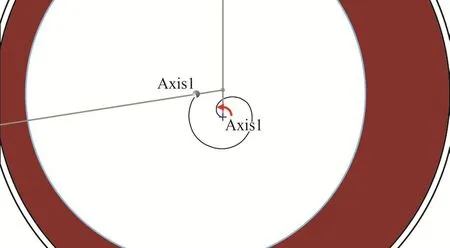
圖16 外套不轉情況下同時調節內外偏心環導向軸運動軌跡Fig. 16 Moving path of guide shaft while internal and external eccentric rings are adjusted without rotating the sleeve

3.4 外套旋轉同時調節內外偏心環

Adjustment of internal and external eccentric rings with sleeve rotation

基于該工具的特殊結構，外套旋轉時，外偏心環電機與之反向旋轉使得外偏心環相對于大地靜止，內偏心環電機不轉，使得內偏心環相對于外偏心環靜止，即相對于大地靜止。當外套旋轉時，外偏心環轉過的角度，實際為外偏心環電機轉子與外套之間通過轉速差實現的。

3.4.1 外偏心環初始位置誤差 開始仿真時，發現在理想情況下，整個工具從靜止狀態到旋轉穩定狀態，外偏心環電機轉子與外套之間沒有相對產生轉速差，即外偏心環相對于大地的位置沒有變化，外偏心環啟動的初始位置誤差為0（圖17）。

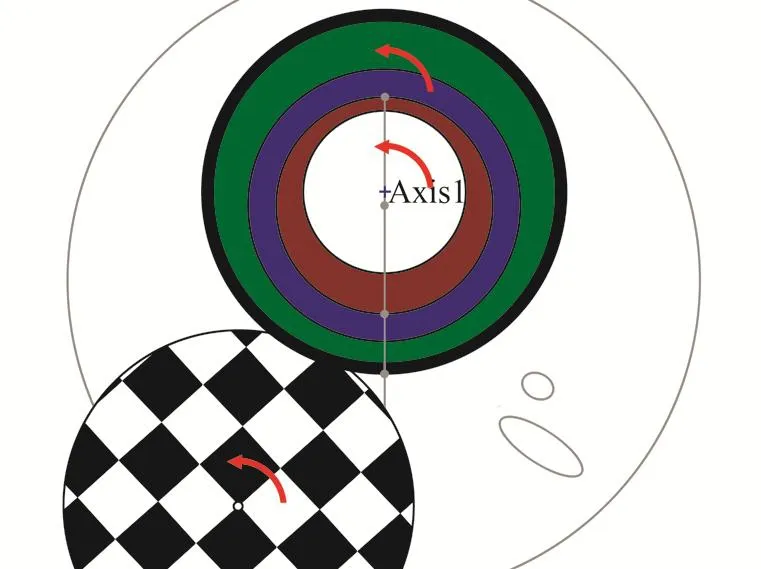
圖17 外套和外偏心環均旋轉時的初始狀態Fig. 17 Initial state while both sleeve and external eccentric ring are rotated

經過仿真研究發現，外偏心環電機加速度與外套加速度相同時，外偏心環啟動的初始位置誤差為0；外偏心環電機加速度與外套加速度不同時，外偏心環啟動的初始位置會有誤差。

3.4.2 調節內偏心環轉動對工具導向的影響 通過仿真實驗，測試數據與表1只調節外偏心環測試數據一致，證明式（1）在外套旋轉的情況下也適用。

3.4.3 調節外偏心環轉動對工具導向的影響 內偏心環電機無轉動時即當θ1=0°時，只調節外偏心環，通過仿真實驗得到表6中的數據。

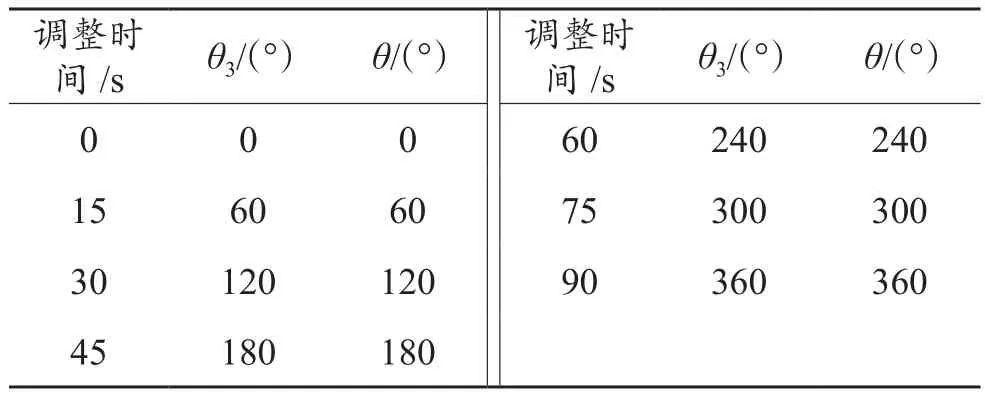
表6 內偏心環不轉動時外偏心環加速轉過角度與方位角的關系Table 6 Relationship between rotation angle and azimuth angle while the external eccentric ring is accelerated and the internal eccentric ring is not rotated

選取表6中的4數據，用牛頓插值法將選取的數據做出一個牛頓插值多項式

證明式（4）在旋轉外套旋轉的情況下也適用。

3.4.4 同時調節內偏心環和外偏心環對工具導向的影響 外套旋轉的情況下進行仿真實驗，讓內偏心環從 0°調整到 180°，外偏心環從 0°調整到 360°，偏心機構截面偏擺距離R從0變化到最大，得到的數據做出的圖與圖15一致，即與式（3）和式（4）聯合做出的圖一致。證明在外套旋轉的情況下，同時調節內外偏心環，式（1）和式（4）也適用。

4 結論

Conclusions

（1）通過仿真并運用牛頓插值法驗證了在外套旋轉和不旋轉2種情況下，調整導向軸偏置角β的公式的正確性，并得到了導向軸的運動軌跡。

（2）通過仿真運用牛頓插值法驗證了在外套旋轉和不旋轉2種情況下，調整導向軸方位角θ的公式的正確性，當β=0°時為特殊情況，并得到了導向軸的運動軌跡。

（3）通過仿真運用牛頓插值法驗證了在外套旋轉和不旋轉2種情況下，調整導向軸偏置角β的公式和調整導向軸方位角θ的公式聯合使用的正確性，并得到了導向軸的運動軌跡。

（4）通過仿真實驗，驗證了一種基于可控彎接頭鉆井工具偏心機構的控制方法的正確性。

［1］郭曉霞，楊金華，鐘新榮.北美致密油鉆井技術現狀及對我國的啟示［J］.石油鉆采工藝，2014，36（4）：1-5，9．

GUO Xiaoxia,YANG Jinhua, ZHONG Xinrong. The status of tight oil drilling technology in North America and its enlightenment to China［J］ . Oil Drilling & Production technology, 2014, 36（4）: 1-5, 9.

［2］李凱，高德利，宋執武. 定向井鉆井技術及可變徑穩定器應用研究［J］. 石油礦場機械，2011，40（7）：4-8.

LI Kai, GAO Deli, SONG Zhiwu. Application research of directional well drilling technology and variable gauge stabilizer［J］ . Mine in Oilfield Machinery, 2011, 40（7）:4-8.

［3］孫銘新. 旋轉導向鉆井技術［M］. 東營：中國石油大學出版社，2009.

SUN Mingxin. Rotary directional drilling technology［M］. Dongying: China University of Petroleum Press,2009.

［4］劉慶龍. 推靠式旋轉導向鉆井工具導向能力測試系統［J］. 化工自動化及儀表，2014，41（5）：575-579.

LIU Qinglong. Research on guidance ability test system of push-pull rotary directional drilling tools［J］. Chemical Process and Instrument, 2014, 41（5）: 575-579.

［5］BISCARO E, D’ALESSANDRO J D, ORENO A, HAHN M, LAMBORN R, AI-NAABI M H, BOWSER A C.New rotary steerable drilling system delivers extensive formation evaluation for high build rate wells［R］. SPE 174016, 2015.

［6］祝效華，劉少胡，聶榮國，湯歷平，敬俊，李禮. KWQ-216型地面可控井下變徑穩定器［J］. 石油鉆采工藝，2011，33（1）：120-122.

ZHU Xiaohua, LIU Shaohu, NIE Rongguo, TANG Liping, JING Jun. LI Li. KWQ-216 surface controlled downhole variable diameter stabilizer［J］. Oil Drilling& Production Technology, 2011, 33（1）: 120-122.

［7］劉新華，董廣華，趙洪山，楊全進. 旋轉導向井下工具控制系統設計及室內試驗［J］. 石油鉆探技術，2011，39（5）：86-90.

LIU Xinhua, DONG Guanghua, ZHAO Hongshan, YANG Quanjin. Design and laboratory test of control system for Rotary Steering Motor［J］ . Petroleum Drilling Technology, 2011, 39（5）: 86-90.

［8］劉英海，張光偉. 可控彎接頭偏心環摩擦及扭矩分析［J］. 機械研究與應用，2016，29（1）：57-59.

LIU Yinghai, ZHANG Guangwei. Friction and torque analysis on eccentric ring in controllable bent sub［J］ .Journal of Mechanical Research and Application, 2016, 29（1）: 57-59.

［9］祝效華，劉少胡，石昌帥，許建民. 基于CAE/CFD技術的套管防磨工具優化設計［J］. 石油鉆探技術，2010，38（2）：58-61.

ZHU Xiaohua, LIU Shaohu, SHI Changshuai, XU Jianmin. Optimization design of casing wear resistant tools based on CAE / CFD technology［J］ . Petroleum Drilling Technology, 2010, 38（2）: 58-61.

［10］張光偉，劉英海. 可控彎接頭導向控制理論研究［J］.西安石油大學學報（自然科學版），2016，31（3）：110-115.

ZHANG Guangwei, LIU Yinghai . Theoretical research of controllable sub steering control［J］. Journal of Xi'an Shiyou University（Natural Science Edition）,2016, 31（3）: 110-115.

［11］李志遠. 新型靜態偏置指向式旋轉導向執行機構導向控制研究［D］. 天津：天津大學，2013.

LI Zhiyuan. Steering control research on a new steering mechanism for static point-the-bit rotary steerable system［D］. Tianjin: Tianjin University, 2013.

［12］肖筱南. 現代數值計算方法［M］. 北京：北京大學出版社，2003：150-159.

XIAO Xiaonan. Modern numerical method［M］.Beijing: Peking University Press, 2003: 150-159.

［13］吳忠強，劉志新，魏立新，丁華鋒. 控制系統仿真及MATLAB語言［M］. 北京：電子工業出版社，2009：57-71.

WU Zhongqiang, LIU ZhiXin, WEI Lixin, DING Huafeng. Control system simulation and MATLAB language［M］. Beijing: Publishing House of Electronics Industry, 2009: 57-71.