抓住不變量思考

◎陳日銘

抓住不變量思考

◎陳日銘

有的百分數問題，題中有的量在變化，有的量卻始終不變。量在變化，數量關系就會隨著變化，給分析問題和解決問題帶來困難。如果我們抓住“不變量”去思考，就能收到奇效。

例1：六(1)班原來有55人，男生占全班人數的60%，后來調出了幾名男生去參加勞動，這時男生占全班人數的56%。這個班現在有學生多少人？

在這道題里，男生人數、男生人數占全班人數的百分數、全班人數等數量關系都在變化，且因調出的男生人數不明，以致其他幾個變量都無法求出。但仔細分析后，可以發現題中有一個量——女生人數始終沒有變，抓住這個不變量為突破口，即可求出其他未知量。首先求出這個班女生的人數：55×(1-60%)=22(人)，然后求出現在女生人數占全班人數的百分之幾，1-56%=44%，最后可求出這個班現有人數：22÷44%=50(人)。

例2：含鹽15%的鹽水20千克，要使鹽水含鹽10%，需加水多少千克？

含鹽15%的鹽水，要使它含鹽10%，水的重量增加，鹽的重量沒有變。抓住這個不變量，問題就可獲解。

含鹽15%的鹽水20千克時，鹽的質量算式為20×15%。要使鹽水含鹽10%時，設需加水x千克，那么這時鹽的質量算式為(20+)×10%。根據鹽的質量前后不變的等量關系，可得方程：

解這個方程得x=10

即需加水10千克。

例3：新力機器制造廠，原計劃每天生產40臺機器，20天可以完成。如果要提前4天完成，每天要完成原計劃日產量的百分之幾？

由題意可知，工作效率×工作時間=工作總量，工作總量是不變量，所以工作效率和工作時間成反比例。于是，可根據“實際工作效率×實際時間=計劃效率×計劃工作時間”的等量關系來解。設每天實際完成x臺，列方程得：

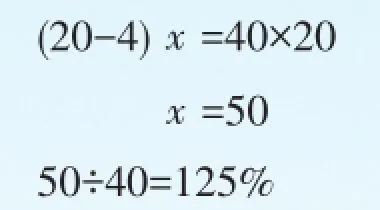
即每天完成原計劃日產量的125%。