一種新穎的差分混合蛙跳算法①

王 娜, 高學軍

?

一種新穎的差分混合蛙跳算法①

王 娜, 高學軍

(廣東工業(yè)大學應用數(shù)學學院, 廣州 510006)

在使用智能優(yōu)化算法處理函數(shù)優(yōu)化問題時, 保持種群的多樣性及加快種群的收斂速度可以提升一個算法的性能. 針對混合蛙跳算法在尋優(yōu)過程中易陷入局部最優(yōu)和早熟收斂的缺點, 本文提出了一種新穎的差分混合蛙跳算法. 該算法借鑒差分進化中的變異交叉思想, 在前期利用子群中其他個體的有用信息來更新最差個體, 增加局部擾動性, 以提高種群的多樣性; 在后期為加快收斂速度使用最好個體的信息進行變異交叉操作. 同時本文使用歸檔集進一步保留種群的多樣性. 仿真測試結果表明: 該算法在求解優(yōu)化問題時較基本蛙跳算法和平均值蛙跳算法具有更好的尋優(yōu)性能.

智能優(yōu)化; 混合蛙跳算法; 差分進化; 歸檔集

1 引言

混合蛙跳算法(SFLA)[1]是由Eusuff等人于2003年提出的一種模擬青蛙覓食過程的新的智能優(yōu)化算法. 該算法融合了模因演算算法(memetic algorithm, MA)和粒子群優(yōu)化算法(particle swarm optimization, PSO)兩者的優(yōu)點, 具有模型簡單、易于實現(xiàn)、控制參數(shù)少等優(yōu)點, 近年來已被成功應用于智能優(yōu)化領域[2-5]. 但相關實驗測試表明, SFLA雖具有局部精確搜索的特點, 卻因在尋優(yōu)過程只利用了全局最優(yōu)和子群最優(yōu)青蛙對子群最差青蛙更新使得算法前期容易陷入局部最優(yōu), 導致種群多樣性降低, 求解精度低, 后期收斂速度慢. 為了提高SFLA解決優(yōu)化問題的性能, 國內外學者對其進行了大量的研究. 如: Elbeltagi等人[6]將“認知分量”引入子群內部搜索策略中, 提高了算法的求解成功率, 一定程度上提高了算法的全局搜索能力; 趙芳等人[7]根據(jù)適應值所在范圍定義新的粒子分類標準避免了算法的盲目搜索, 通過動態(tài)調整慣性權重提高全局搜索能力, 并借用柯西變異算子跳出局部最優(yōu)的陷阱, 從而提高了算法的優(yōu)化性能; 張強等人[8]通過動態(tài)改變多樣性比例來改變子群最優(yōu)值的多樣性密度來增加種群多樣性.

本文在借鑒前人研究成果的基礎之上, 針對SFLA[9]易陷入局部最優(yōu)和收斂速度慢的缺點, 根據(jù)差分進化算法中的變異、交叉操作不僅能充分利用種群信息從而提高算法的多樣性, 同時還可以有效地提高算法的搜索速度的特點, 提出了一種新的更新策略, 在算法前期加入改進的差分算子rand-1來更新個體, 增加隨機擾動性, 提高全局搜索能力; 在算法后期, 加入差分算子best-rand-2來提高算法的收斂速度. 同時, 處理越界個體時對變化尺度進行動態(tài)調整, 改進了算法的尋優(yōu)精度. 而在每一代更新完成后, 引入歸檔集, 保存了好的被替代個體, 而被替代的這些個體可能包含有用的信息, 有助于收斂到最優(yōu)點, 從而保持了種群的多樣性. 仿真實驗測試結果表明, 改進后的差分蛙跳算法(記為DSFLA)較基本SFLA和基于平均值改進算法(記為SFLA-AV)而言, 新算法加快了收斂速度, 大大提高了求解精度, 說明了算法的有效性和可行性.

2 混合蛙跳算法

在已知定義空間中隨機產生個點組成初始化群體={1,2,...,X}, 第點的位置代表函數(shù)在可行域的一個解X=(x1,x2,..., x), 其中=1,2,...,,為解空間的維數(shù). 根據(jù)目標函數(shù)計算出所有青蛙的初始適應值并升序排序, 第一只青蛙記為種群的最優(yōu)青蛙X=(x1,x2,..., x). 然后, 把種群平均分為個子群, 每個子群有只青蛙,=×, 劃分原則為

式中,=1,2,...,,=1,2,...,. 每個子群分別用X=(x1,x2,..., x)、X=(x1,x2,..., x)來表示適應值最好的青蛙和適應值最差的青蛙. 在子群的每一次進化中, 對最差的青蛙X的位置進行調整, 其更新策略為:

青蛙移動的步長:

(1)

青蛙更新后的位置:

(2)

對子群最差青蛙X位置更新過程中, 如果更新策略產生一個較好的解, 則用新解X’更新X; 否則用種群最優(yōu)的青蛙X替換子群最優(yōu)青蛙X執(zhí)行公式(1)(2); 若仍沒有改進, 則從定義空間中隨機產生一個新解取代X, 這樣就完成了子群的一次進化. 所有子群按照這種更新策略更新最差個體, 直到子群迭代次數(shù). 然后各子群的所有個體重新混合, 計算適應值按升序排序后重新分組, 繼續(xù)進行局部搜索更新, 如此反復直到達到全局最大迭代次數(shù)或者滿足約束條件, 算法停止.

3 改進的差分混合蛙跳算法

3.1 引進差分算子更新策略

差分進化算法(differential evolution, DE)[10]是一類基于群體智能的啟發(fā)式隨機搜索算法. DE類似于遺傳算法, 存在變異、交叉和選擇等多種進化模式[11], 為提高種群的多樣性和算法的收斂速度, 本文在算法進化前期和后期分別借鑒了rand-1和best-rand-2兩種模式并進行了改進, 使得該算法比基本SFLA具有更好的尋優(yōu)性能.

在算法前期, 為保持種群的多樣性, 提高全局的搜索能力, 不是對子群中的最差個體更新, 而是隨機選取三個個體, 其中一個個體作為目標個體, 其他兩個個體用來更新移動步長, 借鑒差分變異操作[12]的思想, 引入改進的差分算子rand-1, 新的更新策略為:

, (3)

在算法后期, 為加快算法的收斂速度, 有助于收斂到最優(yōu)點, 用子群中最好的個體作為目標個體, 隨機選取兩個個體更新移動步長, 引入差分算子best-rand-2, 新的更新策略為:

(4)

引入改進的差分變異操作后, 為了進一步提高算法的局部搜索能力, 繼續(xù)保持種群的多樣性, 對產生的新個體X繼續(xù)執(zhí)行交叉操作[12], 改進后的交叉更新策略如下:

(5)

(6)

式子中,X為當前個體第維的值, 其中,1,2,...,;=1,2,...,;Ub、Lb分別指定義空間第維的上下界;指當前種群進化代數(shù),指種群進化最大代數(shù).

3.2 歸檔集

在子群進化的過程中, 有些被更新掉的個體可能包含有用的信息, 有助于算法收斂到最優(yōu)點, 因此在子群進化中加入歸檔集[13]可以保存被更新的最差個體. 歸檔集的具體操作: 在初始化的時候, 隨機產生2個個體, 建立歸檔集. 在每一個種群進化中, 每個子群更新次數(shù)內淘汰的個體中的一半隨機取代歸檔集里相同數(shù)目的個體. 歸檔集的使用進一步保持了種群的多樣性, 提高算法的全局搜索能力.

3.3 算法流程

改進的差分混合蛙跳算法具體的流程如下所示.

第一步: 設置相關參數(shù)種群規(guī)模=200, 解空間維數(shù)=5, 子群數(shù)=20, 子群內更新次數(shù)=10, 種群最大迭代次數(shù)為=100,=0.4,=0.5;

第二步: 隨機初始化種群的每只青蛙, 并根據(jù)目標函數(shù)計算每只青蛙的適應值;

第三步: 根據(jù)青蛙適應值對種群升序排序, 記錄第一只青蛙為種群的最優(yōu)青蛙;

第四步: 將種群按指定規(guī)則劃分為20個子群, 每個子群10只青蛙, 并記錄每個子群中最優(yōu)的青蛙和最差的青蛙;

第五步: 建立歸檔集, 隨機產生兩倍種群數(shù)量的青蛙, 并計算每只青蛙的適應值;

第六步: 按以下規(guī)則對每個子群獨立進化10次, 每一次子群進化完成后產生20個被淘汰的個體, 按適應值降序排序, 將前10個隨機取代歸檔集中的10個個體.

在種群迭代30%代以前, 根據(jù)差分算子rand-1按式子(3)更新得到新個體, 對新個體按式子(5)越界處理, 如果新個體的適應值優(yōu)于子群最差個體則替代之并按式子(4)進行交叉操作, 再次越界處理; 否則從歸檔集隨機選取三個個體按式子(3)進行更新得到新個體, 越界處理計算適應值, 如果新個體的適應值優(yōu)于子群最差個體則用新個體替代子群最差個體, 否則從歸檔集中隨機選一個替代之;

在種群迭代30%代以后, 根據(jù)差分算子best-rand-2按式子(4)更新并按式子(6)越界處理得到新個體, 如果新個體的適應值優(yōu)于子群最差個體則替代之并按式子(5)進行交叉操作并越界處理; 否則從歸檔集隨機選取兩個個體和子群最優(yōu)個體按式子(4)更新產生新個體并越界處理計算適應值, 如果新個體的適應值優(yōu)于子群最差個體則用新個體替代子群最差個體, 否則從歸檔集中隨機選一個替代之;

第七步: 是否達到子群最大迭代次數(shù), 是則完成一次種群迭代, 并將進行第八步, 否則返回第六步;

第八步: 混合子群中所有的青蛙, 重新形成一個完整的種群, 并按適應值升序排序, 記錄第一只青蛙為種群的最優(yōu)青蛙, 完成種群的一次更新, 判斷是否滿足終止條件, 是則輸出最優(yōu)青蛙Fbest的相關信息, 算法結束; 否則進行種群下一代更新, 跳轉第四步.

4 實驗結果及分析

4.1 測試函數(shù)與條件

為了驗證DSFLA的優(yōu)化性能, 本文選取五個典型的連續(xù)優(yōu)化函數(shù)進行測試, 并與基本混合蛙跳算法(SFLA)和基于平均值改進算法(記為SFLA-AV)作比較．

為了驗證DSFLA的優(yōu)化性能, 本文選取五個典型的連續(xù)優(yōu)化函數(shù)進行測試, 并與基本混合蛙跳算法(SFLA)和基于平均值改進算法[14](記為SFLA-AV)作比較．

其中1:Sphere Model是單峰函數(shù)、2:Rastr-igin Function、3:Schaffer1 Function、4:Griewand Function和5:Ackley Function都是復雜的多峰函數(shù), 它們的理論最優(yōu)值均為0. 算法的參數(shù)設置為: 種群規(guī)模=200, 解空間維數(shù)=5, 子群數(shù)=20, 子群內更新次數(shù)=10, 種群最大迭代次數(shù)為=100,=0.4,=0.5. 為減小偶然性對算法測試結果產生的影響, 每個算法均獨立運行30次后取平均值, 仿真結果如表1所示.

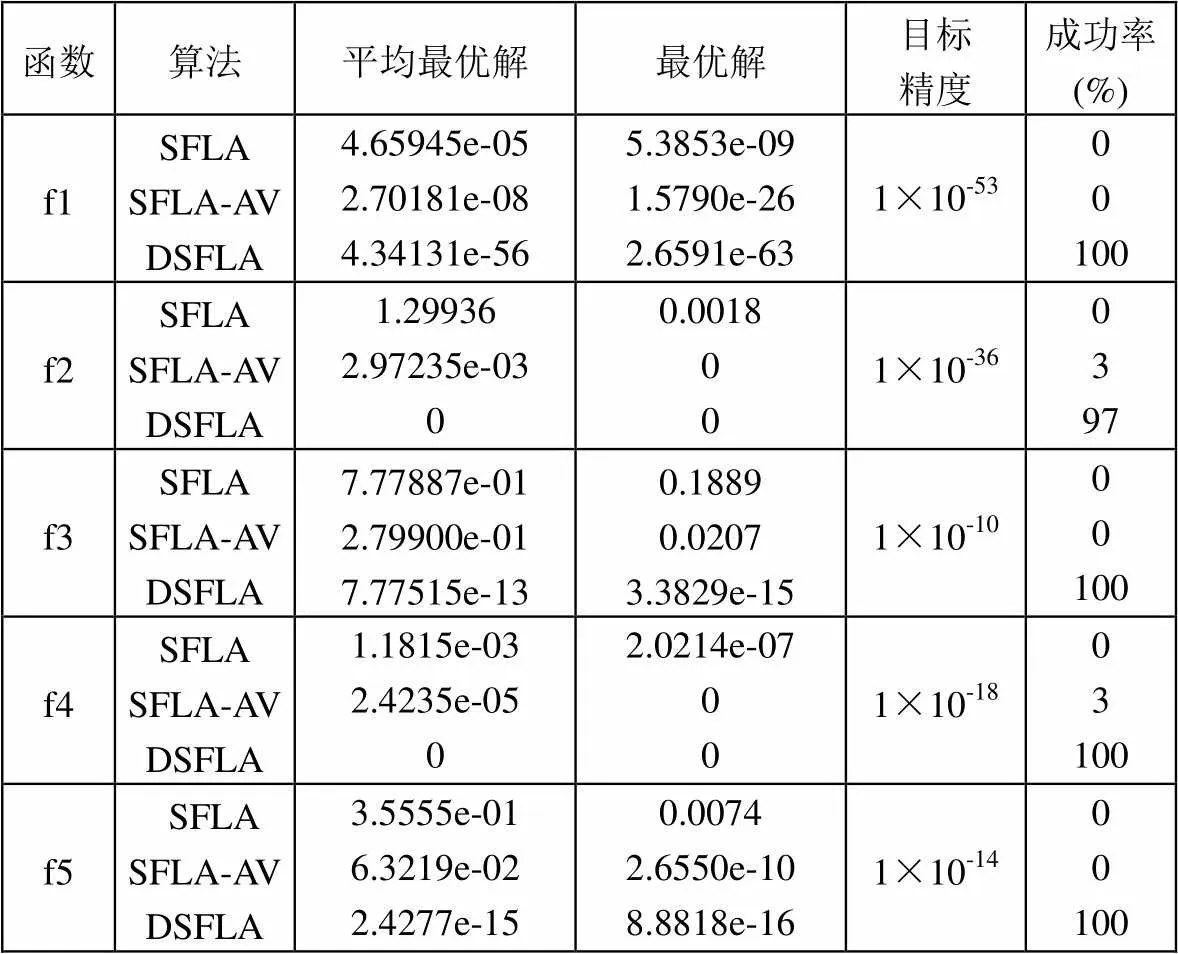
表1 計算結果

4.2 實驗結果和分析

從表1的求解結果對比看出: DSFLA的最優(yōu)解、平均值和求解精度及成功率都明顯優(yōu)于基本的SFLA和SFLA-AV, 說明DSFLA算法后期能進行更加精確的局部搜索, 具有更好的穩(wěn)定性. 就平均最優(yōu)解求解的精度來說, 在1,2,3,4,5函數(shù)中, DSFLA比SFLA分別提高了1×1051倍, 1×10∞倍, 1×1012倍, 1×10∞倍, 1×1014倍; DSFLA比SFLA-AV分別提高了1×1048倍, 1×10∞倍, 1×1012倍, 1×10∞倍, 1×1013倍, 說明DSFLA的求解精度得到有效的提高. 其中, 對于函數(shù)2,4, DSFLA均搜索出理論最優(yōu)解.

圖1~5為3種算法分別對5個典型的連續(xù)優(yōu)化函數(shù)搜索最優(yōu)解的進化曲線. 從圖中可以得到: SFLA和SFLA-AV在算法早期就陷入局部最優(yōu)的陷阱, 后期的收斂速度很慢, 幾乎跳不出局部最優(yōu)的陷阱, 而DSFLA在算法進化前期能很好的保持種群的多樣性, 提高全部的搜索能力, 在算法進化的后期, DSFLA的收斂速度加快, 具有能尋得高質量的最優(yōu)解的能力.

從表格數(shù)據(jù)和圖像的進化曲線都能表明DSFLA無論是在求最優(yōu)解的穩(wěn)定性上還是質量上都能明顯勝于SFLA和SFLA-AV, 證明了本文改進的算法是有效和可行的優(yōu)化算法.

5 總結

SFLA是一種新的智能尋優(yōu)算法. 本文借鑒差分變異的思想, 利用子群個體間的信息共享, 改進子群最差個體的更新策略, 不僅有效的提高了算法的全局尋優(yōu)能力和求解精度, 還加快了算法的收斂速度. 算法還通過加入歸檔集及動態(tài)調整越界個體的變化尺度來進一步保持算法的多樣性, 提高了優(yōu)化性能. 實驗仿真結果表明DSFLA的有效性和穩(wěn)定性.

1 Eusuff MM, Lansey KE. Optimization of water distribution network design using the shuffled frog leaping algorithm. Journal of Water Resources Planning and Management, 2003, 129(3): 210–225.

2 郭業(yè)才,張苗青.基于混合蛙跳算法的多模盲均衡算法.兵工學報,2015,36(7):1280–1287.

3 王茜,張粒子,舒雋,王楠.基于閾值選擇策略的改進混合蛙跳算法在電網(wǎng)規(guī)劃中的應用.電力系統(tǒng)保護與控制,2011, 39(3):35–39.

4 劉紫燕,唐思騰,馮麗,帥暘.混合蛙跳在AF協(xié)作通信功率優(yōu)化中的應用.計算機仿真,2015,32(7):190–310.

5 陳海濤,沈強.改進的蛙跳算法在云計算資源中的研究.計算機與數(shù)字工程,2015,(8):1382–1506.

6 Elbeltagi E, Hegazy T, Grierson D. A modified shuffled frog-leaping optimization algorithm applications to project management. Structure and Infrastructure Engineering, 2007, 3(1): 53–60.

7 趙芳,張桂珠.基于新搜索策略的混合蛙跳算法.計算機應用與軟件,2015,(8):224–228.

8 張強,劉麗杰,郭昊.一種保持種群多樣性的改進混洗蛙跳算法.計算機與數(shù)字工程,2015,(7):1175–1211.

9 Liong SY, Atiquzzaman M. Optimal design of water distribution network using shuffled complex evolution. The Institution of Engineers, 2004, 44(1): 93–107.

10 Rahnamayan S, Tizhoosh HR, Salama MMA. Opposition based dufferential evolution. IEEE Trans. on Evolutionary Computation, 2008, 12(1): 64–79.

11 賀毅朝,王熙照,劉坤起,王彥祺.差分演化的收斂性分析與算法改進.軟件學報,2010,21(5):875–885．

12 熊偉麗,陳敏芳,王肖,徐保國.運用改進差分進化算法辨識Hammerstein模型.南京理工大學學報,2013,37(4):536– 542.

13 王麗,劉玉樹,徐遠清.基于在線歸檔技術的多目標粒子群算法.北京理工大學學報,2006,26(10):883–887.

14 趙鵬軍,劉三陽.求解復雜函數(shù)優(yōu)化問題的混合蛙跳算法.計算機應用研究,2009,26(7):2435–2437.

Novel Differential Shuffled Frog Leaping Algorithm

WANG Na, GAO Xue-Jun

(Department of Applied mathematics, Guangdong University of Technology, Guangzhou 510520, China)

When using optimization algorithms to solve optimization problems, keeping the diversity of population and accelerating the convergence rate of the population can improve the performance of an algorithm. To overcome the main drawbacks of the shuffled frog leaping algorithm which may be easy to get stuck and premature convergence in a local optimal solution, this paper proposes a novel differential shuffled frog leaping algorithm. The algorithm is based on the idea of mutation crossover in differential evolution. In the earlier, it uses beneficial information of the other individuals in sub-group to update the worst individual, which increases the local disturbance and the diversity of population; in the later, the algorithm uses the best individual information to conduct the mutation and cross operation for speeding up the convergence rate of the population. Moreover, this paper uses the archive to keep the diversity of population. The experimental results show that the proposed algorithm is superior to the basic frog leaping algorithm and the average frog leaping algorithm in solving optimization problems.

optimization algorithm; shuffled leaping frog algorithm; differential evolution; archive

廣東省科技計劃(2013B051000075)

2016-04-22;收到修改稿時間:2016-06-12

[10.15888/j.cnki.csa.005563]