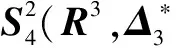)的局部支集樣條函數的構造方法
路 游,張麗娜,汪春曉
(中國石油大學(北京),北京 102249)
路 游,張麗娜,汪春曉
(中國石油大學(北京),北京 102249)
在計算幾何領域中,對于擬合、插值、重構,Box樣條函數已顯示出其重要的應用優勢,是一類應用廣泛的插值函數。但是在擬合算法中,大量的工作量是計算Box樣條基函數,因此,減少Box樣條函數的計算量,可以提高Box樣條的擬合速度。研究目的在于構造出具體的Box樣條函數的分段多項式形式,提高擬合算法的計算效率。首先,應用積分方法以及Box樣條的對稱性和輪換性分析Box的顯示表達式。然后,通過對七方向Box樣條在三維空間中進行Ⅲ-型剖分,在剖分上構造出三維空間中分段多項式形式的Box樣條的支撐函數,并且給出了具體的推導過程。最后實現了分段多項式形式的Box樣條函數。另外,由此支撐函數構造了擬插值算子和重構算法。通過此算法的數值實驗,在擬合算法效率上得到了預期的結果。
支撐函數;剖分;積分;胞腔;分段多項式
0 引 言
樣條函數是一種特殊的具有一定光滑性的分段函數,在計算機幾何與飛機、船舶制造等領域均有重要應用。1946年,數學家I.J.Schoenberg系統地建立了一元樣條函數的理論基礎[1]。從60年代開始,樣條函數得到了迅速的發展和應用。1966年,H.B.Curry和I.J.Schoenberg提出了一元B樣條函數,一種定義B樣條函數的幾何直觀方法[2]。1975年,以王仁宏為代表,采用函數論與代數幾何的方法,建立了任意剖分下的多元樣條函數的理論框架,并提出了光滑余因子協調法。1976年,de Boor將對一元B樣條的幾何解釋推廣到多元樣條。目前研究多元樣條的方法大致上分為三類。
(1)光滑余因子協調法,以王仁宏[3]為代表,在文獻[4]中也提出了三維非均勻空間中多元樣條函數構造方法。
(2)B-網方法,以Farin[5]為代表。
(3)B-樣條方法,亦稱投影子法,以Schoenberg[2]、de Boor[6]和Micchelli[7]等為代表。
近年來,對樣條函數進行了廣泛研究。文獻[8-10]介紹了多元樣條的應用研究,B樣條在模糊系統中的應用,將Box樣條應用到等值面可視化方法等。文獻[11-15]研究了B樣條的圖像插值方法、B樣條的數值流形和時間積分方法,同時研究了Box樣條與控制網之間的關系,得出了Box樣條與光滑拼接的Bezier曲面的充分條件,討論了Box樣條的體數據建模分析。另外,從向量的角度構造出三元Box樣條[16]和在隨機層面構造出特殊的隨機Box樣條[17],但都未給出Box樣條函數的具體表達式。
將一元樣條向多元樣條擴展的方法:張量積,將一元基函數通過張量積(乘積)得到多元樣條的基。但是,張量積形式的擴展方法存在一些缺點:首先,由一元B樣條基的張量積構造的基函數,使其參數域只能在矩形的區域上,而對于非規則的參數域,只能由經過剪裁和拼接的矩形域上的NURBS曲面得到。其次,張量積形式生成的基函數,使得生成的曲面次數升高,次數較高的曲面使運算變得復雜,甚至影響擬合曲面的幾何性質。而Box樣條作為非張量積函數,提供了一個完美的數學框架,其能構造一類具有可變的形狀和可變的局部的支集,它是進行各種重建或重構工作的有力工具。同時,在多元樣條函數的理論和應用中,Box樣條在對于給定剖分和指定的光滑度上,具有次數較低的分片多項式。
文中在總結樣條函數現有成果的基礎上,選擇廣泛采用的積分方法作為研究對象,主要利用Box樣條函數的顯示表達式和三維空間的Ⅲ-型剖分,通過積分方法構造樣條函數的計算機實現過程及機制。
1 Box樣條函數的積分方法
在三維空間R3中,設Δ為區域截斷菱形十二面體D?R3上的一個剖分區域,且Δ將區域D分為有限個胞腔。函數集合Cμ(μ=2)樣條函數,如果在每個胞腔中,多項式p的次數均不超過四次,即p∈Pk,則有:
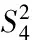
三元樣條在局部支集外取零值。如果它的支集最小,則一個非平凡的局部支集三元樣條即為一個Box樣條。
Bijk(x,y,z)=B(mx-i,ny-j,qz-k),i=0,1,…,n+1,j=0,1,…,m+1,k=0,1,…,q+1
1.1 三維Box樣條
在文獻[14]中,可以將二維空間的ZP元素推廣到三維空間的Box樣條。其中,二維樣條函數是由正方形及其四個方向的對角線形成,三維樣條函數是由立方體的三條邊和四條對角線所得。三維中七方向Box樣條表示為:
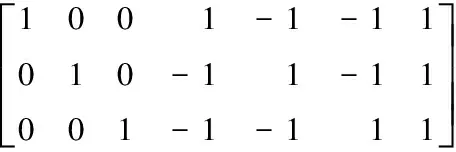
在三維七方向的Box樣條中,三坐標方向構成的Box樣條支集是一個立方體;四對角線方向構成的Box樣條支集是一個菱形十二面體(見圖1);七方向構成的Box樣條支集是一個被截斷的菱形十二面體(見圖2),其由立方體和菱形十二面體上指示函數的卷積生成,具體表達式為:
M(E1,E2)(x)=(ME1*ME2)(x)
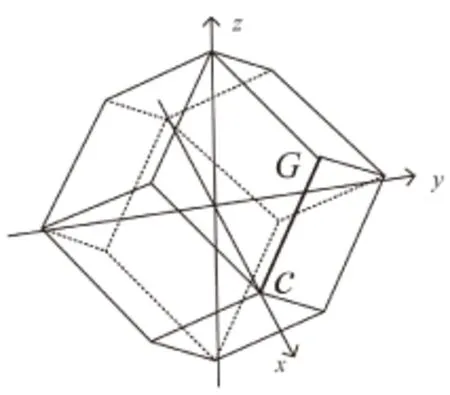
圖1 MΞ2的支集菱形十二面體
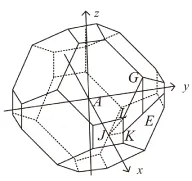
圖2 M的支集截斷菱形十二面體
1.2 B樣條的非組合積分構造方法
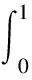
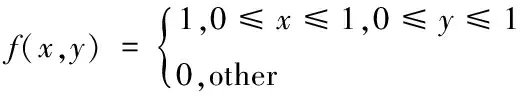
1.2.1 二元函數沿一個方向積分
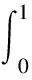
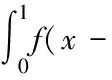
經過上面的轉換,很容易用定積分的知識得出積分結果。對于圖3中的點P(X,Y),與非零區域交于A,B兩點,則有:
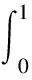
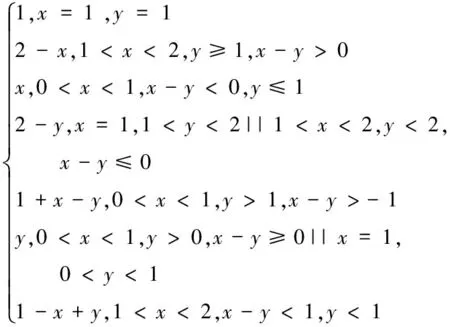
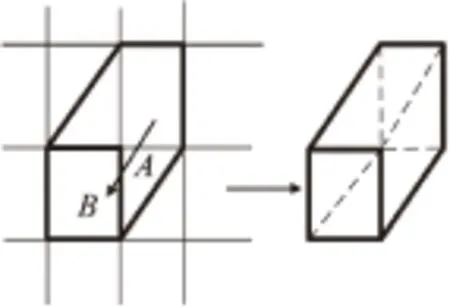
圖3 特征函數及ZP元素
1.2.2 二元函數沿兩個方向積分
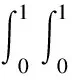
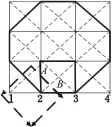
圖4 特征函數及ZP元素
這樣有:
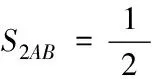
A(X,Y)=P(X,Y)+t1×(1,-1)
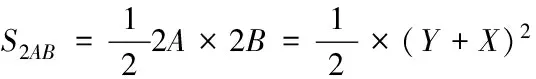
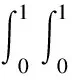
1.2.3 三元Box樣條函數積分
對于Box樣條的基函數[19]可由式(1)求出:
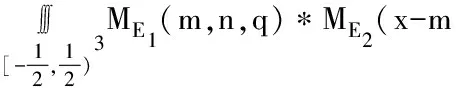
(1)
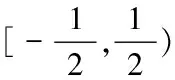
變量點(x,y,z)的取值范圍即為三維Box樣條的局部支集。同時,考慮ME2的表達式[7]:
ME2(x,y,z)=2max(0,1-max(|x|+|y|,|x|+|z|,|y|+|z|))
根據x,y,z在三維坐標中的對稱性,可將x,y,z映射到第一象限,則其在第一象限上可表示為:
ME2(x,y,z)=
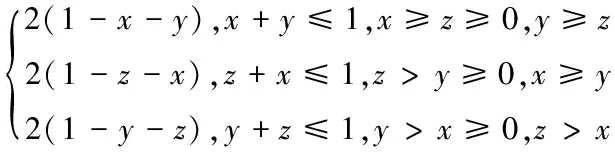
同樣地,根據x,y,z的輪換性,可將第一象限劃分成6部分(即為x≥y≥z≥0,y>x≥z≥0,y≥z>x≥0,z>y≥x≥0,z≥x>y≥0,x>z>y≥0),式(1)在區域x≥y≥z≥0上進一步表示為:
ME2(x,y,z)=2(1-x-y),x+y≤1,x≥y≥z≥0
(2)
那么,可在x≥y≥z≥0上對截斷十二面體進行Ⅲ-型剖分,剖分結果如圖5所示。則Box樣條函數的支撐域,截斷菱形十二面體即為菱形十二面體的指示函數ME2(x,y,z)與立方體[x-1/2,x+1/2)[y-1/2,y+1/2)[z-1/2,z+1/2)的指示函數常數1的卷積。
其中,限定x,y,z的范圍在一個剖分上(如圖5中13個剖分),各剖分為:
0≤z≤y≤x≤1/2
y≥z≥0,x≥1/2,x+y<1
z≥0,y≤1/2,x+z≤1,x+y≥1
x≥y>1/2,z≥0,x+z≤1
x≤1,z≤y≤1/2,x+z>1
x≤1,y>1/2,x+z>1,y+z≤1
x>1,y≥z,x+y≤2,y+z>1
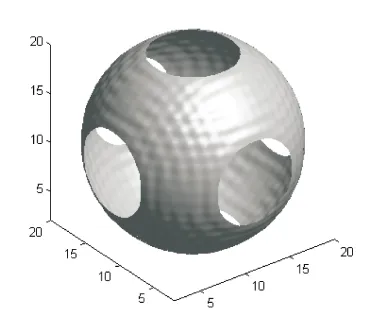
y>1/2,1 z≤y≤x≤1,y+z>1 y>1/2,0≤z≤x-1,x+y≤2 z≤y≤1/2,1 0≤z 0≤z≤y 圖5 剖分結果 可設Q為三維空間區域R3中以原點為中心,以(1,0,0),(0,1,0),(0,0,1),(-1,0,0),(0,-1,0)和(0,0,-1)為頂點的菱形十二面體。在三維非均勻的剖分上,連接正對的三個對角面可以得到一個四面體剖分x≥y≥z≥0。在此基礎上,該四面體繼續進行剖分,可得到如圖5的剖分結果,形成13個胞腔。 P1(x,y,z)=1/12 (9-24x2+16x3-24y2+24xy2+8y3-8xy3+4y4-24(-1+x) (-1+y)z2+4z4) P2(x,y,z)=1/24(17-48y2-48z2+8(x-9x2+8x3-2x4+6xy2+2y3-2xy3+y4+6(x+y-xy)z2+z4)) P3(x,y,z)=1/24(25+56x3-16x4-24x2(2+y)-48z2-8x(2-6y-3y2+2y3+6(-1+y)z2)+8(y(1+y)(-3+y2)+6yz2+z4)) P4(x,y,z)=1/3(3+7x3-2x4-3x2(2+y)-y(2+(-3+y)(-2+y)y)-6z2+6yz2+z4+x(-2+6z2+y(6+(3-2y)y-6z2))) P5(x,y,z)=1/24(37-12x4-24y2+8y3+8y4+24x2(y(-2+z)-2z)+8x3(4+y+z)+4z(-8-6z+z3)-8x(7+(-3+y)y(3+2y)-9z+6yz+3y(3+2y)-9(-1+y)z2+z3)+8y(-4+z(3+z(3+z)))) P6(x,y,z)=1/6(9-3x4-2y(3+(-3+y)(-2+y)y)+6x2(y(-2+z)-2z)-8z+6yz+6(-1+y)z2+2yz3+z4+2x3(4+y+z)-2x(7+(-3+y)z+6yz+3(-1+y)z2+z3)) P7(x,y,z)=1/6(12-16x+8x3-3x4-16y+24xy-12x2y+2x3y+4y3-2xy3-y4+2(-2+x+y)3z) P8(x,y,z)=1/6(-2+x+y)3(-2+x-y+2z) P9(x,y,z)=1/6(13+x4-2y(3+(-3+y)(-2+y)y)+6x2(-2+y)(-2+z)-8z+6yz+6(-1+y)z2+2yz3+z4+2x3(-4+y+z)-2x(15+(-3+y)y(3+2y)-9z+6yz+3(-1+y)z2+z3)) P10(x,y,z)=1/3(-1+x-y)(-2+x+y)3 P11(x,y,z)=1/24(53-32y-32z+4(x4+2y2(-3+y+y2)+6x2(-2+y)(-2+z)+6yz+6(-1+y)z2+2yz3+z4+2x3(-4+y+z)-2x(15+(-3+y)y(3+2y)-9z+6yz+3(-1+y)z2+z3))) P12(x,y,z)=1/24(65+8x4-72x2(-2+y)+8x3(-7+2y)-8x(-2+y)2(5+2y)+8y(-5+y(-3+y+y2)) P13(x,y,z)=1/24(3-2x)4 其他多項式可由上述多項式按對稱原則和輪換原則得到。 設局部支集函數B(x,y,z)是定義在R3上的函數,在區域Q之外取零值,其在每個胞腔上的表達式為pi(x,y,z)。那么,Box樣條的局部支集函數在三維空間中具有二階連續偏導數,即:B(x,y,z)∈C2(R3),且在Q內恒正。因此,B(x,y,z)是關于圖5剖分的三元Box樣條。 (1)數據準備。 對三維空間中散亂數據點可組成一個三維矩陣A,作為輸入數據點。 從上面的推導過程可得出非組合積分方法,構造分段多項式形式的Box樣條支撐函數算法如下: ①按照圖5所示對四面體進行編號,共有13個非零區域,編號從1~13。編號原則是按照四面體中的點引出的積分向量構成的區域,與初始非零正方形區域交點的位置一致性來劃分。 ②對四面體區域Δi計算從區域中的點引出的兩個向量構成的區域與非零正方形的交點,進而求出公共面積上的表達式。 ③四面體區域Δi編號加1,如果小于13且大于2則繼續,否則完成退出。 將上面積分方法構造出的局部支集函數,運用到多面體的構造中去。對于給定的輸入數據點,映射到區域x≥y≥z≥0上,根據對稱后所在的胞腔,代入Box樣條分段多項式,求解輸入點的樣條基函數。為簡便,將Δmnq在區域Q上的剖分仍記作Δmnq,設: Bijk(x,y,z)=B(mx-i,ny-j,qz-k) (3)構造擬插值算子。 三維空間中的三變量非張量積Box樣條可表示為: 其中,擬插值算子[4]為: (4)繪制等值面。 (5)分析擬合算法中,求解輸入數據點樣條基函數的時間復雜度。 以散亂數據點組成的41*41*41三維矩陣A,作為輸入數據點,對擬合出的80*80*80三維矩陣A,在處理器PIV-2.10GHz,內存為4.0GB的普通個人電腦上繪制任意形狀的等值面,結果如圖6所示。 通過上述算法的程序實現分析,已知n個數據點,設p為三維空間中一個點映射到區域x≥y≥z≥0上的時間,q為一個點代入多項式求值的時間,則求解數據點樣條基函數的時間可表示為: f(n)=n*p*q (3) 圖6 曲面x2+y2+z2-1等值面 對式(3)分析可知,其時間復雜度與數據點的個數以n增長,所以該算法求解數據點的Box樣條函數基函數的時間復雜度為Θ(n)。 與一般乘積形的B樣條相比,首先,在每一塊胞腔上的多項式次數是四次,且在邊界上具有二階光滑度。而乘積形樣條,三個一元二次B樣條相乘,不具有光滑度;三個一元二次B樣條相乘,其在剖分上的多項式次數是六次,而文中構造出的Box樣條在相同的光滑度的情況下,每塊胞腔上的次數較多,增加了運算量。其次,文中的Box樣條擬合的圖形真實感與乘積形B樣條繪制的相同。 文中通過應用積分方法構造了Ⅲ-型剖分上的Box樣條的支撐函數,并利用Box樣條的對稱性和輪換性,推導出三維空間中的Box樣條支撐函數顯式表達式,且給出了具體的推導過程。 在擬合算法中,大量的工作量是計算Bijk(x,y,z)。如果對每個數據點直接進行卷積計算,顯然此方法存在一些不足。首先,數值積分的計算都有誤差;其次,由于需要對輸入的每個數據點進行數值積分,在運算效率上比較低。而文中算法采用Box樣條支撐函數解析表達式進行計算。在效率上,避免了大量的重復積分,大大提高了Box樣條的擬合速度。 [1]SchoenbergIJ.Contributionstotheproblemofapproximation ofequidistantdatabyanalyticfunctions[J].QuarterlyAppliedMathematics,1946,4:45-99;112-141. [2]CurryHB,SchoenbergIJ.OnPolyafrequencyfunctionsIV:thefundamentalsplinefunctionsandtheirlimits[J].JAnalyseMath,1996,17(1):71-107. [3] 王仁宏.多元齒的結構與插值[J].數學學報,1975,18(2):91-106. [5]FarinG.BezierpolynomialsovertrianglesandtheconstructionofpiecewiseC’polynomials[D].Brunel:Univ.ofUxbridge,Middlesex,1980. [6]deBoorC.SplineaslinearcombinationofB-splines[M]//LorenzGG,ChuiCK,ShumakerLL.ApproximationTheoryII.NewYork:AcademicPress,1976:1-47. [7]DahmenW,MicchelliCA.Recentprogressinmultivariatesplines[M]//ApproximationtheoryIV.NewYork:AcademicPress,1983:27-121. [8] 郭慶杰.多元樣條若干理論與應用研究[D].大連:大連理工大學,2015. [9] 譚彥華,李洪興,馬秀娟,等.B樣條函數在模糊系統中的應用[J].控制理論與應用,2013,30(11):1445-1456. [10] 劉 曉,方美娥,張 楠.基于7方向Box樣條的等值面可視化[J].杭州電子科技大學學報,2015,35(5):63-67. [11] 魏曉靜.基于B樣條函數的圖像插值方法研究[D].大慶:東北石油大學,2014. [12] 溫偉斌.基于B樣條插值的數值流形方法與時間積分方法的研究[D].重慶:重慶大學,2014. [13]ZengXiaoming,ZhouGuorong,YangLianqiang.Bestboundsonthedistancebetween3-directionquarticboxsplinesurfaceanditscontrolnet[J].AppliedMathematics:AJournalofChineseUniversities,2013,28(2):147-157. [14] 楊聯強,王 東.三元四次箱樣條曲面與Bezier曲面的光滑拼接[J].計算機工程與應用,2013,49(23):119-121. [15]FangMeie,LuJia,PengQunsheng.Volumetricdatamodelingandanalysisbasedonseven-directionalboxspline[J].ScienceChinaInformationScience,2014,57(6):1-14. [16] 李 玲,路 游.三元Box樣條構造方法的實現[J].計算機技術與發展,2009,19(11):45-48. [17] 于 巍.一類隨機Box-樣條的逼近問題[J].甘肅聯合大學學報:自然科學版,2010,24(5):14-15. [18]deBoorC.Boxsplines[M].NewYork:Springer-VerlagInc.,1993. [19]EntezariA,MollerT.ExtensionsoftheZwart-PowellboxsplineforvolumetricdatareconstructionontheCartesianlattice[J].IEEETransactionsonVisualizationandComputerGraphics,2006,12(5):1337-1344. LU You,ZHANG Li-na,WANG Chun-xiao (China University of Petroleum-Beijing,Beijing 102249,China) In the field of computation geometry,for fitting,approximation,reconstruction,Box spline has showed its important application advantages and it is a kind of widely used interpolation function.But in the fitting algorithm,a large amount of workload is to calculate the Box spline.Therefore,the method of improving the fitting speed of Box spline is to reduce the calculation of it.The purpose of the research is to construct the polynomial form of the Box spline function,and improve the efficiency of the algorithm.By 3-partition in the three-dimensional space,the integration method and the symmetry and rotation of Box spline are used firstly to analyze its explicit form.And then the Box spline in polynomial form is constructed in the type-3 partition.Finally,the piecewise polynomial form of Box spline function is realized.Besides,the specific procedure is given.In addition,by using the support function,quasi-interpolation operators and reconstruction algorithm are constructed.Through the numerical experiments,the expected results are obtained in the efficiency of fitting algorithm. support function;partition;integration;cell;piecewise polynomial 2016-03-01 2016-06-09 時間:2016-11-22 國家自然科學基金資助項目(60873093) 路 游(1957-),男,博士,副教授,研究方向為計算幾何、圖形學、虛擬現實;張麗娜(1989-),女,碩士研究生,研究方向為計算機可視化。 http://www.cnki.net/kcms/detail/61.1450.TP.20161122.1227.012.html TP391.7 A 1673-629X(2017)02-0110-06 10.3969/j.issn.1673-629X.2017.02.025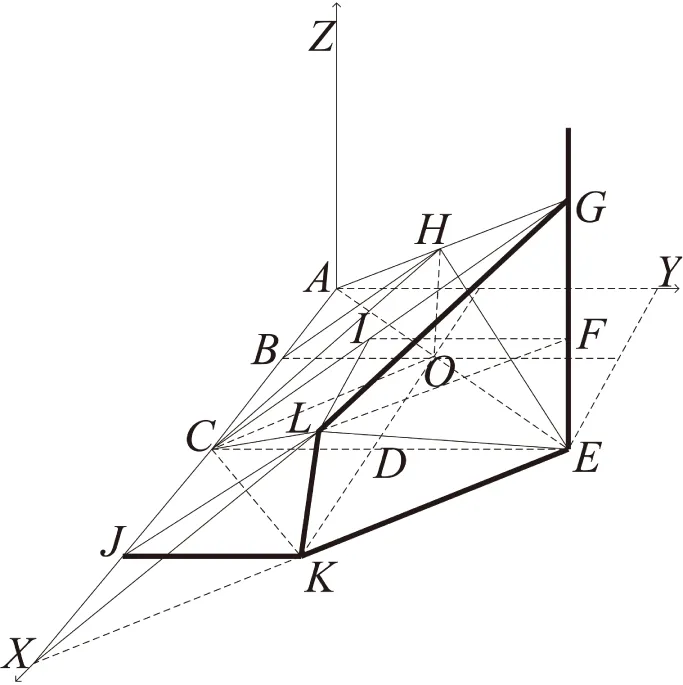
2 三元Box樣條的局部支集函數
3 空間體的擬插值算法
4 實驗結果
5 結束語