含兩個時間分數階導數的二維反常擴散方程求解與微分階數反演

王鳳丹，孫春龍，李功勝，賈現正

(山東理工大學 理學院，山東 淄博 255049)

含兩個時間分數階導數的二維反常擴散方程求解與微分階數反演

王鳳丹，孫春龍，李功勝，賈現正

(山東理工大學 理學院，山東 淄博 255049)

對于一類含兩個時間分數階導數的二維反常擴散方程,基于對時間分數階導數在Caputo意義下的離散,得到一個有限差分格式;利用分離變量法與Laplace變換得到該問題的解析解,并將兩種方法得到的解進行數值比較.進一步,給定終值時刻數據,應用同倫正則化算法對擴散方程中的兩個時間微分階數進行數值反演,并給出反演算例.數值結果表明隨著數據擾動水平的降低,解誤差逐步變小,所用的反演算法對微分階數反問題是有效的.

時間分數階導數；二維分數階擴散；解析解；微分階數反問題；數值反演

近年來,反常擴散模型的應用越來越廣泛.分數階擴散方程在大氣污染、水文地質學、金融學、物理學、力學、生物醫學工程等諸多領域有了若干非常成功的應用[1],分數階擴散模型相比經典的整數階高斯擴散模型能更好的模擬擴散過程和重建試驗數據.分數階導數具有記憶性、遺傳性和整體性,特別對于污染物長距離傳輸時表現出的非對稱、非線性的整體性行為模式的研究,分數階擴散模型可能是一個很有效的研究工具[2].對于含多個時間分數階擴散方程正問題的研究,劉發旺和Meerschaert[3]等人,研究了含多個時間分數階擴散-波動方程的數值計算方法,給出了隱式差分格式,并證明了隱式差分近似的無條件穩定性和收斂性. Luchko[4]應用分離變量法與傅里葉變換研究了一類含多個時間分數階擴散方程的解析解,并證明了解的唯一性.Gejji[5]等利用分離變量法推導出了一維非齊次和二維齊次時間分數階擴散-波動方程在齊次混合邊值條件下的解析解.

對于分數階擴散方程反問題的研究,越來越受到人們的關注. 鄭光輝和魏婷[6-7]等應用傅里葉正則化,研究了帶形區域上空間分數階擴散方程的逆時問題,同時考慮了空間分數階擴散方程中的源項反演問題,并且應用Tikhonov正則化對反問題數值求解.李功勝等[8]利用最佳攝動量算法對于一維時間分數階擴散方程的微分階數與擴散系數進行了數值聯合反演. 劉繼軍等[9]應用準可逆性正則化方法探討了一個時間分數階擴散中由終值數據確定初始分布的逆時反問題.

目前,關于高維分數階擴散方程相關反問題的研究還不多見.本文主要探討含兩個時間分數階導數的二維時間分數階齊次擴散方程的微分階數反演問題.對于正問題的求解,通過對時間分數階導數的數值離散,建立了一個隱式差分格式；同時利用分離變量法與Laplace變換得到該問題的解析解. 在正問題求解的基礎上,給定終值時刻數據為附加數據，考慮一個確定擴散方程中兩個時間微分階數的反問題.應用同倫正則化算法進行數值反演,并討論初始迭代、擾動水平等因素對反演算法的影響.

1 正問題及其數值解

考慮矩形域Ω=(0,l1)×(0,l2)上的二維時間分數階齊次擴散方程的初邊值問題：

(1)

其中(x,y)∈Ω,t>0,D>0是擴散系數,α,β∈(0,1)是時間分數階導數的階數,方程中的時間分數階導數均用Caputo的定義，分別為：

下面給出數值求解二維問題(1)的一個隱式差分格式.

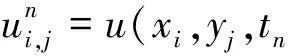
(2)

(3)

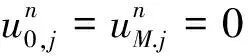
利用通常的差分離散方法,方程中的整數階導數項可以進行以下近似：

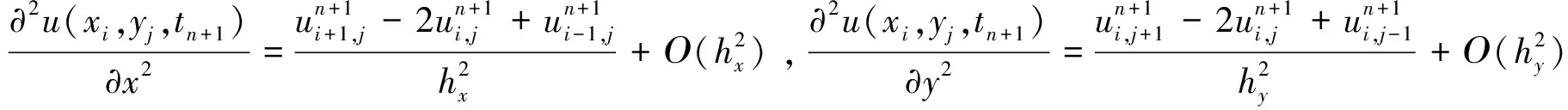
則原方程可以離散為

(4)

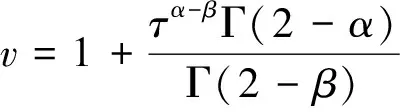
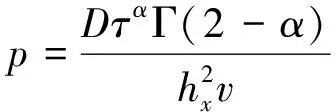
(5)

如果令ck=dk-1-dk,k=1,2,…,n，則差分格式可以進一步整理為矩陣形式為

(6)

其中

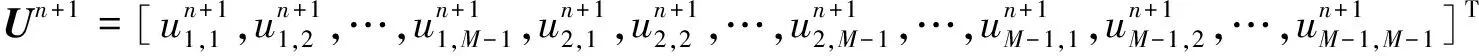
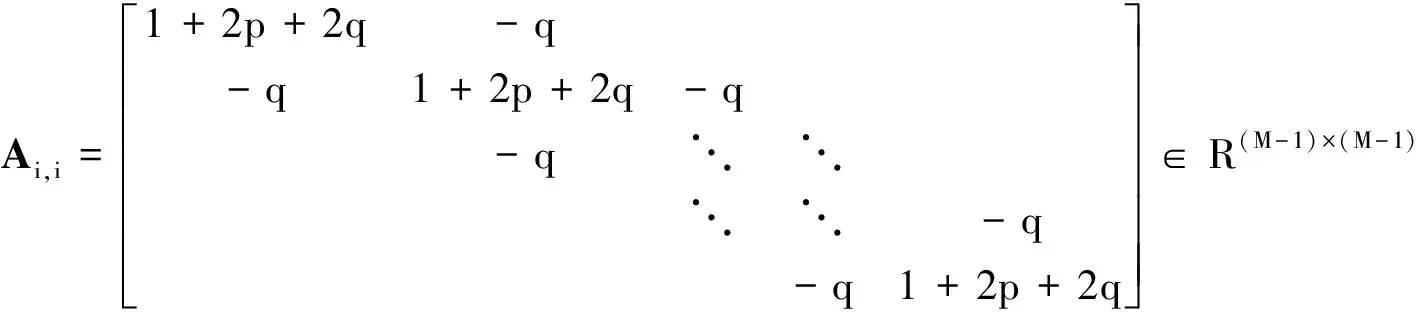
(7)

i=1,2,…,M-1; I為(M-1)×(M-1)階單位矩陣.

2 正問題的解析解

本節應用分離變量法和拉普拉斯變換,給出正問題(1)的基于Mittag-Leffler函數的解析解表達式,并進行數值模擬.

設u(x,y,t)=X(x)Y(y)T(t),代入方程可得

(8)

對式(8)整理可得

(9)

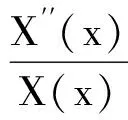
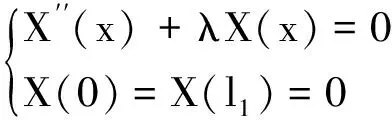
(10)

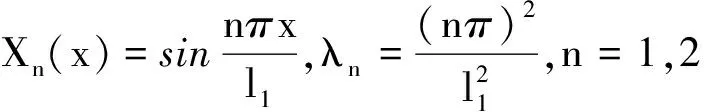
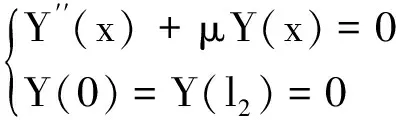
(11)

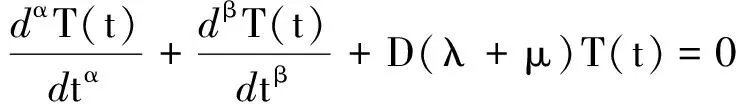
(12)

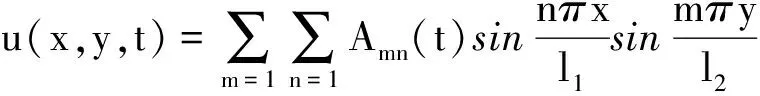
(13)

對t作Laplace變換可得

(14)

將式(14)代入式(13)中有：

(15)

(16)

令c=D(λn+μm)(常數).

(17)

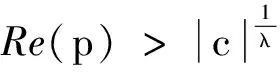
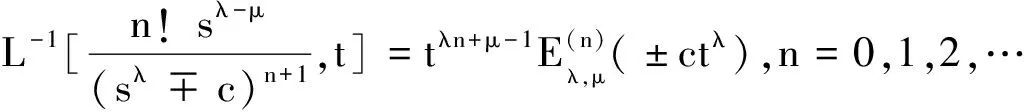
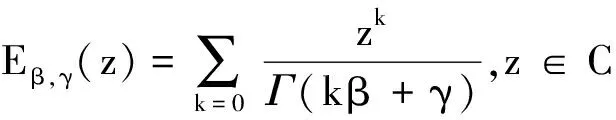
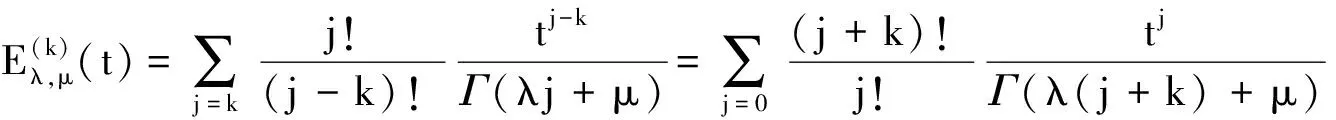
由引理1，即有

于是，可得

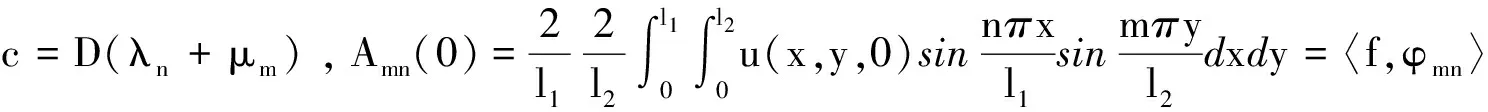
(18)

3 正問題的數值模擬

取l1=l2=π,T=1,擴散系數D=0.5,初始函數u(x,y,0)=sinxsiny,微分階數取為α=0.8,β=0.6,則由式(18),問題(1)的解析解可以表示為

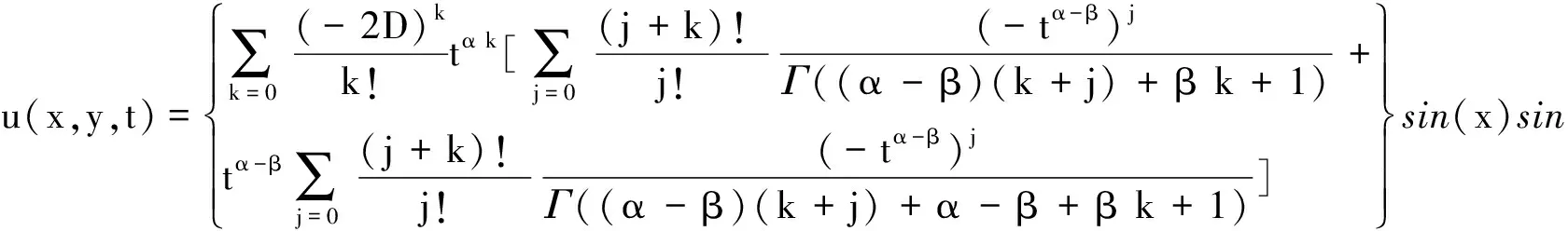
應用差分格式(6)進行數值計算,得到的數值解記為u*(x,y,t),解析解與數值解的誤差表示為Err=‖u(x,y,t)-u*(x,y,t)‖2/‖u(x,y,t)‖2.不同時間步長和空間步長的計算結果列于表1、表2.

表1 時間步長與解誤差(T=1)

Δt1/501/1001/200Err3．26654×10-23．31394×10-23．34039×10-2

表2 空間步長與解誤差(T=1)

hx=hyπ/10π/20π/50Err6．06776×10-23．31394×10-21．35194×10-3

表1、表2的計算結果表明，在當前算法下數值解能夠較好地吻合精確解,時間步長變化對解誤差影響不大,而隨著空間步長的減小,解誤差逐步減小.

進一步,取空間步長hx=hy=π/20,時間步長τ=1/100,數值解與解析解在t=T時的圖像繪于圖1.

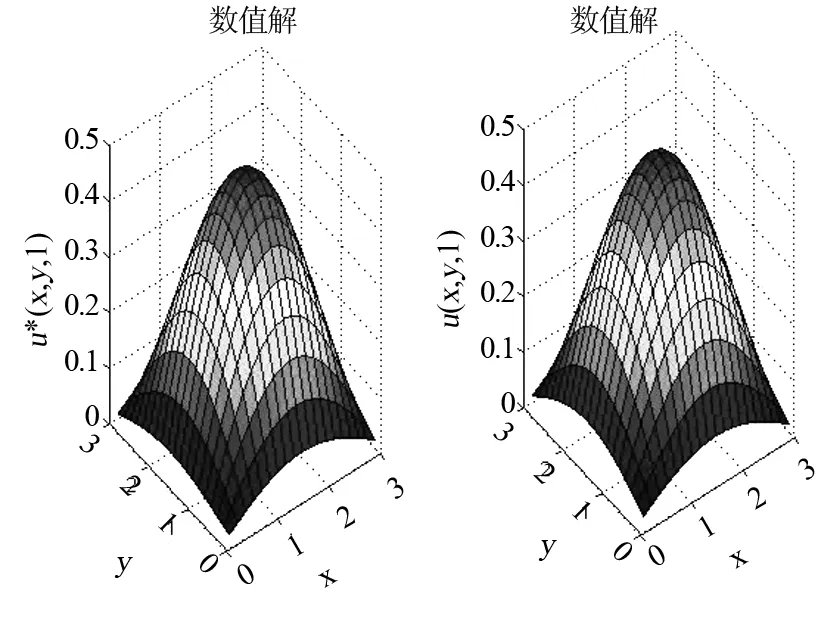
圖1 α=0.8,β=0.6,t=T時的數值解與解析解

4 確定微分階數的反問題與數值反演

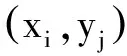
(19)

則由正問題(1)聯合(19)式構成了一個確定微分階數α和β的反問題.

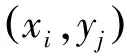
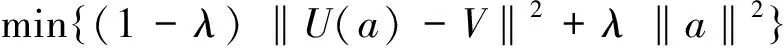
(20)

其中λ∈(0,1)為同倫參數.當待確定的未知量為常數時,同倫正則化算法過程主要包括迭代逼近、線性化近似、梯度近似與同倫正則化逼近等,而影響算法實現的主要因素是初始迭代、梯度近似中的微分步長、同倫參數、迭代精度或迭代次數以及正問題的計算精度等,具體步驟參見文[11-12]等,且選取同倫參數為

(21)

其中n是迭代次數,n0是當前同倫參數取值下降至0.5時的預估迭代次數,而β0>0是校正參數.下面給出數值反演算例.

設微分階數的真值為αtrue=[0.8,0.6].模型中其他參數取值同于第3節相應正問題數值算例中的取值, 且式(21)中的預估迭代次數與校正參數分別取為n0=5,β0=0.8.我們主要考察初始迭代與數據擾動對反演算法的影響.

首先看初始迭代對反演算法的影響,反演計算結果列于表3,其中a0表示初始迭代,ainv表示反演解,Err=‖ainv-atrue‖2/‖ainv‖2表示反演解與真解的誤差.

表3 初始迭代對反演結果的影響

a0ainvErr(0，0)(0．80000000，0．59999999)3．134×10-13(0．2，0．1)(0．80000000，0．60000000)2．982×10-14(0．5，0．3)(0．80000000，0．60000000)8．385×10-14(1．0，1．0)(1．5，1．3)(2．0，2．0)(0．79999999，0．60000000)(0．60000000，0．80000000)發散2．698×10-132．828×10-1

從表3可以看出,初始迭代的選取對反演結果有一定的影響.當其逐漸遠離真值時,反演解與真解的誤差變大.

其次,考察數據擾動水平對算法的影響.設帶擾動的附加數據表示為:

(22)

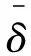
表4 擾動水平對反演結果的影響

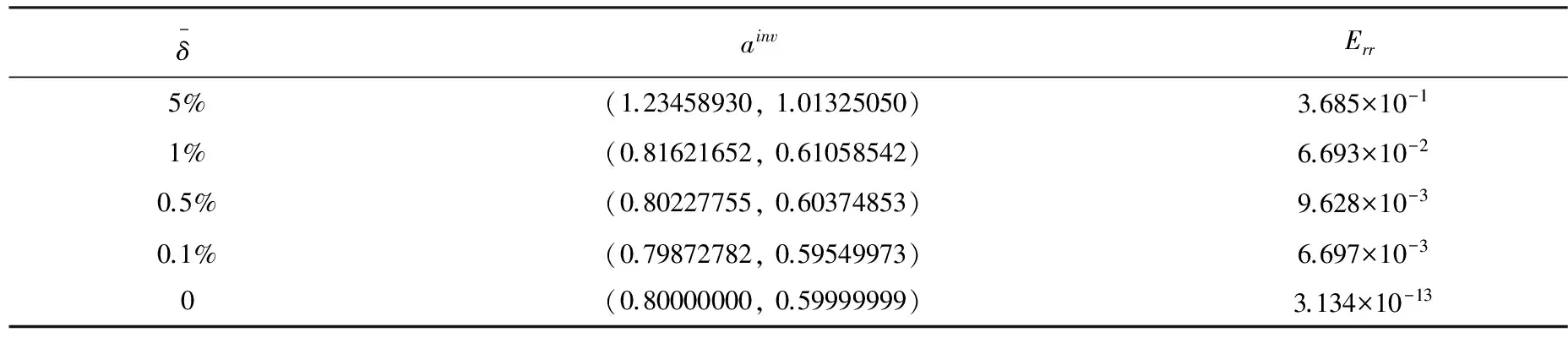
δ-ainvErr5%(1．23458930，1．01325050)3．685×10-11%(0．81621652，0．61058542)6．693×10-20．5%(0．80227755，0．60374853)9．628×10-30．1%0(0．79872782，0．59549973)(0．80000000，0．59999999)6．697×10-33．134×10-13

從表4可以看出,隨著數據擾動水平的減小,反演解與精確解的誤差逐漸減小,在不加擾動時,反演解幾乎接近真解,表明了反演算法的數值穩定性.

5 結束語

本文給出了含兩個時間分數階導數的時間分數階二維齊次擴散方程正問題求解的差分格式與解析解,并應用同倫正則化算法進行了微分階數的數值反演.反演結果表明,當數據擾動水平減小時,反演解與真解的誤差變小;當沒有擾動時,反演解與真解吻合.當擾動水平大于5%時,解誤差變大,這表明所討論的微分階數反問題具有一定的病態性.在數據有較大擾動時,構建更有效的反演算法是今后的一項主要工作.

[1]曹建雄. 分數階擴散方程的有限差方法及其應用[D]. 上海：上海大學, 2015.

[2]陳文, 孫洪廣, 李西成,等.力學與工程問題的分數階導數建模[M]. 北京：科學出版社, 2010.

[3]LIUF,MEERCHAERTMM,MCGOUGHRJ,etal.Numericalmethodsforsolvingthemulti-termtime-fractionalwave-diffusionequation[J].FractionalCalculus&AppliedAnalysis, 2013, 16(1):9-25.

[4]LUCHKOY.Initial-boundary-valueproblemsforthegeneralizedmulti-termtime-fractionaldiffusionequation[J].JournalofMathematicalAnalysis&Applications, 2011, 374(2):538-548.

[5]DAFTARDAR-GEJJIV.Positivesolutionsofasystemofnon-autonomousfractionaldifferentialequations[J].JournalofMathematicalAnalysis&Applications, 2005, 302(1):56-64.

[6]ZHENGGH,WEIT.SpectralregularizationmethodforaCauchyproblemofthetimefractionaladvection-dispersionequation[J].Mathematics&ComputersinSimulation, 2010, 233(10):2631-2640.

[7]ZHENGGH,WEIT.TworegularizationmethodsforsolvingaRiesz-Fellerspace-fractionalbackwarddiffusionproblem[J].InverseProblems, 2010, 26(11):115017.

[8]谷文娟, 李功勝, 殷鳳蘭,等. 一個時間分數階擴散方程的參數反演問題[J]. 山東理工大學學報(自然科學版), 2010, 24(6):22-25.

[9]LIUJJ,YAMAMOTOM.Abackwardproblemforthetime-fractionaldiffusionequation[J].ApplicableAnalysis, 2010, 89(11):1 769-1 788.

[10]PODLUBNYI.FractionalDifferentialEquations[M].SanDiego:Academicpress,1999.

[11]孫春龍, 李功勝, 賈現正,等. 含三個時間分數階導數的反常擴散方程求解與微分階數反演[J]. 山東理工大學學報(自然科學版), 2015, 29(3):1-7.

[12]賈現正, 張大利, 李功勝,等. 空間-時間分數階變系數對流擴散方程微分階數的數值反演[J]. 計算數學, 2014, 36(2):113-132.

(編輯：姚佳良)

The solution to the 2D two-term time-fractional diffusion equation and numerical inversion for the fractional orders

WANG Feng-dan, SUN Chun-long, LI Gong-sheng, JIA Xian-zheng

(School of Science, Shandong University of Technology, Zibo 255049, China)

A finite difference scheme is introduced to solve the 2D two-term time-fractional diffusion equation based on Caputo′s discretization to the time fractional derivatives. Using the method of separation of variables and Laplace transform, analytical solution to the forward problem is obtained, and numerical test is presented to compare the finite difference solution with the analytical solution. Furthermore, the homotopy regularization algorithm is applied to solve the inverse problem of determining the fractional orders given additional data at the final time. Numerical inversions with noisy data are performed, and the inversion solutions error becomes small as the noise level goes to small demonstrating the effectiveness of the proposed algorithm.

time fractional derivative;2D fractional diffusion; analytical solution; inverse problem of fractional order; numerical inversion

2016-05-18

國家自然科學基金項目(11371231, 11071148)

王鳳丹,女,949752533@qq.com; 通信作者：李功勝，男，lgs9901@163.com

1672-6197(2017)02-0001-07

O175

A