基于改進共軛梯度算法的二維PSD非線性修正

史春玉,李田澤,仝其豐，鄭 薇

(山東理工大學 電氣與電子工程學院, 山東 淄博 255049)

基于改進共軛梯度算法的二維PSD非線性修正

史春玉,李田澤,仝其豐，鄭 薇

(山東理工大學 電氣與電子工程學院, 山東 淄博 255049)

分析了二維PSD的非線性特征及其誤差產生的原因,總結了二維PSD的非線性特性對測量結果的不利影響,提出了改進的神經網絡共軛梯度算法,利用目標函數的梯度逐步產生共軛方向，并運用函數的導數方法進行快速搜索和插值運算.通過Matlab仿真,證明了該算法在不增設備復雜程度的前提下,提高了PSD邊緣區域的線性度、測量數據的準確性及測量速度,擴展了PSD在精密測量領域的應用.

位置敏感器件；共軛梯度算法；非線性修正

半導體光電位置敏感器件(Position Sensitive Detector，PSD)是一種高精度光電位置檢測傳感器件,它可以直接測量入射至其光敏面上的光束位置.它是一種對感光平面上入射點位置敏感的器件,即當入射光點落在器件感光面上的不同位置時,將相應的輸出對應的電信號,通過對這個輸出的電信號進行處理,則可確定入射光點在器件感光面上的位置[1].PSD是連續型模擬器件,像元大小不會影響其分辨率,因此可以達到很高的分辨率.PSD在高精確度非接觸式的位置測量場合有著其特有的優勢,在航空對接、精密測量、振動測量等領域獲得了廣泛的應用.但是由于其結面電阻的不均勻性、電極結構的差異性、背景光的不均勻性等因素,導致PSD存在較大的非線性誤差,其輸出的坐標不能精確反映入射光點的正確位置,使得PSD成為系統提高精度的難點[2].改善PSD非線性特性的方法可從改進PSD的結構、制作工藝等方面考慮.除此之外,也可以運用數學手段校正其非線性特性,PSD輸出坐標與其理想位置坐標間的關系利用特殊的函數映射來表達.人工神經網絡的迅速發展,為傳感器處理信號提供了有效的手段,可以不提高材料的性能為前提,來提高系統的測試性能.

1 PSD的工作原理

PSD是基于PN結結構的橫向光電效應的器件.如果有N型半導體是輕摻雜的和P+型半導體是重摻雜的組成P+N結結構,當PN結內部載流子的擴散速度與其漂移的速度達到平衡時,建立了一個結電場,其方向由N指向P.當有光照射PN結時,半導體吸收光子獲得能量后激發出電子-空穴對,在結電場的作用下使空穴進入P+區,電子進入N區,從而產生了結電容,就是所說的內光電效應.但是如果入射光僅集中照射在PN結光敏面上的某一點A處，光生電子和空穴也會集中在A點.由于在摻雜濃度方面,P+區遠大于N區,因此進入P+區的空穴由A點迅速擴散到整個P+區,即P+區可以近似地視為等電位.由于N區的電導率較低,進入N區的電子將仍然集中在A點,在PN結的橫向形成不平衡電勢,此不平衡電勢將空穴拉回N區,從而在PN結橫向上建立一個橫向電場,這就是橫向光電效應[3-4].

2 共軛梯度算法分析

2.1 共軛梯度算法的描述

共軛梯度算法(Conjugate Gradient)是介于最速下降法與牛頓法之間的方法,它僅需要利用一階導數信息,就能夠克服最速下降法收斂緩慢的缺點,而且避免了牛頓法要存儲和計算Hesse矩陣求逆的缺點.共軛梯度法不僅可以解決線性方程組,而且是解決非線性最優化問題有效的算法之一.在各種優化算法中,共軛梯度算法是非常重要的一種.其優點是所需存儲量小,具有步收斂性,穩定性高,不需要任何外來參數.

共軛梯度算法是利用目標函數的梯度來逐步產生共軛方向并進行搜索的方法,而無約束問題最優化方法的核心就是選擇搜索方向.非線性規劃問題的一個自變量x沒有任何約束,或說可行域即是整個n維向量空間：x=rn,稱這樣的非線性規劃問題為無約束問題：min{f(x)}.

由泰勒公式可知,一個函數在一個點附近的性態與二次函數是很接近的,由此可知一個算法如果對于二次函數很有效,那么它對于一般函數也會比較好.牛頓法只需要迭代一次就可得到正定二次函數的極小點,而最速下降法一般要求迭代無窮多次才能達到.因此,可以認為牛頓法對于二次函數是有效的.牛頓法每步迭代的計算量很大,經過有限次迭代就可得到正定二次函數極小點的算法是有效的,這種算法被稱為具有二次終止性.共軛方向法是建立在二次模型的基礎上,都具有二次終止性.

2.2 改進的共軛梯度算法

共軛梯度法的基本思想是,如果第k次迭代所取的方向pk與以前各自迭代所取得方向p1,p2,p3…pk-1關于G共軛,則從任意初始點出發,對二次函數進行精確一維搜索,經過n次迭代即可取得極小點.共軛梯度法的優點是不要求精確的直線搜索.但是不精確的直線搜索可能導致迭代出來的向量不再共軛,從而降低方法的效能.克服的方法就是把經過n+1次迭代得到的Xn+1作為初始點重新迭代.改進的共軛梯度算法在此基礎上大大提升了計算的速度.

三層神經網絡由輸入層、隱層和輸出層組成[5],設輸入層的單元數為m,隱層的單元數為l,輸出層的單元數為q,樣本數為p.輸入矢量和希望輸出矢量為x,y,關于網絡權值和閾值的計算可以建立非線性最優化問題來解決[6].即min{f(z)},z∈Rn,該問題的目標函數為

(1)

2.3 改進共軛梯度算法Matlab仿真流程圖

為了更好地研究改進的二維PSD非線性修正共軛梯度算法,利用MATLAB進行了仿真.首先假設一個初始值,設置誤差范圍,沿負梯度方向,根據選擇的初始值,計算出第一個點的梯度,沿負梯度方向和軸的交點為第二個點,判斷第二個點是否符合要求的誤差范圍,如果滿足,則第二個點就是需要的點;如果不符合要求的誤差范圍,第二個點對應曲線上的點沿梯度方向和軸的交點為第三個點,判斷第三個點是否符合要求的誤差范圍,如果滿足,則第三個點就是需要的點,如果不符合,則繼續根據上述方法進行,直到第n個點符合要求的誤差范圍[7-9].

2.4 仿真結果

根據圖1中的Matlab仿真流程圖,在simulink中畫出它的仿真圖,然后運行結果.

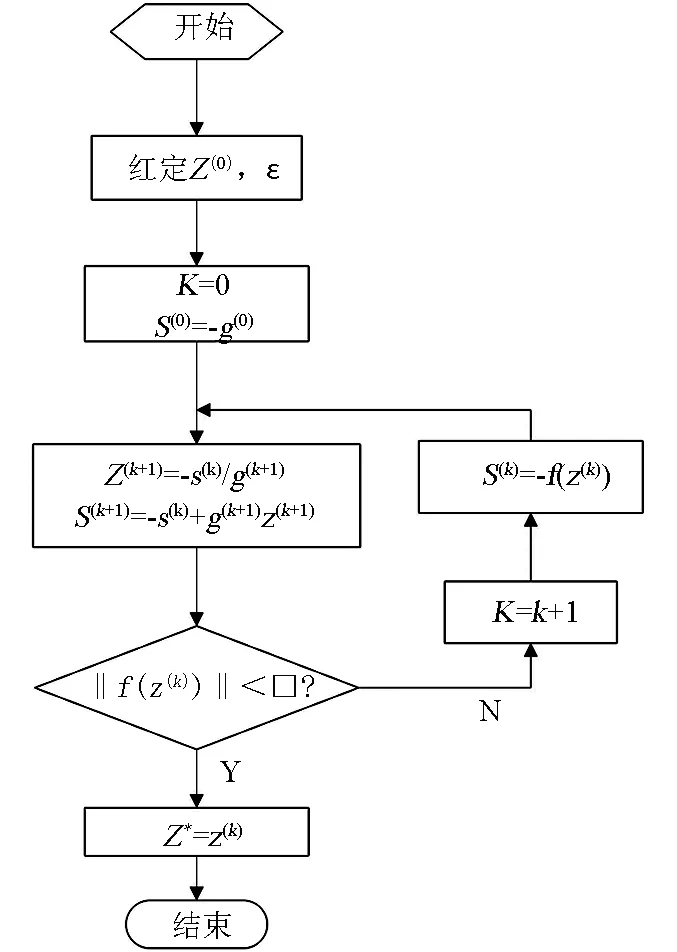
圖1 Matlab仿真流程圖

圖2和圖3提供了改進的共軛梯度算法較共軛梯度算法在提升測量速度方面的優勢的仿真結果.圖2中,當選擇一個初始值,根據共軛梯度算法進行調試,直到一個穩定狀態的過程.t=7s時,共軛梯度算法達到一個穩定狀態.圖3中,當選擇一個初始值,根據改進的二維PSD非線性修正共軛梯度算法進行調試,當t=5s時,達到一個穩定狀態.由此可見,在測量每一組數據時,改進的二維PSD非線性共軛梯度算法可以節省2s,對于需要測量多組數據的實驗,這可以幫助節省很多的時間[10-12].

經過Matlab仿真,改進的二維PSD非線性修正共軛梯度算法是完全可以應用的,并且有絕對的測量速度優勢[13],表1給出了運用改進的二維PSD非線性修正共軛梯度算法的測量值的修正結果.結果與原來的共軛梯度算法相比更加精確.

表1 仿真數據cm

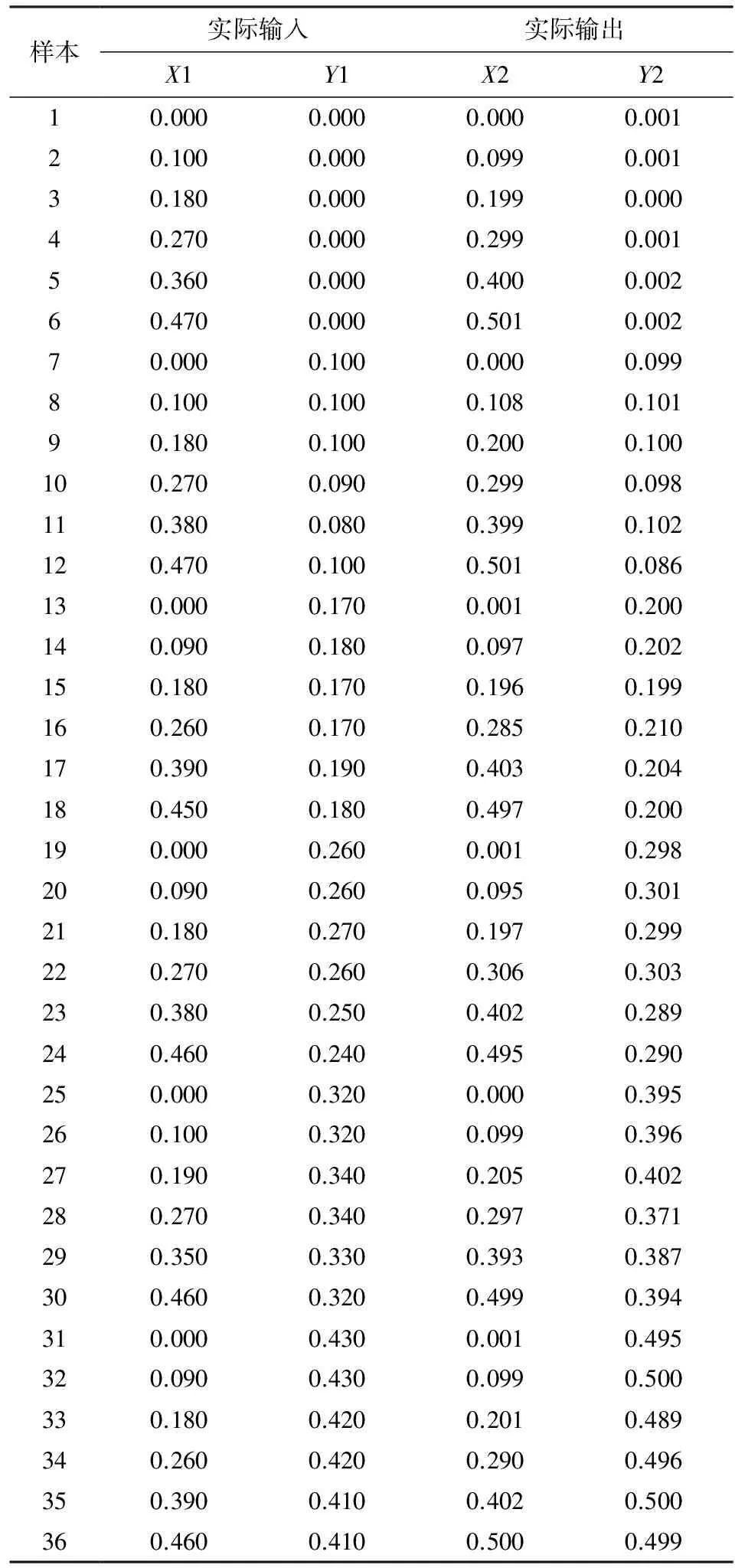
樣本實際輸入實際輸出X1Y1X2Y210．0000．0000．0000．00120．1000．0000．0990．00130．1800．0000．1990．00040．2700．0000．2990．00150．3600．0000．4000．00260．4700．0000．5010．00270．0000．1000．0000．09980．1000．1000．1080．10190．1800．1000．2000．100100．2700．0900．2990．098110．3800．0800．3990．102120．4700．1000．5010．086130．0000．1700．0010．200140．0900．1800．0970．202150．1800．1700．1960．199160．2600．1700．2850．210170．3900．1900．4030．204180．4500．1800．4970．200190．0000．2600．0010．298200．0900．2600．0950．301210．1800．2700．1970．299220．2700．2600．3060．303230．3800．2500．4020．289240．4600．2400．4950．290250．0000．3200．0000．395260．1000．3200．0990．396270．1900．3400．2050．402280．2700．3400．2970．371290．3500．3300．3930．387300．4600．3200．4990．394310．0000．4300．0010．495320．0900．4300．0990．500330．1800．4200．2010．489340．2600．4200．2900．496350．3900．4100．4020．500360．4600．4100．5000．499

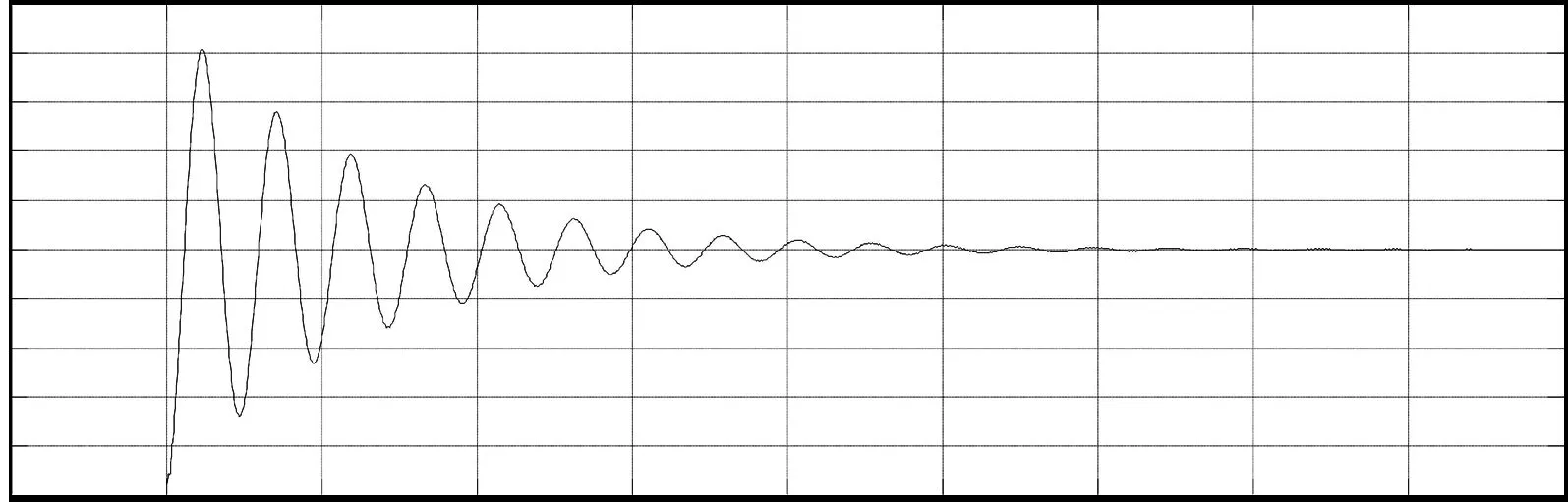
圖2 共軛梯度算法的simulink仿真結果

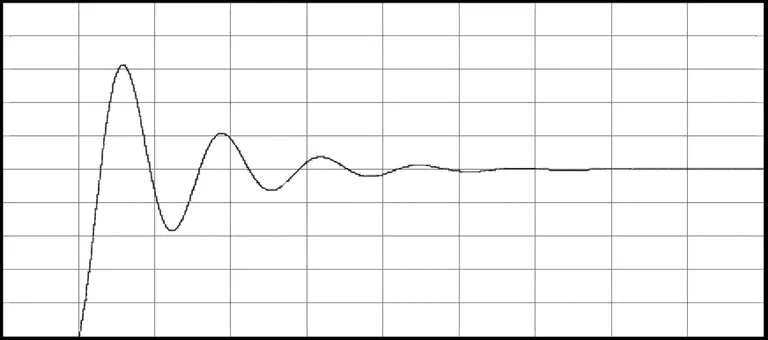
圖3 改進共軛梯度算法simulink仿真結果

除此之外,在精確度不改變的情況下,計算速度大大提升了.表1中,X1、Y1分別表示二維PSD的X方向和Y方向實際輸入,X2、Y2分別表示實際輸出.

3 結束語

改進的神經網絡共軛梯度算法在有效消除PSD非線性特性的同時,在神經網絡的輸出端也可以得到預期的線性輸出,經神經網絡補償后的光電傳感器位置坐標呈線性輸出,從而使PSD的邊緣區域獲得了與中心區域近似的線性度.

改進型共軛梯度算法在不增添設備復雜程度的情況下,提高了邊緣區域的線性度、數據的可信度和計算速度,極大地擴展了PSD在精密測量領域的應用.

[1]周正華,蔣文軍,朱維樂.PSD及其集成裝置標定實驗研究[J].

電子測量與儀器學報, 2000,04(2):6-9.

[2]李博,高藝,王紅平，等.高精度PSD線性化方法與實驗研究[J].長春理工大學學報(自然科學版),2013,36(1):36-39.

[3]李忠科,秦永元,郭強.人工神經網在二維PSD器件非線性修正中的應用[J].計算機測量與控制,2004,12(5)：461-463.

[4]張敏,梁雁冰.二維四邊形位置敏感探測器實驗研究[J].紅外與激光工程,2013,42(2):459-464.

[5]莫長濤,陳長征,張黎麗，等.二維PSD非線性修正共軛梯度算法[J].東北大學學報(自然科學版),2003，24(5):507-509.

[6]SEONGTAEP,CHANGHH.Developmentofpositionsensitiveradiationdetectorsusinggaselectronmultipliers[J].AppliedRadiationandIsotopes, 2009,67(7): 1 476-1 478.

[7]WANGZY,WANGYQ.FuzzynormmethodforevaluatingrandomvibrationofairborneplatformfromlimitedPSDdata[J].ChineseJournalofAeronautics, 2014,27(6): 1 442-1 450.

[8]吳麗雄,黃玉珠.改進二維光電位置傳感器及線性度實驗研究[J].中國測試技術,2006, 32(2):142-144.

[9]王丹,董再勵,孫茂相,等.PSD空間定位的非線性誤差補償模型及歸一化[J].沈陽工業大學學報,2005,27(5):548-552.

[10]李忠科,秦永元.PSD器件自動化標定與非線性修正技術研究[J].激光技術西安,2004, 28(4):370-372.

[11]管炳良,李星,王俊.二維PSD非線性修正技術研究[J].儀器儀表學報,2007,28(7):1 295-1 299.

[12]SATOHS,MUTOS.Developmentoftwo-dimensionalpositionsensitivedetectorsystemsusingmulti-pixelphotoncountersforneutronexperiments[J].NuclearInstrumentsandMethodsinPhysicsResearch2013,731(A): 255-259.

[13]MIRANDAPA,WAHLU,CATARINON,etal.Perfor-manceofresistive-chargepositionsensitivedetectorsforRBS/Channelingapplications[J].NuclearInstrumentsandMethodsinPhysicsResearch2014,760(A):98-106.

(編輯:劉寶江)

Two-dimensional non-linear correction PSD based on improved conjugate gradient algorithm

SHI Chun-yu, LI Tian-ze, TONG Qi-feng, ZHENG Wei

(School of Electric and Electronic Engineering, Shandong University of Technology, Zibo 255049, China)

The causes of the nonlinear characteristics of the two-dimensional PSD and its error are analyzed, adverse effects on the measurement results of nonlinear characteristic of PSD is summarized,and the improved neural network with conjugate gradient algorithm is proposed in this paper. We gradually produce conjugate direction using the gradient of the objective function and use function derivative method for quick search and interpolation. MATLAB simulation results show that this algorithm improves the PSD edge linearity and measurement data accuracy and measuring speed,and extends the application of PSD in the field of precision measurement category without adding the equipment complex.

position sensitive detector;conjugate gradient algorithm;non-liner revision

2016-03-25

山東省自然科學基金項目(ZR2012FL19);山東省高等學校科技計劃項目：(J15LN31)

史春玉, 女,shichunyu910@163.com; 通信作者：李田澤,男,ltzwang@163.com.

1672-6197(2017)02-0027-04

TN

A