馬爾科夫切換隨機區間線性系統的鎮定分析

趙婷婷， 尤蘇蓉

(東華大學 理學院，上海 201620)

馬爾科夫切換隨機區間線性系統的鎮定分析

趙婷婷， 尤蘇蓉

(東華大學 理學院，上海 201620)

研究了具有馬爾科夫切換的隨機區間線性系統的穩定化問題.為得到離散時間反饋控制器，首先設計了連續反饋控制器.通過比較連續時間控制系統和離散時間控制系統的差，得到了離散時間反饋控制器滿足的條件.在此條件基礎上，設計了基于離散時間觀測的反饋控制器.最后給出了一個算例以說明控制方法.

馬爾科夫切換； 區間線性系統； 指數穩定； Lyapunov函數

帶有馬爾科夫切換的隨機微分方程已經被廣泛應用于系統結構和參數會發生突變時的隨機系統建模．關于馬爾科夫切換影響下的隨機系統，文獻[1]建立了其解的存在唯一性及穩定性的完善理論，同時其也是帶有馬爾科夫切換系統領域的第一本專著．在文獻[1]中，諸如Lyapunov函數或者泛函、M -矩陣以及線性矩陣不等式等方法被用于帶有馬爾科夫切換的隨機微分方程或者隨機時滯微分方程的穩定性分析．

在實際應用中，為了得到具體的系統描述，需要估計系統所涉及的參數，如線性隨機系統需要估計其中出現的系數矩陣，由于估計會產生誤差，系統參數帶有多種形式的不確定性，這導致了不確定隨機系統．關于不確定隨機系統的研究，流行的方法有Lyapunov函數法、M矩陣、線性矩陣不等式等．文獻[2-5]先后研究了3種典型的不確定系統：時變結構不確定系統[2-3]、凸多面體不確定系統[4]以及區間系統[5]．文獻[1]的第3章對帶有馬爾科夫切換的區間線性系統的穩定性進行了詳盡的分析．

近年來，隨機系統穩定化問題得到了廣泛的關注，利用不同的控制思想設計了一些有效的控制器與控制方法．文獻[5]利用離散時間反饋控制方法對帶有馬爾科夫切換的隨機系統進行分析，文獻[6]對于不確定線性隨機系統設計了魯棒反饋穩定控制器，文獻[7]設計了不確定隨機系統幾乎必然指數穩定的狀態反饋控制器，文獻[8]考慮了時變時滯和非線性擾動影響下的不確定隨機系統的魯棒隨機穩定化和H問題．

對于不確定隨機系統的穩定化問題，時變結構不確定系統和凸多面體系統得到了較多的關注[2-4]，而對于區間系統的穩定化問題涉及較少．本文將對區間線性系統的穩定化問題進行分析．從控制器的設計上看，傳統的控制器設計方法是基于連續觀測[7-8]，在漂移項或者擴散項上添加控制使得系統均方指數穩定．文獻[5， 9]先后提出了不同的分析方法，研究了基于離散觀測值的狀態反饋控制器的設計方法．本文旨在將基于離散觀測的控制設計方法應用于不穩定的區間線性系統的穩定化分析．

1 符號和穩定化問題

P(r(t+Δ)=j|r(t)=i)=

考慮帶有馬爾科夫切換的線性區間系統

dx(t)= [A0(r(t))+ΔA(r(t))]x(t)dt+

[D0(r(t))+ΔD(r(t))]x(t)dB(t)，t≥0

(1)

定義1 稱線性區間系統(1)為均方指數穩定的，如果存在正數M>0，γ>0，均有E|x(t)|2≤Me-γt．

定義2 若A是一個矩陣，令‖A‖=max{|Ax|:|x|=1}為向量范數．

對于區間系統的指數穩定性判定，文獻[1]提出了一些有效的判斷方法．而對于一個非指數穩定的線性區間系統，期望在漂移項上添加Rn值的狀態反饋控制器u(x(t)，r(t)，t)使得控制系統(2)指數穩定.

(2)

上述控制器的設計基于連續時間狀態反饋，需要對狀態x(t)進行連續觀察．如果僅對于離散時間0，τ， 2τ， ... 進行觀察會更實用、更經濟，其中，τ>0是連續兩次觀測的時間間隔．本文將討論基于系統離散時間觀測值的控制器設計，也就是說控制器u具有的形式為u(x[t/τ]τ，r(t)，t)，這里[t/τ]表示t/τ的整數部分．從而將穩定化問題轉化為在漂移項添加一個離散時間反饋控制器u(x[t/τ]τ，r(t)，t)，使得控制系統(3)指數穩定．

(3)

這里有兩個問題需要解決：一是如何選擇一個適當的τ，二是如何設計控制器u．為了解決上述問題，本文主要分兩部分進行分析：

(i) 討論不穩定輔助系統

ΔDr)y(t)dB(t)

y(0)=x0，r(0)=r0

(4)

的連續反饋控制器的設計，即尋找u(y(t)，r(t)，t)使得控制系統均方指數穩定．

(ii) 選取足夠小的τ，使利用上述連續控制器u產生的離散狀態反饋控制器u(x[t/τ]τ，r(t)，t)可以使控制系統(3)指數穩定．

本文主要任務：尋找并證明使得輔助系統(4)均方指數穩定的控制函數u滿足的條件；尋找τ滿足的條件使得控制系統(3)穩定．

2 主要結論

這里Im是單位矩陣．

假設給定一個不穩定n維線性系統(4)，設計一個線性反饋控制函數

u(x(t)，r(t)，t)=E(r(t))x(t)=

F(r(t))G(r(t))x(t)

添加在漂移項上使得控制的系統

(5)

均方指數穩定．為了方便，記E(i)=Ei，E(i)=F(i)G(i)=FiGi．在實際應用中F和G有一個是已知的，只需要設計另外一個．本文僅給出當G(r(t))已知時，設計F(r(t))的情形，這種設計被稱為狀態反饋控制器．

定理2．1 假設對某個常數γ>0和一系列的Qi∈Rn×nQi=QiT>0，Yi∈Rn×l(i∈S)及正數σ>0使得‖Qi‖≤σ滿足線性矩陣不等式

(6)

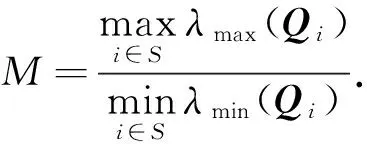
證明：定義函數

V:Rn×S×R+→R+V(y(t)，r(t)，t)=y(t)TQ(r(t))y(t)

顯然滿足

利用引理2．2和2．3可得

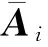
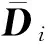
Fi=Qi-1Yi則由條件(6)

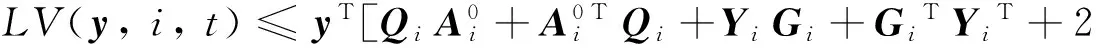
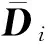
-γV(y(t)，i，t)

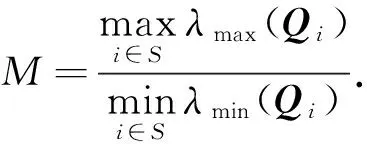
定理2．1給出了基于連續觀測的區間系統穩定化控制器的設計方法．以此線性控制器為基礎，為得到基于離散觀測的控制器設計，即τ的設計，需要比較以下兩系統

之間的差異，分別記兩個系統的解為y(t)與x(t)．關于兩系統的差異,文獻[5]證明了類似結論，歸為引理2．4．

引理2．4 假設存在常數K1，K2，K3對所有的(x，y，i，t)∈Rn×Rn×S×R+滿足

|f(x，i，t)-f(y，i，t)|≤K1|x-y|，

|u(x，i，t)-u(y，i，t)|≤K2|x-y|，

|g(x，i，t)-g(y，i，t)|≤K3|x-y|，

其中

f(0，i，t)=0，u(0，i，t)=0，g(0，i，t)=0，

則兩隨機系統

dx(t)= [f(x(t)，r(t)，t)+u(x([t/τ]τ)，

r(t)，t)]dt+g(x(t)，r(t)，t)dB(t)

dy(t)= [f(y(t)，r(t)，t)+u(y(t)，

r(t)，t)]dt+g(y(t)，r(t)，t)dB(t)

的解

x(t)=x(t；x0，r0， 0)，y(t)=y(t；x0，r0， 0)，

滿足

E|x(t)-y(t)|2≤K(τ)E|x0|2e(2K1+3K2+K32)t，

其中

定理2．2 分別記兩個系統

(7)

(8)

的解為y(t)與x(t)，則E|x(t)-y(t)|2≤K(τ)·E|x0|2e(2a+3b+c2)t．

其中

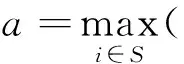
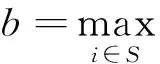
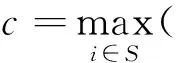
(9)

證明：對于(x，y，i，t)∈Rn×Rn×S×R+令

u(x，i，t)=Erx(t)，

滿足

|f(x，i，t)-f(y，i，t)|≤a|x-y|，

|u(x，i，t)-u(y，i，t)|≤b|x-y|，

|g(x，i，t)-g(y，i，t)|≤c|x-y|．

由引理2．4可知

E|x(t)-y(t)|2≤K(τ)E|x0|2e(2a+3b+c2)t.

定理2．3 假設τ*>0是方程

(10)

的唯一根，其中

(11)

任意固定初始數據x0，r0， 令tk=kτ，xk=x(kτ)，rk=r(kτ)，k=0， 1， 2， ...

x(t)=x(t；xk，rk，tk)， ?t≥tk，

(12)

(13)

由式(13)可得

(14)

以下證明系統(7)和(8)兩解在某一時刻的差異，從而得到某一時刻系統(8)的解所滿足的性質．

E|y(t)|2≤ME|x0|2e-γt，

由式(14)可得

(15)

(16)

而由式(13)可得

e(2a+3b+c2)τ(4M)(2a+3b+c2)/γ

(17)

用式(17)替代式(16)中的相關部分，并利用式(11)則有

(18)

由式(15)和(18)得到

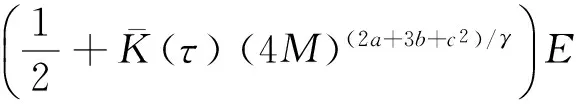
(19)

存在λ>0使得

進而

這證明

(20)

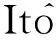
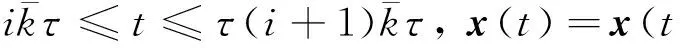
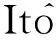
|e+f+g|2≤3|e|2+3|f|2+3|g|2

得到

再利用式(9)得到

由Gronwall不等式得到

再利用式(20)可得

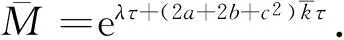
下面給出一個有用的結論，利用定理2．3可以找到如下關于離散觀測控制器的設計方法．

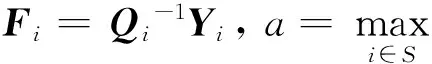
3 算 例

考慮線性不確定系統

(21)

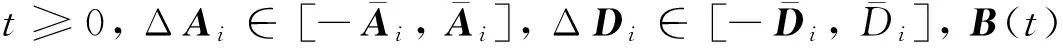
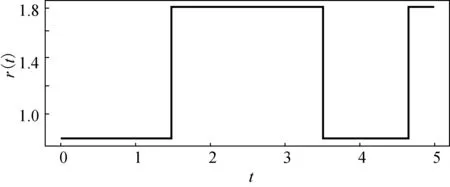
(a) r(t)

(b) x1(t)

(c) x2(t)

這里設計一個離散時間狀態反饋控制器使系統(21)穩定．假設控制系統具有如下形式

(22)

[1]MAOXR，CHENGY．StochasticdifferentialequationswithMarkovianswitching[M]． 2ndEdition．London:ImperialCollegePress， 2006：271-349．

[2]LUCY．AnLMI-basedapproachforrobuststabilizationofuncertainstochasticsystemswithtime-varyingdelays[J]．IEEETransAutomControl， 2003，48(2)：291-296．

[3]WANGC，SHENY．RobustHcontrol for stochastic systems with nonlinearity， uncertain and time-varying delay[J]． Comput Math Appl， 2012，63(5)：985-998．

[4] LI H Y， CHEN B， ZHOU Q， et al． Delay-dependent robust stability for stochastic time-delay systems with polytopic uncertainties[J]． International Journal of Robust and Nonlinear Control， 2008，18(15):1482-1492．

[5] MAO X R． Stabilization of continuous-time hybrid stochastic differential equations by discrete-time feedback control[J]． Automatica， 2013，49(12)：3677-3681．

[6] KHARGONEKAR P P， PETERSEN I R, ZHOU K M． Robust stabilization of uncertain linear systems: Quadratic stabilizability andHcontrol theory[J]． Automatic Control IEEE Transactions on， 1990，35(3):356-361．

[7] UDOM A U． Exponential stabilization of stochastic interval system with time dependent parameters[J]． European Journal of Operational Research， 2012，222(3)：523-528．

[8] XU S Y， LAM J， CHEN T W． RobustH∞control for uncertain discrete stochastic time-delay system[J]． Systems & Control Letters， 2004，51(3/4)：203-215．

[9] MAO X R， LIU W, HU L J． Stabilization of hybrid stochastic differential equations by feedback control on discrete-time state observations[J]． System & Control Letters， 2013，73:88-95．

[10] MAO X R． Stochastic Differential equations and applications[M]． 2nd Edition． UK: Horwood Publishing， 2007：001-190．

[11] 劉金山，吳付科．隨機微分方程導論及應用[M]．6版．北京：科學出版社，2012：17-108．

[12] 龔光魯．隨機微分方程及其應用概要[M]．北京：清華大學出版社，2008：50-98．

(責任編輯：徐惠華)

收稿日期：2015-12-09

作者簡介：陳益松(1964—)，男，湖南寧遠人，教授，博士，研究方向為服裝舒適性及光學三維測量等. E-mail：cys@dhu.edu.cn

文章編號：1671-0444(2017)01-0150-05

Stabilization of Stochastic Interval Linear System with Markovian Switching

ZHAOTingting，YOUSurong

(College of Science， Donghua University， Shanghai 201620， China)

Stabilization of stochastic interval linear system with markovian switching is studied． In order to get a discrete-time feedback controller， firstly， a continuous feedback controller is designed． And then the condition for a discrete-time feedback controller is derived from the difference of continuous and discrete-time feedback controlled system． Based on such condition，the feedback controller based on discrete-time observations can be designed． At last a numerical example is given to vertify our techniques．

Markovain switching； interval linear system； exponential stability； Lyapunov function

2015-11-16

中央高校基本科研業務費專項資金資助項目(16D110906)

趙婷婷(1989—)，女，山東濱州人，碩士研究生，研究方向為隨機微分方程．E-mail：1058216003@qq．com 尤蘇蓉(聯系人)，男，副教授，E-mail：sryou@dhu．edu．cn

1671-0444(2017)01-0144-06

O 211．63

A