基于多尺度融合插值算法的風資源監測方法
蔣何++沈潤杰++陳將威

摘 要 在可持續發展的背景下,風力發電規模迅速增大,風電基地占地面積迅速擴大,導致風資源監測愈發困難。原有的測風塔已很難滿足對大型風電基地中細節風速分布的監測,為風電場運維管理帶來一定困難。本文主要研究一種多尺度風資源立體監測網絡。
【關鍵詞】風資源 多尺度 數據融合 大型風電基地
1 引言
風力是風力發電的基礎,對風電場風資源分布的有效監測是風電場理論出力評估和預測準確性的保障。過往的風電場中簡單利用少量幾個測風塔監測整個風電場的風資源情況,在大型風電基地中會導致風電場群內部大部分區域的風資源情況與實際情況存在一定誤差,對風電場發電分析造成很大的影響。為解決上述問題,本文提出了風電場風資源多尺度立體監測網絡。
為更好地實現對大型風電基地的風資源監測,建立了基于測風塔、風機機頭監測系統及雷達的多尺度立體監測系統。
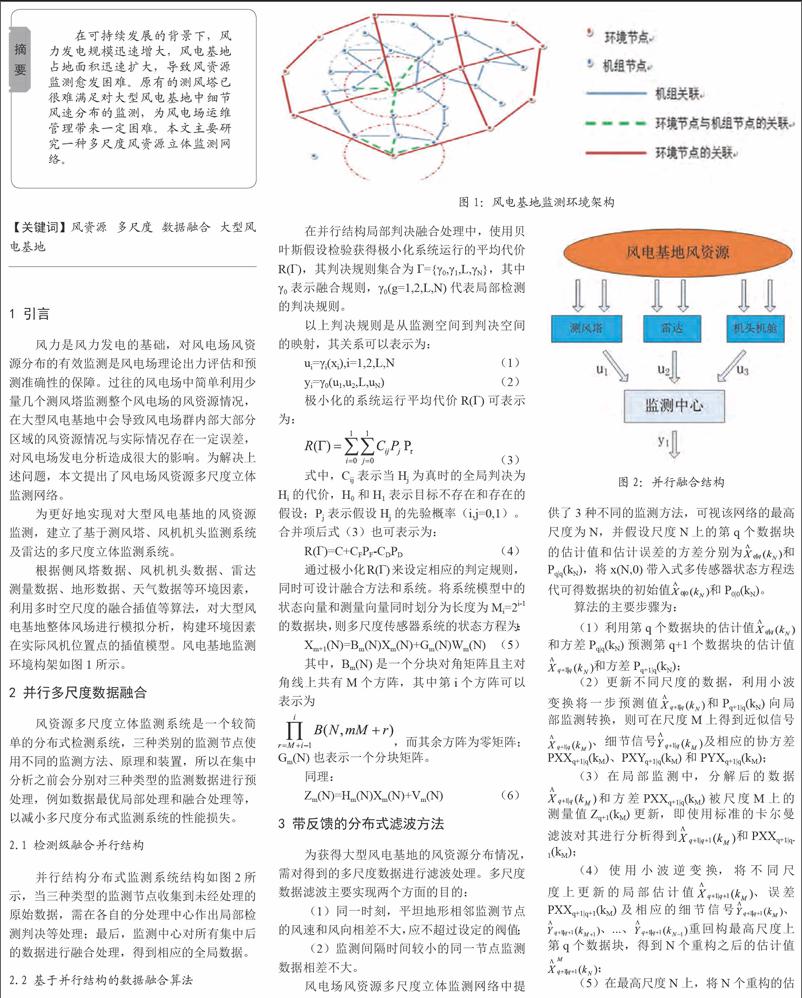
根據側風塔數據、風機機頭數據、雷達測量數據、地形數據、天氣數據等環境因素,利用多時空尺度的融合插值等算法,對大型風電基地整體風場進行模擬分析,構建環境因素在實際風機位置點的插值模型。風電基地監測環境構架如圖1所示。
2 并行多尺度數據融合
風資源多尺度立體監測系統是一個較簡單的分布式檢測系統,三種類別的監測節點使用不同的監測方法、原理和裝置,所以在集中分析之前會分別對三種類型的監測數據進行預處理,例如數據最優局部處理和融合處理等,以減小多尺度分布式監測系統的性能損失。
2.1 檢測級融合并行結構
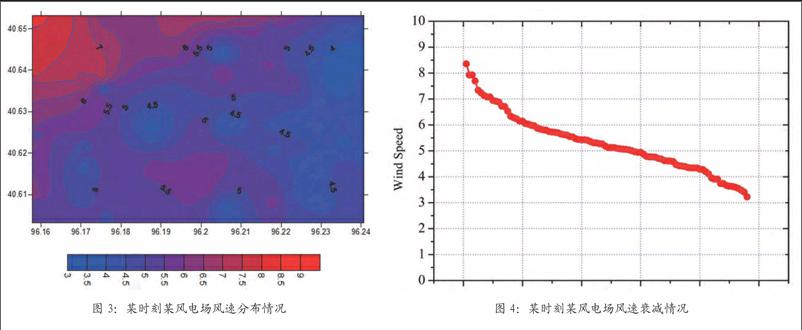
并行結構分布式監測系統結構如圖2所示,當三種類型的監測節點收集到未經處理的原始數據,需在各自的分處理中心作出局部檢測判決等處理;最后,監測中心對所有集中后的數據進行融合處理,得到相應的全局數據。
2.2 基于并行結構的數據融合算法
在并行結構局部判決融合處理中,使用貝葉斯假設檢驗獲得極小化系統運行的平均代價R(Γ),其判決規則集合為Γ={γ0,γ1,L,γN},其中γ0表示融合規則,γ0(g=1,2,L,N)代表局部檢測的判決規則。
新的融合估算值基于以前的融合估算以及新的測量值,小波變換被用來連接不同尺度之間的測量數據。該算法對于多尺度數據濾波融合是很有效的。
4 基于多尺度數據的Kriging插值方法
經多尺度數據融合處理,幾種采集時間間隔不同、范圍不同的數據被融合為相同時間、空間刻度上的數據,并得到插值方法所需要的風資源基礎數據。大型風電基地地形較為復雜,Kriging插值在該類三維空間插值分析中得到了廣泛的應用。
4.1 時空協方差函數
時空域隨機過程滿足二階平穩或固有假設時,其協方差函數可表示為:
式中,U(s,t)表示定義在時空域的隨機過程,且U(s,t)∈Rk×T,其中Rk表示k維的歐氏空間,T代表時間;(s,t)為時空場中任意監測節點的位置,△s為監測節點空間中的距離,△t為時間上的距離。
同時,對應的變差函數可表示為:
實際中多采用簡化的樣本變差函數,如式(10)所示:
4.2 Kriging插值
Kriging方法假定采樣點之間的距離和方向可以反映一些空間相關性,對周圍的測量值進行加權分析得出未測量位置的預測,與反距離權重法類似。Kriging插值是一種線性的無偏估計,并且要求估計誤差的方差最小。在風資源監測環境中,監測節點的空間位置是三維的,所以監測位置參數可表示為si={xi,yi,zi},Kriging插值公式為:
式中,U*(s,t)為待測點(s,t)處的插值;λi為相應監測點的加權系數,當然應滿足∑λi=1,該參數的計算式為:
5 實驗結果
使用上述多尺度插值融合算法,基于某一時刻(2015年1月22日03時10分)雷達監測數據、風機機頭處監測數據和測風塔測量數據,對某一樣本風電場中的風速分布進行分析,整個風電場中的風速的分布情況如圖3所示。從整體上可以看出,風電場上游為強風速區,下游為弱風速區;同時在距離上游一定的距離處,風電場中心的風速明顯小于風電場邊緣兩側的風速,一般風速差能達到1-2m/s。
選取該時刻該風電場的風場數據對整個風電場中風機尾流效應造成的風速衰減現象進行分析。如圖4所示,對該時段整個風電場中所有風機的機頭風速從大到小的排列,結果顯示風速從上游風機機頭風速的8.5 m/s 衰減為下游的3.2 m/s,風速下降率為62.4%。
6 結論
風資源立體監測網絡使用多個尺度的監測數據對大型風電基地風資源進行監測,與過往單一的測風塔監測方法相比更能監測風電基地中風電群場內部細節處的風資源分布情況,使風資源監測的精度大大提高。
參考文獻
[1]胡毅,張建.風資源評估中風速分布方法研究[J].內蒙古科技與經濟,2010(12):76-78.
[2]Yiahak Feliks,Ehud Gavze,Reuven Givati.Optional Vector Interpolation of Wind Fields.Journal of Applied Meteorology,1996,35:1153.
[3]王鵬偉,吳秀清,孫福明.基于多尺度Kalman數據融合濾波[J].光電工程,2008,35(01):110-115.
[4]司長哲,任松.基于Kalman濾波的數據處理多尺度融合算法[J].計算機測量與控制,1999,25(05):627-632.
[5]N.Cressie,G.Johannesson. Fixed rank kriging for very large spatial data sets[J].Journal of the Royal Statistical Society: Series B(Statistical Methodology),2008,70(01):209-226.
[6]周彬彬,蔡建國,馮健.基于ARMA模型和時空Kriging插值聯合模擬大跨結構的脈動風速時程[J].脈動與沖擊,2014,33(03):29-34.
作者簡介
蔣何(1992-),男,四川省人。碩士學位。研究方向為控制科學與工程。
作者單位
同濟大學電子與信息工程學院 上海市 201804

