基于物面弱邊界條件的并行全隱式流場求解方法

高宜勝, 伍貽兆, 夏 健, 徐兆可

(南京航空航天大學 航空宇航學院, 江蘇 南京 210016)

基于物面弱邊界條件的并行全隱式流場求解方法

高宜勝, 伍貽兆*, 夏 健, 徐兆可

(南京航空航天大學 航空宇航學院, 江蘇 南京 210016)

提出了一種基于物面弱邊界條件的Navier-Stokes方程并行全隱式求解方法。首先，實現(xiàn)了非結構網格格點格式有限體積法的粘性物面弱邊界條件。以此為基礎，推導了相應的粘性Jacobian矩陣。相比傳統(tǒng)的物面強邊界條件，弱邊界條件的應用簡化了該推導過程。接著，為了解決Spalart-Allmaras (S-A)模型的收斂和保正性問題，提出了基于物面弱邊界條件的S-A模型無條件保正性收斂方法，通過構造特別的隱式矩陣同時保證S-A模型的收斂和湍流工作變量的正值。流場方程全隱式時間推進和無條件保正性收斂方法所得到的線性方程組采用多色高斯-塞德爾迭代法進行求解，并由MPI實現(xiàn)并行化。通過若干二維和三維算例對本文所提出的方法進行了測試，其結果表明：1) 隨著罰系數(shù)的增大，基于弱邊界條件的結果趨向于基于強邊界條件的結果；2) 對于力的計算，弱邊界條件自動滿足通量一致關系而無需特別處理。

弱邊界條件；Navier-Stokes方程；全隱式方法；保正性方法； 湍流模型

0 引 言

邊界條件處理是CFD計算中極其重要的一個環(huán)節(jié)，直接關系到計算能否收斂、收斂速度快慢等方面。通常，邊界條件的處理可以分為強邊界條件和弱邊界條件。強邊界條件直接給定邊界上的數(shù)值，而弱邊界條件則是通過通量的方式間接引入邊界貢獻。在當前的Navier-Stokes方程數(shù)值計算中，物面邊界為無滑移邊界，一般采用強邊界條件處理，即直接指定物面的速度。強邊界條件概念直觀，實現(xiàn)方便，是目前應用最多的Navier-Stokes方程物面邊界條件處理方式。

近年來，物面弱邊界條件也逐漸得到了研究和應用[1-4]。這是因為相比傳統(tǒng)的強邊界條件，弱邊界條件具有以下優(yōu)勢：(1)在有限差分方法中，弱邊界條件配合分部求和算子(summation-by-parts operators)，能夠實現(xiàn)數(shù)學上可證明的穩(wěn)定格式[5]，而基于強邊界條件尚無相應的結果；(2)Eliasson等人利用非結構網格求解器Edge研究了弱邊界條件和強邊界條件對于定常問題收斂性的影響，發(fā)現(xiàn)弱邊界條件能夠改善收斂性，并提高多重網格的收斂速度[6]；(3)在實現(xiàn)流場全隱式求解或者推導離散伴隨方程的時候，需要推導Jacobian矩陣(或者其轉置形式)，由于強邊界條件下物面點的殘值和流場變量無關，因此Jacobian矩陣(或者其轉置矩陣)需要特別處理[7]；而在弱邊界條件下，可以直接推導相應的Jacobian矩陣，簡化了物面邊界的處理；(4)最近， Stück發(fā)現(xiàn)在強邊界條件下，傳統(tǒng)的力計算公式不滿足通量一致關系(flux consistency)，因此強邊界條件下計算力函數(shù)需要新的計算公式[8]。正因為具有上述優(yōu)點，弱邊界條件正逐步得到應用[9]。而目前國內關于物面弱邊界條件的研究尚屬空白。

本文提出了一種基于物面弱邊界條件的非結構網格并行全隱式流場求解方法。首先，實現(xiàn)了非結構網格格點格式有限體積法的物面弱邊界條件并推導了相應的Jacobian矩陣。與強邊界條件相比，Jacobian矩陣可以直接從黏性通量表達式推導得到而無需特別處理。為了穩(wěn)定求解湍流問題，改進了Shende等人的Spalart-Allmaras(S-A)模型無條件保正性收斂方法(unconditionally positive-convergent implicit scheme， UPC)[10]，提出了弱邊界條件下的UPC方法，保證弱邊界條件下S-A模型的收斂性和湍流工作變量的正值。采用多色高斯-塞德爾迭代法(multicolor Gauss-Seidel iteration，MCGS)求解由流場方程全隱式時間推進和UPC方法所建立的線性方程組，并利用MPI實現(xiàn)并行計算。通過若干算例研究了弱邊界條件的計算結果，并通過與強邊界條件結果的對比，說明了弱邊界條件所具有的優(yōu)點。

1 物面弱邊界條件的實現(xiàn)和Jacobian矩陣推導

1.1 物面弱邊界條件的具體實現(xiàn)

首先采用Eliasson等的方法[6]構造物面弱邊界條件。對于Navier-Stokes方程的絕熱物面邊界，其對流通量的處理和Euler方程滑移物面邊界的處理一致，因此只考慮其黏性通量。物面邊界的黏性通量可以表示為:

(1)

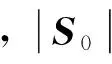
[11]提供了多種計算式(1)中物面速度法向梯度?u/?n的表達式，這里選用其中的第一種，其表示為:

(2)

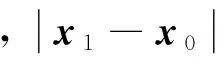
1.2 物面弱邊界條件的Jacobian矩陣推導

為了實現(xiàn)流場全隱式求解，需要推導相應的Jacobian矩陣。在強邊界條件下，由于物面邊界點的速度直接設置為零，物面點的動量方程不起作用，物面點的殘值和流場變量沒有直接聯(lián)系，因此需要采用類似有限元中Dirichlet 邊界條件的處理方式，將全局Jacobian矩陣中物面點的動量方程所對應的行消去，再將對應的對角項設為1，并將對應的右端項設為零。而在弱邊界條件下，物面無滑移邊界條件是利用式(1)計算黏性通量的方式引入的，因此其Jacobian矩陣可以直接通過式(1)的求導得到。這里給出二維情況下的推導，并只考慮對角項即物面點對自身黏性通量的貢獻。

設W為守恒變量，直接推導黏性通量對守恒變量的Jacobian矩陣?G0/?W較為復雜，所以先考慮黏性通量對原始變量的Jacobian矩陣?G0/?Q，其中Q=[ρuvp]T表示原始變量。設?u/?n=[?u/?n?v/?n]T,對式(2)求導，可以得到:

(3)

對式(1)求導，并代入式(3)的結果，有:

式中，nx，ny為n0的分量。根據式(4)可以得到:

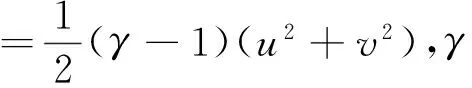
2 基于弱邊界條件的Spalart-Allmaras模型無條件保正性收斂方法

湍流模型的求解是CFD計算中一個較為復雜的問題。因為網格質量不好、數(shù)值離散誤差等原因會造成計算過程中S-A模型的工作變量變?yōu)樨撝担沟糜嬎闶　榱吮苊膺@個問題，可以直接用max函數(shù)進行截斷，但是這樣往往會造成不連續(xù)而影響收斂。針對這個問題，Mor-Yossef等人在兩方程模型上提出了無條件保正性收斂方法(UPC)，通過構造特別的迭代矩陣使得每一步的工作變量都是非負值，并且能夠保證湍流模型計算的收斂[12-13]。隨后，Shende等人又將其發(fā)展到S-A模型上，實現(xiàn)了強邊界條件下S-A模型的穩(wěn)定計算[11]。本文改進了該方法，提出了弱邊界條件下的UPC方法，用于湍流的穩(wěn)定求解。

(6)

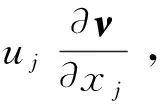
對于每個控制體i，空間離散后的半離散形式S-A模型可以寫為:

式中，Ri表示控制體i的對流項、擴散項和反擴散項綜合起來的殘值，Ωi表示控制體i的體積，Si表示由生成項和消耗項組成的源項。采用一階后向Euler差分離散時間項，則得到全局線性方程組:

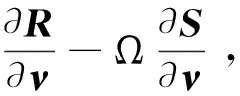
(a)M是M矩陣[15]；

(b) -Rn+ΩSn+Mνn是非負矢量，即每個分量都是非負值。

參考文獻[13]證明了如果矩陣M滿足上述2個條件，則全隱式時間推進

(9)

具有無條件收斂性和保正性，即ν始終為非負矢量。

基于這個結果，需要構造M矩陣并且使其同時滿足條件(b)。參考文獻[15]對于構造M矩陣提供了一個充分條件：如果一個矩陣滿足下面3個要求，則該矩陣為M矩陣：(1)矩陣的所有對角線元素大于零；(2)矩陣的所有非對角線元素非正；(3)對角占優(yōu)，即每行的對角線元素大于該行所有非對角元素的絕對值之和。根據這個充分條件，下面分別考慮式(6)中對流項、擴散項、反擴散項、源項的近似Jacobian矩陣構造。

令Rinv表示對流項的殘值，由于對流項采用一階逆風格式進行離散，那么得到

(10)

(11)

u⊥i,j=ui,jnx+vi,jny+wi,jnz

(12)

(13)

這里，J表示控制體i和控制體j的交界面，SJ表示交界面面積，ui,j，vi,j，wi,j表示控制體i/j的速度分量，nx、ny、nz為單位法向矢量。根據式(10)～(13)，可以得到:

(14)

(15)

即對角線元素大于零，非對角線元素非正，但無法滿足對角占優(yōu)的要求。為了使得對角占優(yōu)，令:

(16)

(17)

則式(14)可以寫為:

(18)

那么

(19)

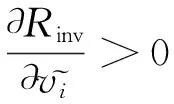
(20)

因此對流項的近似Jacobian矩陣滿足上述的充分條件的要求。

(21)

(22)

(23)

這里，lij表示邊ij的長度，rij表示邊ij的單位邊矢量，nJ控制體界面J的單位法向矢量。因此有:

Rvis=

(24)

(25)式(25)表示擴散項的近似Jacobian矩陣。考慮到整體Jacobian矩陣中還包括對流項和反擴散項的矩陣構造，所以擴散項的矩陣構造只要求對角項大于零而非對角項小于零，而不要求對角占優(yōu)。

對于反擴散項，其離散形式為:

(26)

(27)

采用類似耗散項的處理，有

(28)

考慮到

(29)

令

(30)

這里反耗散項的矩陣構造本身也不滿足M矩陣的充分條件，但是綜合對流項、耗散項和反耗散項的矩陣構造以后仍然滿足M矩陣的充分條件。

接著考慮邊界點對近似Jacobian矩陣的貢獻。對于遠場邊界，由于遠場工作變量梯度較小，所以其耗散項和反耗散項較小，忽略它們的貢獻，只考慮遠場邊界對流項的貢獻。遠場邊界的對流項殘值可表示為

Rfar=F⊥J,farSfar

(31)

(32)

u⊥,far=ufarnx+vfarny+wfarnz

(33)

(34)

這里，ufar，vfar，wfar為遠場邊界的速度，由流場的特征邊界條件得到，Sfar為遠場邊界面積。相應的矩陣構造為:

(35)

對于對稱邊界，由于對稱邊界的法向速度為零，并且工作變量的法向梯度為零，因此沒有通量貢獻，也沒有Jacobian矩陣貢獻。

對于物面邊界，由于物面上工作變量為零，因此沒有對流項和反擴散項的貢獻，只有擴散項的貢獻。弱邊界條件可以按照類似式(2)的方式計算工作變量的法向梯度:

(36)

這里，φ為S-A模型弱邊界條件的罰系數(shù)。那么物面邊界的擴散項對殘值的貢獻為:

(37)

式中，Swall為物面邊界面積。相應的矩陣構造為:

對于源項，將其表示為:

(39)

對應的矩陣構造為:

(40)

這里采用類似參考文獻[14]中源項的處理方法，用max函數(shù)限制源項Jacobian矩陣為非負值。

綜合對流項、擴散項、反擴散項和源項的矩陣構造，得到:

=-Ri+ΩiSi

(41)

式(41)中的近似矩陣構造滿足了UPC的條件(a)，但由于實際求解的是非線性方程組，每個偽時間步迭代中式(41)的右端項都會改變，所以條件(b)不一定能滿足。令

-Ri+ΩiSi

(42)

如果Φ<0，令:

(43)系數(shù)1.5考慮了計算機采用浮點數(shù)表示實數(shù)而帶來數(shù)值精度影響。將式(43)加入式(41)的對角項，得到:

=-Ri+ΩiSi

(44)

需要說明的是，由于UPC方法采用了特別的矩陣構造，為了保證UPC特性，在式(44)的求解過程中必須保證矩陣不發(fā)生改變，所以不能使用LU-SGS這類引入矩陣分解誤差的求解方法。為此，本文采用多色高斯-塞德爾迭代法求解線性方程組，這是因為高斯-塞德爾迭代中矩陣保持不變，因此保證了UPC特性。其具體過程在下節(jié)詳細敘述。

3 多色高斯-塞德爾迭代法

流場的全隱式時間推進和上一節(jié)介紹的UPC方法都需要在每個偽時間步中求解大型稀疏線性方程組。同時考慮到上文所述的UPC求解不能引入矩陣分解誤差的要求，因此采用多色高斯-塞德爾迭代法(MCGS)[17]求解線性方程組，并利用MPI實現(xiàn)了該方法的分布式并行計算。

待求解的線性方程組可以表示為:

Ax=b

(45)

這里，A表示(大型稀疏)矩陣，x為解向量，b為已知右端列向量。傳統(tǒng)的高斯-塞德爾迭代法可以寫為:

(i=1,2,…,n)

(46)

式中，i表示點的編號，對應矩陣的第i行，上標m表示迭代計數(shù)，aii為矩陣第i行的對角項，bi為第i行對應的右端項，Adj(i)表示點i的相鄰點，aij為矩陣第i行的非對角項，n為點數(shù)，即解向量的維數(shù)。為了實現(xiàn)并行求解，首先對網格進行染色。非結構網格點周圍存在數(shù)量不一的相鄰點，需要多種顏色進行染色，來保證每個點和周圍相鄰點的顏色不同，如圖2所示的網格就需要6種顏色進行染色。本文采用最常用的貪心染色算法[18]，其流程如圖3所示。數(shù)值測試顯示，非結構網格染色所需的顏色數(shù)量大致在5～13之間。染色完成后，染成同一種顏色的點相互之間不相鄰，沒有數(shù)據依賴，因此可以按照顏色順序進行并行更新。整個并行MCGS迭代法的計算過程如圖4所示。圖中在Loop3循環(huán)完成以后，采用MPI非阻塞通信更新分區(qū)邊界上相應顏色的ghost點的值，就實現(xiàn)了并行求解。

4 計算結果

4.1 NACA0012翼型的層流流動

首先考慮二維層流流動的結果。計算網格如圖5所示，物面附近采用四邊形單元而其它部分采用三角形單元，網格單元數(shù)為13156，網格點數(shù)為8741。計算狀態(tài)為馬赫數(shù)Ma=0.5，迎角α=1°，Reynolds數(shù)Re=5000。對流通量采用JST (Jameson-Schmidt-Turkel)格式計算[19]。而在黏性通量的計算中，先由Green-Gauss公式得到原始變量的梯度，再采用基于邊修正的方法計算控制體邊界的梯度[20]。前10步CFL數(shù)從10線性增長至10000，然后維持為10000。MCGS迭代次數(shù)為15次。計算平臺為MacBook Pro 15(2013 Later)，編譯器為GFortran 4.9，采用串行方式運行。

圖6給出了弱邊界條件下物面罰系數(shù)σ分別取1、10、100時的翼型表面壓強系數(shù)Cp的分布情況，同時為了與強邊界條件的結果進行對比，還給出了開源CFD代碼SU2[21]在相同狀態(tài)下采用強邊界條件計算的結果(需要說明的是，SU2的對流通量計算同樣采用JST格式，但黏性通量計算方法和邊界條件處理與本文方法不同)。可以看到4條曲線在除了后緣的位置以外幾乎完全重合。圖7給出了后緣部分的放大圖，可以看到隨著罰系數(shù)的增大，弱邊界條件的結果將趨向于強邊界條件的結果。

圖8給出了物面罰系數(shù)σ分別取1、10、100時以及SU2計算的翼型表面摩擦力系數(shù)Cf的分布情況，可以看出4條曲線幾乎完全重合，而圖9給出了后緣部分的放大圖，4條曲線仍然重合得很好。表明采用弱邊界條件可以得到和強邊界條件一致的結果。

圖10顯示了物面罰系數(shù)σ分別取1、10、100時翼型上表面一點以及附近點的速度矢量和速度大小。從圖中可以看出，由于使用了弱邊界條件，壁面點的速度不再為零，但是其數(shù)值大小比其法向點小的多，而且隨著罰系數(shù)的增大將更加趨近于零，因此其對流場計算的影響可以忽略，表明了弱邊界條件可用于黏性流動計算。

圖11給出了物面罰系數(shù)σ分別取1、10、100時密度的收斂歷史，可以看到不同的罰系數(shù)對于收斂影響很小，為了更接近實際的無滑移條件，計算中可以采用較大的罰系數(shù)。

4.2 RAE2822翼型的湍流流動

本算例說明本文方法用于二維湍流計算的情況。計算網格如圖 12所示，物面附近采用四邊形單元捕捉湍流邊界層，而其余部分采用三角形單元，網格單元數(shù)為22842，網格點數(shù)為13937。計算狀態(tài)為馬赫數(shù)Ma=0.729，迎角α=2.31°，Reynolds數(shù)Re=6.5×106。對流通量和黏性通量計算方法同上。流場方程和湍流模型方程的CFL數(shù)在前10步從10線性增長至1000，然后維持為1000。MCGS迭代次數(shù)均為15次。物面罰系數(shù)均取100。計算平臺和上例一樣，同樣采用串行計算。

圖13給出了本文采用弱邊界條件和SU2采用強邊界條件計算的表面壓強系數(shù)以及和實驗數(shù)據[22]的對比。可以看到，本文的計算結果和SU2的結果幾乎重合，與實驗數(shù)據也吻合較好，表明本文基于弱邊界條件的求解體系能夠有效地計算湍流流動，得到與傳統(tǒng)強邊界條件一致的結果。

下面利用該算例來說明不同邊界條件處理對力計算的影響。對于力的計算，可以采用基于物面或者基于遠場的方法，如圖14所示，左圖表示對整個物面積分計算力，右圖表示對整個遠場積分計算力。其標準計算公式可以表示為[8]：

這里dk為單位矢量，對于阻力取來流方向，對于升力取與來流垂直方向，Γ0根據不同的力計算方法表示遠場邊界或者壁面邊界，可見圖14，δkl為克羅內克符號，nl為單位外法向矢量，ΔΓ為表面單元面積。由于流場中沒有額外的力源，理論上基于物面或者基于遠場這兩種方法計算得到的力應該是完全一樣的。但最近Stuck[8]發(fā)現(xiàn)，在強邊界條件下，兩種方法使用式(47)計算出來的力是不一樣的，存在著通量不一致(flux inconsistency)的問題。這是因為強邊界條件直接給定物面點的速度，動量方程不起作用，使得物面處沒有嚴格考慮通量項的貢獻，而在遠場邊界，特征邊界條件是一種弱邊界條件處理，是通過通量的方式引入的，因此遠場處的所有通量項對于力的計算都是有貢獻的，這樣造成了整個計算區(qū)域的通量貢獻不守恒。而采用了弱邊界條件以后，物面邊界條件也是以通量的方式引入的，同時整個流場采用守恒形式有限體積法離散，因此整個流場區(qū)域保持通量守恒，自動滿足了通量一致關系。表1給出了強邊界條件和弱邊界條件下由基于物面和基于遠場方法所得到的升力系數(shù)和阻力系數(shù)的值。可以看到，在強邊界條件下，基于物面和基于遠場的方法計算得到的升力系數(shù)和阻力系數(shù)是不同的，表現(xiàn)出了通量不一致的問題，這與Stuck的結論一致。為了使得強邊界條件下兩種方法計算的力相同，必須采用參考文獻[8]提出的公式而不能使用式(47)。而在弱邊界條件下，基于物面和基于遠場方法計算得到的升力系數(shù)和阻力系數(shù)在機器精度的范圍內一致，自動滿足通量一致關系，無需任何特別處理，表明弱邊界條件相比強邊界條件在計算力的時候更加方便可靠。

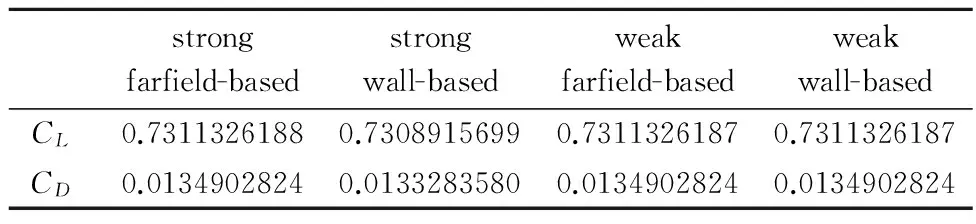
表1 RAE2822翼型湍流流動強邊界條件和弱邊界條件下計算得到的力Table 1 Force functionals obtained by strong and weak imposedboundary conditions for RAE2822 airfoil turbulent flow

4.3 ONERA M6機翼的湍流流動

接下來研究本文方法應用于三維湍流流場求解的情況。計算采用非結構混合網格，如圖15所示，邊界層內采用三棱柱單元，遠場采用四面體單元，過渡部分采用金字塔單元。網格單元數(shù)為915923，網格點數(shù)為2323893。計算狀態(tài)為馬赫數(shù)Ma=0.8395，迎角α=3.06°，Reynolds數(shù)Re=11.72×106。對流通量和黏性通量計算方法同上。流場方程和湍流模型方程的CFL數(shù)在前10步從10線性增長至500，然后維持為500。MCGS迭代次數(shù)均為15次。物面罰系數(shù)均取10000。計算環(huán)境為天津超級計算中心天河1A的2個計算節(jié)點。每個節(jié)點擁有2個Intel Xeon X5670處理器，每個處理器擁有6個核心，主頻為2.93GHz，操作系統(tǒng)為RHEL，編譯器為Intel Fortran 11.1，MPI環(huán)境為天河自主實現(xiàn)的MPI。計算采用24核并行計算。

圖16給出了本文和SU2計算的機翼展向44%和65%這兩個位置的壓強系數(shù)分布以及同實驗數(shù)據[23]的對比。本文的計算結果與SU2的結果非常接近，因此在各展向位置的壓強系數(shù)分布曲線幾乎完全重合，并且和實驗數(shù)據也吻合得很好，說明本文的弱邊界條件適用于三維湍流流動的計算。

表2給出了該算例中采用強邊界條件和弱邊界條件時由基于物面和基于遠場方法所得到的升力系數(shù)和阻力系數(shù)的值。可以看到，和二維情況類似，強邊界條件下同樣出現(xiàn)了通量不一致的問題，而弱邊界條件計算得到的力系數(shù)一致，自動滿足通量一致關系。

表2 ONERA M6機翼湍流流動強邊界條件和弱邊界條件下計算得到的力Table 2 Force functionals obtained by strong and weak imposed boundary conditions for ONERA M6 wing turbulent flow

圖 17對本文方法的并行加速比和理想加速比進行了對比。可以看出當CPU核心數(shù)較少時，并行效率較高，而當CPU核心數(shù)達到24核時并行效率約為77%。因為本文采用的MCGS迭代，在每次循環(huán)一種顏色時都需要通信一次，通信量較大，如果需要進一步改進并行效率，后續(xù)將考慮通信和計算重疊的方法或者采用通信量更小的迭代方法。

5 結 論

本文基于近年來逐步發(fā)展起來的物面弱邊界條件，建立了并行全隱式流場求解方法。在非結構網格格點格式有限體積法中實現(xiàn)了物面弱邊界條件，并推導了相應的Jacobian矩陣。其Jacobian矩陣可以直接由黏性通量表達式推導得到，簡化了流場全隱式計算的推導處理。在此基礎上，提出了弱邊界條件下S-A模型的無條件保正性收斂方法，能夠保證弱邊界條件下S-A模型求解的收斂性和湍流工作變量的正值，實現(xiàn)了湍流流動的穩(wěn)定求解。采用多色高斯-塞德爾迭代法求解全隱式時間推進和S-A模型無條件保正性收斂方法所得到的線性方程組，并利用MPI實現(xiàn)并行計算。對二維、三維條件下的若干層流和湍流問題進行了計算分析，結果表明：(1)隨著物面罰系數(shù)的增大，弱邊界條件下的結果趨向于強邊界條件的結果；(2)對于力的計算，弱邊界條件保證了整個流場的通量守恒，自動滿足通量一致關系，無需特別的處理，因而比傳統(tǒng)的強邊界條件更加方便可靠。

后續(xù)研究工作將深入以下幾個方面：(1)力計算的通量一致問題與對偶一致問題(dual consistency)[24]密切相關，近年來正得到越來越多的重視，對于計算結果的影響需要進一步研究；(2)本文目前的并行效率在CPU數(shù)量增多以后下降較為明顯，需要研究提高并行效率的策略，比如通信和計算重疊的方法，以便用于更大規(guī)模的問題。

參 考 文 獻：

[1]Nordstrom J, Eriksson S, Eliasson P. Weak and strong wall boundary procedures and convergence to steady-state of the Navier-Stokes equations[J]. Journal of Computational Physics, 2012, 231(14):4867-4884.

[2]Bazilevs Y, Michler C, Calo V M, et al. WeakDirichlet boundary conditions for wall-bounded turbulent flows[J]. Computer Methods in Applied Mechanics and Engineering, 2007, 196(49-52):4853-4862.

[3]Bazilevs Y, Hughes T J R. Weak imposition of Dirichlet boundary conditions in fluid mechanics[J]. Computers & Fluids, 2007, 36(1):12-26.

[4]Chandrashekar P. Finite volume discretization of heat equation and compressible Navier-Stokes equations with weak Dirichlet boundary condition on triangular grids[J]. International Journal of Advances in Engineering Sciences and Applied Mathematics, 2016, 8(3):174-193.

[5]Fisher T C, Carpenter M H. High-order entropy stable finite difference schemes for nonlinear conservations laws: Finite domains[J]. Journal of Computational Physics, 2013, 252: 518-557.

[6]Eliasson P, Eriksson S, Nordstrom J. The influence of weak and strong solid wall boundary conditions on the convergence to steady-state of the Navier-Stokes equations. AIAA 2009-3551[R]. Reston: AIAA, 2009.

[7]Giles M B, Duta M C, Muller J D, et al. Algorithm developments for discrete adjoint methods[J]. AIAA Journal, 2003, 41(2):198-205.

[8]Stuck A. Anadjoint view on flux consistency and strong wall boundary conditions to the Navier-Stokes equations[J]. Journal of Computational Physics, 2015, 301: 247-264.

[9]Lakshminarayan V, Sitaraman J, Roget B, et al. Development and validation of a multi-strand solver for complex aerodynamic flows. AIAA 2016-1581[R]. Reston: AIAA, 2016.

[10]Shende N, Mor-Yossef Y. Robust implementation of the Spalart-Allmaras turbulence model for unstructured grid[C]//European Conference on Computational Fluid Dynamics 2010, 2010.

[11]Eliasson P, Nordstrom J. The influence of viscous operator and wall boundary conditions on the accuracy of the Navier-Stokes equations. AIAA 2013-2956[R]. Reston: AIAA, 2013.

[12]Moryossef Y, Levy Y. Unconditionally positive implicit procedure for two-equation turbulence models: Appliciation tok-ωturbulence models[J]. Journal of Computational Physics, 2006, 220(1):88-108.

[13Mor-Yossef Y, Levy Y. The unconditionally positive-convergent implicit time integration scheme for two-equation turbulence models: Revisited[J]. Computers & Fluids, 2007, 38(10):1984-1994.

[14]Spalart P, Allmaras S. A one-equation turbulence model for aerodynamic flows. AIAA 92-0439[R]. Reston: AIAA, 1992.

[15]Berman A, Plemmons R. Nonnegative matrices in the mathematical sciences[M]. New York: Academic Press, 1979.

[16]Svard M, Nordstrom J. Stability of finite volume approximations for the Laplacian operator on quadrilateral and triangular grids[J]. Applied Numerical Mathematics, 2004, 51(1):101-125.

[17]Sato Y, Hino T, Ohashi K. Parallelization of an unstructured Navier-Stokes solver using a multi-color ordering method for OpenMP[J]. Computers & Fluids, 2013, 88(1):496-509.

[18]Saad Y. Iterative methods for sparse linear systems, second edition[M]. Philadelphia: Society for Industrial and Applied Mathematics, 2003.

[19]Jameson A, Schmidt W, Turkel E. Numerical solution of the Euler equations by finite volume methods using Runge-Kutta time-stepping schemes. AIAA 1981-1259[R]. Reston: AIAA, 1981.

[20]Haselbacher A, Blazek J.Accurate and efficient discretization of Navier-Stokes equations on mixed grids[J]. AIAA Journal, 2000, 38(11):2094-2102.

[21]Economon T D, Palacios F, Copeland S R, et al. SU2: an open-source suite for multiphysics simulation and design[J]. AIAA Journal, 2016, 54(3):828-846.

[22]Cook P, Mcdonald M, Firmin M. Aerofoil RAE 2822-pressure distributions, and boundary layer and wake measurements. AGARD Report AR 138[R]. AGARD, 1979.

[23]Schmitt V,Charpin F. Pressure distribution on the ONERA-M6-Wing at transonic Mach numbers. AGARD Report AR 138[R]. AGARD, 1979.

[24]Hicken J E, Zingg D W. Dual consistency and functional accuracy: a finite-difference perspective[J]. Journal of Computational Physics, 2014, 256:161-182.

A parallel full implicit flow solver based on weakly imposed wall boundary condition

Gao Yisheng, Wu Yizhao*, Xia Jian, Xu Zhaoke

(NanjingUniversityofAeronautics&Astronautics,Nanjing210016,China)

A parallel full implicit Navier-Stokes solver based on weakly imposed wall boundary condition is proposed. First, a weak boundary procedure for viscous solid wall is implemented on the unstructured node-centered finite volume method. Upon this procedure, the corresponding viscous Jacobian is derived. Compared to the traditional strongly imposed wall boundary condition, the application of weakly imposed boundary condition eases the derivation. To address the issues of convergence and positivity preserving difficulties with regard to the Spalart-Allmaras (S-A) model, an unconditionally positive-convergent (UPC) implicit scheme for the S-A model using weakly imposed wall boundary condition is presented, which is based on the construction of a special implicit matrix to ensure both the convergence of the S-A model and the positivity of the turbulence working variables. The linear equations resulted from the full implicit time integration and the UPC scheme are solved using multicolor Gauss-Seidel iteration (MCGS) and MPI is employed for parallelization. The proposed approach is tested by simulating several two-dimensional and three-dimensional cases. Results from the numerical simulations demonstrate that: 1) with larger penalty strength parameter, the results of weak boundary conditions tend to those of strong boundary conditions; 2) the weak boundary conditions satisfy flux consistency for force computation automatically, and therefore no special treatment is required.

weakly imposed boundary condition; Navier-Stokes equations; full implicit method; positive scheme; turbulence model

0258-1825(2017)01-0046-11

2016-10-10;

2016-12-04

江蘇高校優(yōu)勢學科建設工程資助項目(PAPD)

高宜勝(1984-)，男，福建福州人，博士研究生，研究方向：計算流體力學. E-mail：gaoyisheng@nuaa.edu.cn

伍貽兆(1945-)，男，江蘇六合人，教授，研究方向：計算流體力學. E-mail：wyzao@nuaa.edu.cn.

高宜勝, 伍貽兆, 夏健, 等. 基于物面弱邊界條件的并行全隱式流場求解方法[J]. 空氣動力學學報, 2017, 35(1): 46-56.

10.7638/kqdlxxb-2016.0121 Gao Y S, Wu Y Z, Xia J. Key technique and aerodynamic configuration characteristic of UCAV with command of the air[J]. Acta Aerodynamica Sinica, 2017, 35(1): 46-56.

V211.3

A doi: 10.7638/kqdlxxb-2016.0121