基于多階段工作轉移矩陣的串行耦合設計任務分配策略
田啟華 梅月媛 劉 勇 杜義賢
1.三峽大學機械與動力學院,宜昌,4430022.三峽大學計算機與信息學院,宜昌,443002
基于多階段工作轉移矩陣的串行耦合設計任務分配策略
田啟華1梅月媛1劉 勇2杜義賢1
1.三峽大學機械與動力學院,宜昌,4430022.三峽大學計算機與信息學院,宜昌,443002
針對串行耦合設計任務的團隊分配因涉及任務的返工而導致分配策略相當復雜這一問題,引入多階段工作轉移矩陣,將任務間的耦合關系以返工量的形式量化,并根據團隊分配衍生矩陣建立串行耦合設計任務分配的數學模型,簡化了串行耦合設計任務的分配過程。利用遺傳算法求解該模型,獲得了不同設計需求下產品開發任務的最佳任務分配方案。以某電動汽車開發項目為例,驗證了該模型的可行性和有效性。
串行耦合設計;多階段工作轉移矩陣;任務分配;設計團隊;遺傳算法
Key works: serial coupling design; multistage work transformation matrix(MWTM); task assignment; design team; genetic algorithm
0 引言
關于設計任務分配的問題,學術界進行了許多研究。如,BASSET[1]采用數學規劃法與啟發式算法,解決了開發團隊的時間與能力最優利用問題;包北方等[2]針對設計任務分配較少考慮任務適合度與任務協調效率的問題,建立了產品定制協同開發任務分配多目標優化模型;武照云[3]針對非耦合集產品開發過程中的任務-團隊分配策略,提出了基于時序邏輯關系的動態分配蟻群優化算法;王志亮[4]提出了名義信息進化度與有效信息進化度的概念,用以解決耦合設計任務的分配問題。以上這些研究中,有的僅針對非耦合集設計任務建立分配數學模型,并不適合解決涉及返工與迭代的復雜產品開發的任務分配問題;有的雖然是針對耦合任務分配問題,但僅以完成時間長短來衡量設計任務分配效果的好壞,評價指標過于單一。
傳統耦合設計任務分配方法大多是利用馬爾可夫鏈(Markov chain)對串行設計任務的執行周期進行建模分析,并通過返工概率描述任務之間的交互關系[4-5]。按照傳統方法思想,設計任務耦合迭代的時間只占整個設計周期的一小部分,總時間的長短更多取決于初始執行周期的大小。因此,為了縮短產品研發時間,只需將任務分配給執行該設計任務花費時間最少的設計團隊即可。此外,對于任務數很多的大容量串行耦合設計任務集,馬爾可夫鏈的應用會隨著任務數的增多而變得更加復雜。
因此,為綜合考慮設計團隊各項指標對設計活動的影響,并簡化計算模型,本文以工作轉移矩陣(work transformation matrix,WTM)來描述耦合設計過程中的反復和迭代,并以該矩陣元素值來定量反映設計任務之間的耦合程度,提出了一種基于多階段WTM的串行耦合設計任務分配策略。
1 基于多階段WTM的串行耦合設計任務分配模型的構建
1.1 任務分配模型相關矩陣的定義
設計任務耦合程度的大小體現了設計任務依賴關系的強弱。依賴關系越強意味著設計任務在執行過程中需要作越多的假設,導致設計任務存在較大程度的返工,依賴越弱則表示設計任務存在較小程度的返工[6-7],因此,設計任務耦合關系可以通過設計任務的返工關系來反映,用WTM來定量描述耦合程度。
WTM作為設計結構矩陣(design structure matrix,DSM)的一種擴展,可以用來分析設計過程中的循環和迭代,并通過耦合任務間的返工定量描述來估計循環迭代過程中的時間和成本[8-9],用W表示。W可以分解成任務返工量矩陣R和任務周期矩陣Z兩個單獨的數值矩陣[10],即W=R+Z。以T1、T2兩個設計任務為例,假設每次任務T1完成后,T2有60%的工作需要重做;而當T2完成之后,T1有30%的工作需要重做;T1獨立完成一次返工工作需要花6個單位時間,而T2獨立完成一次返工工作則需要花5個單位時間。對應的R、Z分別為

其中,Z矩陣中對角元素的取值取決于項目開發前對設計任務的分配。
串行耦合集設計任務的分配問題描述如下:產品開發過程中包含n個任務,任務間存在返工,現在需要分配給m個設計團隊完成。設計團隊作為完成設計任務的主體,其任務完成效果指標是決定任務分配的重要依據。這些指標可通過參考該團隊對之前類似工作的完成情況得到,并用以下矩陣進行描述[4]:
(1)執行周期矩陣Pm×n。當任務在進行分配前,任務周期矩陣Z是不確定的,需依據任務的分配情況從P中取值,矩陣元素pij表示開發團隊i完成任務j時的執行周期。
(2)團隊成本矩陣C1×m。它是一個行矩陣,c1i表示開發團隊i在單位時間內消耗的成本。
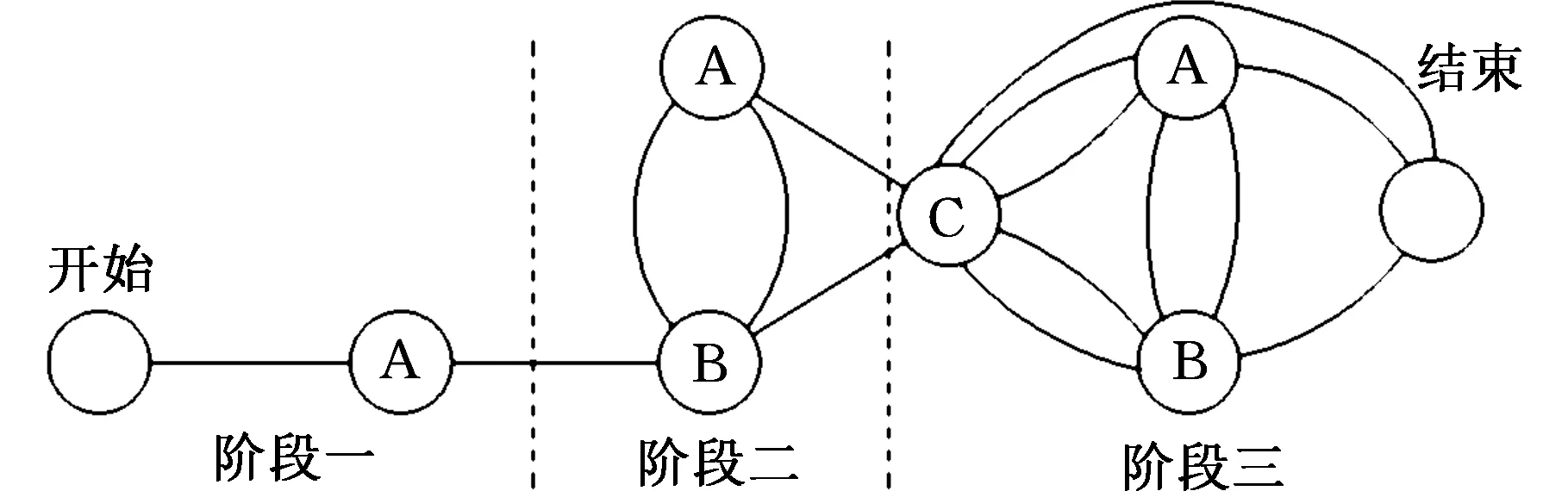
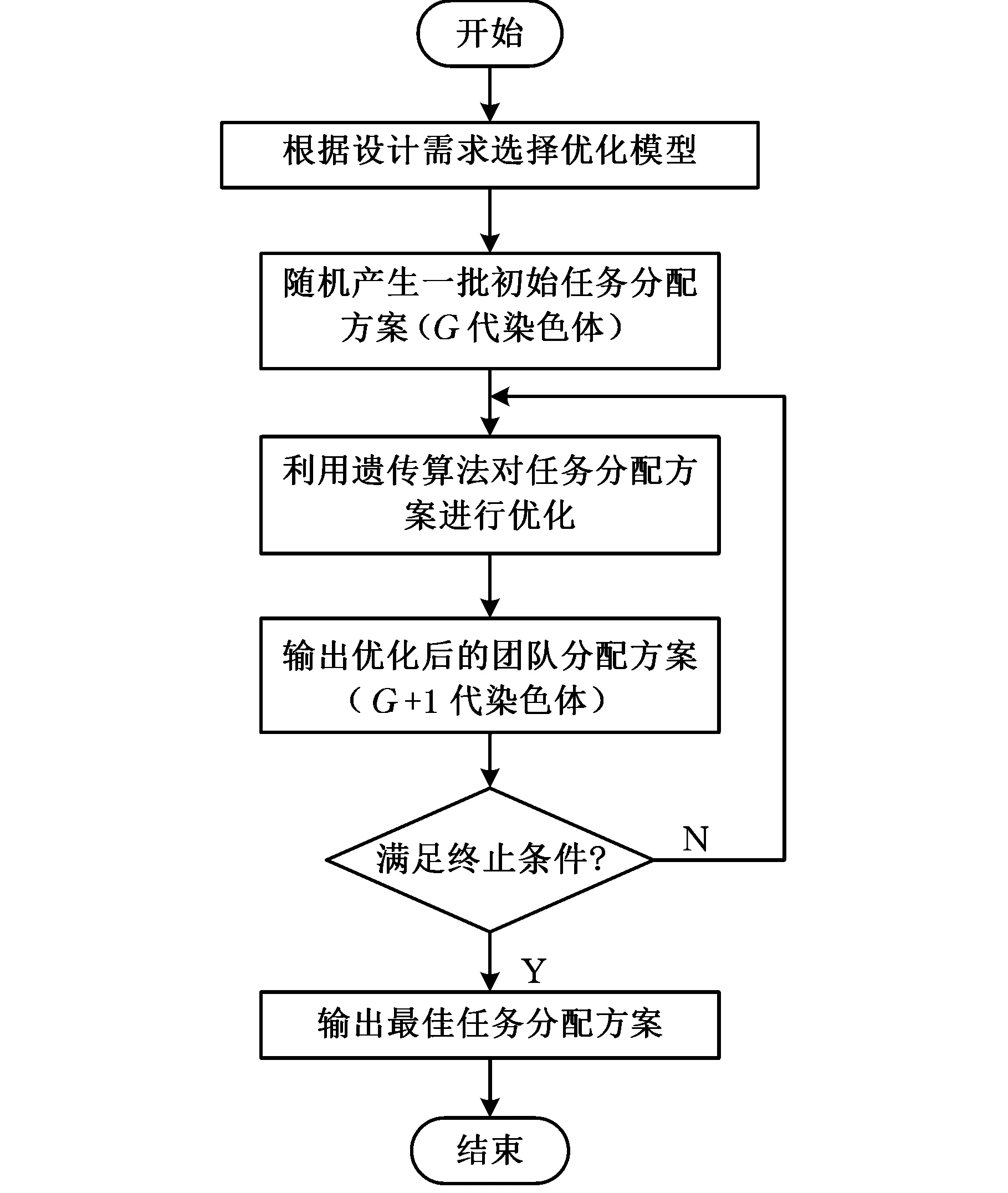
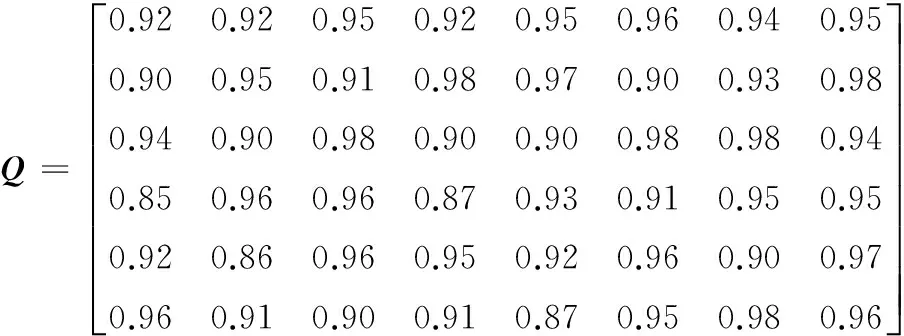
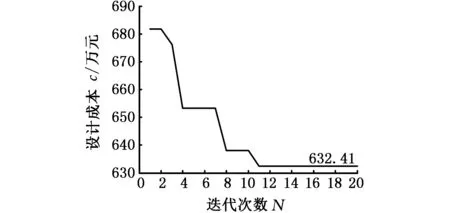
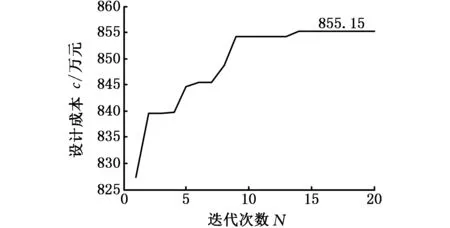
(3)質量指標數矩陣Qm×n。相比時間和成本,質量是一個標量,因此需要進行量化,本文用質量指標數[11]表征設計質量,qij表示開發團隊i完成任務j最終能夠達到的設計質量水平,qij越小,表示質量水平越低;反之,質量水平越高;0 耦合設計任務是單個任務的交互集合,任務本身的性質也會對最終的分配結果造成影響,針對任務的性質引入如下矩陣: (2)初始工作量矩陣Un×1。Un×1是一個列矩陣,ui1表示任務i的初始工作量。 (3)任務分配矩陣Am×n。設計任務分配最終結果是得到設計團隊與任務的對應關系。為了避免團隊之間信息溝通交流額外花費時間,這里規定每個任務只交由一個設計團隊完成,而一個設計團隊可以完成多項任務,可用任務分配矩陣Am×n描述,A是一個[0 1]布爾矩陣,當aij=1時,表示設計團隊i被分配給任務j;aij=0,表示設計團隊i與任務j無關。如有3項設計任務T1、T2、T3交給2個設計團隊m1、m2完成,現將任務T1、T3分配給設計團隊m1,將T2分配給設計團隊m2,則對應的A為 (4)任務分配衍生矩陣Dm×n。Dm×n是A的衍生矩陣,當執行任務j時,將am×n中j≤n列元素保持不變,其他所有元素變為0,即得到Dm×n。上例中,若當前執行任務為T2,則對應的Dm×n為 1.2 任務分配優化模型的構建 WTM模型要求所有的耦合任務并行執行,而在實際中有可能出現其中一些任務由于資源約束或設計要求的改變等原因需要延遲,并在稍后的過程中才能執行。為此,SMITH等[12]進一步提出了多階段WTM設計過程,具體做法是將n個耦合設計任務劃分到r(r≤n)個階段中。在第一個階段中,一個有限任務集的所有任務并行執行;接下來的每個階段所執行的任務均包含兩個部分,即該階段的任務集和前一階段任務集的返工。通過上述描述,當r=n時,每個階段只需執行一個任務,下一個階段的任務包括當前任務和前一個任務的返工。此時任務的執行過程與串行迭代經典模型——馬爾可夫鏈模型(圖1)描述一致。因此,當r=n時,用多階段的WTM設計迭代模型解決串行耦合集設計任務的團隊分配問題是可行的。 圖1 具有3個任務的馬爾可夫鏈模型Fig.1 Markov chain model with three tasks 根據多階段WTM推斷出第一階段任務執行所需時間: T1=‖Z[I-K1RK1]-1K1U‖1 其中,I為n×n維的單位矩陣;K1為第一階段的任務分布矩陣,是一個n×n矩陣,其中的元素定義如下: 第二階段任務執行所需時間: T2=‖Z[I-K2RK2]-1(K2-K1)U‖1 其中,K2為第二階段的任務分布矩陣,其中的元素定義如下: 進而可以推斷出第i階段任務執行所需時間為 Ti=‖Z[I-KiRKi]-1(Ki-Ki-1)U‖1 其中,Ki為第i階段的任務分布矩陣,其中的元素定義如下: 上述各階段Ti表達式中,Z=diag((Pm1,Dm1),(Pm2,Dm2),…,(Pmj,Dmj),…,(Pmn,Dmn)),其中,Pmj、Dmj分別表示Pm×n、Dm×n的第j列元素,(Pmj,Dmj)表示Pm×j與Dm×j的內積。 則各階段所有任務的執行時間T為 (1) 根據D、C以及每個階段的設計時間Ti,可以計算出整個產品開發過程中所需的設計成本: (2) 根據Q、V、A,可以得到最終產品的設計質量指標數Q,用來評價整個產品的設計質量,其中 Q=V× [(Qm1,Am1) (Qm2,Am2) … (3) 式中,(Qmj,Amj)為Qm×n與Am×n第j列元素的內積。 本文涉及的關于時間、成本、質量的優化屬于多目標優化問題,三者均是評價分配方案優劣的重要指標。從實際效果上來講,當然要求時間(T)越短越好,成本(C)越低越好,質量(Q)越高越好。然而,要使多個指標同時達到最優一般是不可能的,比如說成本和質量,想要獲得更高的質量往往意味著投入更多的成本。本文采用多目標優化方法中的ε-目標法[13]對模型進行優化。ε-目標法是選擇眾多優化目標中的一個為主要優化目標,再根據需求對其他優化目標進行評估,得到一個可接受范圍,作為優化模型的約束條件來求解多目標優化問題。依據式(1)~式(3)可以分別建立如下三個優化數學模型。 (1)以時間為優化目標,成本和質量為約束條件建立任務分配數學模型 (4) (2)以成本為優化目標,時間和質量為約束條件建立任務分配數學模型 (5) (3)以質量為優化目標,時間和成本為約束條件建立任務分配數學模型 (6) 式(4)~式(6)中,T、C、Q分別為時間、成本、質量的設計變量,T1、T2、C1、C2、Q1、Q2分別表示根據不同的設計需求確定的設計時間、設計成本、設計質量的范圍。 在建立串行耦合集設計任務分配的數學模型之后,關鍵問題就是如何對這一模型進行有效的求解。對于任務數為n、設計團隊數為m的設計任務分配問題,分配方案共有mn種,隨著m、n的增大,分配方案的數量呈指數級增長。由于復雜產品的設計任務分配過程中n、m的取值一般很大,更加擴大了最佳分配方案的搜索空間,若采用普通啟發式算法進行搜索,結果往往需要等待很長時間。考慮到遺傳算法作為模擬生物環境中遺傳和進化過程而形成的一種自適應全局優化概率搜索算法,無論在搜索空間還是在搜索效率上都有很大改進,并且在一些離散優化問題,如工程調度問題、旅行商問題(TSP)的求解過程中得到了有效的應用[14],因此本文采用遺傳算法解決串行耦合集設計任務的分配問題。具體操作步驟如圖2所示。 圖2 任務分配模型遺傳算法的實現過程Fig.2 Implementation process of task assignment model based on genetic algorithm 首先,根據設計需求選擇相應的優化模型,然后對解決問題的模型準備一批表示起始搜索點的初始任務分配方案G,每個分配方案代表一個編碼的染色體,染色體的長度表示耦合集的任務數,每個編碼位表示設計團隊的編號,利用選擇、交叉、變異3種方式對這個初始群體G進行遺傳操作,實現分配方案的優化,得到新一代群體G+1,接下來遺傳算法會依據適應度函數、任務分配目標與約束條件對新一代種群進行評價,并判斷終止條件[15],若不滿足終止條件,則重復以上過程進行迭代計算,若滿足,則輸出最佳的任務分配方案。 然后,應用MATLAB軟件將建立的3個基于多階段WTM任務分配數學模型(式(4)~式(6))分別轉化成遺傳算法的主程序,并根據串行耦合集設計任務分配的特點,參考旅行商問題(TSP)對應的遺傳算法代碼,編寫初始化、選擇、交叉、變異、適應度評價等對應的MATLAB程序,用以實現最佳分配方案的尋優。 在耦合設計任務中,某些任務的開展需依賴其他任務提供的信息,因此設計項目要按照嚴格的序列執行,即串行執行。電動汽車的開發是典型的串行開發項目。本文以某電動汽車開發項目為例,驗證了基于多階段WTM的串行耦合集設計任務分配模型對獲得最佳團隊分配策略的可行性和有效性。 3.1 問題描述 對該電動汽車的設計開發過程進行分析,可以將該過程簡化為8個設計任務[16],包括:結構大小與動力學特性計算(T1)、馬達規格選擇(T2)、整體重量計算(T3)、存儲能量需求設計(T4)、電池大小與重量設計(T5)、速度與加速度比率設計(T6)、速度與加速度規格設計(T7)和結構與支撐設計(T8),可以將電動汽車的開發過程簡化處理后得到一個8×8的串行耦合設計任務系統,整個項目按照T1—T2—T3—T4—T5—T6—T7—T8的順序執行。 根據對該電動汽車的設計分析,確定任務的返工量矩陣(R)、質量權重矩陣(V)如下: V=[0.15 0.10 0.10 0.15 0.15 0.10 0.15 0.10] 矩陣R中元素值量化了該電動汽車設計過程中各個設計任務之間耦合關系的強弱。其中,元素值為非0表示任務之間存在耦合關系,其值越大表明設計任務之間耦合關系越強;元素值為0則表示設計任務之間沒有耦合關系。 根據實際情況,將上述8個設計任務分配給6個設計團隊(m1、m2、m3、m4、m5、m6)。每個團隊對每個任務的完成效果不同,表示設計團隊各項指標的矩陣P、C、U、Q如下: C=[252225212324] 3.2 問題求解 按照本文串行耦合設計任務的分配思想:執行周期長短、設計成本高低和設計質量好壞等因素均可以描述電動汽車開發任務分配方案的好壞,因此需要綜合考慮。限于篇幅,本文選取設計成本為評價指標進行說明。此時的任務分配問題可以描述為:怎樣將任務分配給設計團隊才能滿足設計時間和設計質量的要求,同時使整個設計項目的總成本最低。根據以往完成類似工作的經驗,任務分配后完成時間必須在20~35天內,設計質量指標數要達到0.95以上,即將設計時間限定在[20,35]區間內,設計質量指標限定在[0.95,1)區間內。按照優化目標和約束條件,選取式(5)模型按照圖2所示的流程進行求解,將設計任務個數8設置為染色體的長度,設計團隊編碼用1~6的正整數表示,適應度函數取個體的設計成本。選擇算子選用的是隨機遍歷抽樣運算,交叉運算使用單點交叉算子,變異運算使用均勻變異的算法,根據任務分配方案可行解的大小將種群的數量設置為200,終止代數、交叉概率、變異概率分別設置為20、0.7、0.06[15]。 運行式(5)模型對應的MATLAB遺傳算法程序,得到最優個體函數值曲線如圖3所示。圖4表示滿足相同設計需求下最差個體函數值曲線。 圖3 各代最優個體設計成本Fig.3 The best individual design costs of generations 最優個體對應的團隊分配矩陣A為 圖4 各代最差個體設計成本Fig.4 The worst individual design costs of generations 3.3 結果分析 對本文建立的模型進行求解,從圖3可以看出,隨著迭代次數的增加,項目的開發成本逐漸降低,最優個體出現在第12代,之后的代數成本保持不變,說明采用遺傳算法尋優是有效的。從所得到的矩陣A可以看出最后得到的任務分配方案為:任務T1、T6分配給團隊m5,任務T2、T3和T8分配給設計團隊m4,任務T4、T5、T7分別分配給團隊m1、m2、m3,而團隊m6將不參與此次設計任務,對應的設計成本為632.41萬元。而從圖4中可以得到相同設計需求下設計成本的最大值為855.15萬元。比較兩種方案對應的效果,最小設計成本相比于最大設計成本減小了34.7%。本文通過分別選擇式(4)、式(6)模型對項目的設計時間和設計質量進行方案尋優,也得到類似的結論。 本文通過引入多階段WTM建立任務分配模型,并通過構建任務分配衍生矩陣,得到了串行耦合集設計任務分配的有效數學模型。該方法不僅簡化了串行耦合集設計任務的分配計算過程,還考慮了設計團隊的多項指標對串行耦合設計任務分配效果的影響。實例應用分析結果表明該任務分配策略是可行且有效的。在實際產品開發中,項目管理者應用該方法,可以對串行耦合產品設計的最終完成效果進行預先分析,因而提高了對產品開發結果的可預見性,為進行設計任務分配提供了更為科學的理論依據。 [1] BASSET T. Assigning Projects to Optimize the Utilization of Employees Time and Expertise[J]. Computers Chemical Engineering, 2000,24:1013-1021. [2] 包北方, 楊育, 李雷霆,等. 產品定制協同開發任務分配多目標優化[J].計算機集成制造系統, 2014, 20(4):739-746. BAO Beifang, YANG Yu, Li Leiting, et al. Multi-objective Optimization for Task Allocation of Product Customization Collaborative Development[J]. Computer Integrated Manufacturing Systems,2014,20(4):739-746. [3] 武照云. 復雜產品開發過程規劃理論與方法研究[D].合肥:合肥工業大學,2009. WU Zhaoyun. Research on Theory and Method of Complex Product Development Process Planning[D]. Hefei: Hefei University of Technology, 2009. [4] 王志亮. 復雜產品敏捷化開發中若干關鍵決策技術的研究[D].南京:南京理工大學,2004. WANG Zhiliang. Research on Decision-making Techniques for Agile Development of Complex Product[D]. Nanjing: Nanjing University of Science Technology, 2009. [5] 汪鳴琦,劉傳勝.工程迭代設計的過程管理研究[J]. 武漢科技大學學報,2011,34(3):210-214. WANG Mingqi , Liu Chuansheng. Process Management in Engineering Iteration Design[J]. Journal of Wuhan University of Science and Technology ,2011,34(3):210-214. [6] 汪鳴琦,陳榮秋,崔南方. 工程迭代設計中產品族開發過程的研究與建模[J]. 計算機集成制造系統, 2007,13(12):2373-2381. WANG Mingqi, CHEN Rongqiu, CUI Nanfang. Modeling of Product Family Development Process in Engineering Iteration Design[J]. Computer Integrated Manufacturing Systems, 2007,13(12):2373-2381. [7] 王志亮,張友良. 復雜耦合系統設計過程動態規劃[J]. 計算機工程與應用,2005(13):117-120. WANG Zhiliang, ZHANG Youliang. A Dynamic Decision Model for the Complex Coupled System’s Design Process[J].Computer Engineering and Applications,2005(13):117-120. [8] SMITH R P, STEVEN D. Eppinger Identifying Controlling Features of Engineering Design Iteration[J]. Management Science: Journal of the Institute of Management Sciences, 1997,43(3): 276-293. [9] 陳希,王寧生.虛擬企業環境下的復雜產品并行開發框架模型研究[J].控制與決策,2003,18(6):716-719. CHEN Xi, WANG Ningsheng. Study on the Framework of Complex Product Concurrent Development in a Virtual Enterprise[J]. Control and Decision , 2003,18(6):716-719. [10] 陳庭貴. 基于設計結構矩陣的產品開發過程優化研究[D].武漢:華中科技大學,2009. CHEN Tinggui. An Optimization Approach to Product Development Process Based on Design Structure Matrix[D]. Wuhan: Huazhong University of Science and Technology,2009. [11] 杜微,莫蓉,李山,等. 基于產品關鍵特性的質量鏈管理模型研究[J]. 中國機械工程,2013,24(11):1516-1520. DU Wei, MO Rong, LI Shan, et al. Quality Chain Management Model Based on Product Key Characteristics[J]. China Mechanical Engineering, 2013,24(11):1516-1520. [12] SMITH R P, EPPINGER S D. Deciding between Sequential and Concurrent Tasks in Engineering Design[J].Concurrent Engineering Research and Applications,1998,3:15-25. [13] 張瑞軍,邱繼偉,王曉偉,等.基于多目標非耦合優化策略的可靠性穩健優化設計[J].中國機械工程,2014,25(2):246-250. ZHANG Ruijun, QIU Jiwei, WANG Xiaowei,et al. Reliability-based Robust Optimization Design Based on Strategy of Multi-objective Optimization Uncoupling or Decoupling[J]. China Mechanical Engineering, 2014,25(2):246-250. [14] 董寧. 求解約束優化和多目標優化問題的進化算法研究[D].西安:西安電子科技大學,2015. DONG Ning. Study on Evolutionary Algorithms for Constrained Optimization and Multiobjective Optimization Problems[D]. Xi’an: Xi’an University of Electronic Science and Technology,2015. [15] 史峰,王輝,郁磊,等. MATLAB智能算法30個案例分析[M].北京: 北京航空航天大學出版社, 2011:45-46. SHI Feng, WANG Hui, YU Lei, et al. Thirty Case Analysis about Intelligent Algorithm in MATLAB[M]. Beijing: Beihang University Press, 2011:45-46. [16] 曾小華, 宮維鈞. ADVISOR 2002電動汽車仿真與再開發應用[M].北京: 機械工業出版社, 2014:62-63. ZENG Xiaohua, GONG Weijun. ADVISOR 2002 Electric Vehicle Simulation and Application Development[M]. Beijing: China Machine Press, 2014:62-63. (編輯 王艷麗) Task Assignment Strategy for Serial Coupling Product Design Based on MWTM TIAN Qihua1MEI Yueyuan1LIU Yong2DU Yixian1 1.College of Mechanical and Power Engineering, China Three Gorges University, Yichang,Hubei,443002 2.College of Computer and Information Technology, China Three Gorges University, Yichang,Hubei,443002 The task assignment strategy for serial coupling product design, which involved the rework of tasks, was very complex. To solve the problem, the MWTM was introduced to quantify the coupling relations among the tasks in rework amounts. Based on the task assignment derivative matrix, a model of the task assignment for serial coupling product design was built. This model was solved by genetic algorithm and so the optimal task assignment strategy of product design might be obtained for different design requirements. Taking the development of an electric car as an example, validity and feasibility of this model were proved. 2016-04-27 國家自然科學基金資助項目(51475265) TH122;TP391 10.3969/j.issn.1004-132X.2017.05.013 田啟華,男,1962年生。三峽大學機械與動力學院教授、博士。主要研究方向為機械設計及理論、CAD/CAM/CAE等。發表論文70余篇。梅月媛,女,1991年生。三峽大學機械與動力工程學院碩士研究生。劉 勇,男,1975年生。三峽大學計算機與信息學院教授、博士。杜義賢,男,1978年生。三峽大學機械與動力學院副教授、博士。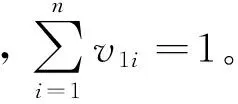
(Qmj,Amj) … (Qmn,Amn)]T2 基于遺傳算法的任務分配模型的求解
3 應用分析



4 結語

