基于遺傳算法的伺服系統PID控制參數整定

姚 禹， 王 博， 高 智*

(1.長春工業大學 應用技術學院， 吉林 長春 130012;2.長春市軌道交通集團有限公司, 吉林 長春 130012)

0 引 言

串并聯數控機床伺服系統具有多變量、非線性、強耦合的特點[1-4]，為了滿足不同的加工需求，串并聯數控機床要求多個控制模塊共同協作，故此對應用在其上的控制器要求較高。PID控制器具有原理簡單、易于應用、魯棒性強的優點，在以往數控機床中應用的非常廣泛[5-7]。然而，由于串并聯數控機床伺服系統控制器要調節電流環、速度環和位置環的多個變量，同時這些變量又存在著并不十分明顯的耦合關系，使得串并聯數控機床伺服系統極易受負載擾動的影響，若采用常規PID控制，控制器的參數選擇則異常困難[8-10]，這使得串并聯數控機床的伺服系統難以取得滿意的控制效果。

針對這一問題，文中利用遺傳算法整定串并聯數控機床伺服系統的PID控制參數解決耦合對PID控制參數的影響。通過種群的多樣性和較強的尋優能力[11-12]，快速尋優電流環和速度環PID控制參數，實現對串并聯數控機床伺服系統PID控制參數的整定，提高伺服系統的控制精度和適應性。通過仿真分析，驗證了所提方法具有調節時間短、無超調、魯棒性強等優點，可改善串并聯數控機床伺服系統的控制性能，進而提高串并聯數控機床的加工精度。

1 遺傳算法的基本原理

基本的遺傳算法以包含解集的種群為對象，個體之間依據某種規律進行交叉、變異操作。交叉操作即是兩個不同的個體的參數進行交換，而變異操作即是個體上的某一參數按照某一概率發生變化。而后，在生成的新種群中具有優越性能的個體存活下來，適應性差的個體被拋棄。如此循環，達到進化的目的[13-14]，直到性能最優越的個體或滿足某一要求的個體出現，進化結束。

文中定義的遺傳算法里，每一個個體看成一個特定參數的集合，代表著控制器電流環、速度環和位置環的10個控制參數，個體間經過交叉和變異產生子代個體，然后再把這些個體和子代個體放在一起競爭產生新的2代個體，2代個體重復上述過程產生3代、4代、5代個體等，直到找到一個性能最優越的個體或產生的所有個體都收斂于某一區間，進化過程結束，產生的個體代表PID控制參數調節適當，可將該PID控制參數在串并聯數控機床伺服控制器內進行設置。

2 基于遺傳算法的PID控制參數整定

2.1 個體的設計與初始化

個體是遺傳算法進化過程的基礎，個體設計的好壞直接影響遺傳算法對串并聯數控機床伺服系統PID控制參數的搜索能力和搜索速度。在設計串并聯數控機床伺服系統PID控制參數個體時要考慮個體的大小、初始化和多樣性等，以確保串并聯數控機床伺服系統PID控制參數個體收斂，進而保證遺傳算法的收斂性。串并聯數控機床伺服系統PID控制參數個體意義見表1。

表1 串并聯數控機床伺服系統PID控制參數個體意義

2.2 適應度函數的設計

表征伺服系統適應度函數的指標有很多，如超調量、上升時間、調節時間、穩態誤差等。即便對于相同的控制系統，只要控制目標不一致，其適應度函數也可以是不一致的。適應度函數可以根據某一性能指標建立，也可以根據多個性能指標，如取各性能指標的加權平均，以系統誤差最小為優化目標建立，或以工藝要求建立。但需保證群體中各個個體在優化計算中可能達到或接近達到最優解。

文中根據串并聯數控機床伺服系統具有的非線性、強耦合的特點，為了獲取滿意的過渡過程，在串并聯數控機床伺服系統PID控制參數整定過程中，將適應度函數取為目標函數的倒數。這樣在利用遺傳算法對串并聯數控機床伺服系統的電流環、速度環和位置環的PID控制參數進行尋優時，適應度函數值最大的那一組個體參數即為最優的串并聯數控機床伺服系統PID控制參數。故此，將誤差絕對值、時間積分性能作為最小目標函數，并且為了防止控制過度，加入了其控制輸入的平方項。具體串并聯數控機床伺服系統PID控制參數整定的最優指標為:

(1)

而后，根據串并聯數控機床的加工特點，為了保證加工工件的精度，要求串并聯數控機床伺服系統沒有超調量。為滿足這一要求，在對串并聯數控機床伺服系統的PID控制參數進行尋優時，引進了懲罰機制，只要一出現超調量，就立即把超調量作為一目標值，如果：

ey(t)<0

則

(2)

2.3 編碼

對串并聯數控機床伺服系統中電流環、速度環和位置環的10個PID控制參數進行尋優，每個個體代表了在遺傳算法中參數尋優問題時的一個可能解。設樣本個數為N，比例系數Kp、積分時間常數Ti、微分時間常數Td變化范圍為[a,b]，b>a>0，則比例系數為：

(3)

式中:r----Kp的二進制碼。

同理，積分時間常數Ti、微分時間常數Td也做類似的處理。

2.4 遺傳算子的選擇

在對串并聯數控機床伺服系統PID控制參數進行尋優時，需要對群體中的個體進行優勝劣汰的競爭操作即選擇，它是在評價適應度函數的基礎上建立的。對種群中的個體而言，適應性越高的個體，在競爭中越具有優勢，它遺傳到下一代中的可能性就會越大；相反，適應性越低的個體，它遺傳到下一代中的可能性就會越來越小。

文中在串并聯數控機床伺服系統PID控制參數尋優過程中，選用的是賭盤法對遺傳算子進行選擇，如圖1所示。

圖1 賭盤法示意圖

2.5 遺傳算子的交叉

遺傳算法中種群產生子代個體的主要途徑就是交叉，它是從選中的個體中選擇父親和母親的基因參數產生新的子代個體。對于每兩個基因參數，這種選擇機會是平等的。例如在對串并聯數控機床伺服系統PID控制參數尋優時，每個個體包含電流環、速度環和位置環的10個PID控制參數，選擇一個個體后，隨即產生一個二進制數組：1010110010，數字1代表該基因參數是從母親個體處遺傳，數字0代表該基因參數是從父親個體處遺傳。正是這樣不統一的交叉，直至進化的結束，才保證了種群的優越性可以遺傳給子代個體。

2.6 遺傳算子的變異

遺傳算法中種群產生子代個體的另一個途徑就是變異，但變異是雙向的。它既可以產生種群中沒有過的優良基因參數，也可以破壞種群中原本就有的優良基因參數。為了保證種群的優越性和多樣性，在串并聯數控機床伺服系統PID控制參數尋優過程中，需要交叉和變異相互配合，這樣可以增強遺傳算法的隨機搜索能力，共同完成對空間的全局和局部搜索，找到最合適的串并聯數控機床伺服系統PID控制參數。

3 基于遺傳算法的PID控制參數尋優步驟

針對上文所述的串并聯數控機床伺服系統PID控制參數進行尋優，找到性能優越、滿足串并聯數控機床伺服系統控制精度要求的PID控制參數,利用的遺傳算法流程如圖2所示。

圖2 遺傳算法流程

4 仿真研究

為了驗證所提算法的有效性，基于Matlab仿真環境建立了串并聯數控機床雙閉環調速系統，如圖3所示。

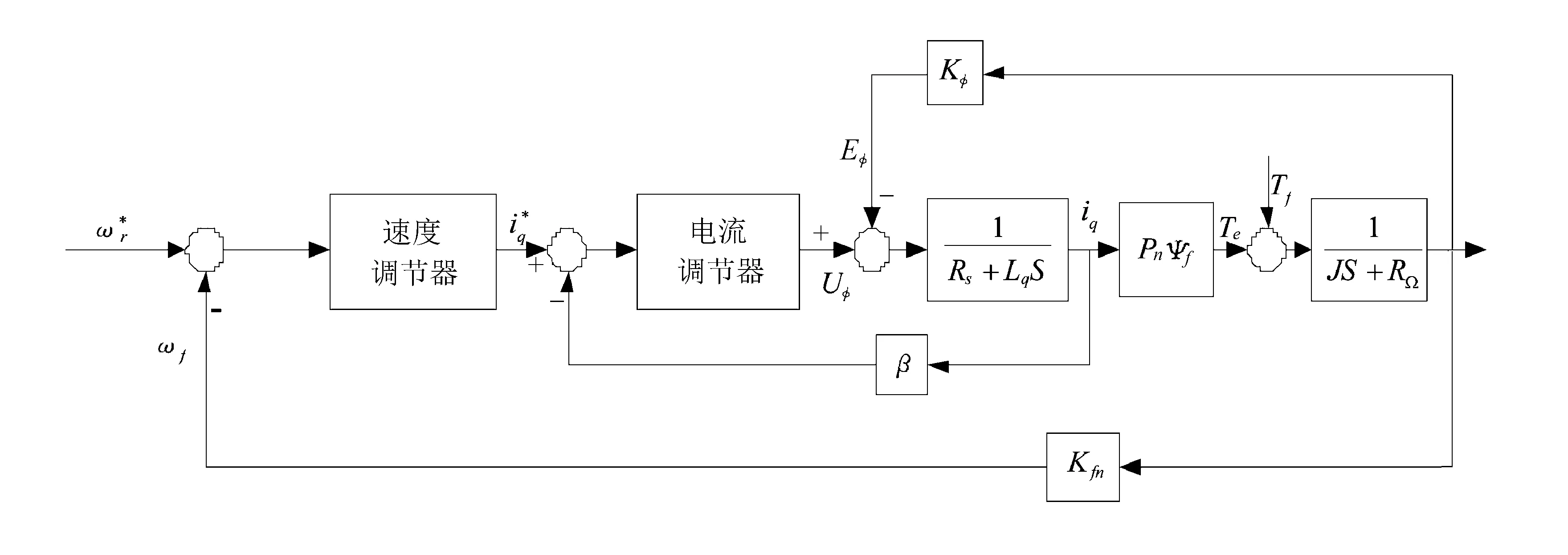
圖3 串并聯數控機床伺服系統雙閉環控制結構圖

電流環調節器的傳遞函數為：

(4)

速度環調節器的傳遞函數為：

(5)

利用遺傳算法對PID控制參數進行尋優，經過100代的優化過程后得到了電流環PID的控制參數結果為:Kp=17.9，Ki=0.93，Kd=0.03；速度環PID的控制參數結果為:Kp=11.42，Ki=0.40，Kd=0.05。

電流環的目標函數曲線和PID控制參數尋優曲線如圖4所示。

(a) 電流環目標函數曲線 (b) 電流環PID控制參數尋優曲線

圖4 電流環控制性能曲線

給出了速度環的目標函數曲線和PID控制參數尋優曲線，并給出了當輸入為階躍響應曲線時，應用遺傳算法尋優后的系統響應曲線,如圖5所示。

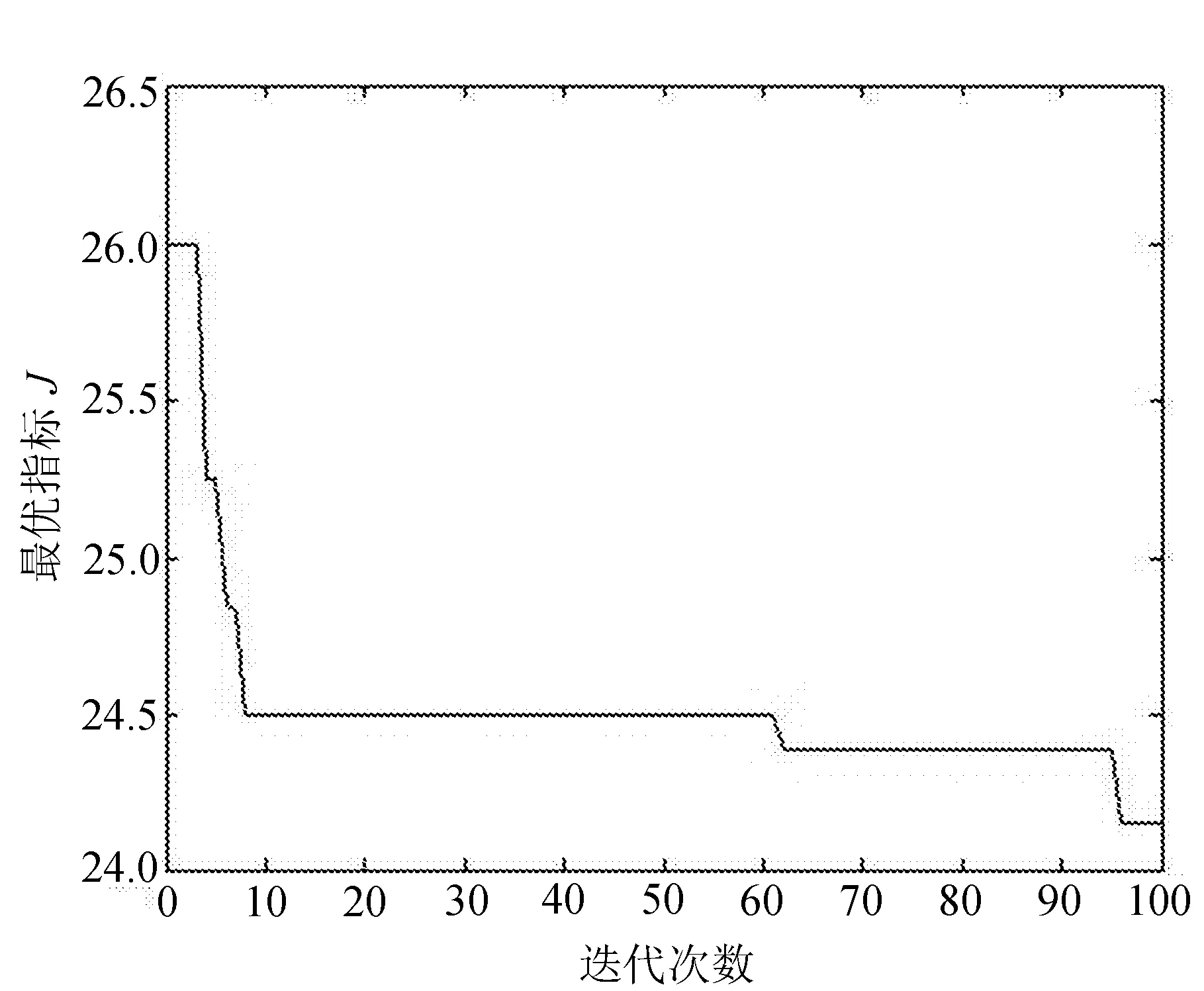
(a) 速度環目標函數曲線 (b) 速度環PID控制參數尋優曲線

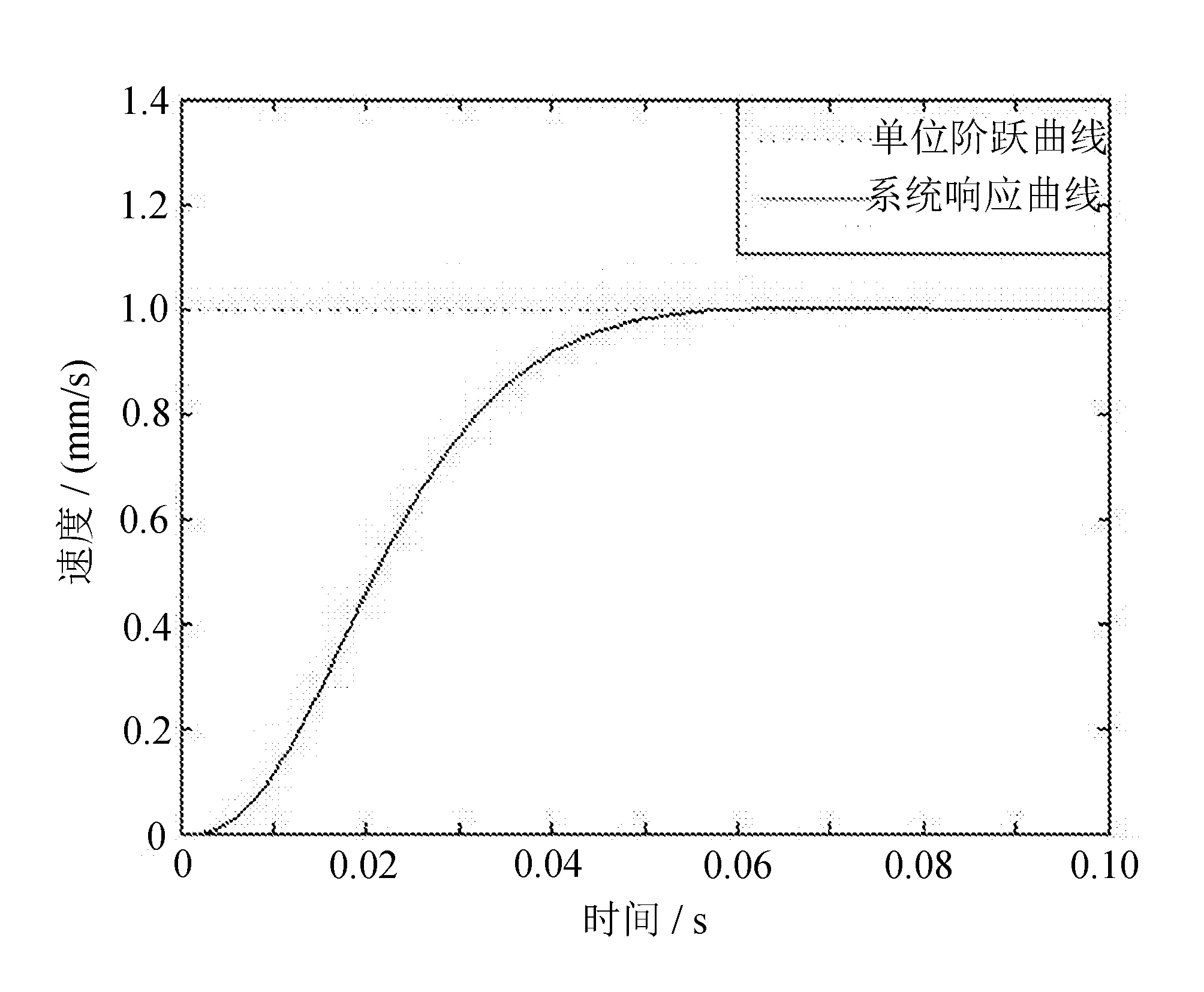
(c) 速度環階躍響應性能曲線

通過圖4和圖5的仿真結果分析，文中利用遺傳算法對串并聯數控機床伺服系統PID控制參數尋優，由于引入了抵制超調量的懲罰因子(見式(2))，可以使圖4和圖5中的目標函數較小，參數尋優較快，且對串并聯數控機床伺服系統控制性能進行階躍響應仿真時，超調量均為σ%=0(見圖5(c))，表明文中提出的基于遺傳算法的PID控制參數整定方法可以使串并聯數控機床伺服系統的響應時間變短，無超調量，可提高串并聯數控機床伺服系統的控制精度，進而改善串并聯數控機床的加工性能。

5 結 語

針對串并聯數控機床伺服系統具有多變量、非線性、強耦合的特點，提出基于遺傳算法的串并聯數控機床伺服系統PID控制方法，利用遺傳算法快速尋優PID控制參數，實現對PID控制參數的整定。遺傳算法可同時完成優化電流環、速度環和位置環控制器的10個控制參數，避免了采用傳統方法多次優化才能完成對多個控制器參數整定的繁瑣。仿真結果表明，算法響應速度快，無超調，消除了穩態誤差，使串并聯數控機床伺服系統能獲得滿意的過渡過程和性能指標，進而提高了串并聯數控機床的加工精度。

[1] 蔡赟,張邦成,姚禹.3PTT-2R串并聯數控機床動力學耦合特性研究[J].農業機械學報,2015(12):362-369.

[2] 張邦成,王占禮,王義強，等.3-PTT串并聯數控機床伺服系統運動學耦合特性研究[J].農業機械學報,2013(11):316-321.

[3] 張邦成,王義強,蔡赟，等.3-PTT串并聯數控機床構型設計與位姿分析[J].農業機械學報,2011(9):207-212.

[4] 姚禹,張邦成,蔡赟，等.改進的強跟蹤濾波算法及其在3PTT-2R伺服系統中的應用[J].自動化學報,2014(7):1481-1492.

[5] 譚顯坤,宿靖波,李雷.PID控制器的模糊優化與參數學習自整定(英文)[J].機床與液壓,2013,24:116-120.

[6] 金林駿,方建安,潘磊寧. 一種基于改進的粒子群優化算法的神經網絡PID控制器[J].機電工程,2015(2):295-300.

[7] 柴光遠,趙鵬兵.模糊自適應PID控制器在液壓AGC系統中的應用[J].機床與液壓,2010(6):69-71,27.

[8] 黃銀萍,唐志勇.工程機械電液比例閥控制系統模糊PID控制器研究[J].機床與液壓,2010(13):52-54,18.

[9] Jian SUN, Feng LIU, Jennie SI, et al. Direct heuristic dynamic programming based on an improved PID neural network[J]. Journal of Control Theory and Applications,2012,10(4):497-503.

[10] 周頔.基于遺傳算法和模糊神經網絡的PID控制器參數優化方法[J].計算機與現代化,2013(9):8-12.

[11] 郝齊,關立文,王立平.基于遺傳算法并聯機床電機伺服系統控制參數整定[J].清華大學學報:自然科學版,2010,11:1801-1806.

[12] 吳玫,陸金桂.遺傳算法的研究進展綜述[J].機床與液壓,2008(3):176-179,172.

[13] 馬永杰,云文霞.遺傳算法研究進展[J].計算機應用研究,2012(4):1201-1206,1210.

[14] 張裊娜,李昊林.模糊RBF神經網絡PID在汽車定速巡航控制系統應用[J].長春工業大學學報,2017，38(3):237-244.