基于復(fù)合模型動(dòng)力蓄電池SOC估算

高順榮， 謝慕君

(長春工業(yè)大學(xué) 電氣與電子工程學(xué)院， 吉林 長春 130012)

0 引 言

蓄電池是電動(dòng)汽車的心臟，需要對(duì)它管理和研究。在實(shí)際生活中用的很普遍的就是磷酸鐵鋰電池，因?yàn)樗泻芏嗥渌姵夭痪邆涞膬?yōu)勢(shì)。荷電狀態(tài)(SOC)是蓄電池的一個(gè)重要指標(biāo)，為了提升蓄電池的使用功效，有必要得到確切的SOC估測(cè)值。實(shí)際情況中對(duì)電池的使用有很多種要求，這就促使人們用許多不同的方式來獲得確切的SOC，如安時(shí)計(jì)量法[1]、開路電壓法[2]、卡爾曼濾波法[3]等；文中針對(duì)安時(shí)計(jì)量法不能估算電池初始狀態(tài)及存在積累誤差的問題，應(yīng)用安時(shí)計(jì)量法、開路電壓法及擴(kuò)展卡爾曼濾波法相結(jié)合對(duì)電池SOC進(jìn)行估計(jì)。通過安時(shí)計(jì)量法表達(dá)式離散化獲得電池狀態(tài)方程，引入電流系數(shù)及溫度系數(shù)，獲得電池的復(fù)合模型，再采用EKF估算磷酸鐵鋰電池的SOC。

1 基本原理

1.1 蓄電池SOC的概念

SOC定義為蓄電池目前剩余電量與在同樣的放電前提下100%的電池能放出總?cè)萘康谋戎?

(1)

式中:Cd----剩余電量；

Ci----電池能放出的總?cè)萘浚?/p>

CR----電池放出的電量。

1.2 安時(shí)計(jì)量法

安時(shí)計(jì)量法來計(jì)算SOC，不需要考慮磷酸鐵鋰電池里面的化學(xué)反應(yīng)和結(jié)構(gòu)變化，只需通過對(duì)電流的積分就能知道SOC。安時(shí)計(jì)量法表示如下：

(2)

式中:SOC(t)----電池在t時(shí)的SOC；

SOC(t0)----電池在t0時(shí)的SOC；

C0----電池的額定容量；

i----t時(shí)的電流；

η----i對(duì)應(yīng)的充放電效率。

安時(shí)計(jì)量法在現(xiàn)實(shí)使用中存在一些問題：

1)SOC(t0)不容易獲得，假如SOC(t0)計(jì)算不精確的話，最后計(jì)算出的值也會(huì)有些偏差；

2)由于電池的容量特征，電流i和溫度T都會(huì)影響到電池的實(shí)際釋放容量。

因此，為了獲得確切的SOC，就要解決這兩方面的問題。

1.3 開路電壓法

電池停止工作以后，里面的電化學(xué)反應(yīng)也會(huì)穩(wěn)定下來，它的電壓會(huì)逐漸達(dá)到一個(gè)恒定值，其中這個(gè)不變的電壓就是電池的等效電動(dòng)勢(shì)(E)，再根據(jù)E-SOC關(guān)系就能知道SOC(t0)的值。

1.4 卡爾曼濾波法

KF能確切地估計(jì)SOC，在SOC的估算中，把電流和溫度作為輸入量，電池的端電壓作為輸出量，SOC作為狀態(tài)變量[4]。磷酸鐵鋰電池是非線性系統(tǒng)，因此，采用EKF來估測(cè)SOC，EKF所使用的系統(tǒng)狀態(tài)空間模型為[5]：

狀態(tài)方程：

xj+1=h(xj,uj)+ωj

(3)

觀測(cè)方程：

yj=g(xj,uj)+υj

(4)

式中：h(xj,uj)、g(xj,uj)----分別為狀態(tài)轉(zhuǎn)移函數(shù)和觀測(cè)函數(shù)；

ωj----系統(tǒng)的狀態(tài)噪聲；

υj----系統(tǒng)的測(cè)量噪聲。

2 復(fù)合模型的建立

在安時(shí)計(jì)量法中，為了考慮放電電流的大小和溫度對(duì)電池實(shí)際釋放容量的影響[6]，引入等效電流系數(shù)和溫度系數(shù)，表達(dá)式如下：

(5)

2.1 等效電流系數(shù)ηi

因?yàn)殡姵厝萘刻卣鲗?duì)SOC估測(cè)的干擾，把等效電流系數(shù)代入安時(shí)計(jì)量法中；1897年P(guān)eukert總結(jié)出一個(gè)公式，也稱為Peukert方程，它主要是關(guān)于蓄電池恒流放電電流和持續(xù)時(shí)間的關(guān)系[7]。

int=Const

(6)

式中：i----放電電流；

t----充滿的電池持續(xù)放電到截至電壓的時(shí)間；

n----與電池類型有關(guān)的常數(shù)，取n=0.989 25[8]；

Const----和電池活性物質(zhì)有關(guān)的固定值。

Ci=it表示電流為i時(shí)的可用容量，將它代入式(6)，得：

Ci=Const×i1-n

(7)

(8)

(9)

聯(lián)合式(8)和式(9)可以解得：

(10)

再結(jié)合式(7)可求得等效電流系數(shù)ηi：

(11)

2.2 溫度系數(shù)ηT

環(huán)境溫度對(duì)電池容量也有干擾，一般來講，隨著周圍溫度的上升，電池釋放的容量會(huì)有所增加，現(xiàn)在經(jīng)常采用經(jīng)驗(yàn)公式來描述溫度與容量的關(guān)系[9]。

CT=C20[1+mT(T-20)]

(12)

式中:CT----T時(shí)的容量；

C20----20 ℃時(shí)刻的容量；

mT----常數(shù)，通常為0.006～0.008。

設(shè)

ηT=[1+mT(T-20)]-1

則有

若以20 ℃為標(biāo)準(zhǔn)，則C20就是額定容量C0。

2.3 模型建立

使用EKF估測(cè)電池SOC時(shí)，需要采用電池模型。把修正后的安時(shí)計(jì)量法式(5)用泰勒級(jí)數(shù)展開[10]，得：

(13)

其中，SOC是狀態(tài)變量xj,得到了復(fù)合模型的狀態(tài)方程：

(14)

復(fù)合模型的觀測(cè)方程是由三種簡單的電化學(xué)模型組合得到。

Shepherd模型:

(15)

Unnewehr universal模型:

yg=E0-Rig-Kixg

(16)

Nernst模型：

yg=E0-Rig+K2lnxg+K3ln(1-xg)

(17)

將Shepherd模型、Unnewehr universal模型和Nernst模型的模型函數(shù)多項(xiàng)式進(jìn)行相加，統(tǒng)一模型參數(shù)，得復(fù)合模型的觀測(cè)方程：

K3lnxj+K4ln(1-xj)

(18)

式中:ij----j時(shí)刻的電流；

yj----端電壓；

R----固定阻值；

K0----磷酸鐵鋰的開路電壓；

K1、K2、K3、K4----磷酸鐵鋰的模型參數(shù)，依據(jù)實(shí)驗(yàn)數(shù)據(jù)，再通過最小方差法計(jì)算獲得涉及到的參數(shù)值。

3 估測(cè)電池SOC

根據(jù)上述過程創(chuàng)立模型，設(shè)計(jì)復(fù)合模型的卡爾曼濾波算法獲得SOC[11]。

3.1 模型的選擇

考慮環(huán)境溫度T和電流i因素以后，得到修正后的電池復(fù)合模型的狀態(tài)方程和觀測(cè)方程如下：

xj+1=h(xj,uj)+ωj=

(19)

yj=g(xj,uj)+υj=

K3lnxj+K4ln(1-xj)+υj

(20)

3.2 系統(tǒng)動(dòng)態(tài)特性匹配系數(shù)的確定

把電池模型的狀態(tài)方程和觀測(cè)方程用Taylor級(jí)數(shù)展開，并利用Jacobin矩陣求解得到模型匹配系數(shù)。狀態(tài)方程里面的系數(shù)值為：

(21)

(22)

觀測(cè)方程的動(dòng)態(tài)匹配系數(shù)為：

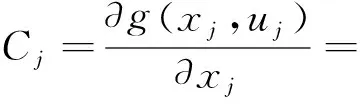
(23)

(24)

另外，系統(tǒng)輸入的求解表達(dá)式為：

uj=ij

(25)

通過上述推導(dǎo)可知狀態(tài)方程：

xj+1=Ajxj+Bjuj+ωj

(26)

觀測(cè)方程為：

yj=Cjxj+Djuj+υj

(27)

在具體過程中用Dω表示過程噪聲誤差，Dυ是觀測(cè)噪聲誤差，EKF執(zhí)行過程如圖1所示。

圖1 EKF的流程圖

4 方法驗(yàn)證與分析

為了檢驗(yàn)基于復(fù)合模型的EKF,可以很好地計(jì)算磷酸鐵鋰電池組的SOC,用實(shí)驗(yàn)室的磷酸鐵鋰電池組測(cè)量電池的SOC，歷時(shí)600 s，采樣間隔3 s，得到SOC的變化值。間隔30 s的部分實(shí)驗(yàn)數(shù)據(jù)見表1。

表1 部分實(shí)驗(yàn)數(shù)據(jù)

針對(duì)觀測(cè)方程式(18)中的參數(shù)，令參數(shù)向量

ρ=[K0,R,K1,K2,K3,K4]T

矩陣

E=[e1,e2,…,eN]

矩陣E的列向量

定義向量

Y=[y1,y2,…,yN]

模型觀測(cè)方程可等效為

Y=Eρ

因此，利用已知的Y和E就可以求出參數(shù)向量ρ，即

ρ=(ETE)-1ETY

其中，磷酸鐵鋰電池組的模型參數(shù)計(jì)算值[12]見表2。

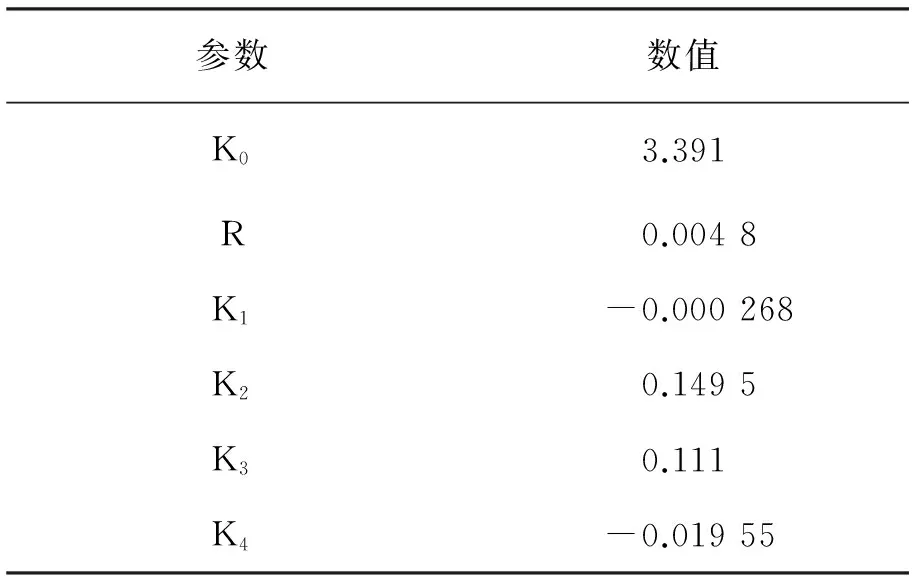
表2 模型參數(shù)

在SOC理論算法推導(dǎo)的基礎(chǔ)上，采用Matlab進(jìn)行仿真實(shí)驗(yàn)，檢驗(yàn)基于復(fù)合模型的EKF能很好地計(jì)算磷酸鐵鋰電池組的SOC。從仿真實(shí)驗(yàn)看出，采用EKF估算出復(fù)合模型的SOC值，根據(jù)時(shí)間的變化可以很快地逼近測(cè)量值，如圖2所示。

圖2 SOC計(jì)算值與實(shí)驗(yàn)值的對(duì)比

將復(fù)合模型計(jì)算的SOC仿真結(jié)果與實(shí)驗(yàn)室的測(cè)量值進(jìn)行對(duì)比，誤差剛開始還有點(diǎn)明顯，但減小的非常迅速，這在一定程度上也表明,基于復(fù)合模型的卡爾曼濾波算法具有很好的初值收斂性，誤差曲線如圖3所示。

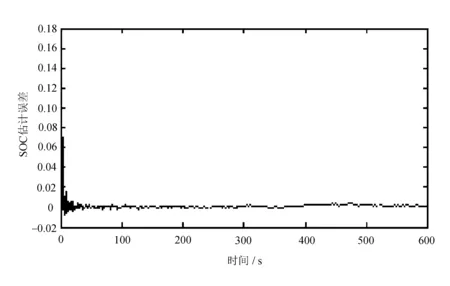
圖3 SOC誤差曲線

5 結(jié) 語

通過安時(shí)計(jì)量法表達(dá)式離散化獲得了磷酸鐵鋰電池組的狀態(tài)方程，引入等效電流系數(shù)和溫度系數(shù)實(shí)現(xiàn)電池容量的修正，建立了電池組的非線性復(fù)合模型，應(yīng)用擴(kuò)展卡爾曼濾波法估計(jì)電池SOC，解決了安時(shí)計(jì)量法不能估算電池初始狀態(tài)和存在累積誤差的問題。仿真實(shí)驗(yàn)表明,該方法能很好地逼近實(shí)驗(yàn)室電池組SOC測(cè)量值，且可行有效。

[1] 詹世安.磷酸鐵鋰電池荷電狀態(tài)估算方法研究[J].電源技術(shù),2015(8):1620-1622.

[2] X Zhang, X Wang, W Zhang, et al. A simplified li-ion battery SOC estimating method[J]. Transaction on Electrical & Electric Materials,2016,17(1):13-17.

[3] 李慧,肖偉,駱萬博.電池剩余電量SOC估計(jì)[J].長春工業(yè)大學(xué)學(xué)報(bào),2017,38(1):73-78.

[4] L Gregory. Plett. Extended Kalman filering for battery management systems of LiPB-based HEV battery packs[J]. Journal of Power Sources,2004,134:252-292.

[5] A Jossen, V Spath, H Doring, et al. Reliable battery operation-a challenge for the battery management systems[J]. Journal of Power Sources,1999,84:283-286.

[6] 張金龍.動(dòng)力電池組SOC估算及均衡控制方法研究[D].天津:天津大學(xué),2011.

[7] 崔立豐,高飛,王永武,等.磷酸鐵鋰動(dòng)力電池Peukert方程修正模型的研究[C]//第六屆中國智能交通年會(huì)暨第七屆國際節(jié)能與新能源汽車創(chuàng)新發(fā)展論壇.2011.

[8] 仝猛,盧蘭光,歐陽明高,等.Peuker方程的適用性分析及基于二階段放電法的Peukert模型修正[J].機(jī)械工程學(xué)報(bào),2010,46(10):121-125.

[9] 齊國光,李建民,郟航,等.電動(dòng)汽車電量計(jì)量技術(shù)的研究[J].清華大學(xué)學(xué)報(bào):自然科學(xué)版,1997,37(3):46-49.

[10] 朱敏.基于電動(dòng)車電池組SOC估計(jì)方法的研究[D].鄭州:河南師范大學(xué),2014.

[11] 何靈娜.基于卡爾曼濾波的動(dòng)力電池SOC估計(jì)算法設(shè)計(jì)[D].杭州:浙江工業(yè)大學(xué),2014.

[12] 徐杰.基于卡爾曼濾波的動(dòng)力電池組SOC精確估計(jì)[D].杭州:杭州電子科技大學(xué),2009.