框架填充墻等效單桿斜撐簡化模型

鄧宏宇，孫柏濤

?

框架填充墻等效單桿斜撐簡化模型

鄧宏宇1, 3，孫柏濤1, 2

(1. 哈爾濱工程大學(xué)航天與建筑工程學(xué)院，黑龍江哈爾濱，150001；2. 中國地震局工程力學(xué)研究所地震工程與工程振動重點實驗室，黑龍江哈爾濱，150080；3. 東北農(nóng)業(yè)大學(xué)水利與土木工程學(xué)院，黑龍江哈爾濱，150030)

在已有的填充墻等效對角斜撐模型的基礎(chǔ)上，結(jié)合近年來地震現(xiàn)場普遍出現(xiàn)的填充墻頂部與框架梁柱節(jié)點接觸處的磚砌體在大震作用下通常會被壓碎這一實際震害現(xiàn)象，改變等效斜撐桿與框架柱的接觸位置，提出一種新的簡化計算模型。通過理論推導(dǎo)給出等效斜撐墻片寬度的計算公式，利用ABAQUS有限元模擬的方法，確定等效斜撐墻片與框架柱合理接觸位置的經(jīng)驗計算公式。最后通過將簡化有限元模型計算結(jié)果與試驗結(jié)果進行對比，驗證該簡化建模方法的正確性。研究結(jié)果表明：傳統(tǒng)的對角斜撐模型低估框架填充墻構(gòu)件的水平承載力，新模型與蘆山地震框架結(jié)構(gòu)震害結(jié)果更相符。本模型可為框架結(jié)構(gòu)抗震分析與設(shè)計驗算提供參考意義。

填充墻；框架結(jié)構(gòu)；等效斜撐模型；抗剪承載力；剛度

鋼筋混凝土框架填充墻結(jié)構(gòu)是我國應(yīng)用最廣泛的結(jié)構(gòu)形式之一，近年來發(fā)生的地震中，由于填充墻與框架梁柱之間相互作用造成的震害十分嚴重[1]。為研究框架填充墻結(jié)構(gòu)的破壞機理，人們常常需要用數(shù)值模擬的方法，建立有限元模型進行分析和計算。因此，研究與框架填充墻構(gòu)件實際受力最為接近的有限元模型的建模方法意義十分重大。在地震工程領(lǐng)域，大致有2類建模方法：一是微觀模型，即采用實體單元精細化模型，這種模型能夠精確的模擬填充墻體的變形、開裂和與框架梁柱的局部應(yīng)力作用，但也存在單元個數(shù)多、計算量大和不容易收斂的問題，無法應(yīng)用于整體模型的大規(guī)模計算。二是宏觀等效模型，即基于一定的假設(shè)，將填充墻簡化為等效斜撐桿來模擬計算。等效斜撐的概念由POLYAJCOV[2]基于試驗提出，他認為填充墻可以簡化為在填充墻對角線方向上只受壓不受拉的斜撐桿。由于等效對角斜撐模型概念簡單、便于應(yīng)用、宏觀上描述了填充墻與框架之間的相互作用，因此在國內(nèi)外有廣泛的應(yīng)用。但該模型也存在一些明顯的不足，該計算模型等效斜撐桿的位置與填充墻對角線方向重合，上部桿端作用在梁柱節(jié)點處，這在彈性階段或者構(gòu)件剛進入彈塑性階段是合理的。但是近年來的震害實際和框架填充墻構(gòu)件的擬靜力推覆試驗表明[3]：在大震作用下，填充墻頂部與梁柱節(jié)點接觸處的角部磚砌體通常會被壓碎從而退出工作，這一破壞形式在地震現(xiàn)場比較普遍[4]。針對大震中框架結(jié)構(gòu)這種較常出現(xiàn)的破壞模式，在極限承載力條件下，仍按等效斜撐桿端支撐在梁柱節(jié)點處來處理是不盡合理的，用該方法建立的模型來模擬結(jié)構(gòu)在彈塑性階段的地震反應(yīng)與地震現(xiàn)場看到的實際的震害不符，因為填充墻體頂部退出工作時墻體實際支撐位置下移，使得框架節(jié)點與支撐位置的部分框架承受很大的剪力，經(jīng)常造成框架根部剪切破壞或節(jié)點破壞。對于等效斜撐模型，最重要的參數(shù)就是確定等效斜撐墻片的有效寬度，國內(nèi)外的研究學(xué)者給出了多種計算方法。其中，HOLMES[5]建議等效斜撐墻片的有效寬度取填充墻對角線長度的1/3；SMITH等[6]通過理論分析引入相對剛度參數(shù)的概念，認為等效墻片寬度與框架和填充墻的剛度比有關(guān)；SANEINEJAD等[7]考慮了結(jié)構(gòu)的非線性，修正了單個等效支撐的面積公式，將等效墻片的有效寬度用與框架梁柱接觸長度的方式來表示；TUCKER[8]通過一系列的框架填充墻構(gòu)件的試驗，對比了18個等效斜撐寬度的計算公式，得出了1個較適合鋼筋混凝土框架砌體填充墻構(gòu)件的等效斜撐寬度公式。由此可見，不同的學(xué)者給出的計算公式差別很大，等效斜撐墻片寬度的取值有待于研究。基于以上的研究現(xiàn)狀，本文作者從實際工程應(yīng)用的角度出發(fā)，在傳統(tǒng)的對角斜撐模型的基礎(chǔ)上，調(diào)整斜撐桿端與框架柱的接觸位置，將斜撐桿上端自梁柱節(jié)點處下移某一距離，提出一種新的等效單桿斜撐模型。結(jié)合理論分析和有限元模擬的方法，給出等效斜撐墻片寬度和等效斜撐桿與框架柱合理的接觸位置的計算公式。該簡化模型適用于大震作用下，在非線性階段，填充墻角部砌體被壓碎這一普遍出現(xiàn)的破壞模式，可應(yīng)用于整體結(jié)構(gòu)大規(guī)模的分析計算。

1 震害實例

1.1 結(jié)構(gòu)破壞情況

2013?04?20T08:02，中國四川省雅安市蘆山縣發(fā)生7.0級地震，震源深度13 km，震中烈度為Ⅸ度。地震造成大量的人員傷亡和房屋建筑破壞。本文作者在第一時間進入雨城區(qū)上里鎮(zhèn)進行震害考察，發(fā)現(xiàn)該地區(qū)鋼筋混凝土框架結(jié)構(gòu)的震害十分嚴重。尤其是教學(xué)樓結(jié)構(gòu)，多采用單跨外廊式的鋼筋混凝土框架結(jié)構(gòu)。圖1所示為蘆山地震雨城區(qū)上里中學(xué)教學(xué)樓震害情況。在地震作用下，框架柱柱頭受剪破壞，填充墻嚴重開裂破壞，填充墻與框架梁柱節(jié)點處的角部磚砌體被壓碎。這種破壞形式在震區(qū)框架結(jié)構(gòu)建筑中十分普遍[9]。為研究框架填充墻構(gòu)件的受力機制和破壞機理，下面用ABAQUS有限元模擬的方法，模擬計算圖1所示的框架填充墻構(gòu)件。

1.2 實體單元模型

首先，通過ABAQUS有限元軟件建立框架填充墻構(gòu)件的實體單元有限元模型。有研究表明，實體單元模型的計算結(jié)果與實際構(gòu)件最為接近[10]。為驗證實體單元計算結(jié)果的準確性，根據(jù)MEHRABI等[11]所做的一系列框架填充墻構(gòu)件模型擬靜力試驗，模擬其中的構(gòu)件1、構(gòu)件8和構(gòu)件9，并將有限元計算結(jié)果與通過試驗所得實際數(shù)據(jù)進行對比。其中構(gòu)件1為空框架，構(gòu)件8為空心砌塊填充墻，構(gòu)件9為實心磚填充墻，相關(guān)的試件尺寸和材料參數(shù)見文獻[11]。

ABAQUS中建模過程如下：框架梁柱采用實體單元C3D20R，鋼筋采用桁架單元T3D2，本構(gòu)關(guān)系選擇對應(yīng)的混凝土和鋼筋塑性本構(gòu)[12]，填充墻采用實體單元C3D20R，本構(gòu)關(guān)系采用砌體塑性本構(gòu)[13]，將材料的本構(gòu)關(guān)系賦予到ABSQUS中的混凝土損傷塑性模型進行彈塑性的靜力模擬分析。鋼筋與混凝土框架梁柱之間采用embedded連接，填充墻與框架梁柱之間采用contact連接模擬填充墻與框架梁柱之間的相互作用。采用隱式靜力分析的方法，在梁端施加側(cè)向荷載，最終能夠得到1條荷載?位移曲線見圖2。

(a) 框架填充墻破壞；(b) 填充墻角部被壓碎

從圖2中試件荷載?位移曲線的試驗值與各自對應(yīng)的實體單元有限元模擬值的對比可以看出：2條曲線的最大水平承載力值比較吻合，驗證了采用實體單元有限元模型靜力分析得到的構(gòu)件的最大水平承載力模擬結(jié)果與實際相符。因此，在后續(xù)的分析過程中，認為實體單元模型的計算結(jié)果即為構(gòu)件的實際值。

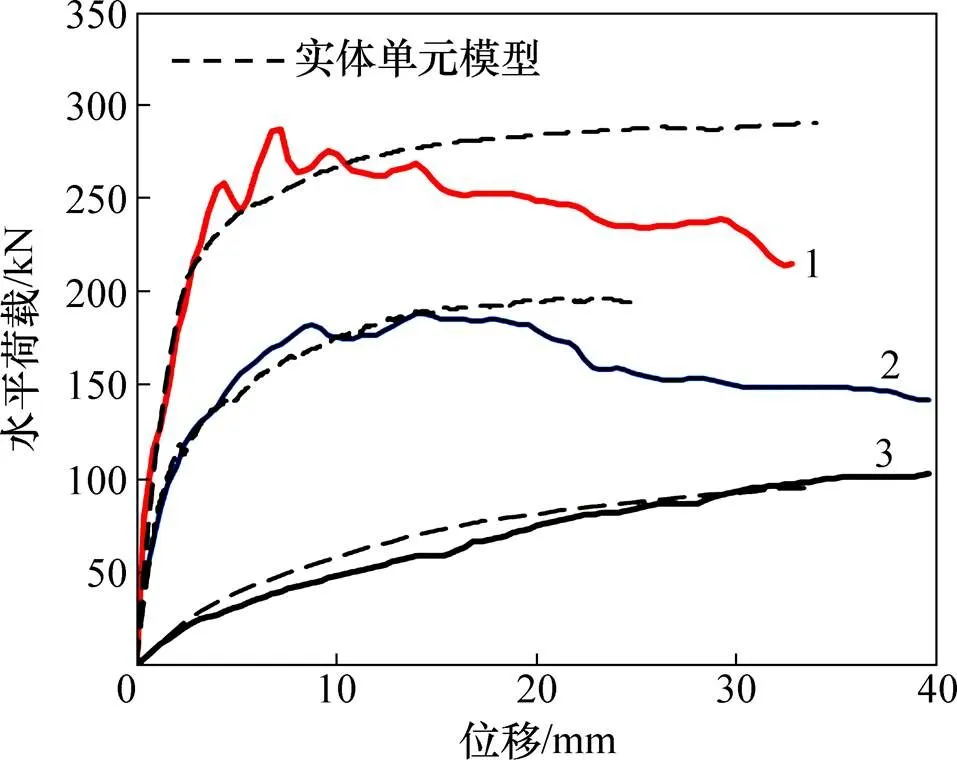
1—實心磚填充墻；2—空心砌塊填充墻；3—空框架。

1.3 震害實例計算結(jié)果

將圖1中的框架填充墻構(gòu)件單獨提取出來，采用已驗證的實體單元有限元建模方法對其進行模擬計算分析，并將計算結(jié)果與實際結(jié)果進行對比。圖3所示為構(gòu)件達到極限水平承載力后某一時刻的Mises應(yīng)力云圖。

從圖3(a)可以看出：隨著框架填充墻構(gòu)件側(cè)向變形的增加，填充墻右上角的磚砌體受到框架梁柱節(jié)點的擠壓，當(dāng)超過砌體材料的極限變形能力時，磚砌體就會因為壓碎而退出工作。從填充墻的Mises應(yīng)力云圖可以看出填充墻中應(yīng)力的分布和變化趨勢，在初始階段，填充墻右上角的角部磚砌體應(yīng)力最大，對角斜撐的作用比較明顯。當(dāng)位移進一步增大時，角部的最大應(yīng)力會有一定程度的下移(圖3(b))，此時對角斜撐模型不再適用。圖3(c)中，從框架柱與填充墻接觸面的壓應(yīng)力變化也可以看出，最大應(yīng)力的位置隨著框架側(cè)向位移的增大而逐漸下移。以上計算結(jié)果最終狀態(tài)與實際震害比較相符，說明高烈度區(qū)的結(jié)構(gòu)遭到大震作用時，填充墻對框架的對角斜撐位置有一定的下移，原來始終保持在對角線方向上的對角斜撐模型不盡合理，應(yīng)對模型進行改進和調(diào)整，才能更好地適用非線性階段的模擬分析。

(a) 整體Mises應(yīng)力云圖；(b) 填充墻Mises應(yīng)力云圖；(c) 接觸面處壓應(yīng)力變化

基于以上的實際震害和有限元模擬的初步分析，提出一種適用于普遍出現(xiàn)的填充墻角部砌體被壓碎的受力模型，根據(jù)該模型，從受力分析的角度，推導(dǎo)出等效斜撐墻片寬度的計算公式，并通過設(shè)計一系列構(gòu)件對其計算結(jié)果進行統(tǒng)計回歸，給出等效斜撐桿與框架柱接觸位置的經(jīng)驗計算公式。

2 等效斜撐墻片寬度

2.1 計算簡圖和基本假設(shè)

單榀框架填充墻構(gòu)件的計算簡圖如圖4所示，在地震荷載作用下，認為只有一定寬度的斜撐墻片參與受力，其與框架柱的接觸長度為c，墻片厚度與填充墻厚度相同，等效斜撐墻片的中軸線與水平方向的夾角為′。針對該模型，做出如下基本假設(shè)：1) 普通磚砌體填充墻為各向同性的理想勻質(zhì)材料。2) 在以下的受力分析中，為簡便起見假設(shè)填充墻的邊界與框架梁柱的中軸線一致，即′≈，′≈，其中′和′為框架軸線處的高度和跨度，和為填充墻的高度和跨度。3) 簡化的斜撐填充墻頂部在構(gòu)件進入極限承載力，角部磚砌體被壓碎之后認為與梁沒有接觸，此時斜撐墻片的頂端與框架梁之間存在一定的距離，且與柱的接觸長度不超過0.3倍填充墻高，見式(1)。4) 框架柱、框架梁內(nèi)最大彈性彎矩與屈服彎矩的比值不超過0.2[14]。見下式：

c≤0.3(1)

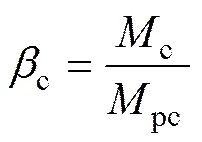
≤(2)

式中：c為等效斜撐墻片與框架柱的接觸長度與框架柱高度的比值；為填充墻的高度；c和b為框架柱、框架梁的最大彈性彎矩；pc和pb分別為框架柱、框架梁的屈服彎矩；c和b分別為框架柱、框架梁內(nèi)彈性彎矩與屈服彎矩的比值；0為框架柱、框架梁內(nèi)彈性彎矩與屈服彎矩的比值最大值。

圖4 框架填充墻構(gòu)件在角部磚砌體被壓碎后的計算簡圖及受力

2.2 理論公式推導(dǎo)

等效接觸面長度指的是等效斜撐墻片與框架柱的接觸長度。這里等效斜撐墻片的寬度以等效接觸面長度的形式給出。在極限水平承載力作用下，等效斜撐墻片在與框架柱接觸面處受剪、受壓綜合作用而導(dǎo)致破壞。根據(jù)特雷斯卡(Tresca)六棱柱體屈服準則[14]得：

(4)

式中：為填充墻等效斜撐墻片與框架柱之間均布正應(yīng)力；為填充墻等效斜撐墻片與框架柱之間均布剪應(yīng)力；為框架梁柱的高跨比，即=′/′；為等效斜撐填充墻與框架柱之間的摩擦因數(shù)，一般取0.45[16]。聯(lián)立式(3)和式(4)，得出接觸面均布正應(yīng)力為

式中：c0為填充墻與框架柱之間名義均布正應(yīng)力，c為填充墻材料的有效抗壓強度，可按計算；為填充墻材料的抗壓強度；為調(diào)整系數(shù)，可取[16]。

圖5所示為框架填充墻受力變形圖。由圖5可見：在水平荷載作用下，假設(shè)等效斜撐填充墻片與框架柱分離的點為，為簡化分析，在接觸長度范圍內(nèi)均布剪應(yīng)力忽略不計，將柱段單獨提取出來作為分離體進行受力分析，根據(jù)彎矩平衡得

式中：c為框架柱彈性彎矩；pj為節(jié)點塑性抵抗彎矩，取節(jié)點處框架梁、柱的屈服彎矩及節(jié)點屈服彎矩的最小值。將式(2)代入式(6)，并結(jié)合式(1)，求解出等效接觸面長度c為

(7)

通過以上的推導(dǎo)，將等效斜撐墻片寬度以斜撐墻片與框架柱接觸長度c的形式給出。當(dāng)1個框架填充墻構(gòu)件的尺寸、材料等級確定之后，除之外的其余參數(shù)就都已經(jīng)確定。即等效斜撐墻片自梁柱節(jié)點處下移的距離，不僅是等效斜撐墻片寬度計算公式的必要參數(shù)之一，也是將實體單元模型簡化為單桿斜撐模型，從而可以應(yīng)用于整體結(jié)構(gòu)大規(guī)模的分析計算的關(guān)鍵。以下介紹經(jīng)驗計算公式的確定過程和簡化模型的建模方法。

(a) 整體框架變形示意圖；(b) 柱EA段受力分析圖

3 斜撐桿與框架柱的接觸位置

3.1 構(gòu)件設(shè)計

設(shè)計一系列層高′和跨度′不同，跨高比相同的框架填充墻構(gòu)件。其中框架梁、柱的截面尺寸和配筋相同，框架柱截面尺寸(長×寬)為350 mm×350 mm，框架梁截面尺寸(長×寬)為500 mm×250 mm，混凝土強度等級取C30，保護層厚度取35 mm，縱向受力鋼筋采用直徑為16 mm的HRB335鋼筋，箍筋采用直徑為8 mm的HPB235鋼筋，填充墻砌體強度等級為MU10/M5，填充墻厚度取120 mm，框架的抗震等級為3級，設(shè)計軸壓比取0.2，跨高比均為1.5。具體設(shè)計參數(shù)見表1。

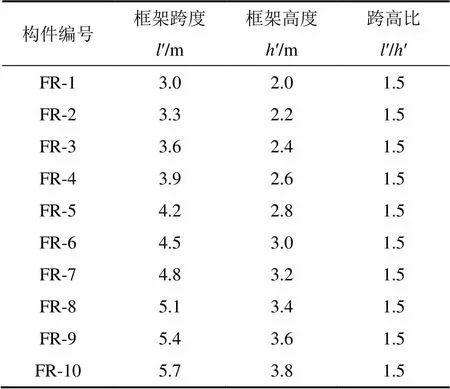
表1 構(gòu)件設(shè)計參數(shù)

3.2的確定

首先采用實體單元模型的建模方法，在ABAQUS中對表1中的各個構(gòu)件進行模擬計算。然后在實體單元有限元模型的基礎(chǔ)上，采用桁架單元T3D2，將實體單元的填充墻替換為等效斜撐桿。桿兩端與框架之間采用join連接，即節(jié)點之間允許有相對轉(zhuǎn)角，但不允許有相對位移，對應(yīng)于框架梁柱和填充墻之間只傳遞剪力，不傳遞彎矩的情況；材料屬性與填充墻使用的砌體本構(gòu)關(guān)系一樣，在設(shè)置材料屬性時規(guī)定只承受壓力不能承受拉力。簡化模型情況如圖6所示。

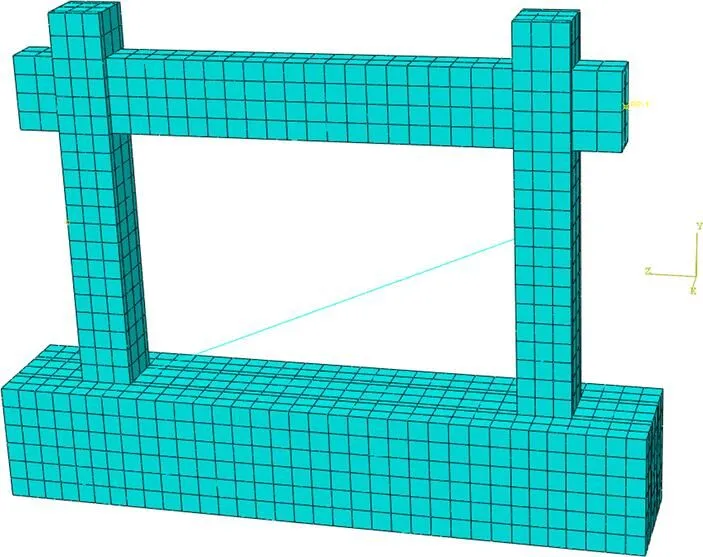
圖6 等效單桿斜撐模型

逐漸調(diào)整的取值即變化等效斜撐墻片與框架柱的接觸位置，直至等效單桿斜撐模型的荷載?位移曲線與實體單元有限元模型的荷載?位移曲線相吻合，記錄此時的，認為此時的值即為該構(gòu)件的合理取值。各個構(gòu)件框架梁和框架柱的屈服彎矩按下式計算：

(9)

從圖7可以看出：當(dāng)3=350 mm時，簡化斜撐模型與實體單元模型計算的荷載?位移曲線在平臺段最為符合，因此認為對于構(gòu)件FR-1，的合理取值為350 mm。按照上述方法，對其余9個構(gòu)件采用同樣的分析過程，找出當(dāng)?shù)刃螚U斜撐模型的荷載?位移曲線的水平承載力最大值與實體單元有限元模型的計算結(jié)果相符時的取值。

3.3 經(jīng)驗公式擬合

通過式(7)的推導(dǎo)看出, 等效壓桿的有效寬度可以通過含的表達式來表示，兩者之間成正比例關(guān)系。有研究認為，等效壓桿的有效寬度與′cos′和′有關(guān)[17]。再結(jié)合觀察有限元實體單元模型的分析結(jié)果，本文認為與′cos′有關(guān)，/′cos′可以寫成含有′的函數(shù)表達式。其中，為相對剛度參數(shù)，是由SMITH等[6]提出的，其計算公式為

式中：m為填充墻材料的彈性模量；c為混凝土的彈性模量；為填充墻厚度；為填充墻對角線與水平方向的夾角；c為框架柱的截面慣性矩；為填充墻的高度。

本文認為/(′cos′)和′之間存在函數(shù)關(guān)系，分別計算上述設(shè)計的10個構(gòu)件中當(dāng)取合適的值時對應(yīng)的/(′cos′)和′，將/(′cos′)作為縱坐標，′作為橫坐標，并放在同一直角坐標系下，得到一系列的分布點，如圖8所示。

對以上這些分布點擬合曲線得到的經(jīng)驗計算式為

通過式(11)可以計算，即等效斜撐墻片自框架梁柱節(jié)點下移的距離。當(dāng)1個框架填充墻構(gòu)件的截面尺寸和材料等級確定后，可通過式(11)和式(7)計算出等效斜撐桿與框架柱的接觸位置和等效斜撐墻片的寬度，即可建立對應(yīng)的等效簡化有限元模型。

1—實體單元模型；2—斜撐墻片下降1=150 mm；3—斜撐墻片下降2=250 mm；4—斜撐墻片下降3=350 mm；5—斜撐墻片下降4=450 mm；6—斜撐墻片下降5=550 mm。

圖7 構(gòu)件FR-1荷載?位移曲線

Fig. 7 Load?displacement curve of member FR-1

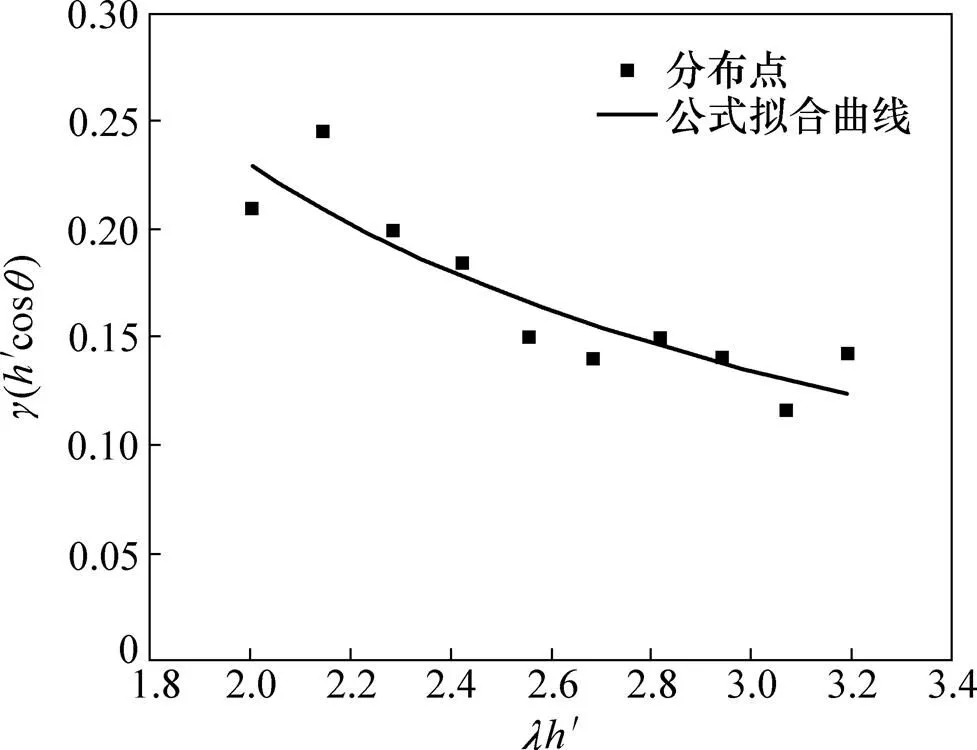
圖8 分布點和公式擬合曲線

4 實例應(yīng)用

4.1 試驗及相關(guān)數(shù)據(jù)

Shine和Mehrabi為研究填充墻對框架性能的影響，進行了一系列共12個框架填充墻構(gòu)件的擬靜力試驗。本文對其中的構(gòu)件8和構(gòu)件9進行模擬驗證。構(gòu)件8的填充墻為混凝土空心砌塊，構(gòu)件9的填充墻為實心磚砌體，構(gòu)件尺寸、材料參數(shù)和實驗情況詳見文獻[11]。

4.2 有限元計算與實驗結(jié)果對比

對以上2個構(gòu)件，分別采用實體單元接觸連接模型、本文提出的改進的等效簡化斜撐模型和傳統(tǒng)的對角斜撐模型進行有限元模擬。其中，傳統(tǒng)的對角斜撐簡化模型的等效墻片寬度的取值采用TUCKER[8]提出的計算公式：

式中：為等效斜撐的寬度；′為填充墻對角線的長度；′為框架的高度；為相對剛度參數(shù)。TUCKER[8]提出的等效斜撐寬度的計算公式在對角斜撐模型中應(yīng)用最為廣泛，具有較普遍的意義[18]。構(gòu)件8、構(gòu)件9的3種有限元建模方法計算結(jié)果與實驗結(jié)果的比較見圖9。

從圖9可以看出：采用本文所述的簡化建模方法所得到的框架填充墻構(gòu)件的最大水平承載力與試驗所得數(shù)據(jù)和采用實體單元接觸連接模型的計算結(jié)果三者之間比較吻合，驗證了該等效簡化模型的合理性和準確性。對于傳統(tǒng)的對角斜撐模型，始終保持在對角線方向上的對角斜撐模型不盡合理，等效墻片寬度采用TUCKER[8]公式所得的最大水平承載力低于上述3種結(jié)果，說明該對角斜撐模型低估了框架填充墻構(gòu)件的最大水平承載力，與構(gòu)件的實際受力誤差較大。

(a) 構(gòu)件8；(b) 構(gòu)件9

5 結(jié)論

1) 在等效對角斜撐桿模型的基礎(chǔ)上，結(jié)合震害實例中填充墻頂部與框架梁柱節(jié)點接觸處的磚砌體在大震作用下通常會被壓碎的情況，將等效斜撐桿與框架柱的接觸位置下移一定的距離，提出一種新的簡化計算模型。在該模型的基礎(chǔ)上進行受力分析和理論公式推導(dǎo)，給出了等效斜撐墻片寬度的計算公式。等效斜撐桿與框架柱接觸位置的經(jīng)驗計算公式則是通過設(shè)計一系列框架填充墻構(gòu)件進行有限元模擬，并對結(jié)果進行統(tǒng)計回歸的方法得到。由此可以建立一種改進的等效單桿斜撐簡化模型，與震害實際更相符。

2) 實體單元模型可以很好的模擬框架填充墻構(gòu)件的受力情況，但計算單元多，計算時間長且不容易收斂。按本文所介紹的等效簡化模型的數(shù)值模擬結(jié)果與實體單元模型計算結(jié)果和實驗所得實測數(shù)據(jù)三者之間吻合得很好，采用等效簡化模型不僅大大節(jié)省了計算成本，同時也使得帶填充墻的框架結(jié)構(gòu)整體模型的大規(guī)模時程分析計算成為可能。

3) 該簡化計算模型存在一定的局限性，即只適用于在大震作用下，填充墻角部磚砌體被壓碎這一破壞模式的模擬計算。在彈性階段，填充墻與框架梁柱之間的傳力方向是按對角線方向傳遞的，此時采用已有的對角斜撐模型即可。只有在構(gòu)件進入非線性后，框架填充墻構(gòu)件才會普遍出現(xiàn)填充墻與框架柱接觸處最大應(yīng)力區(qū)域下移的情況。對于處于高烈度區(qū)、嚴重破壞且符合本文所述的破壞模式的框架填充墻結(jié)構(gòu)，采用本文所介紹的簡化有限元模型進行分析更符合震害實際，模擬結(jié)果也更準確。

[1] 葉列平, 曲哲, 馬千里, 等. 從汶川地震框架結(jié)構(gòu)震害談“強柱弱梁”屈服機制的實現(xiàn)[J]. 建筑結(jié)構(gòu), 2008, 38(11): 52?67. YE Lieping, QU Zhe, MA Qianli, et al. Study on ensuring the strong column?weak beam mechanism for RC frames based on the damage analysis in the Wenchuan earthquake[J]. Building Structure, 2008, 38(11): 52?67.

[2] POLYAJCOV S V. On the interactions between masonry filler walls and enclosing frame when loaded in the plane of the wall[J]. Translations in Earthquake Engineering Research Institute, 1956, 32(2): 1?25.

[3] 金煥.填充墻RC框架結(jié)構(gòu)地震破壞機理及關(guān)鍵抗震措施研究[D]. 哈爾濱: 中國地震局工程力學(xué)研究所, 2014: 35?47. JIN Huan. Research on seismic failure mechanisms and key aseismic measures for masonry-infilled RC frame structures[D]. Harbin: Institute of Engineering Mechanics, 2014: 35?47.

[4] SUN Baitao, YAN Peilei, CHEN Xiangzhao. New characteristics of intensity assessment of Sichuan Lushan“4.20”Ms7.0 earthquake[J]. Earthquake Engineering and Engineering Vibration, 2014, S1(13): 123?139.

[5] HOLMES M. Combined loading on infilled frames[J]. Proceedings of the Institution of Civil Engineers, 1963, 25(5): 31?38.

[6] SMITH B S, CARTER C. A method of analysis for infilled frames[J]. Proceedings Institution of Civil Engineers, 1969, 44(1): 31?48.

[7] SANEINEJAD A, HOBBS B. Inelastic design of infilled frames[J]. Journal of Structural Engineering, 1995, 121(4): 634?650.

[8] TUCKER C J. Predicting the in-plane capacity of masonry infilled frames[D]. USA: The University of Tennessee. College of Civil Engineering, 2007: 57?69.

[9] 孫柏濤, 閻培雷, 王明振, 等. 四川省蘆山“4.20”7.0級強烈地震建筑物震害圖集[M]. 北京: 地震出版社, 2014: 11?13. SUN Baitao, YAN Peilei, WANG Mingzhen, et al. Earthquake damage atlas of Sichuan Lushan“4.20”Ms7.0 earthquake[M]. Beijing: Earthquake Publishing House, 2014: 11?13.

[10] KOUTROMANOS I, STAVRIDIS A, SHING P B, et al. Numerical modeling of masonry-infilled RC frames subjected to seismic loads[J]. Computers and Structures, 2011, 89(1): 1026?1037.

[11] MEHRABI A B, SHING P B, SCHULLER M P, et al. Experimental evaluation of masonry-infilled RC frames[J]. Journal of Structural Engineering, 1996, 122(3): 228?237.

[12] GB 50010—2010, 混凝土結(jié)構(gòu)設(shè)計規(guī)范[S]. GB 50010—2010, Code for design of concrete structures[S].

[13] 劉桂秋. 砌體結(jié)構(gòu)基本受力性能的研究[D]. 長沙: 湖南大學(xué)土木工程學(xué)院, 2005: 21?25. LIU Guiqiu. The research on the basic mechanical behavior of masonry structure[D]. Changsha: Hunan University. College of Civil Engineering, 2005: 21?25.

[14] ACI 318M—05, Building code requirements for structural concrete[S].

[15] CHEN W F. Plasticity in reinforced concrete[M]. New York：McGraw-Hill Book Co, 1982: 29?38.

[16] ACI530—02, Building code requirements for masonry structures[S].

[17] 金曉飛, 高松召, 楊曉杰, 等. 內(nèi)嵌墻板鋼框架等效單斜撐簡化模型[J]. 哈爾濱工業(yè)大學(xué)學(xué)報, 2013, 45(6): 16?21. JIN Xiaofei, GAO Songzhao, YANG Xiaojie, et al. Equivalent single strut simplified model for steel frames with embedded retaining wall[J]. Journal of Harbin institute of technology, 2013, 45(6): 16?21.

[18] 閻紅霞. 樓板和填充墻對RC框架結(jié)構(gòu)抗震性能的影響[D]. 北京: 北京交通大學(xué), 2012: 121?133. YAN Hongxia. Influences of slabs and infill walls on seismic performance of reinforced concrete frame structures[D]. Beijing: Beijin Jiaotong University, 2012: 121?133.

(編輯 陳愛華)

Equivalent diagonal bracing model of a frame-filled wall

DENG Hongyu1, SUN Baitao1, 2

(1. College of Space Technology and Civil Engineering, Harbin Engineering University, Harbin 150001, China;2. Key Laboratory of Earthquake Engineering and Engineering Vibration,Institute of Engineering Mechanics, China Earthquake Administration, Harbin 150080, China;3. School of Water Conservancy and Civil Engineering, Northeast Agricultural University, Harbin 150030, China)

Based on the existing equivalent diagonal strut model, combined with the actual earthquake damage phenomena that the brick masonry between the top of the infill wall and the beam-column connections is often crushed during a strong earthquake, and changing the contact position between the equivalent bracing wall and column, a new calculation model was generated. Through theoretical derivation, the formulae for calculating the contact length between the equivalent bracing wall and column was given. Using the ABAQUS finite element simulation, an empirical formula for the reasonable contact position between the equivalent bracing wall and column was determined. Finally through comparing the finite element model calculation results with the experimental result, the validity of the simplified modeling method was verified. The results show that the traditional diagonal strut model underestimates the horizontal bearing capacity of the infill-frame, and the new model is more consistent with the seismic damage of frame structure in Lushan earthquake. The model has reference significance to seismic analysis of frame structure.

masonry infill panel; reinforced concrete frame structure; equivalent strut mode; shear strength; stiffness

10.11817/j.issn.1672?7207.2017.02.023

TU31

A

1672?7207(2017)02?0440?08

2016?03?15；

2016?06?10

國家自然科學(xué)基金資助項目(91315301)；地震行業(yè)科研專項(201508026-01，201508010-06)(Project(91315301) supported by the National Natural Science Foundation of China; Projects(201508026-01, 201508010-06) supported by Earthquake Industry Research)

鄧宏宇，博士，講師，從事結(jié)構(gòu)抗震研究；E-mail：dengblue@163.com