蝴蝶定理在仿射幾何中的推廣

黃一德，田秀蓉

（華南農業大學 數學與信息學院，廣東 廣州 510642）

蝴蝶定理在仿射幾何中的推廣

黃一德，田秀蓉

（華南農業大學 數學與信息學院，廣東 廣州 510642）

歷史上關于蝴蝶定理的各種推廣和證明,紛繁復雜.本文試圖整理出蝴蝶定理在保留中點的情況下,在仿射幾何中最好的推廣方式,并給出綜合法的證明.本文得到的主要結果是定理1,2,3,這三條定理可以包擴蝴蝶定理在仿射幾何領域的各種推廣.最后通過定理4驗證了上述結果.

蝴蝶定理；Desargues第2定理；仿射幾何

1 引言

蝴蝶定理自從1803年被提出,直到現在依然可以看到有關蝴蝶定理的論文發表.例如從1986年到2016年,國內的期刊上主題是關于蝴蝶定理的論文,我們找到的就有110篇,而出現的有關證明也是數不勝數.真有點讓人不知要領.《大學》說：“止于至善.”那么蝴蝶定理的至善推廣和證明應該是什么呢?本文試圖整理出蝴蝶定理在保留中點的情況下,在仿射幾何中最好推廣方式,并給出綜合法的證明.

2 歐氏幾何中的蝴蝶定理

蝴蝶定理最早提出的時候是一個歐氏幾何定理,可以敘述如下.

蝴蝶定理經過一個圓的弦CC'的中點A作另外兩條弦ST和UV.直線CC'分別交直線SU,TV于點B,B'.那么A是B,B'的中點[1].

如果需要在蝴蝶定理中保留中點這個概念,那么在歐氏幾何中,應該沒必要再討論蝴蝶定理的各種推廣了,也沒有必要在歐氏幾何中找蝴蝶定理的最反映問題本質的證明,因為把蝴蝶定理的圓改為橢圓,雙曲線或拋物線,定理依然成立,而且證明并不需要涉及度量概念 (距離,角度等).例如1892年,John Casey用交比證明了蝴蝶定理[1].但如果不保留中點這個概念,蝴蝶定理還是有一些有意義的推廣的,例如A.Kandy的推廣[1].

3 蝴蝶定理在仿射幾何中的推廣

因為中點是一個仿射不變量,所以如果需要在蝴蝶定理中保留中點這個概念,我們應該在仿射幾何中推廣蝴蝶定理.本文的仿射幾何指的是實仿射幾何.我們知道,常常可以借助射影幾何研究仿射幾何,我們研究蝴蝶定理的工具就是Desargues第二定理.

Desargues第二定理設直線l與一個二階曲線束S相交,且l不過S的任一基點,則與S的每一條二階曲線的一對交點都屬于同一個對合[2].

按照基點為4個,退化為3個和退化為2個,可以把Desargues第二定理分別敘述為三個定理, 見[3]第五章定理19,20,21.

為了在仿射幾何中推廣蝴蝶定理并給出綜合法的證明,我們先證明一個引理.

引理設l是一條平常直線,N是l上的無窮遠點,σ是l上點列的一個對合.

(1)如果無窮遠點N是σ的一個二重點,那么σ在上的限制是關于另一個二重點M的反射.

(2)如果σ有兩個相異的平常的共軛點對,它們有相同的中點M,那么σ在l-{N}上的限制是關于點M的反射.

說明如果一個對合有一個二重元素,那么它有另一個不同于前者的二重元素([3]第四章定理27推論4).

證明(1)設A,A'是σ的一對平常的共軛點,那么它們與M,N構成調和共軛點對([3]第四章定理27推論1).因為N是無窮遠點,所以M是A,A'的中點.因此σ在l-{N}上的限制是關于點M的反射.

(2)設A,A'和B,B'是兩個相異的平常的共軛點對,它們有相同的中點M.令σ'是一個l上點列的對合,使得M和N是二重點(σ'是存在的,見[3]第四章定理27推論2).根據(1), σ'在l-{N}上的限制是關于點M的反射.因為σ和σ'在A,B上的作用相同,所以([3]第四章定理26推論).證畢.

定理1(仿射幾何中的蝴蝶定理) 令S,T,U,V是四個平常點,其中任意三點不共線.設三條互異的二階曲線經過這四個公共點.又令不經過這四個點的一條平常直線l與這三條二階曲線的三對交點分別是A,A',B,B',C,C'.于是如果有一對交點的兩個點都是直線l上的無窮遠點,那么另外兩對交點有相同中點.如果三對交點的點都是平常點,并且其中兩對交點有相同中點,那么這個點也是另外一對交點的中點.

說明(1)顯然,三對交點的集合{A,A'},{B,B'},{C,C'}互不相交.

(2)l與一條非退化二階曲線的兩個交點重合,相當于說l與這條非退化二階曲線相切于這個交點.

(3)如果三對交點都是平常點,并且其中一對交點重合,例如,如果A=A',那么定理的結論就相當于說,A是B,B'的中點等價于A是C,C'的中點.

(4)如果定理1所說的一條二階曲線是退化的,那么它是完全四點形STUV的一對對邊.

(5)如果定理1所說的一條二階曲線與l的兩個交點都是無窮遠點,那么或者這條二階曲線是完全四點形STUV的一對對邊,并且這對對邊平行于l,或者這條二階曲線是雙曲線,它的一條漸近線是l.

圖1畫的是這三條二階曲線有兩條退化,一條非退化時的示意圖.

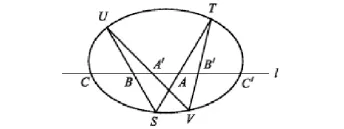
圖1

證明根據[3]第五章定理19,這三對交點是同一個對合的三對共軛點.如果A,A'都是直線l上的無窮遠點,那么B,B',C,C;都是直線l上的平常點,根據引理的(1),B,B'的中點與C,C'的中點相同.如果三對交點的點都是平常點,并且A, A'與B,B'有相同的中點,那么根據引理的(2),這個點也是C, C'的中點.證畢.

定理1中的四個點可以退化為三個點,這時定理按如下方式理解.

定理2(定理1的退化情形1)令T,U,V是不共線三個平常點,t是經過點T但不經過U,V的直線.設三條互異的二階曲線屬于下列情形：與直線相切于T,并經過U和V的非退化二階曲線,或直線對t,UV,或直線對TU,TV.又令不經過T,U,V的一條平常直線l與這三條二階曲線的三對交點分別是A,A',B,B',C,C'.于是如果有一對交點的兩個點都是直線l上的無窮遠點,那么另外兩對交點有相同中點.如果三對交點的點都是平常點,并且其中兩對交點有相同中點,那么這個點也是另外一對交點的中點.

說明如果定理2所說的一條二階曲線與l的兩個交點都是無窮遠點,那么或者這條二階曲線是直線對t,UV,并且t,UV平行于,或者這條二階曲線是雙曲線,它的一條漸近線是l.

圖2畫的是這三條二階曲線有兩條退化,一條非退化時的示意圖.

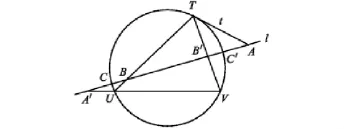
圖2

證明根據[3]第五章定理20,這三對交點是同一個對合的三對共軛點.證明的其余部分可參考定理1的證明.證畢.

定理1中的四個點還可以退化為兩個點,這時定理按如下方式理解.

定理3(定理1的退化情形2)令T,V是兩個不同的平常點,t是經過T但不經過V的直線,v是經過V但不經過T的直線.設三條互異的二階曲線屬于下列情形：t與直線v和 分別相切于點T和V的非退化二階曲線,或直線對t,v,或重合直線對TV.又令不經過T,V的一條平常直線l與這三條二階曲線的三對交點分別是A,A',B,B',C,C'.于是如果有一對交點的兩個點都是直線l上的無窮遠點,那么另外兩對交點有相同中點.如果三對交點的點都是平常點,并且其中兩對交點有相同中點,那么這個點也是另外一對交點的中點.

說明如果定理3所說的一條二階曲線與l的兩個交點都是無窮遠點,那么或者這條二階曲線是直線對s,t,并且s,t平行于l,或者這條二階曲線是重合直線對ST,并且ST平行于 ,或者這條二階曲線是雙曲線,它的一條漸近線是.

圖3畫的是這三條二階曲線有兩條退化,一條非退化時的示意圖.

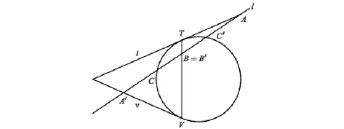
圖3

證明根據[3]第五章定理21,這三對交點是同一個對合的三對共軛點.證明的其余部分可參考定理1的證明.證畢.

定理1,2,3可以包擴蝴蝶定理在仿射幾何的各種推廣.

4 應用舉例

根據定理1,2,3,在仿射平面上很容易得出不少蝴蝶定理的特例.我們舉一個稍微復雜一點的例子.

定理4設CC'DD'是平常的簡單四點形,S,T,U,V分別是直線CD,C'D',CD',C'D上的平常點,其中任意三點不共線, {C'C'D'D'}和{S,T,U,V}不相交,并且四條直線CC',DD',ST,UV相交于點A.又令直線CC'與直線SU,TV的交點分別是B, B'.于是A是B,B'的中點等價于A是C,C'的中點.

證明顯然CSTC'VU是一個簡單六點形,它的三對對邊的交點分別是D,A,D',而這三個點在一直線上,根據Pascal定理的逆定理,六點形CSTC'VU內接于一條二階曲線.于是直線CC'與這條二階曲線以及直線對ST,UV,直線對SU,TV的三對交點分別是C,C',A,A,B,B'.根據定理1,A是B,B'的中點等價于A是C,C'的中點.證畢.

在定理4中,如果把簡單四點形CC'DD'改為箏形,那么定理4就變為1990年全國數學冬令營競賽的一道試題.這樣一改,定理4就從仿射幾何問題變為歐氏幾何問題,因為箏形是歐氏幾何的概念.

〔1〕L.Bankoff.The Metamorphosis of the Butterfly Problem[J].Mathematics Magazine,1987,60(4)：195-210.

〔2〕鐘集.高等幾何[M].北京：高等教育出版社,1983.3.

〔3〕O.VeblenandJ.W.Young.Projective Geometry, Volume 1[M].Charleston：Biblio Bazaar,2009.

O185

A

1673-260X（2017）02-0004-02

2016-10-27